(X，I)-Gorenstein內射模的可解性及等價刻畫

何東林，李煜彥

(隴南師范高等專科學校數信學院，甘肅隴南742500)

Gorenstein同調理論是同調代數理論的研究熱點之一。Holm[1]提出并研究了Gorenstein同調維數，Pan[2]等將其推廣到(X，Y)-Gorenstein投射模與內射模，本文主要討論(X，I)-Gorenstein內射模的可解性及其若干等價刻畫。

本文中的環均指有單位元的結合環，模指左R-模，P表示投射左R-模類，I表示內射左R-模類。X,Y均為左R-模類，且I?X，P ?Y。HomR(X,-)表示所有函子HomR(X,-)組成的類，其中X∈X。先給出兩個基本概念。

定義1[1]稱模類X是內射可解的，如果I?X，且對任意短正合列

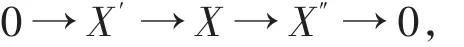
其中X′∈X，有X∈X與X″∈X等價。

定義2[2]稱模M是(X，Y)-Gorenstein內射模，如果存在HomR(X,-)下正合的正合列其中M ?Coker(Y1→Y0)且Yi,Yi?Y。

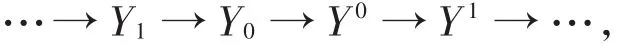
引理1如果模類Y關于直積封閉，那么(X，Y)-Gorenstein內射模也關于直積封閉。

特別地，當Y=I時，用(X，I)-GI表示所有(X，I)-Gorenstein內射模組成的類。顯然內射模一定是(X，I)-Gorenstein內射模。下面給出本文的主要結論。

定理1設N是左R-模，則以下條件等價

(1)N是(X，I)-GI模；

(2)Exti≥1R(X,N)=0(對任意 X ∈X)，且存在HomR(X，-)下正合的正合列

…→I2→I1→I0→N→0，

其中Ii∈I(i=0,1,2,…)；

(3)存在短正合列0→K→I→N→0，其中I∈I且K ∈(X，I)-GI。

證明 由定義易知(1)?(2)?(3)顯然成立。下面只需證(3)?(2)成立即可。

因為在短正合列0→K→I→N→0中K∈(X，I)-GI，所以對任意i≥1及任意X ∈X，有Exti

R(X,K)=0且存在HomR(X，-)下正合的正合列

其中Ii∈ I(i=0,1,2,…)。用函子HomR(X，-)作用于短正合列0→K→I→N→0可得如下長正合列

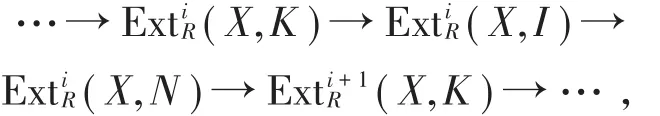
又由I∈I知

結合正合列…→I2→I1→I0→K→0及0→K→I→N→0易得HomR(X，-)下正合的正合列…→I2→I1→I0→I→N→0。

定理2 模類(X，I)-GI是內射可解的。

證明 設0→M→N→Q→0是左R-模短正合列，其中M ∈(X，I)-GI。若Q ∈(X，I)-GI，因為內射模類I關于直積封閉，由引理知模類Q∈(X，I)-GI也關于直積封閉。根據文獻[1]中引理1.7可得，模類(X，I)-GI關于擴張封閉，從而N ∈(X，I)-GI。若N ∈(X，I)-GI，則由定理1知存在短正合列0→K→I→N→0，其中I∈I且K∈(X，I)-GI。考慮如下拉回圖：

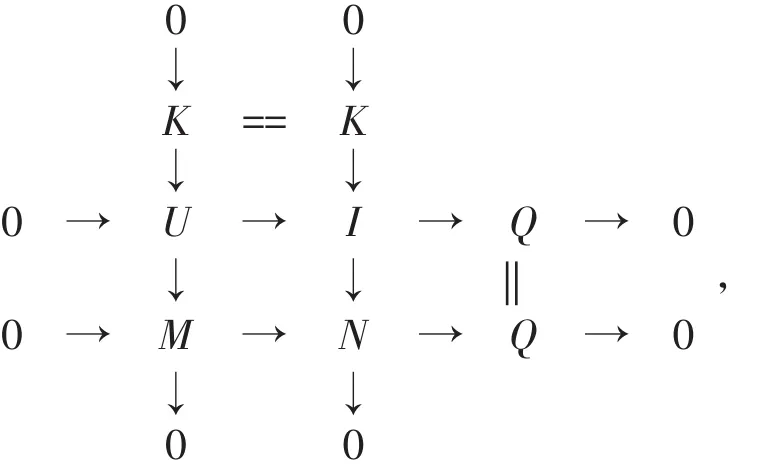
在短正合列0→K→U→M→0中K,M∈(X，I)-GI，從而U ∈(X，I)-GI。

考慮正合列0→U→I→Q→0，由定理1知Q ∈(X，I)-GI。

由定理2及文獻[1]中命題1.4不難得到下面的推論。

推論1 模類(X，I)-GI關于直和因子封閉。

定理3 設N是左R-模，則以下條件等價：

(1)存在短正合列0→G1→G0→N→0，其中G0,G1∈(X，I)-GI；

(2)對任意正合列0→H1→H0→N→0，其中H0∈(X，I)-GI且Ext1R(I,H1)=0(任意I∈I)，都有H1∈(X，I)-GI。

證明 (2)?(1)顯然成立，下面證明(1)?(2)。設存在短正合列0→G1→G0→N→0，其中G0,G1∈(X，I)-GI。由定理2知模類(X，I)-GI是內射可解的，所以N∈(X，I)-GI。由定理1知存在正合列0→K→I→N→0，其中I∈I且K∈(X，I)-GI。 對 任 意 正 合 列 0→H1→H0→ N → 0，其中H0∈(X，I)-GI且Ext1R(I,H1)=0(任意I∈I)，考慮如下拉回圖：

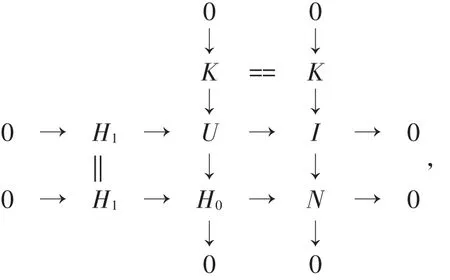
在正合列0→K→U→H0→0中K,H0∈(X，I)-GI，可見U ∈(X，I)-GI。用函子 HomR(I，-)作用于正合列0→H1→U→I→0可得長正合列

又因為I∈I ，Ext1R(I,H1)=0，所以0→H1→U→I→0可裂。H1是U的直和因子，由推論1可知H1∈(X，I)-GI。

[1]HOLM H.Gorenstein homological dimensions[J].J Pure Appl Algebra,2004,189(1-3):167-193.

[2]PAN Q X,CAI F Q.(X,Y)-Gorenstein projective and injective modules[J].Turkish J Math,2015,39:81-90.

[3]ENOCHS E E,JENDA O M G.Relative homological algebra[M].Berlin:Walter de Gruyter,2000:68-79.

[4]MENG F Y,PAN Q X.X-Gorenstein projective and Y-Gorenstein injective modules[J].Hacettepe Math,2011,40:537-554.

[5]ANDERSON F W,FULLER K R.Rings and categories of modules[M].New York:Spring Verlag,1992:177-241.

[6]佟文廷.同調代數引論[M].北京:高等教育出版社,1996:118-150.