某雙轉子發動機變態相似模型設計與驗證分析

丁 一，羅貴火，王 飛

(南京航空航天大學 能源與動力學院 江蘇省航空動力系統重點實驗室， 南京 210016)

轉子系統作為旋轉機械的核心部件，在現代工業尤其是航空、能源、電力等領域有著舉足輕重的作用[1]。模型試驗法是當前研究轉子系統動力學特性的最重要的方法之一，旨在通過與原型相似的模型試驗進行研究，從而得到原型的工作性能和規律特點[2]。根據不同的比例尺性質，模型試驗法所采取的試驗器可以分為2種，即正態模型和變態模型。對于與原型相同材料的正態模型，其固有頻率需要比原型大很多才能滿足動力學相似，其要求轉速在現有的試驗條件下往往無法達到，另外其所需的激勵頻率也比原型大很多。因此，采用變態模型轉子進行試驗不僅可以拓寬試驗的應用范圍，還可以減少模型制作的材料用量，從而降低試驗成本。國內外學者對變態模型相似性問題進行了研究并取得了豐碩成果，但對轉子系統動力學相似問題的研究不夠全面，尤其是轉子系統的動態響應方面的相似性問題研究極少。另外，轉子系統的動力相似尤其是變態動力相似方面的研究只停留在起步階段。因此，深入研究轉子系統動力模型變態相似問題和發展轉子系統變態模型優化設計方法是十分有必要的，對轉子系統試驗模型的相似設計具有重要意義。

本文在深入分析轉子系統變態模型、原型相似準則和動力學相似關系的基礎上，提出了基于數學模型的轉子變態模型優化設計思路和算法，并對實際發動機轉子系統進行了動力學相似設計。本文所采用的思路、分析方法和結論對轉子系統試驗模型的變態相似優化設計具有參考意義。

1 轉子系統動力變態相似準則關系

1.1 變態模型相似理論

變態模型不同維度的幾何尺寸不是按照相同比例縮小，即模型與原型分別對應的尺寸比例并不完全相同，變態相似也稱差似[3]。

如圖1所示，變態模型與原型的各個維度尺寸比例分別為l′/l=Cl、w′/w=Cw、h′/h=Ch，且Cl、Ch和Cw不全相等。三者全部都不相等時，稱為二維變態相似，某一對相等時，稱為一維變態相似[4]。變態率η表示的是2個不同維度的比例尺的比例，比如Cl和Ch：

(1)

對于任何變態模型，雖然3個不同維度方向上的幾何比例尺不同，但是時間比例尺均相等，即Ctl=Ctw=Cth，則變態模型的各個維度方向的關于速度v和加速度a的相似比關系為[5]：

(2)

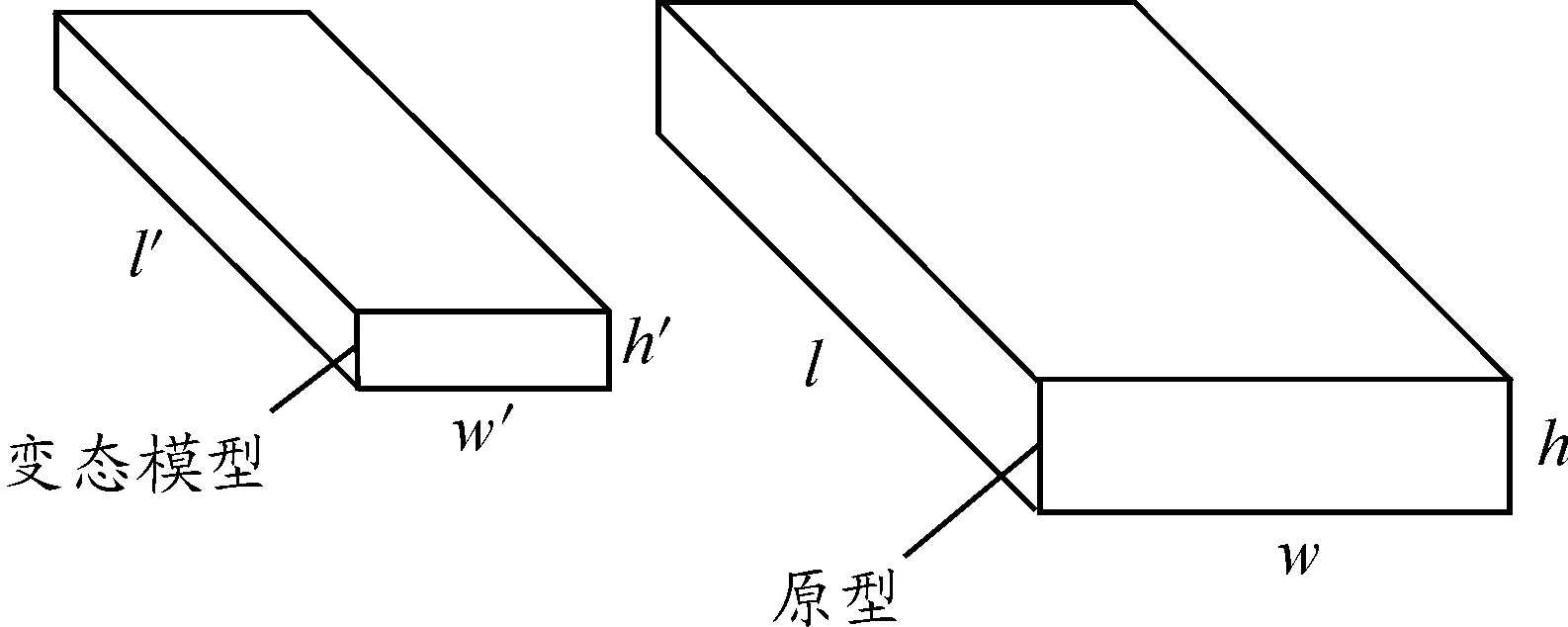
圖1 變態模型與原型示意圖

1.2 轉子系統變態模型的相似關系

本文研究對象軸向和徑向比例尺的基本量綱均為長度，無法用量綱分析或定律分析法推導出相似準則，因此采用方程分析法來推導轉子系統變態模型與原型的相似準則。轉子系統動力特性的數值分析方法主要有有限元法和傳遞矩陣法[6]。傳遞矩陣法應用最廣泛，但在求解高速轉子系統振動問題時經常會遇到數值極不穩定的情況[7]，并且與有限元法建立的模型相比，傳遞矩陣法一般不夠精確。因此，本文運用有限元法建立轉子系統的運動微分方程，從而推導相似準則和相似關系。

對于轉子系統的運動微分方程[8]：

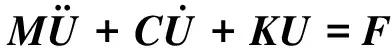
(3)

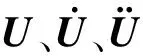
基于方程(3)，轉子系統變態模型的運動方程可分別表示為(變態模型下標為m，原型下標為p)：

(4)

假設剛度矩陣Km和Kp的相似比為CK，質量矩陣Mm和Mp的相似比為CM，阻尼矩陣Cm和Cp的相似比為CC，位移向量Um和Up的相似比為CU，外力向量Fm和Fp的相似比為CF，時間tm和tp的相似比為Ct，軸向尺寸lm和lp的相似比為Cl，徑向尺寸dm和dp的相似比為Cd，密度ρm和ρp的相似比為Cρ，彈性模量Em和Ep的相似比為CE，代入式(4)，化簡得：

(5)

方程(5)中各系數必須相互相等，才能使變態模型與原型相似，從中得出轉子系統變態模型與原型的相似準則：

(6)

則轉子系統動力學變態相似關系為：

(7)

對于固有頻率，其相似關系為

(8)

此外，激勵頻率比Cω0等于固有頻率比Cf。由于剛度系數k=mω2，阻尼系數c=2ξmω，那么彈性系數Ck和阻尼系數Cc相似關系為：

(9)

標記{ψr}m和{ψr}p分別代表變態模型和原型轉子的第r階振型，那么對于同一個測點，其位移維度的比例尺關系依舊為Cd，本質上振型的關系即測點上的復幅值比值。經過標準正則化，可以得到變態模型和原型轉子的振型關系：

{ψr}mn={ψr}pn

(10)

由式(10)可得，變態模型與原型轉子的同階模態振型完全一致。一般情況下，轉子系統的試驗器模型使用和原型轉子相同的材料，由此可得CE=Cρ=1。用λ代替Cl，表1列出了轉子系統變態模型的相似常數。

表1 轉子系統變態模型的相似常數

2 原型雙轉子系統動力特性分析

為進行動力相似設計，首先需要了解原型轉子系統的動力特性。某渦輪軸發動機耦合雙轉子系統由動力渦輪轉子(內轉子)和燃氣發生器轉子(外轉子)構成，見圖2、3。

圖2 動力渦輪轉子

圖3 燃氣發生器轉子截面

內轉子動力渦輪轉子共有4個支承，支承編號為1、2、5、6；外轉子燃氣發生器轉子共有2個支承，支承編號為3和4；6個支承的支承剛度數值見表2。

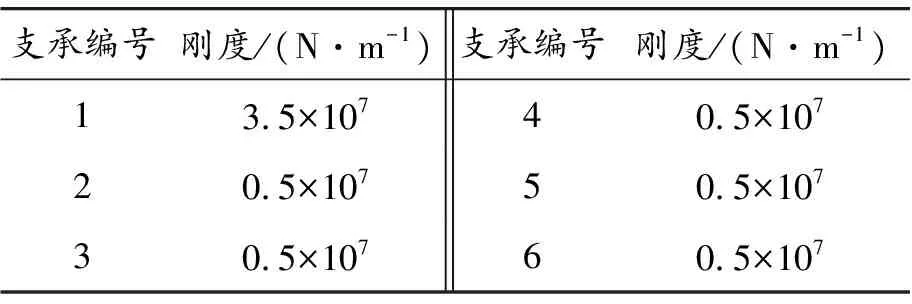
表2 轉子各支承剛度

本文采用有限元方法計算原型轉子的臨界轉速。其中，燃氣發生器轉子有限元模型采用四節點四邊形SOLID272單元進行網格劃分，采用集中質量單元(包含質量與轉動慣量)模擬各級壓氣機轉子葉片、渦輪葉片及部分輪盤，忽略流體流動產生氣動力的影響。整個模型共有37 284個節點，7 838個單元，2個軸承單元，6個集中質量單元。計算所得到的動力渦輪轉子臨界轉速對比見表3，燃氣發生器轉子臨界轉速對比見表4。

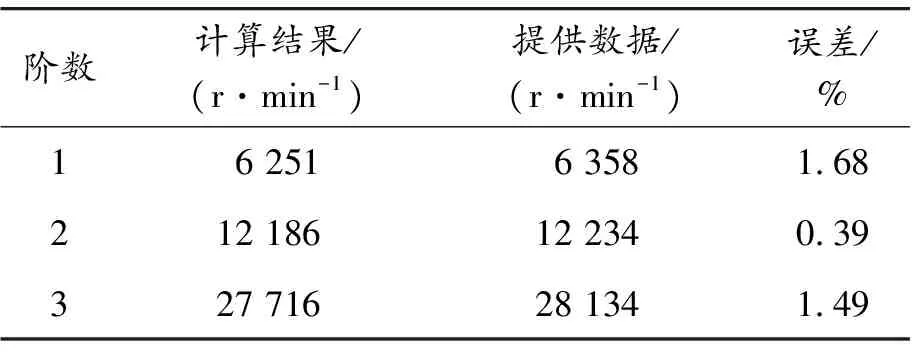
表3 動力渦輪轉子臨界轉速對比

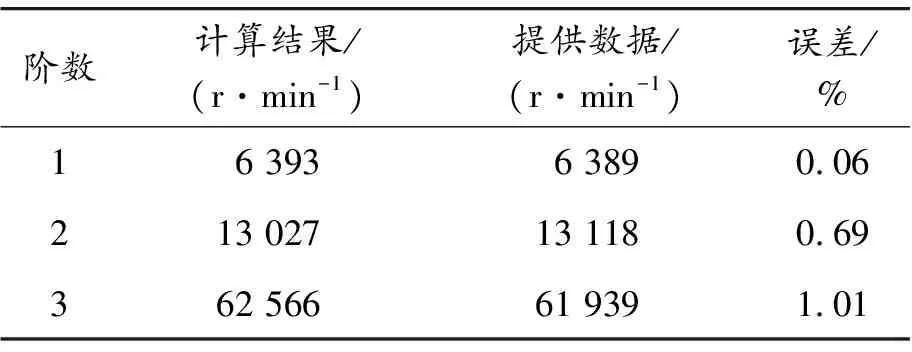
表4 燃氣發生器轉子臨界轉速對比

從表3和表4的結果可以看出：采用有限元法計算的原型轉子系統臨界轉速和提供數據的最大誤差僅為1.68%，計算結果精確，滿足航空發動機工作轉速上下邊界距臨界轉速20%以上裕度的設計要求。

3 雙轉子系統相似模型設計

為了進行轉子系統動力模型試驗，需要先選擇合適的模型相似律并進行縮比模型的設計工作[9-10]。實踐證明，與原型π準則完全相同的模型設計方法往往無法滿足特定的固有頻率或動態響應等設計指標。轉子系統變態模型與原型π準則不全相等，所以需要尋求轉子系統變態模型設計的指導方法。

3.1 相似比的選取

為進行動力相似設計，首先需要確定模型轉子與原型轉子之間的相似比。在確定相似比過程中主要考慮以下因素：

1) 試驗器設備限制角度：燃氣發生器轉子最大轉速為45 000 r·min-1，現有試驗器驅動電機最大轉速為9 000 r·min-1。考慮到電機驅動功率以及皮帶傳動方式，電機最大可以以傳動比1∶2工作。因此，模型轉子最大轉速為18 000 r·min-1，即要求相似比小于等于0.4；

2) 試驗安全角度：所選取的相似比不可過小，因為過小的相似比會導致轉子軸段的內徑過小，影響轉子軸的強度，不利于試驗的安全展開，因此相似比應大于0.2；

3) 其他方面：在允許范圍內，相似比應取較大數值：一方面可以保證軸具有較好的強度；另一方面可以使相似模型的支承剛度較大，增強彈性支承的強度，方便加工。

考慮上述因素，模型轉子的相似比取0.4。根據已推導的轉子系統變態模型的相似準則，建立變態率η為2.5的轉子系統變態模型，其軸向比尺為1，徑向比尺為0.4。所有相關參數均嚴格按照相似關系進行相似變換，各轉子系統變態模型的基本數據如表5所示。

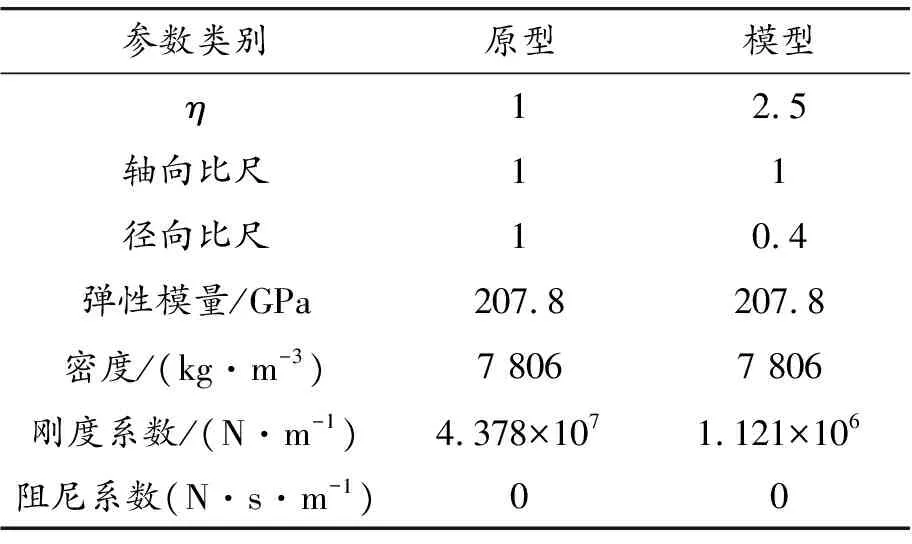
表5 轉子系統變態模型的基本參數

3.2 試驗器特征參數優化

本文采用逆向思維的設計方法，通過調整轉子模型的特征參數來滿足設計目標，計算方法采用與第2部分一致的有限元方法，優化方法采用遺傳算法，二者結合設計試驗器模型轉子[11]。如圖4所示，該算法通過有限元與遺傳算法的接口程序，由遺傳算法對初始配置進行優化，從而找到最優的設計變量，得到最佳設計結果。

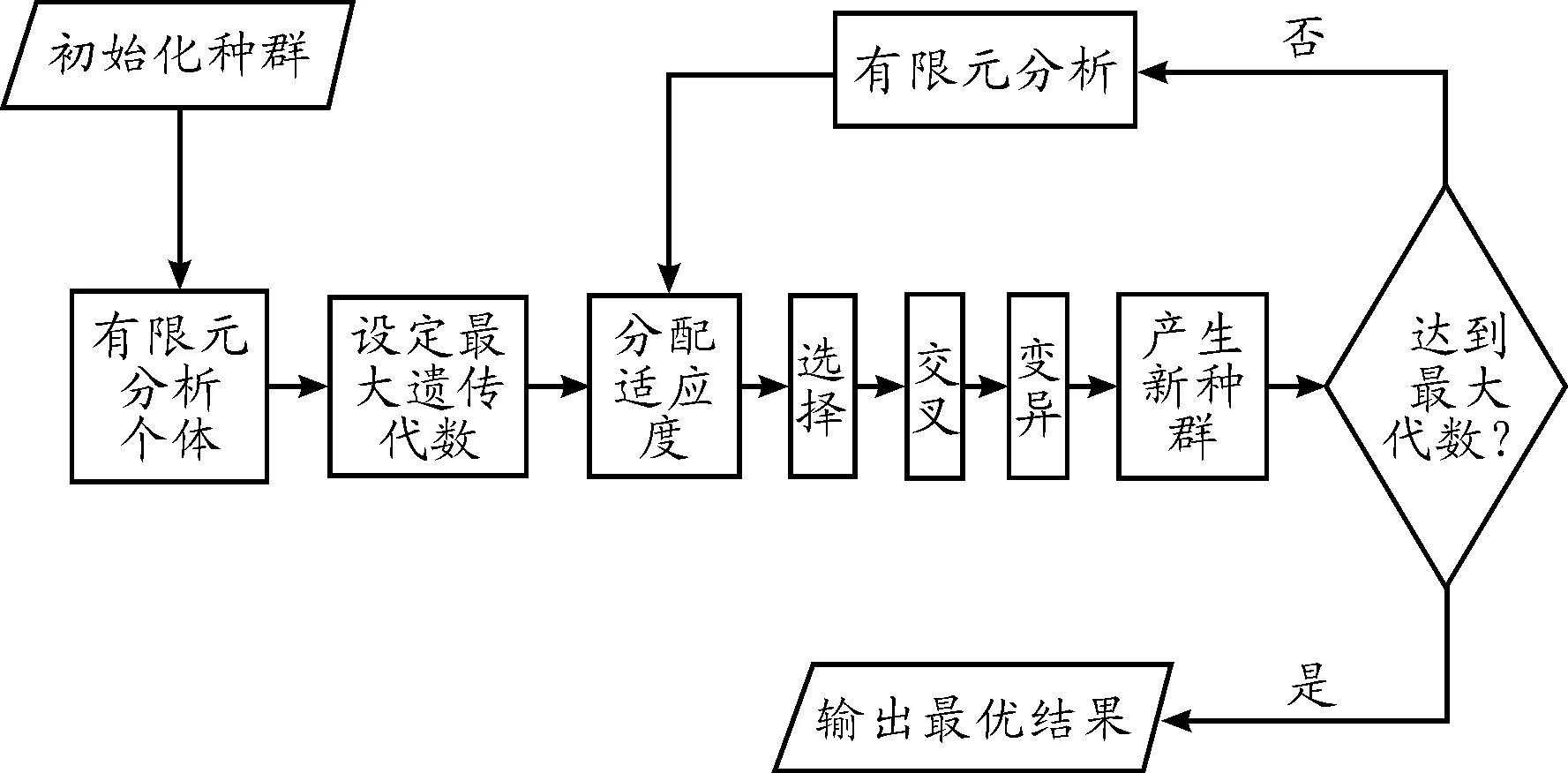
圖4 有限元法與遺傳算法結合優化設計流程

轉子系統具有3個獨立的相似元：剛性盤、轉軸和軸承。本文研究對象的特征參數有2段軸的直徑和長度、8個圓盤的直徑和厚度、6個軸承的支承阻尼和支承剛度。基于試驗的現實意義，本研究選取6個支承剛度相似常數作為優化設計變量。此外，根據實際工程意義和價值對優化設計變量的取值范圍進行界定，本文選取試驗器轉子的質量和工作轉速下的不平衡響應作為約束條件。優化目標函數的選取一般為試驗器轉子系統和原型轉子的固有頻率、振型或位移響應等，如式(11)所示，以達到真實模擬原型轉子的動力學特性等目的。其次，轉子試驗器模型的優化設計也用于提高模型的動力特性以降低轉子系統的振動水平[12]。

(11)

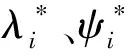
對于本文的研究對象，設計變量取各支承剛度，優化目標函數如式(12)所示：

(12)

其中：λ=0.4為指定的相似比；wi,i=1,2,3為模型轉子系統前3階臨界轉速；Ωi,i=1,2,3為動力渦輪轉子或燃氣發生器轉子系統的前3階臨界轉速。

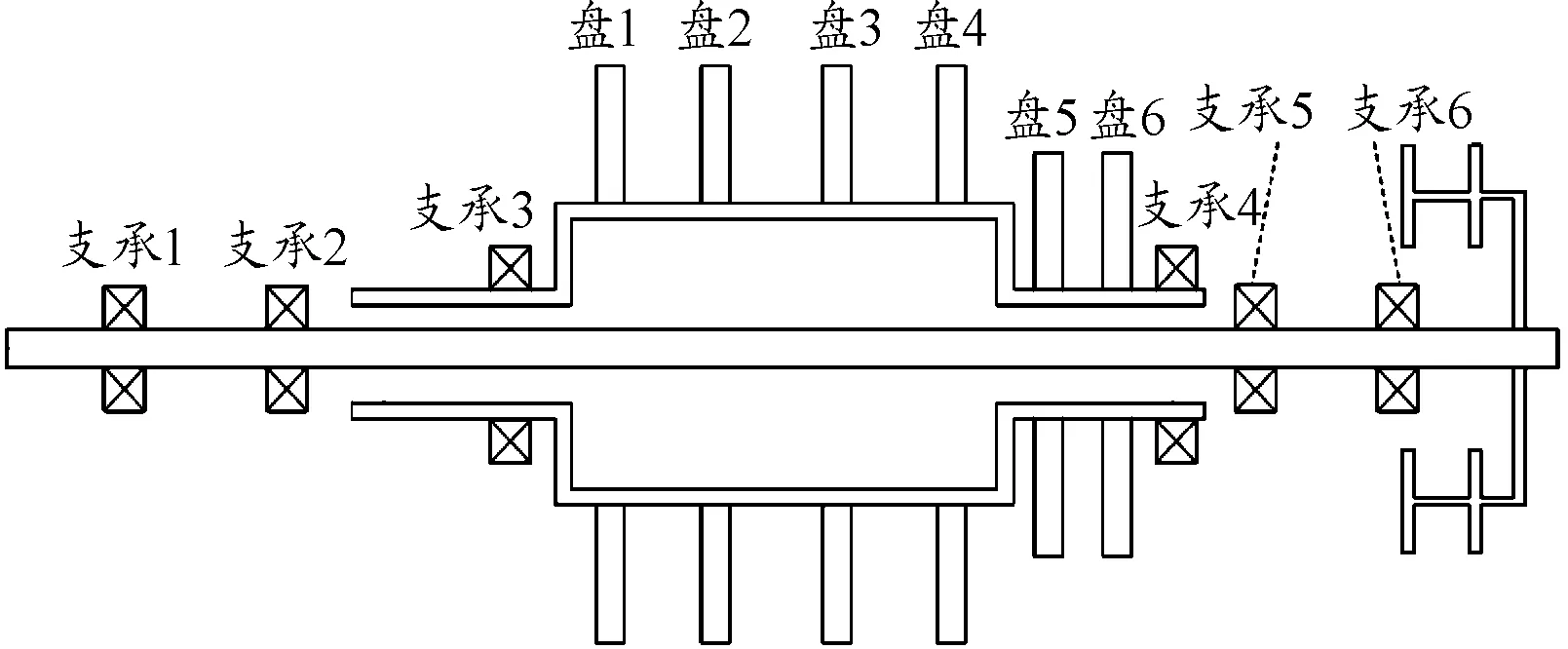
圖5 相似模型轉子示意圖

所設計的試驗器轉子示意圖如圖5所示，與原型一致。動力渦輪模型轉子(內轉子)由4個彈性支承、1個輪盤以及軸組成。燃氣發生器模型轉子(外轉子)由2個支承、6個輪盤以及軸組成。6個支承均采用滾動軸承和鼠籠式彈性支承以及擠壓油膜阻尼器的形式構成。優化后的動力渦輪試驗器轉子支承1、2、5、6的各剛度見表6，燃氣發生器試驗器轉子支承3、4的各剛度見表7。

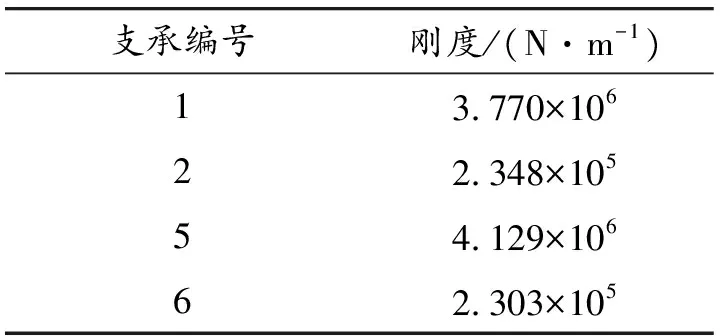
表6 優化后動力渦輪模型轉子支承剛度

表7 優化后燃氣發生器模型轉子支承剛度

3.3 試驗器轉子鼠籠式彈性支承設計

根據求得的6個支承的剛度，進行鼠籠式彈性支承的設計。通過參數化建模設計可得到6個鼠籠尺寸的長、寬、高，如表8所示。其中，籠條根部倒角為R1。

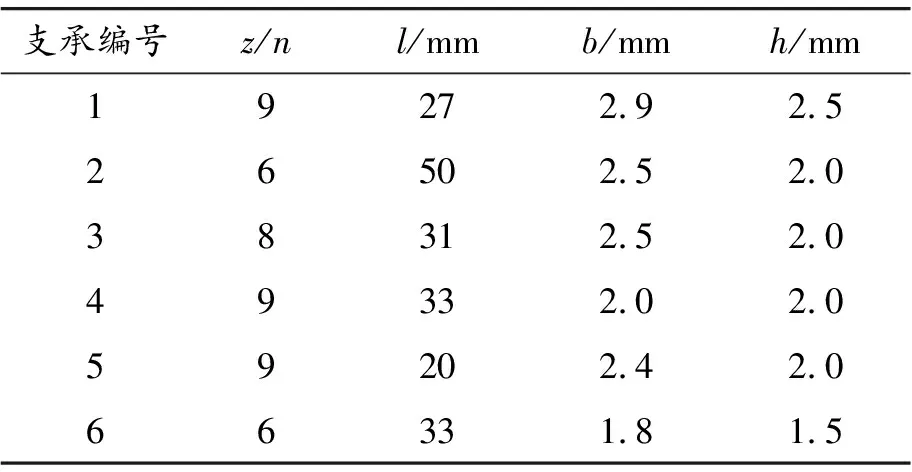
表8 試驗器轉子彈性支承參數

為確定設計的鼠籠彈性支承滿足剛度要求，將設計的鼠籠通過UG建立模型，利用有限元法進行剛度計算。考慮到鼠籠彈支的結構較復雜，部分結構比較細小，選用10節點的solid187單元，進行自由網格劃分，同時設置smrt=1，得到的有限元模型如圖6所示。

圖6 試驗器轉子彈性支承的有限元模型

表9給出了各個彈性支承有限元計算求解剛度與目標剛度的誤差，可以看出剛度的誤差在8%以內，滿足彈性支承的設計指標要求。

4 試驗器轉子動力特性分析與驗證

4.1 動力渦輪試驗器轉子

采用有限元法，動力渦輪試驗器轉子前3階臨界轉速與原型的對比見表10。

從表10中可以看到：模型轉子系統各階臨界轉速均為原型轉子各階臨界轉速的0.4倍，最大誤差僅為2.94%；從圖7可得：前2階臨界振型均為1階彎曲，第3階振型為2階彎曲，模型轉子與原型轉子系統前3階臨界振型的mac值均大于0.91，即兩者的相似度大于91%。以上分析表明：本文設計的動力渦輪模型轉子能較好地反映原型轉子的動力特性，達到轉子系統變態相似試驗模型的設計要求。

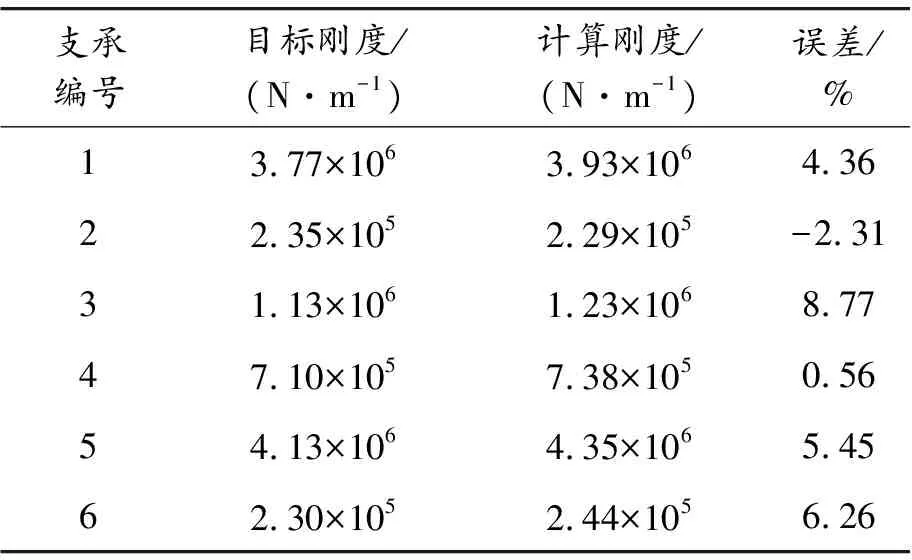
表9 試驗器轉子彈性支承剛度計算結果

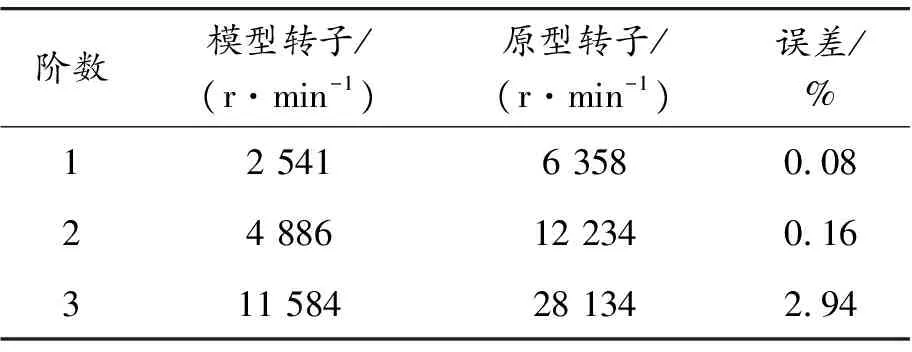
表10 動力渦輪模型轉子與原型轉子臨界轉速對比

4.2 燃氣發生器試驗器轉子

同樣采用有限元法，燃氣發生器試驗器轉子前3階臨界轉速與原型的對比見表11。

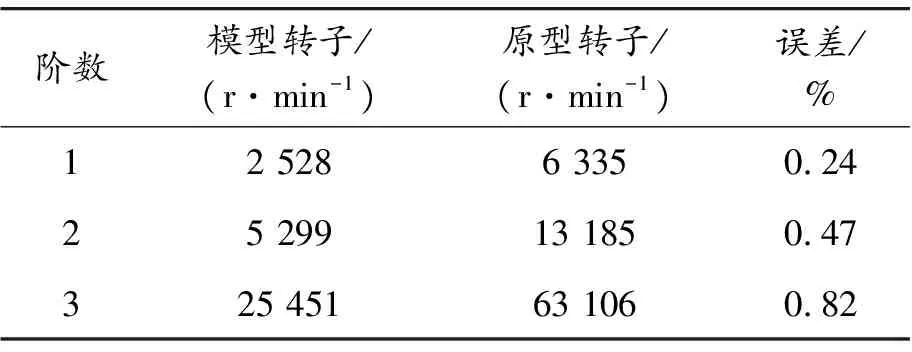
表11 燃氣發生器模型轉子與原型轉子臨界轉速對比

從圖8中可以看出：模型轉子的前3階臨界振型分別為整體渦動、俯仰振型和1階彎曲。表11顯示：模型轉子各階臨界轉速均為原型轉子臨界轉速的0.4倍，最大誤差僅為0.82%。以上分析表明，本文設計的燃氣發生器模型轉子動力特性和原型轉子系統的動力特性高度吻合，誤差低于1%，為模型試驗提供良好的理論基礎和精度保證。

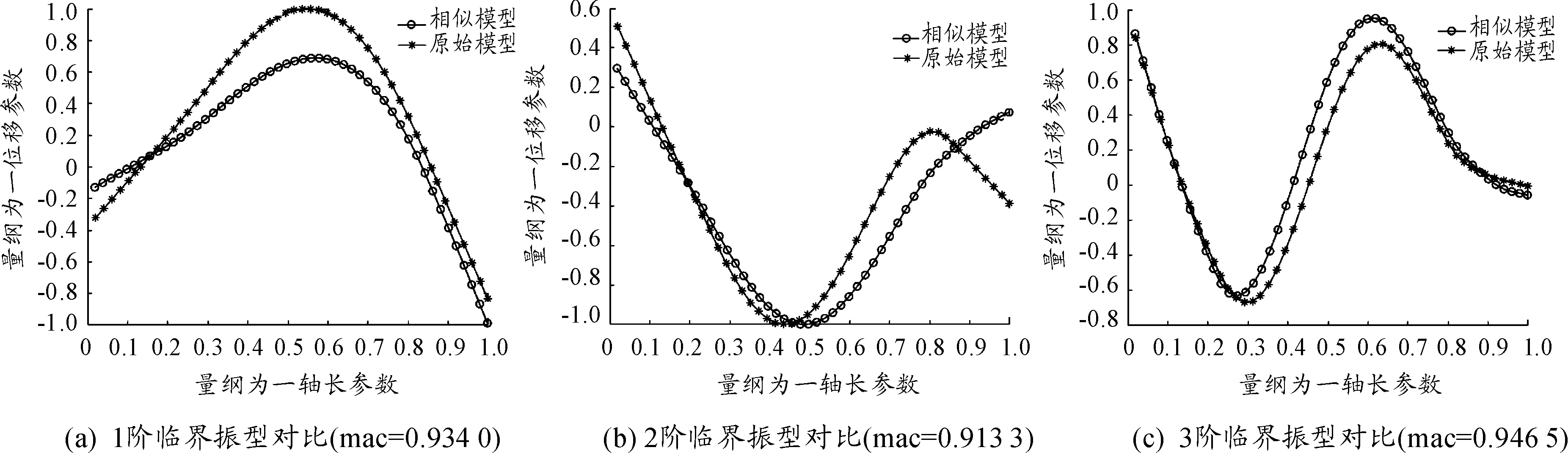
圖7 動力渦輪模型轉子與原型轉子臨界振型對比

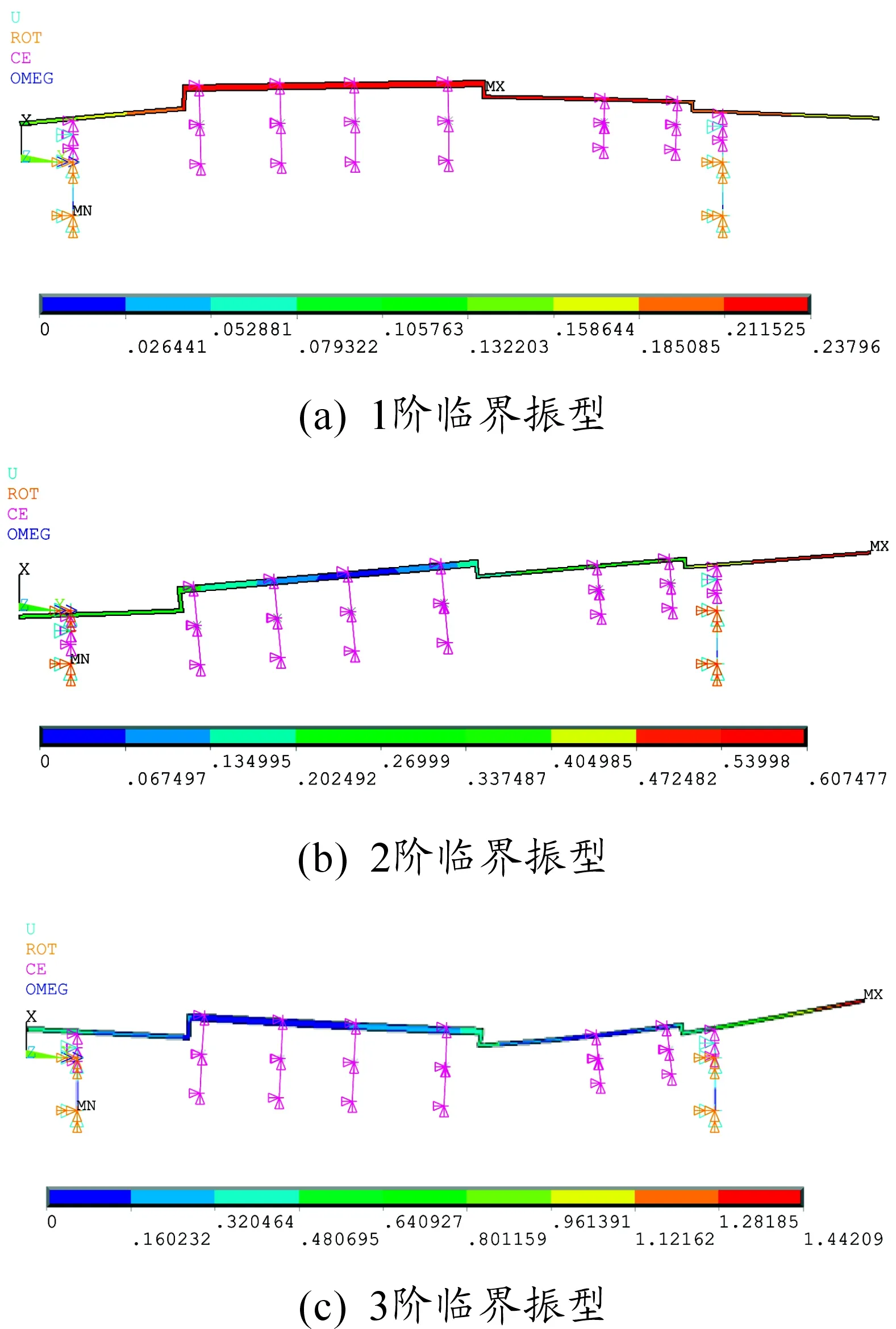
圖8 燃氣發生器模型轉子臨界振型

5 結束語

本文對某型雙轉子渦軸發動機進行了變態動力相似優化設計和驗證分析，計算結果表明動力渦輪外轉子臨界轉速的誤差為2.94%，燃氣發生器內轉子臨界轉速的誤差為0.82%，各階振型的mac值均達到了90%以上。因此，本文所設計的試驗器模型與原型轉子滿足動力學相似，能高精度地相似反映原型轉子的動力學特性。轉子系統變態模型動力相似設計方法切實可行，為轉子系統的模型試驗研究提供理論支撐。此外，本文所提出的相似參數選取、特征參數優化、鼠籠彈性支承設計驗證等一系列方法和算例對轉子系統試驗器的相似設計具有一定的指導意義。

[1] 馮志鵬，宋希庚，薛冬新.旋轉機械振動故障診斷理論與技術進展綜述[J].振動與沖擊，2001，20(4)：36-40.

[2] TAIBIEI A.Structural similitude and scaling laws forcross-ply laminated plates[J].AIAA Journal,1997,35(10):1669-1671.

[3] BAKER W E.Similarity Methods in Engineering Dyna-mics[M].New Jersey:Hayden Book Company,1973:30-35.

[4] 王旭冕，黃廷領，劉勇.管流變態模擬的相似理論研究[J].西安建筑科技大學學報，2006，38(2)：294-296.

[5] 黃禮坤.轉子系統動力模型變態相似分析及設計方法研究[D].長沙：中南大學,2013.

[6] RAFFA F A,VATTA V.The dynamic stiffness method for linear rotor-bearing system[J].ASME Journal of Vibration and Acoustics,1996,118(7):332-339.

[7] 肖明杰，黃金平，李峰.基于傳遞矩陣法的渦輪轉子系統瞬態動力學特性預測與分析[J].機械強度，2011,33(6):900-906.

[8] 許濤.彈性支承-柔性軸轉子系統動力學研究[D].西安：西安電子科技大學，2010.

[9] GANG X Y,WANG D F,SU X J.A new similitude ana-lysis method for a scale model test[J].Key Engineering Materials,2010,439:704-709.

[10] 劉占卿，王東峰，張志成.縮比試驗模型設計與驗證[J].計算機仿真，2008，25(8)：51-54.

[11] 彭文杰，陳建橋，顧明凱.基于粒子群算法ANSYS的層合板自由邊界層間正應力的優化研究[J].機械科學與技術，2009，28(11)：1496-1500.