微咸水入滲條件下的一維代數模型研究

畢 遠 杰

(山西省水利水電科學研究院，太原 030002)

0 引 言

土壤水分入滲過程受到諸多因素的影響，其中入滲水水質就是其主要影響因素之一。入滲水中所含化學物質隨入滲水分進入土壤后，與土壤中原有的化學物質及土壤顆粒之間發生物理化學作用，從而導致土壤孔隙分布特征發生改變，進而影響作物對土壤水分和養分的吸收[1,2]。隨著淡水資源的日益緊缺，除了采取一定的措施提高淡水資源的利用效率外，合理開發利用微咸水資源已成為緩解水資源供需矛盾的有效途徑。國內外學者從入滲水礦化度[3-5]、入滲水量[6]、土壤初始條件[7]、土壤質地[8,9]等方面就微咸水入滲特征及理論做了大量的研究，結果表明微咸水入滲后土壤結構發生改變，從而導致其土壤水分入滲特性發生改變。史曉楠[10]、吳忠東[11]、栗濤[12]等利用一維代數入滲模型和Green-Ampt模型分析微咸水入滲過程，結果表明兩模型均可以用于描述微咸水入滲土壤水分運動及分布規律，但由于微咸水入滲改變了傳統淡水入滲公式推求的基本條件，從而導致淡水入滲模型描述微咸水入滲時計算的誤差相對較大。因此，如何將入滲水的水質因素融入模型，是改善淡水入滲模型對微咸水入滲計算精度的關鍵。

論文首先采用一維代數模型模擬微咸水入滲土壤含水率分布，在對模擬結果對比分析的基礎上，對淡水入滲條件下的一維代數模型進行改進，把微咸水入滲對土壤水分入滲特性的影響歸結為土壤孔隙率發生改變的結果，建立微咸水入滲條件下的一維代數模型，并對模型進行驗證。論文所建立的微咸水入滲條件下的一維代數模型僅通過代數計算就可以推求出土壤水分運動特征，減少了數值計算過程所引起的誤差，為預測預報微咸水灌溉條件下的土壤水分特征提供了準確、便捷的方法。

1 一維代數模型在微咸水入滲中的應用

1.1 一維代數模型

一維代數模型是王全九等[13]推求的一種適用于描述恒定水頭條件下土壤一維積水入滲過程的土壤水分運動數學模型，該模型計算過程簡單，其代數計算過程可有效減小由于數值計算所引起的誤差。當土壤初始含水量較低時，取滯留含水量等于土壤初始含水量，一維代數模型可以表達為：

(1)

(2)

(3)

式中：i為入滲率，cm/min；ks為飽和導水率，cm/min；β為非飽和土壤吸力分配系數，1/cm；zf為濕潤鋒推進距離，cm；I為累積入滲量，cm；θs為土壤飽和含水量，cm3/cm3；α為土壤水分特征曲線和非飽和導水率綜合性狀系數；θi為土壤初始含水量，cm3/cm3；θ為土壤含水量，cm3/cm3；z為土體中任意一點距離土表的深度，cm。

由式(1)～(3)可知，在應用一維代數模型分析土壤水分運動特征時，α、β和ks需要根據試驗資料確定，而θs、θi是土壤水分基本參數，可通過試驗獲得。

明確了累積入滲量與濕潤鋒的關系，計算出α值后，土體中任意一點的土壤含水量便可以由式(3)計算得出。

1.2 微咸水入滲試驗

礦化度和鈉離子相對含量是微咸水兩個重要的水質指標，鈉離子相對含量一般用鈉吸附比(簡寫做SAR)表示。研究表明[14]：入滲水的礦化度(簡寫做C)和鈉吸附比均一定程度的影響土壤水分入滲特性。本文為了分析不同礦化度和鈉吸附比組合的微咸水入滲特性，選擇了8種不同的微咸水進行了一維積水入滲試驗。

供試土樣容重1.42 g/cm3，初始含水量4.8%，飽和含水量49.8 %，土壤顆粒組成及主要離子含量列于表1中。

表1 土壤顆粒組成及主要離子含量

利用式(2)對8組不同水質入滲的實測資料對累積入滲量與濕潤鋒推進深度間關系進行擬合，并計算相應的α值，結果如表2所示。

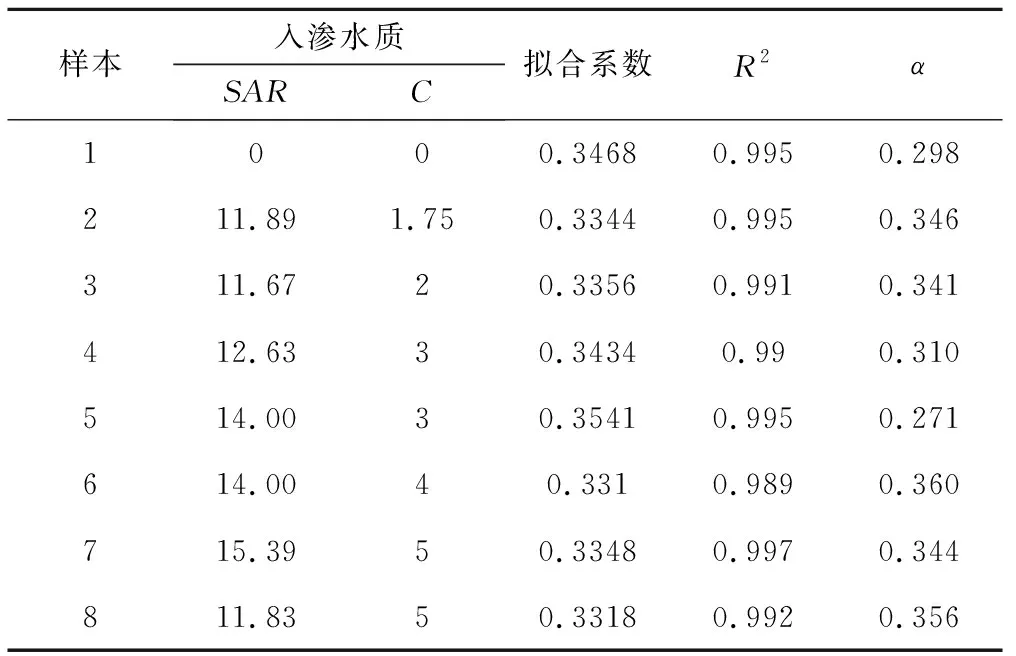
表2 擬合及計算結果

將α值帶入式(3)，計算得到土體中任意一點的含水率值，將不同入滲水質入滲后的土壤含水量實測值與計算值進行對比，如圖1所示。從圖1可以看出，入滲水為蒸餾水時，計算的土壤含水量與實測值吻合較好，其余處理計算值與實測值之間差別較大，且主要表現為上層土壤計算含水量小于實測值，下層土壤則恰恰相反，這也從某種角度說明了微咸水入滲后改變土壤結構特征，降低土壤保水能力。在8組試驗數據中，含水量計算值與實測值相對誤差的絕對值介于0.17%～15.76%之間，剖面含水量計算值與實測值的平均相對誤差介于1.38%～16.72%之間，可見，采用一維入滲模型計算微咸水入滲時，計算結果均可以反映土壤水分分布特征，但計算精度受水質指標影響較大，其計算精度得不到保證。

2 微咸水入滲條件下的一維代數模型

2.1 模型建立

由于微咸水滲入到土壤后導致土壤結構及孔隙性改變，因此把微咸水入滲對土壤水分入滲特性的影響歸結為土壤孔隙率發生改變的結果，而土壤孔隙率改變在一維代數模型中則反應在土壤飽和含水量上，這樣，一維代數模型可以寫作：

(4)

(5)

式中：λ為土壤孔隙率變化系數；其他符號意義同前。

2.2 參數確定

在分析不同水質入滲條件下的入滲資料時發現，相同的入滲時間內，入滲水質不同，濕潤鋒推進距離不同，土壤累積入滲量亦有所不同。定義入滲結束時累積入滲量與濕潤鋒推進距離的比值為整個濕潤體平均含水量，結果發現，不同入滲水質入滲后，濕潤體平均含水量不同。這種差別間接地反映了土壤孔隙性的變化，因此，以此為出發點，尋求微咸水入滲后土壤孔隙性變化的規律。

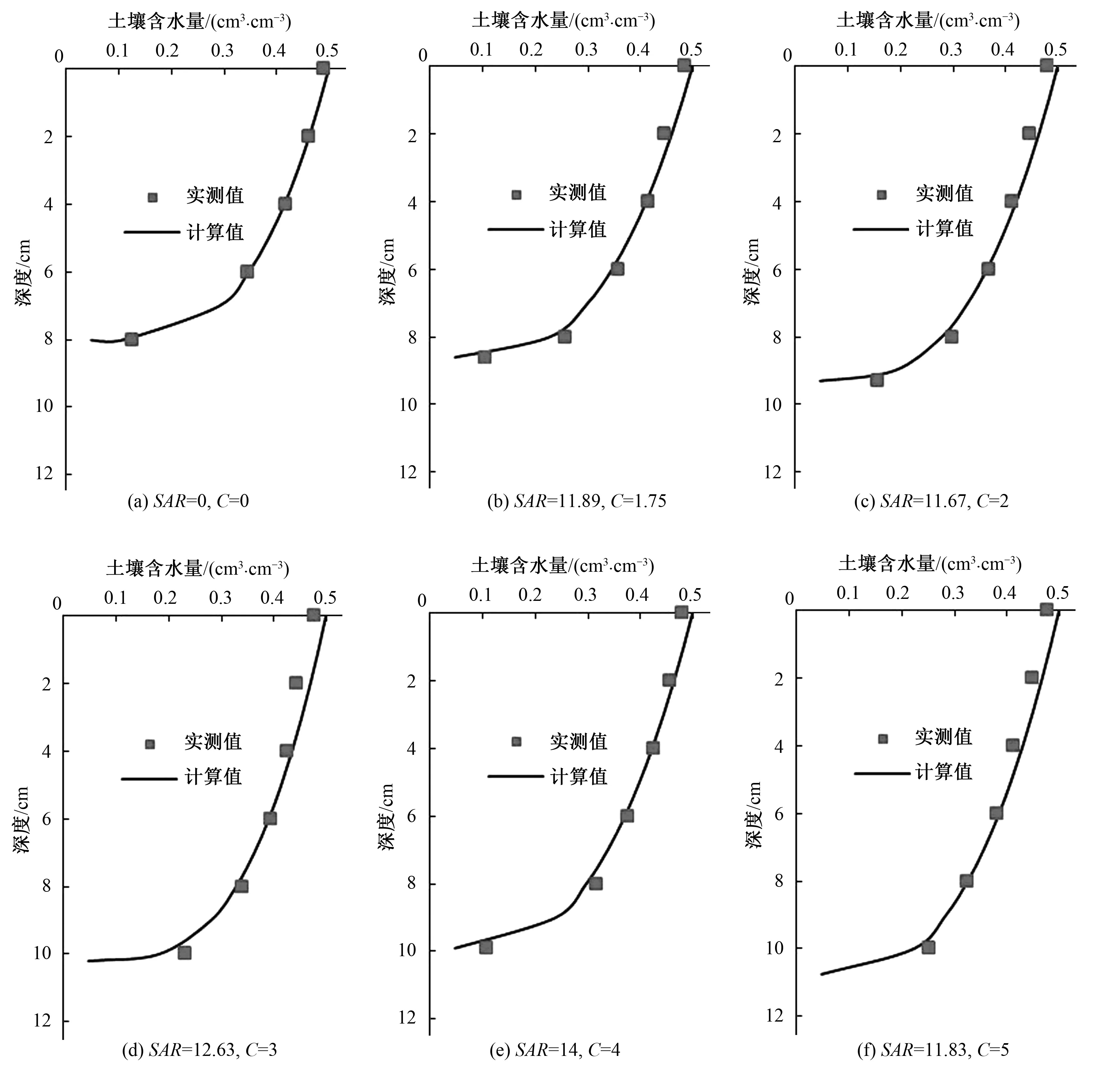
圖1 含水量實測值與計算值對比圖

上述分析中發現，對于入滲水質為蒸餾水的情況，用一維代數模型計算其含水量剖面的結果較為理想。為了進一步分析其計算含水量與實測含水量之間的差別，特利用線性函數對計算含水量和實測含水量進行擬合，擬合結果見式(6)，從擬合結果可以看出，計算的含水量和實測的含水量之間的相對誤差分別為0.3%，可見計算精度較高。因此，假定采用這種水質入滲對土壤孔隙性沒有影響，進而以該入滲水條件下的濕潤體平均含水量作為對照，其他水質入滲后的濕潤體平均含水量與其比值作為該入滲水質入滲條件下土壤孔隙率變化系數。土壤孔隙率變化系數計算過程見表3。

θ計算=0.997θ實測R2=0.996

(6)

用實測資料擬合累積入滲量與濕潤鋒的關系后，將相應λ帶入(4)，便可計算出修正后的α值，將其帶入式(5)便可以計算出修正后的剖面含水量，計算結果與實測資料的對比如圖2所示。

由圖2可以看出，一維代數模型經過改進后，計算的含水量與實測值之間吻合較好，經計算知其最大相對誤差的絕對值不超過5%。

D K Singh[15]、Schwartzman and Zur[16]等研究表明地下滴灌的濕潤鋒與其影響因子之間呈較好的多元乘冪函數關系。

表3 土壤孔隙率變化系數計算

由上述分析可知，礦化度和SAR為影響微咸水入滲過程的主要因素，因此，在此對不同水質入滲水入滲后濕潤鋒與其影響因子之間的關系也采用zf=aSARbCc形式的多元乘冪函數擬合，擬合的相關系數較高，達到0.87。擬合結果見式(7)。

zf=21.879SAR-0.396C0.173R=0.87

(7)

式中：zf為入滲結束時濕潤鋒推進距離，cm。

圖2 含水量實測值與計算值對比圖

由上述分析可知，濕潤鋒推進距離與入滲水的SAR和礦化度之間呈較明顯的多元乘冪函數形式，而土壤孔隙率變化系數 與濕潤鋒推進距離有關，于是采用元乘冪函數形式對 與入滲水礦化度和SAR值進行擬合，發現擬合結果較為理想，其擬合的相關系數較高，達到了0.981。擬合結果見式(8)。

λ=0.872SAR0.046C-0.011R=0.97

(8)

這樣，微咸水入滲條件下的一維代數模型便可以寫作：

(9)

(10)

(11)

2.3 模型驗證

為了驗證上述模型的準確性及計算精度，采用另外兩組實測資料對其進行驗證，選用的兩組入滲資料其入滲水水質指標分別為：SAR=14.32，C=1.55；SAR=11.67，C=5.2。將其帶入式(8)計算得到λ分別為：0.981和0.959。累積入滲率與濕潤鋒之間的擬合結果為：I=0.367zf，R2=0.972；I=0.338zf，R2=0.969，因此α值分別為0.200和0.271，將其帶入式(11)計算剖面含水量，計算結果與實測資料的對比如圖3所示。

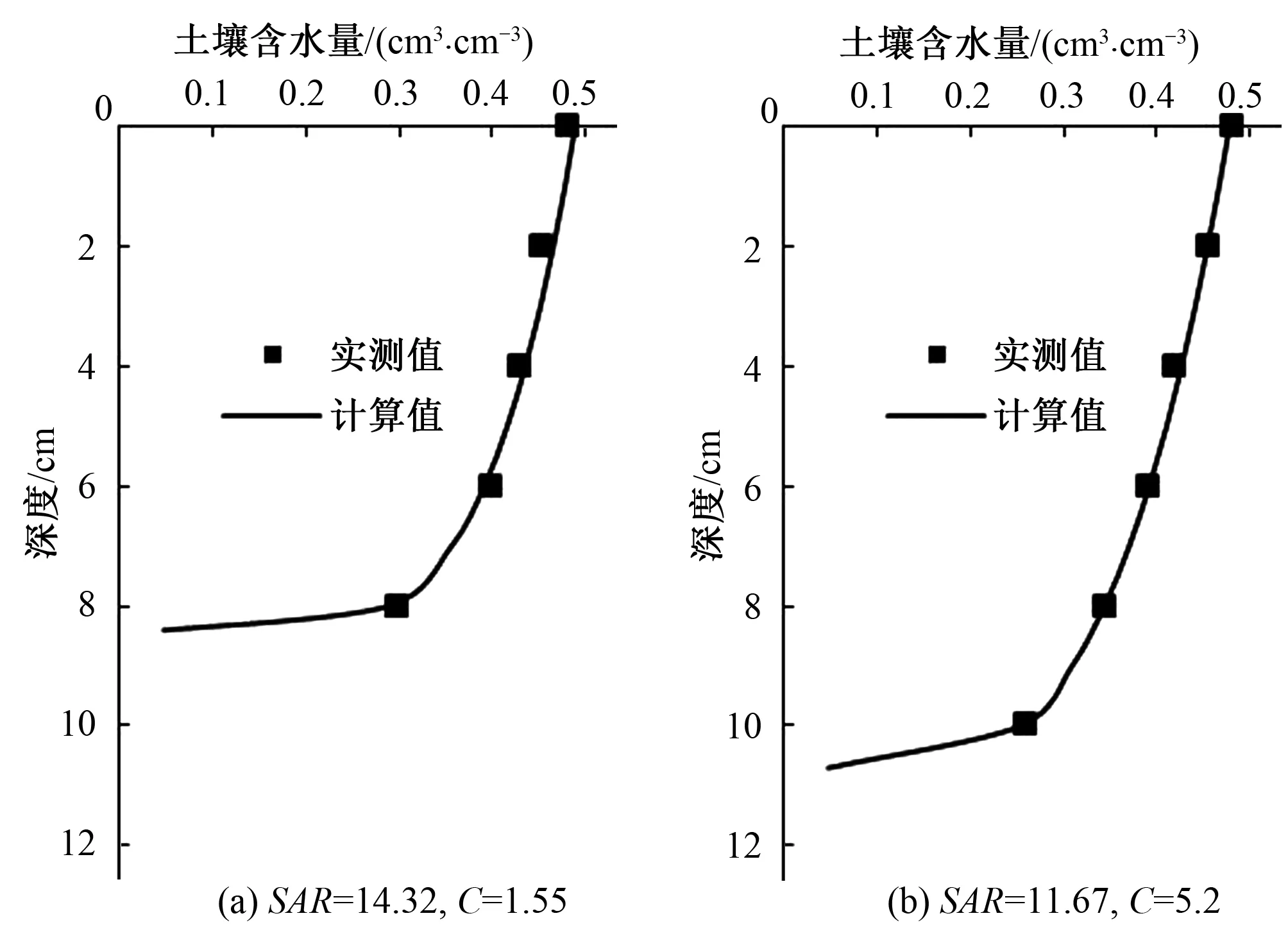
圖3 含水量實測值與計算值對比圖

利用線性函數對計算含水量和實測含水量進行擬合，擬合結果見式(12)及(13)，從擬合結果中可以看出，計算的含水量和實測含水量之間的誤差分別為1.1%和-1.8%，可見模型的計算精度較高。

θ計算= 1.011θ實測R2=0.989

(12)

θ計算= 0.982θ實測R2=0.994

(13)

3 結 論

在采用一維代數模型計算微咸水入滲土壤含水量時發現，計算值與實測值之間差別較大，且主要表現為上層土壤計算含水量小于實測值，下層土壤則恰恰相反。通過多組入滲資料的對比發現，采用一維入滲模型計算微咸水入滲時，模型均可以反映土壤水分分布特征，但計算精度受水質指標影響較大，其計算精度得不到保證。因此對淡水入滲條件下的一維代數模型進行改進，把微咸水入滲對土壤水分入滲特性的影響歸結為土壤孔隙率發生改變的結果，而土壤孔隙率改變在一維代數模型中則反應在土壤飽和含水量上，因此將土壤飽和含水量乘以一個土壤孔隙率變化系數 ，建立了微咸水入滲條件下的一維代數模型并對其進行驗證，結果表明計算的含水量和實測含水量之間的誤差較小，模型的計算精度較高。

參考文獻：

[1] Rhoades J D. The use of saline water for crop production[R]. Irrigation and drainage, Rome FAO, 1992．

[2] Oster J D. Irrigation with poor quality water[J]. Agricultural Water Manage, 1994,25:271-275．

[3] 劉婷姍，高艷明，李建設. 不同礦化度微咸水入滲下土壤水鹽運移特征研究[J]. 灌溉排水學報，2014，33(3)：68-72．

[4] 史曉楠,王全九,蘇 瑩,等.微咸水水質對土壤水鹽運移特征的影響[J].干旱區地理,2005,28(4):516-520.

[5] 郭太龍,遲道才,王全九,等.入滲水礦化度對土壤水鹽運移影響的試驗研究[J].農業工程學報,2005,21(Z1):84-87.

[6] 蘇 瑩,王全九,葉海燕,等.微咸水不同入滲水量土壤水鹽運移特征研究[J].干旱地區農業研究,2005,23(4):43-48.

[7] 王全九,葉海燕,史曉南, 等.土壤初始含水量對微咸水入滲特征影響[J].水土保持學報,2004,18(1):51-53.

[8] 楊 艷,王全九.微咸水入滲條件下堿土和鹽土水鹽運移特征分析[J].水土保持學報,2008,22(1):13-19.

[9] 趙麗麗,張振華,李陸生.濱海鹽漬土和棕壤咸水入滲特征分析[J].水土保持通報,2013,33(3):44-48,117.

[10] 史曉楠,王全九,巨 龍,等.微咸水入滲條件下Philip模型與Green-Ampt模型參數的對比分析[J].土壤學報,2007,44(2):360-363.

[11] 吳忠東，王全九. 利用一維代數模型分析微咸水入滲特征[J].農業工程學報，2007，23(6)：21-26.

[12] 栗 濤，王全九. 淡水入滲模型對咸水入滲過程的適用性[J].灌排機械工程學報，2014，32(1)：80-85.

[13] 王全九，邵明安，鄭紀勇．土壤中水分運動與溶質運移[M]．北京：中國水利水電出版社，2007：12-14.

[14] 王全九,單魚洋. 微咸水灌溉與土壤水鹽調控研究進展[J]. 農業機械學報，2015，(12):117-126.

[15] D K Singh, T B S Rajput, D K Singh, et al. Simulation of soil wetting pattern with subsurface drip irrigation from line source[J]. Agricultural Water Management, 2006,83(1-2):130-134.

[16] Schwartzman M, Zur B. Emitter spacing and geometry of wetted soil volume[J]. J. Irrig. Drain. Eng. 1986,112(3):242-253.