基于混合算法的智能電表計量自動化研究?

魯觀娜 呂言國 李文文 姜振宇 黃 凡

（1.國網冀北電力有限公司電力科學研究院 北京 100045）（2.華北電力科學研究院有限責任公司 北京 100045）（3.深圳市科陸智慧工業有限公司 深圳 518057）

1 引言

電力負荷預測是制定發電計劃和電力系統發展規劃的基礎，精確的負荷預測對于電力系統經濟、安全、可靠地運行具有重要意義［1］對電力系統短期負荷預測方法的探索，一直是國內外學者關注的一個熱點，多年來已經提出了許多預測方法，如時間序列預測法［2］，神經網絡預測法［3］，組合模型預測法［4］，取得了很多卓有成效的進展。目前已有的預測模型都是針對全部用戶的負荷值進行預測［5～7］，并未考慮到不同用戶的用電類型對負荷結果的影響。

本文針對城市電力負荷預測中存在的行業類型多，不同行業用戶乃至同一行業不同用戶用電負荷差異大，大量的用戶無明確的行業類型特征，城市不同時刻電力負荷差別大等問題，設計智能電表計量自動化系統采集計量點數據，開展基于用戶分群策略研究的電力實時負荷研究，提出了聚類算法與回歸算法結合的預測方法，對城市實時電力負荷預測具有一定的指導意義。

2 智能電表計量設計

2.1 系統概述

在實驗中，設計智能電表計量自動化系統采集計量點數據在進行負荷預測時，采用先對用戶進行細分，再分別進行預測的方法。即先對用戶按照負荷特性進行分類，計算合適的用戶聚類簇數，利用聚類算法將用戶分為不同用電特征的幾大類，然后對各分群分別采用回歸算法進行負荷建模與預測，再將各個群組的預測結果進行累加求和，形成最終的城市負荷預測。另外還可以將實際預測結果與歷史實際數據進行對比，對預測結果評價，并反饋至預測模型，通過調整建模參數，提升預測模型精度，具體流程如圖1所示。

2.2 計量自動化系統

某供電局的智能電表計量自動化系統采集的計量點數據主要包括：通信流量數據、表碼數據和瞬時量數據。通信流量數據包含終端編碼、數據日期、發送（下行）字節、接收（上行）字節、重連次數、數據流量、報警流量、心跳流量、在線時間等終端與主站之間的通信流量數據。表碼數據［8］包含正向有功表碼、反向有功表碼、正向無功表碼、反向無功表碼等用戶累計用電信息。瞬時量數據［9］包含有功功率、電流、電壓等用戶實時的用電信息。

本論文以某供電局2016年12月份的計量自動化系統采集的58995個大客戶的瞬時量數據作為實驗對象，以用戶實時功率數據為基礎，研究電力用戶的分群策略，尋找在分群效果穩定的數據簇數目的確定方法，并在此基礎上，使用局部加權線性回歸算法，對每一類用戶進行負荷預測，并形成最后所有用戶的負荷。瞬時量數據表各字段屬性如表1所示。

3 電力用戶分群策略

為了精確描述電力負荷隨時間變化的規律，分析各種因素對電力負荷特性的影響程度，找出不同行業用戶具備的相同的用電模式，本文選取供電局提供的大客戶的連續4周的整點時刻的數據的均值作為該客戶每個小時的負荷值，以0點到23點共24個整點時刻的負荷作為聚類的維度，利用K-means算法［10］進行聚類，分析各用戶的負荷波動指標。

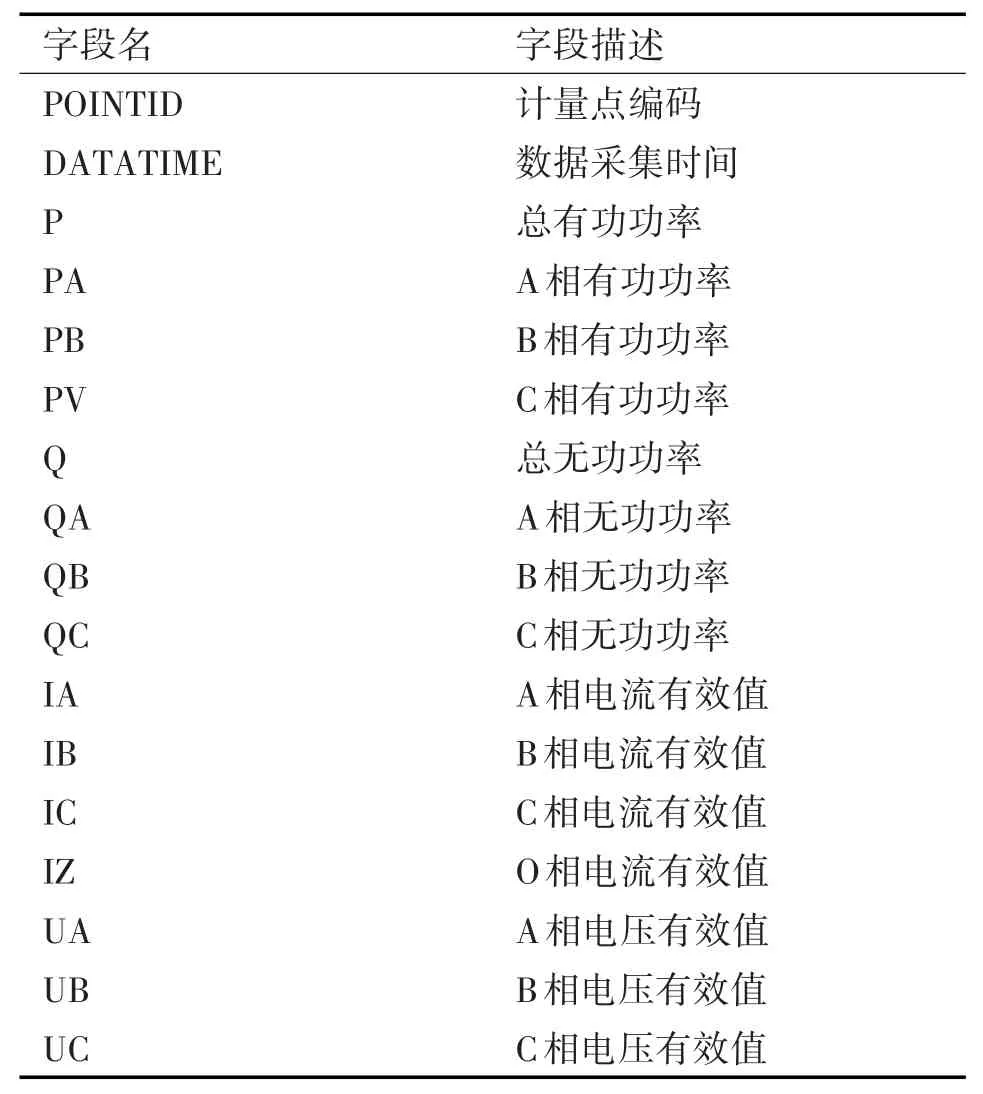
表1 瞬時量字段表

將歸一化的用戶負荷均值數據利用K-means聚類算法在24個時間點維度上進行聚類，從而將所有行業每個用戶的所有計量點按照負荷波動指標進行分類，最終得出每個用戶所屬的用電負荷類別。

3.1 數據預處理與特征提取

不同時刻的用電負荷的差值很大，例如白天工廠的用電負荷遠遠大于凌晨時刻的用電負荷。如果直接聚類，數據點距離會偏向于負荷值較大的時間維度影響，從而掩蓋其他時間維度的數據特征，導致聚類結果不準確。所以需要對24個時間特征維度進行數值歸一化處理，將所有的特征指標維度縮放到同一尺度內。

實驗中采用z-score標準化（zero-mean normal?ization）方法［11］，計算時對每個特征分別進行，如式（1）所示：

其中，μ和σ分別代表數據集某特征列的均值和標準差，經過該方法歸一化的數據屬性的均值為0，標準差為1。將每個用戶、每個維度歸一化之后的24個小時點的負荷均值作為該用戶的聚類維度，如表2的例子所示。

上述的例子中，F1是第一個特征維度，表示歸一化后0點時刻的負荷值，該用戶原始負荷值為3244.194kW，0點時刻所有用戶的負荷均值為3936.549kW，負荷標準差為4212.466kW，故由（3244.194-3946.549）/4212.466得到該用戶0點時刻的歸一化負荷值。

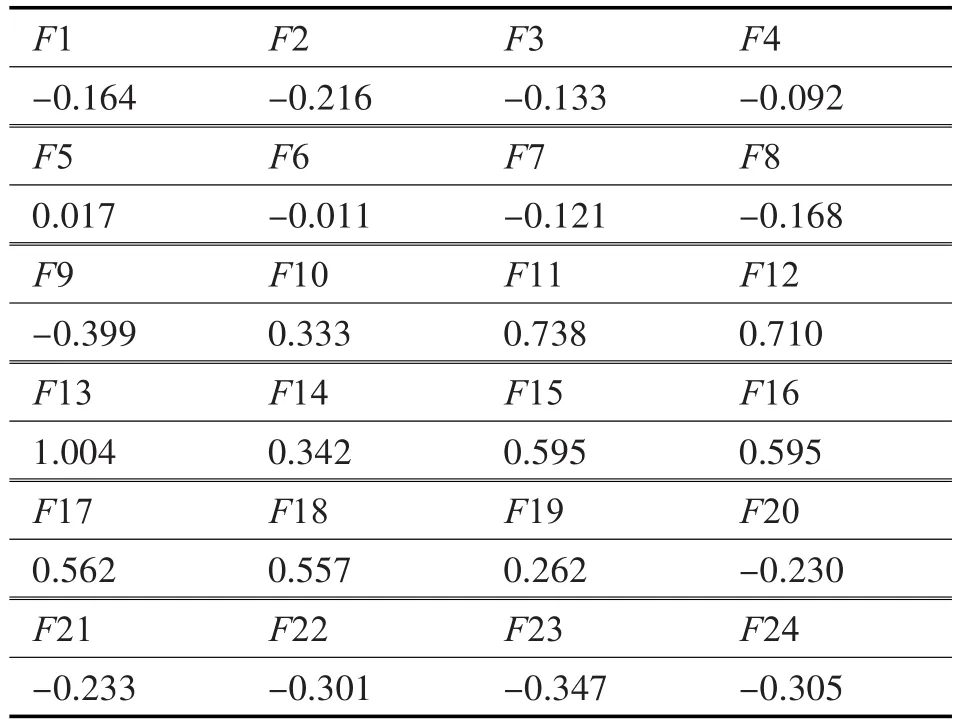
表2 聚類特征選取例子

3.2 聚類簇數K的確定方法

K-means是一種將給定數據集劃分為K個數據簇的算法。需要劃分的簇的數量是需要提前指定的，簇的中心是在該簇中的所有數據的質心（本文采用均值計算），由簇的中心來描述這個簇。算法運行前需要指定簇的數目K及收斂條件。

一種用于度量聚類效果的指標是SSE（Sum of Squared Error，誤差平方和）［12］，即計算聚類穩定后的所有數據點距離其所屬數據簇的中心的距離的總和，SSE值越小表示數據點越接近于它們的質心，聚類效果也越好。因為對誤差去了平方，因此更加重視那些遠離中心的點，可以通過遍歷所有質心并計算點到每個質心的距離來完成，如式（2）所示。

其中，表示第i條訓練數據的第 j個特征，表示第i個訓練數據所屬聚類質心的第 j維特征。

為確定對數據集合適的K的選取，實驗中令K從1（將所有的用戶歸到一個數據簇）到K為43（因為K-means一般作為數據預處理，或者用戶輔助分類給數據添加標簽，同時在實驗室中發現隨著K的增加，聚類誤差的變化已經接近于0，所以K的設置一般不會很大），在每個K值上重復運行數次K-means（避免局部最優解）并計算當前K取值的誤差平方和［13］，如圖2所示。

圖2中，X軸表示聚類數據簇K的取值，左側Y軸的圖例表示聚類結果的誤差平方和，對應圖中的三角形圖標的線條，右側Y軸的圖例表示誤差平方和的梯度。

從圖2可以看出，當K取值為14的時候，聚類效果的誤差平方和已經接近于水平軸，同時負荷差值的梯度在0附近波動，表明即使增加K的取值對聚類效果的誤差不會產生太大的影響，故選定14作為用戶分類的數據簇的數目。

4 局部加權線性回歸的實時負荷趨勢預測

基于上述的用戶分群策略，將用戶依據其用電模式，將其劃分到不同用戶組，接下來需要針對每一類用戶使用局部加權線性回歸算法［14］，使用歷史負荷數據作為模型特征，預測未來某一天每個小時的負荷值，設計準確性評價指標，將其與真實的負荷值進行比對，驗證模型的有效性。

考慮到局部加權線性回歸算法優越的運算性能和大量用戶負荷的規律性，實驗采用局部加權線性回歸分析方法。局部加權線性回歸算法只要求幾個簡單的特征就能快速地預測出曲線的趨勢，實驗中將其與線性SVR算法［15］進行比對，實驗結果表明局部線性回歸算法在實時電量負荷預測方面非常有效。

4.1 數據預處理簡介

通過上述的聚類，將用戶數據聚為14類數據簇，每一類均包含大量的計量點。在負荷預測的數據預處理階段，需將每一個數據簇中的計量點的負荷值按照整點時間疊加，得到該數據簇中所有的計量點的整點時刻的負荷總和，并按照時間排序。

為預測未來某一個時間點的負荷，將該時間點之前連續幾天的負荷數據作為其特征，數據構造如下表所示，以8天共192維的數據作為特征的維度。

表3 回歸特征選取

預測某一天每個整點時刻的負荷值均從當天零點時刻的負荷著手預測，并將預測出來的負荷與之前的195維的數據組成新的訓練樣本，以滑動窗口的形式預測下一個時間點的負荷，不斷往復，直到預測出最后一個時間點的負荷，從而將當天所有時間點的負荷預測出來。

為確保仿真結果的準確性，選取12月份最后一周的數據作為驗證數據集進行7次交叉驗證，每次預測一天24個小時的負荷，并以7天的預測準確性的均值作為最后的實驗結果。

4.2 局部加權線性回歸算法介紹

局部加權線性回歸（Logically Weighted Linear Regression，LWLR）是對線性回歸的拓展，主要思路是給待預測點附近的每一個點賦予一定的權重，然后在這個子集上基于最小均方差來進行普通的回歸，其目標函數是加權的最小二乘：

其中，ω是權值，其作用在于根據要預測的點與數據集中的點的距離來為數據集中的點賦權值，當某一點距離待預測的點較遠時，其權重較小，否則較大。

4.3 準確性評價指標

因為每次模型均預測一個時間點的負荷值，需要評價的是預測負荷與真實負荷的差距，故實驗采用如下的數據準確性評價指標：

其中，Testvalue表示真實負荷值，Predictvalue表示預測負荷值，通過上述公式計算預測值與真實值之間的擬合程度。

5 實驗結果分析

5.1 特征維度的確定

在上述的數據預處理階段，為預測某時刻的負荷值，將該時刻之前的負荷值作為模型的特征，為確定合適的特征數目，以1天（24個數據點）的數據到14天（336個數據點）的數據作為模型特征，分別計算線性回歸和線性SVR的準確性，結果如圖3所示。

由圖3可以看出，當選取的數據特征在10天以內時，線性回歸的準確率高于SVR，同時，當特征選取為8天（192維）的時候，兩種方法均達到最高的準確性，故選用8天共192維數據作為負荷預測的特征數據。

5.2 各個整點時刻的負荷預測準確性評價

以8天共196維的負荷值作為預測模型的特征，以上述的負荷預測模型使用滑動窗口方法分別預測12月25日～12月31日所有時間點的負荷值，并按照時間點疊加求7天的均值，計算模型對每個時刻的預測準確性，結果如圖4所示。

從上圖可以看出，在絕大多數的時間點上，線性回歸模型的預測準確性均大于SVR，同時預測值均在97%以上，模型預測準確性較高，具有一定的實用價值。

以8天共196維的負荷值作為預測模型的特征，以上述的局部加權線性回歸預測模型預測12月30日（周五）當天每個整點時刻的負荷值，如下圖所示圖5基于LWLR的12月30日的整點時刻負荷預測結果

從圖5可以看出，局部加權線性回歸算法的預測值與原始負荷值基本匹配，由于使用前一個預測值加入訓練數據來預測下一個時間點，隨著誤差的累計，后面的時間點較前面的時間點有更大的誤差。

6 結語

采用某供電局的智能電表計量自動化系統采集到的用戶負荷數據，基于K-means聚類算法和線性回歸算法構建了基于用戶分群研究的智能電表計量電力負荷預測模型，實驗結果證明了該混合算法能依據歷史負荷信息有效地對預測當天每個時刻的負荷進行準確性的預測，表明在智能電網的負荷預測上，利用智能電表計量自動化的數據挖掘理論是一種有效的嘗試。

［1］王保義，趙碩，張少敏.基于云計算和極限學習機的分布式電力負荷預測算法［J］.電網技術，2014，38（02）：526-531.

［2］侯海良，孫妙平，蔡斌軍.基于RBF-ARX模型的短期電力負荷預測［J］.河海大學學報（自然科學版），2015，43（03）：271-277.

［3］金鑫，李龍威，季佳男，等.基于大數據和優化神經網絡短期電力負荷預測［J］.通信學報，2016，37（1）：36-42.

［4］蘇士美，王明霞，姚猛，等.基于WHAC-E組合預測模型的短期電力負荷預測［J］.鄭州大學學報（工學版），2014，35（03）：86-89.

［5］肖白，周潮，穆鋼.空間電力負荷預測方法綜述與展望［J］.中國電機工程學報，2013，33（25）：78-92，14.

［6］肖勇，楊勁鋒，馬千里，等.基于模塊化回聲狀態網絡的實時電力負荷預測［J］.電網技術，2015，39（03）：804-809.

［7］崔和瑞，彭旭.基于ARIMAX模型的夏季短期電力負荷預 測［J］.電 力 系 統 保 護 與 控 制 ，2015，43（04）：108-114.

［8］劉慶.電力營銷系統自動化抄表問題探討［J］.通訊世界，2014（17）：20-21.

［9］Kavousian A，Rajagopal R，Fischer M.Determinants of residential electricity consumption：Using smart meter da?ta to examine the effect of climate，building characteris?tics，appliance stock，and occupants'behavior［J］.Ener?gy，2013（55）：184-194.

［10］趙莉，候興哲，胡君，等.基于改進k-means算法的海量智能用電數據分析［J］.電網技術，2014，38（10）：2715-2720.

［11］曲朝陽，陳帥，楊帆，等.基于云計算技術的電力大數據預處理屬性約簡方法［J］.電力系統自動化，2014，38（08）：67-71.

［12］成衛青，盧艷紅.一種基于最大最小距離和SSE的自適應聚類算法［J］.南京郵電大學學報（自然科學版），2015，35（02）：102-107.

［13］張斌，莊池杰，胡軍，等.結合降維技術的電力負荷曲線集成聚類算法［J］.中國電機工程學報，2015，35（15）：3741-3749.

［14］張素香，趙丙鎮，王風雨，等.海量數據下的電力負荷短期預測［J］.中國電機工程學報，2015，35（01）：37-42.

［15］Hong W C，Dong Y，Zhang W Y，et al.Cyclic electric load forecasting by seasonal SVR with chaotic genetic al?gorithm［J］.International Journal of Electrical Power&Energy Systems，2013，44（1）：604-614.