無刷直流電機的反演自適應動態滑模控制

苗敬利 井爽

摘 要： 無刷直流電機在工作中容易受到系統的外部干擾和參數攝動的影響，根據滑模變結構具有快速響應、魯棒性好、物理實現簡單等優點，可以將滑模變結構控制應用于無刷直流電機中。為了有效地降低無刷直流電機的抖振現象，提出動態滑模方案。同時將自適應技術和反演控制相結合運用到動態滑模方案中，可以實現不確定系統的無抖振滑模控制。仿真結果證明了兩種方案的正確性。

關鍵詞： 無刷直流電機； 反演自適應； 動態滑模； 動態切換函數； 抖振； 滑模變結構

中圖分類號： TN876?34； TM3 文獻標識碼： A 文章編號： 1004?373X（2018）13?0119?04

Abstract： The brushless DC motor in working is easily influenced by external disturbance and parameter perturbation of the system. Since the sliding mode variable structure has the advantages of fast response speed， high robustness and simple physical implementation， the sliding mode variable structure control can be applied to the brushless DC motor. A dynamic sliding mode scheme is proposed to reduce the buffeting of the brushless DC motor effectively. The adaptive technology and backstepping control are combined， and used to the dynamic sliding mode scheme， which can realize the sliding mode control without buffeting for the uncertain system. The simulation results show that the two schemes are correct.

Keywords： brushless DC motor； backstepping adaptive technology； dynamic sliding mode； dynamic switching function； buffeting； sliding mode variable structure

0 引 言

無刷直流電機（Brushless DC Motor，BLDCM）具有效率高、響應快、轉矩大和慣性低等優點，已經在各個領域中廣泛應用[1?3]。理想的電機調速系統應具有高精度的穩態、快速度的響應、較強的抗干擾能力等特點，因此需要高性能的控制策略[4?5]。

由于滑模變結構具有響應速度快、魯棒性好、物理實現簡單等優點，因此得到了廣泛應用。滑模控制也驗證了其性能。但是，本質上滑模變結構控制在開關特性不連續的情況下將會引起系統出現抖振現象，所謂抖振就是在光滑的切換面上疊加了一種波動的軌跡[6]。抖振文獻[7]在無刷直流電機的調速系統中應用了趨近率法的滑模變結構，不僅有效抑制了超調量，而且響應速度快，并具有很好的魯棒性。文獻[8]在無位置傳感器的BLDCM控制系統中應用了滑模變結構既對系統控制的準確性產生一定的影響，又會加大能量的消耗，從而破壞系統的性能，甚至使系統產生振蕩或者損壞控制器部件[2]。而文獻[9]將模糊控制與滑模控制相結合，僅僅改善了系統的抖振。

為了能夠有效地削弱滑模控制的高頻抖動現象，使用動態滑模控制，同時將自適應技術與反演控制方法相結合，通過設計新的切換函數，采用動態滑模控制算法可以實現不確定系統的無抖振滑模控制。

1 無刷直流電機數學模型[10]

電機相電壓方程式如下：

4 系統仿真與分析

采用Matlab/Simulink工具對無刷直流電機控制系統建立仿真模型，并分別對動態滑模控制算法和反演自適應動態滑模控制算法進行仿真試驗，同時驗證這兩種控制算法的有效性和可行性。仿真中所用無刷直流電機的系統參數設置為：阻尼系數[B=]0.000 2 N·m·s/rad，極對數[np=1]，定子繞組電阻[R=1] Ω，針對無刷直流電機中的[J]和[B]的值對應于一階系統中 [θ=0.12]，轉動慣量[J=0.05] kg·m2，無刷直流電機的轉速[ω]的初始值為0對應于一階系統中[x（0）=0]。反演自適應動態滑模控制器的參數為：[c1=2]，[θ1]和[θ2]的初始值取[0 0]，電機空載啟動，進入穩態后[t=]0.2 s，外加負載信號[TL=]1 N·m。

為了驗證本文設計的控制器的控制效果，把該控制器與傳統的PID控制器分別用在無刷直流電機的模型中進行仿真控制，所用的PID控制器的參數定為：[Kp=5]，[Kd=0.001]，[Ki=0.01]。假定給定轉速為1 250 r/min，在三種控制算法下所得響應曲線如圖1～圖3所示。

比較圖1和圖3可知，動態滑模控制算法相比于PID控制算法，跟蹤速度快，超調量變小，有限地降低了抖振，從而證明動態切換函數滑模控制具有可行性。

比較圖2和圖3可知，反演自適應動態控制算法相比于PID控制算法，快速跟蹤，并且超調量也更小，并且在負載突然改變時轉速沒有明顯的變化，因此證明反演自適應動態控制比PID具有更好的可行性和穩定性。

通過比較圖1，圖2可以看出反演自適應動態滑模控制算法的響應速度快，在負載突變的時候，轉速沒有明顯的變化。動態滑模控制算法剛開始響應速度慢。在負載突變的時候，轉速有點變化。反演自適應動態滑模控制的消抖能力強，魯棒性強，對過程參數的變化以及對未建模部分的動態過程不敏感。因此在負載突然改變時轉速沒有明顯的變化。

由于運行過程中電機的溫升會增大，繞組的電阻也會增加，這些因素都會影響電機的參數。比如定子繞組的電阻增大20%，即[R=]1.2 Ω時，電機應用反演自適應動態滑模控制算法時相應轉速響應曲線如圖4所示。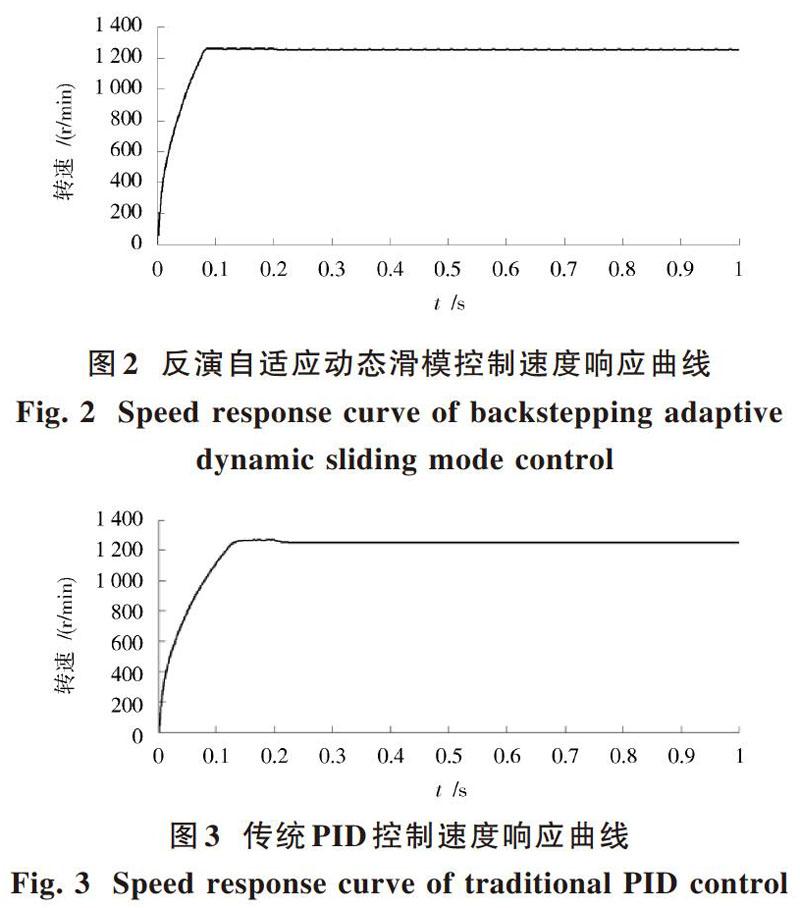

由圖2和圖4可知，當電阻增大時，電機應用反演自適應動態滑模控制算法的轉速響應曲線基本沒有發生變化，說明電機

參數的變化對這兩種控制算法影響不大，反演自適應動態滑模控制算法都具有較好的魯棒性。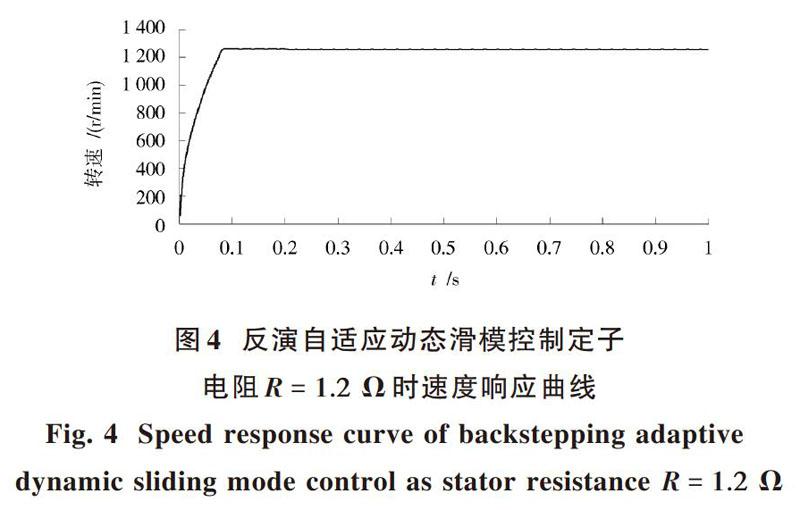

5 結 論

本文利用Matlab/Simulink對無刷直流電機控制系統進行控制算法仿真實驗分析，分別得到了反演自適應動態控制的仿真圖形和動態滑模控制算法仿真圖形，將這兩種控制算法分別與PID控制算法相比較，證明了這兩種控制算法可以快速跟蹤減小超調量。但是將反演自適應動態滑模控制算法與動態切換函數滑模控制算法相比較，發現反演自適應動態滑模控制算法具有較快的響應速度，能更有效地消除抖振現象。也得出反演自適應動態滑模控制算法能夠使整個閉環系統具有更好的魯棒性。

參考文獻

[1] 張勇，程小華.改進的BLDCM直接轉矩控制系統仿真研究[J].計算機仿真，2014，31（1）：323?327.

ZHANG Yong， CHENG Xiaohua. Improvement of BLDCM direct torque control system simulation [J]. Computer simulation， 2014， 31（1）： 323?327.

[2] BORA T C， COELHO L D S， LEBENSZTAJN L. Bat?inspired optimization approach for the brushless DC wheel motor problem [J]. IEEE transactions on magnetics， 2012， 48（2）： 947?950.

[3] 李宏，王崇武.永磁無刷直流電機模糊自適應控制器設計[J].計算機仿真，2011，28（2）：209?212.

LI Hong， WANG Chongwu. Permanent magnet brushless DC motor fuzzy adaptive controller design [J]. Computer simulation， 2011， 28（2）： 209?212.

[4] 夏長亮，方紅偉.永磁無刷直流電機及其控制[J].電工技術學報，2012，27（3）：25?34.

XIA Changliang， FANG Hongwei. Permanent magnet brushless DC motor and its control [J]. Transactions of China electrotechnical society， 2012， 27（3）： 25?34.

[5] 楊孝敬，林青松.基于PSD的多電機速度伺服驅動控制研究[J].計算機測量與控制，2013，21（11）：2994?2996.

YANG Xiaojing， LIN Qingsong. Research on multi?motor speed servo control based on PSD [J]. Computer measurement and control， 2013， 21（11）： 2994?2996.

[6] 李林杰，焦振宏，時建欣.基于滑模變結構控制的對轉無刷直流電機調速系統[J].微特電機，2010，38（10）：44?47.

LI Linjie， JIAO Zhenhong， SHI Jianxin. Contrarotating brushless DC motor speed control system based on sliding mode variable structure control [J]. Micro & special motor， 2010， 38（10）： 44?47.

[7] LONG B， ZHOU H B， CAO B G， et al. Position tracking controlling system of sensorless BLDCM by using MRAC [C]// 2007 IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications. [S.l.]： IEEE， 2007： 1?5.

[8] 李春華，孫約，羅琦.非線性系統的反演自適應動態滑模控制[J].計算機工程與設計，2009，30（1）：185?187.

LI Chunhua， SUN Yue， LUO Qi. The inversion adaptive dynamic sliding mode control of nonlinear system [J]. Computer engineering and design， 2009， 30（1）： 185?187.

[9] SONG H， YU Y， YANG M， et al. A novel SMC?fuzzy speed controller for permanent magnet brushless DC motor [C]// The Eighteenth IEEE Applied Power Electronics Conference and Exposition. [S.l.]： IEEE， 2003： 281?285.

[10] 苗敬利，鄒靖.基于動態Terminal滑模控制的無刷直流電機系統研究[J].制造業自動化，2014，36（11）：61?64.

MIAO Jingli， ZOU Jing. Research about a system of the brushless DC motor based on dynamic terminal sliding mode control [J]. Manfacturing automation， 2014， 36（11）： 61?64.

[11] 劉金琨.滑模變結構控制Matlab仿真[M].北京：清華大學出版社，2015.

LIU Jinkun. Matlab simulation for sliding mode control [M]. Beijing： Tsinghua University Press， 2015.