空壓機轉子系統碰摩故障仿真分析*

吳　桃，常錫振

(1.常州鐵道高等職業技術學校，江蘇 常州　213011； 2.江蘇天麒工業環境科技有限公司，江蘇 常州　213000)

0　引　言

轉子系統作為旋轉機械的核心部件，常常出現各種單一或耦合的振動故障，研究這些故障對轉子系統的影響，對及時發現并處理這些故障有著重要的意義[1]。以有限元和轉子動力學相關理論為基礎建立了轉子系統的有限元動力學模型，并驗證了模型的正確性，以此為基礎對轉子系統碰摩故障進行了分析。

1　轉子系統的動力學模型

1.1　轉子有限元模型建立

轉子系統由一些離散的葉輪、具有分布質量及彈性的軸段和軸承座等部件組成，將系統離散成由剛性圓盤、軸段等單元連接成的模型，各個單元間在節點處聯接，忽略轉子系統的軸向變形[2]。彈性軸段單元的廣義坐標分別為兩端節點的位移的轉角，如圖1所示。

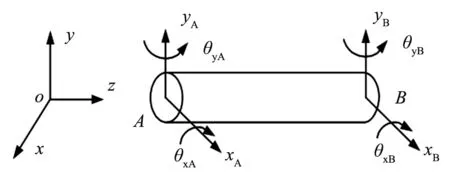
圖1　軸段單元的有限元模型

其復數表示為：

μ=[xA-jyAθyA+jθxAxB-jyBθyB+jθxB

(1)

將多跨轉子系統離散成具有N個節點、N-1個由剛性圓盤、彈性軸段和軸承支承的有限元動力學模型，其整體動力學方程為：

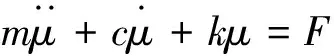
(2)

其中：M為整體質量矩陣；C=D+ωG；D為整體阻尼矩陣；G為陀螺力矩矩陣；ω為轉子轉速；K為整體剛度矩陣；矩陣為2N×2N階對角方陣，具體形式參見文獻[3]。

空壓機軸模型如圖2所示，將該轉子系統離散成具有29個節點有限元動力學模型、其中共有28個彈性軸段單元，在葉盤和葉輪位置處，將葉盤和葉輪等效為剛性圓盤[4]，加在節點12～19、21、22處，軸承支承假設為等剛度彈性軸承，軸承剛度為k=108N/m，加載位置為9、10、22、23號節點。……