有趣的搭配

倪艷

小朋友，我們在生話中經常遇到簡單的搭配和排列問題，下面讓我們一起來探索其中的規律，尋找解決這糞問題的方法。

例1.學校要在3名男生和4名女生中挑選男、女節目主持人各一名，挑選的結果會出現多少種可能？

我是這樣解的

可以用字母A1、A2、A3表示3名男生，用B1、B2、B3、B4表示4名女生，用連線的方法尋找問題的答案：

從圖中可以看出，先挑選好1名男主持人，再挑選女主持人，挑選的結果就會有4種可能；因為有3名男主持人，所以挑選的結果就有3個4種不同的可能，也就是3×4=12（種）可能。

例2.一列客車在蘇州、南京之間往返行駛，中間停靠常州、鎮江，每兩地之間的距離都不相同，鐵路局要印幾種火車票？

我是這樣解的

先畫示意圖（如下圖），從圖中可以看出，從蘇州“往”南京，要印火車票3 +2 +1=6（種）。由于“往”和“返”的火車票的始發站和終點站是不同的，例如從蘇州去常州與從常州回蘇州，雖然票價相同，但卻是兩種不同的火車票，因此要印的火車票是（3+2+1）x2=12（種）。

例3.用1、2、3、4這四個數字可以組成多少個沒有重復數字的三位數？

我是這樣解的

按從小到大的順序思考，百位上是1的三位數有：123、124、132、134、142、143，共6個；百位上是2的三位數有：213、214、231、234、241、243，也是6個；同樣，百位上是3和4的三位數也各有6個，因此，一共有6×4=24（個）。

例4.一個骰子的六個面分別寫有1-6，如果用兩個骰子同時擲（如下圖），朝上的兩個數相加，一共會出現幾種不同的和？和最大是多少？最小是多少？

我是這樣解的

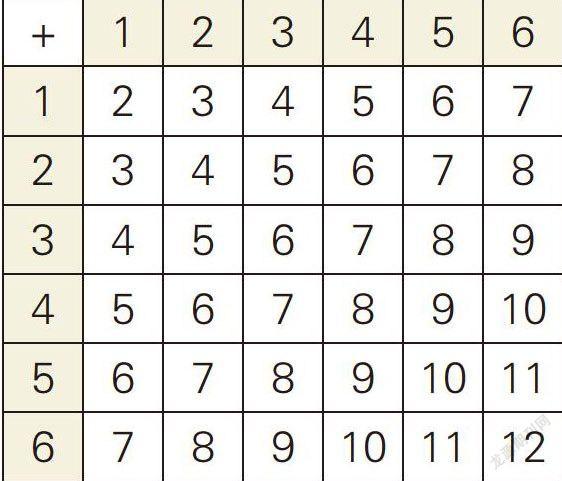
可以分步思考，即先確定第1個骰子朝上的數依次為1、2、3、4、5、6，然后依次加上第2個骰子朝上的數，列表如下：