基于卡爾曼濾波的快時變稀疏信道估計新技術
袁偉娜, 王嘉璇
(華東理工大學信息科學與工程學院, 上海 200237)
OFDM (orthogonal frequency division multiple-xing)技術具有高頻譜利用率和抗多徑干擾能力,目前在3GPP(3rd generation partnership project)、4G LTE (long term evolution)等多種無線通信標準中得到了廣泛應用.隨著無線通信技術的發展,人們對許多從前未被重視的應用場景下的通信質量需求提高,比如:信道具有稀疏特性的偏遠空曠的郊外山區,或信道具有快速變化的高速鐵路等場景.信道估計的性能是衡量通信系統性能的主要標準,因此對于復雜多樣化信道估計技術的研究具有重要的意義[1-3].
在郊區山區等呈現稀疏特性的信道環境下,信道多徑時延分布是零散的,即由幾個具有明顯響應的主徑,以及大部分低于一定閾值近似為0的徑組成.如果仍假設主徑連續集中在前幾徑,誤差將大大增加,而如果對最大時延內所有徑數進行估計,估計數量也將增加.壓縮感知(compress sensing, CS)的提出對稀疏信道估計問題提供了很大的幫助,文獻[4-6]基于CS算法分別研究了單天線和多天線OFDM系統時不變稀疏信道估計,文獻[7-9]基于CS算法和傳統估計算法研究了時變稀疏信道估計,文獻[10]采用卡爾曼濾波算法(Kalman filter, KF)與CS相結合的算法研究慢時變稀疏信道估計,此處的慢時變指單個符號內信道響應不變而相鄰符號間是變化的,該算法不適合用于快時變信道的估計.
在高鐵等信道環境中,由于多普勒效應的存在,信道在一個符號周期內快速變化,稱其為快時變信道,此時,待估計的信道參數數量大大增加.文獻[11-12]采用基擴展模型(basic expansion model, BEM)對每一個OFDM符號塊對應的快時變信道建模,該模型可以對快時變信道特性進行較好的擬合,同時也可以降低估計參數數量,然后采用LS(least square)、 LMMSE(linear minimum mean square error)和ML(maximum likelihood)對BEM系數進行估計,沒有考慮相鄰符號塊間信道參數的關系.文獻[13]考慮了相鄰符號塊信道參數的關系,采用KF算法對相鄰符號對應的BEM信道模型系數進行估計,從而獲得信道估計,但研究的是非稀疏信道,將該算法應用于稀疏信道估計時,性能較差.目前,尚未查閱到考慮相鄰符號塊間信道參數關系的快時變且稀疏的信道估計算法.
本文提出一種新的快時變稀疏信道估計方法.該方法基于快時變稀疏信道的BEM模型,采用CS算法進行主徑估計,再結合KF算法估計BEM系數,進而獲得信道估計值.同時,實驗仿真表明,本文提出的方法有效地減小了信道估計的誤差.
1 基于BEM的快時變信道模型
OFDM系統的時域接收信號模型為
(1)
式中:x、y分別為發送與接收的OFDM符號;
h(n,l)為一個OFDM符號周期內第l徑第n個采樣點的信道響應;
N為一個符號周期總采樣點數;
(·)N表示模為N的循環移位;
L為最大時延內總徑數;
w(n)是第n個采樣點的均值為0、方差為σ2的加性高斯白噪.
BEM采用一組基函數的線性組合,可以較好地擬合快時變信道的信道響應,表示如式(2).
(2)
式中:n=0,1,…,N-1;
l=0,1,…,L-1;
bq(n)、gq(l)和Q分別為BEM的基函數、系數和階數.
通常假定在一個OFDM符號內,BEM系數保持不變,而基函數是一組固定的正交基,因此采用BEM可以將待估計的信道參數由NL個降到(Q+1)L個,大大減少了估計數量.得到BEM系數估計值后,再經過BEM模型即可獲得信道響應.
常用的BEM基函數有:復指數基擴展模型(complex exponential BEM, CE-BEM)、過采樣復指數基擴展模型(generalized complex exponential BEM, GCE-BEM)、多項式基擴展模型(polynomial BEM, P-BEM)、離散卡-洛基擴展模型(discreteKarhuen-loève BEM, DKL-BEM)和離散橢圓基擴展模型(discrete prolate spheroidal BEM, DPS-BEM).
式(2)寫成矩陣形式為
(3)
式中:bq=(bq(0),bq(1),…,bq(N-1))T;
Gq為N×N維的Toeplitz循環矩陣;
h為N×N維的時域信道矩陣.
Gq和h表示如式(4)~(5).
(4)
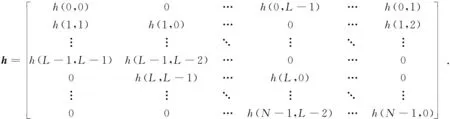
(5)
式(1)寫成矩陣形式為
y=hx+w,
(6)
式中:y=(y(0),y(1),…,y(N-1))T;
x=(x(0),x(1),…,x(N-1))T;
w=(w(0),w(1),…,w(N-1))T.
則相應的頻域接收信號為
Y=FhFHX+W=HX+W,
(7)
式中:Y=Fy;
X為OFDM符號,
X=(FH)-1x;
F為N點傅里葉變換矩陣,
F=(Fij),i,j=0,1,…,N-1,
H為一個N×N大小的頻域信道矩陣;
W為頻域的噪聲.
將式(3)代入后可表示為
Y=FhFHX+W=
(8)
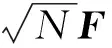
gq=(gq(0),gq(1),…,gq(L-1))T.
令A=Fdiag(bq)FH,式(8)可以表示為
(9)
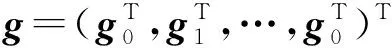
Y=AΔg+W,
(10)
再令S=AΔ,則頻域接收信號最終可表示為
Y=Sg+W.
(11)
基于梳狀導頻輔助的估計方法,式(7)中導頻處的接收信號可表示為
YP=SPgP+Sdgd+WP,
(12)
式中:WP為導頻處的噪聲;
SPgP為有效接收數據,p=1,2,…,P,P∈N;
Sdgd為數據子載波對導頻子載波的干擾,令d=Sdgd,則有
YP=SPgP+d+WP.
(13)
2 基于壓縮感知的稀疏信道時延估計
在稀疏信道的環境下,不需要完整地估計最大時延內所有徑數的增益,只需對有明顯增益的主要時延處Ldelay徑進行估計.因此,要在信道增益估計前先在L中找出主徑的位置Ldelay.
壓縮感知理論的提出,給處理稀疏信號提供了一種思路.壓縮感知是一種在稀疏條件下尋找欠定線性系統解的算法,可以用低于奈奎斯特采樣頻率去高度重建信號.對于一個未知的信號X∈CN,X中只有K個非零元素(K?N),即信號X的稀疏度為K.選擇一個觀測矩陣Φ∈CM×N對X進行測量,觀測過程表示為
Y=ΦX+V,
(14)
式中:V為噪聲.
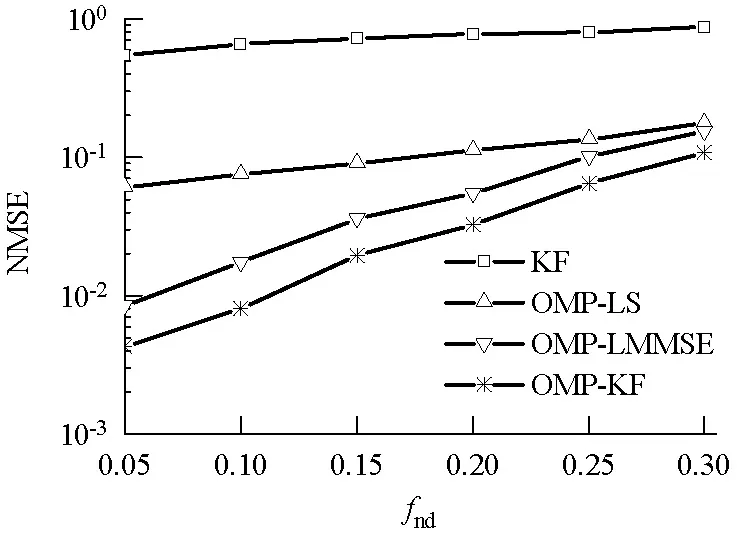
得到觀測信號Y∈CM,其中M 正交匹配追蹤(orthogonal matching pursuit, OMP)[14]算法是一種常見的基于貪婪迭代的壓縮感知重構算法,其基本思想是初始化殘差跟原始索引集,每次迭代通過計算內積,不斷地找到與殘差相關度最高的原子,并更新索引集,最后逐步逼近系數向量.利用OMP進行時延估計的過程如下: 步驟1初始化索引集T0=?. 步驟2計算 式中:φt為Φ中的列; Γλ為Φ中所有列數. 步驟3更新索引集 Tn={Tn-1,φt}, LS估計 步驟4計算殘差 rn=Y-TnXn, 并更新 步驟5重復步驟3、4,直到殘差小于閾值或Tn的列數達到設定值K. 為了在稀疏信道估計中應用上述理論,需要構建稀疏信號和觀測矩陣.假設發送端的所有導頻信號為XP,則對應位置的接收端信號YP表示為 YP=HPXP+WP, (15) 式中:XP、YP均為NP×1維向量; WP為NP×1維導頻處噪聲; HP為NP×NP維頻域信道響應,其對角元素為第p個導頻位置處的頻響,表示為 (16) 又由于導頻處的多徑信道頻響表示為 (17) Pp為第p個導頻在子載波中對應的位置. 在快時變環境下,每徑信道響應在1個符號周期內每個采樣點處都不同,但其平均值也可以表示總體的稀疏性.則可將1個符號周期內所有導頻符號處對應的頻響表示為 (18) 式中:HP=(H0,H1,…,HNP-1)T; Φ=(Φpl), 建立好上述快時變稀疏信道模型后,可應用信道估計算法對BEM系數g進行估計.傳統的信道估計算法通常為LS和LMMSE. (19) 則可解得g的LS估計值為 (20) LS算法不需要信道和噪聲的統計信息,因而復雜度較低.但同時也限制了性能的進一步提升,在干擾比較大或是信噪比較差的時候,信道估計的性能可能不夠理想. (21) 則可解得LMMSE估計值為 (22) 式中:Rg、Rd和RW分別為BEM系數、發送數據和噪聲的自相關矩陣. LMMSE算法考慮了噪聲和信道的統計信息,因此性能優于LS.但同時復雜度也較高,而且要獲取信道的統計信息也非常困難,如果得到的統計信息和實際信道不匹配,將會帶來較大的誤差.通常采用特定的信道,如本文采用的是Jakes模型信道[15],以方便計算信道的統計信息. 上述方法(LS或LMMSE)均是在對每一個OFDM符號塊對應的信道參數分別進行BEM建模的基礎上進行估計的,相鄰符號塊的參數之間并無相關.然而,在實際情況中,相鄰OFDM符號之間對應的信道參數是隨時間平滑漸進變化的[13].因此,考慮到這種情況,可以用自回歸(autoregression, AR)模型[16]來描述和刻畫相鄰符號間對應的信道增益的這種動態變化,為了降低復雜度,這里選用一階AR模型,如式(23). hml=Ahlh(m-1)l+uml, (23) 式中:hml為第m個OFDM符號第l徑的信道響應向量; Ahl為信道系數的狀態轉移矩陣; uml為模型誤差,是協方差為Ul的復高斯向量. 由于hml的BEM模型可寫作 hml=Bgml, (24) 式中:hml=(hm(0,l),hm(1,l),…,hm(N-1,l))T; gml=(g0(l),g1(l),…,gQ(l))T; B=(b0,b1,…,bQ)為BEM基函數矩陣. 所以,經過BEM模型轉換后的基系數可建立相似的AR模型,如式(25). gml=Aglg(m-1)l+uml, (25) 式中:Agl為BEM基系數的狀態轉移矩陣. AR模型參數可通過尤爾-沃克(Yule-Walker)方程解得 (26) 因為BEM系數是零均值的相關復高斯變量,其相關矩陣為 (27) 式中:s為相關移位的大小. 又由于本文采用的是Jakes模型信道[15],則 (28) fmax為最大多普勒頻移; Ts采樣周期; Ns=N+NCP為添加了CP的OFDM符號采樣點數,NCP為循環前綴的長度; J0(·)為第1類零階Bessel函數. 將各徑的AR模型結合表示為 gm=Aggm-1+um, (29) Ag=diag{Ag0,Ag1,…,Ag(L-1}為L(Q+1)×L(Q+1)的狀態轉移矩陣; 在本文中,將式(29)看作KF算法的狀態方程,將第m個符號對應頻域接收信號看作KF測量方程,表示如式(30). (30) 采用KF算法估計多個OFDM符號對應的BEM系數[13],具體步驟如下所示: 步驟1初始化 g0=0L(Q+1)×1, P0=Rg(0), Rg(s)=diag{Rg0(s),Rg1(s),…,Rg(L-1)(s)}. 步驟2時間更新方程 gm|m-1=Aggm-1, 步驟3測量更新方程 gm=gm|m-1+Km(Ym-Smgm|m-1), Pm=Pm|m-1-KmSmPm|m-1. 上述步驟中:gm|m-1、gm、Pm和Pm|m-1分別為第m個符號的參數預測值、參數估計值、估計誤差協方差矩陣和預測估計誤差協方差矩陣; IN為N階單位方陣. 通過Matlab仿真結果對算法性能進行驗證.仿真參數參考文獻[17]設置,如表1所示,仿真中采用QPSK (quadrature phase shift keying)調制,梳狀導頻,瑞利多徑信道模型,GCE-BEM(Q=2).參考指標歸一化多普勒頻移表示為 (31) 式中:v為移動速度; c為光速; fc為載波頻率. 表1 仿真參數表Tab.1 Simulation parameters 圖1為信噪比(SNR)為20 dB時,隨著fnd逐漸增大(fnd=0.1,0.2,0.3分別對應于速度v=150,300,450 km/h),各方法的信道估計NMSE(normalized MSE).其中,KF曲線對應于未采用CS時延估計(即認為主徑連續集中在前5徑且只估計前5徑)[13]時的估計誤差,其他3條曲線分別對應于采用OMP與LS、LMMSE和KF 3種方法的結合. 圖2為fnd=0.2時,隨著信噪比SNR增加,各方法的信道估計NMSE. 圖1 SNR為20 dB,fnd增大時,各方法的NMSE對比Fig.1 NMSE vs. fnd for SNR is 20 dB 圖2 fnd=0.2,SNR增大時,各方法的NMSE對比Fig.2 NMSE vs. SNR for fnd=0.2 圖1和圖2中:OMP-KF (orthogonal matching pursuit-KF)曲線為本文算法;OMP-LS和OMP-LMMSE曲線分別為將OMP與LS和LMMSE相結合的算法,這兩種算法未考慮相鄰符號塊信道參數的變化關系;KF曲線為文獻[13]中算法. 從圖1中可以看出,fnd增大時各方法的估計誤差都有所增加.其中,OMP-KF算法與只使用KF相比,由于應用了OMP進行稀疏信道環境下的時延估計,故誤差遠低于直接使用KF[13]的算法;而同時進行了時延估計的情況下,OMP-LMMSE算法考慮了噪聲和信道的統計信息,因此誤差低于OMP-LS,而OMP-KF算法由于考慮了相鄰符號之間的平滑關系,其誤差更低于OMP-LMMSE. 從圖2中可以看出,與圖1趨勢相同,進行了時延估計的OMP-KF算法誤差低于直接使用KF[13]的算法;而同樣進行了時延估計時,在SNR較低時,OMP-KF算法的NMSE低于OMP-LS和OMP-LMMSE,SNR增加時,OMP-KF算法優勢也增大,在SNR達到20 dB以后,誤差變化趨于平緩. 針對快時變稀疏環境下OFDM系統的信道估計問題,本文基于快時變信道的BEM模型,采用壓縮感知算法進行稀疏環境的時延估計,再采用卡爾曼濾波對BEM系數進行估計,從而得到信道增益.由于該算法綜合考慮了快時變、稀疏信道以及連續符號間的信道參數的平滑特性,相對于只考慮慢時變或非稀疏信道的算法,一定程度上提升了信道估計性能,最后通過仿真實驗進行了驗證.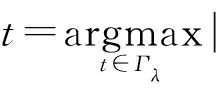
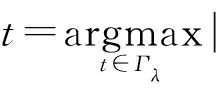
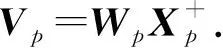
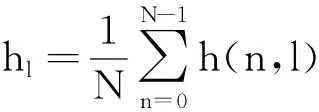
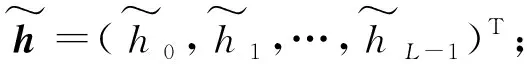
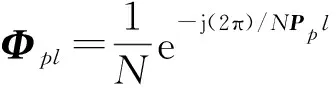
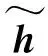
3 基于卡爾曼濾波的信道估計
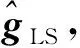
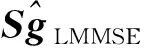
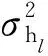
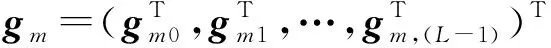
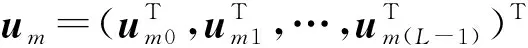

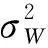
4 實驗仿真


5 結束語

