利用梯度結構張量檢測鹽丘與斷層

王清振 張金淼 姜秀娣 桑淑云

(中海油研究總院有限責任公司, 北京 100028)

1 引言

多年來，人們基于不同的理論提出了多種不連續性檢測方法。目前，斷層檢測技術是構造解釋中必備的一項技術。Bahorich等[1]提出了第一代相干體算法(C1)，這是基于二階統計量的算法，易于編程實現，簡單高效；Marfurt等[2]開發了利用任意數目的地震道估計相干性的算法(C2)，在利用相似性算法估計地層的連續性時，采用一系列試驗傾角截取地震道片段構造分析窗，在窗內計算地震波形的相干值，將與最大相干值對應的試驗傾角記為局部地層傾角； Gersztenkorn等[3]研發了一種基于特征結構的相干估計算法(C3)，由于特征結構分析可以給出更高的橫向分辨率和不連續性度量對比度，因此特征結構相干算法可以改善陡傾地層的連續性度量效果，但是同時會降低平緩地層區域的斷層成像效果； Marfurt 等[4]給出一種級聯方法解決上述局部傾角估計帶來的問題，首先利用相似算法估計局部地層傾角，然后應用具有較大分析窗的中值或均值濾波器平滑得到的傾角數據，以獲取可靠的地層傾角估計結果[5,6]，在此基礎上采用特征結構相干算法沿地層傾角作相干分析，能得到具有較高橫向分辨率的不連續性度量； Israel等[7]提出一種估計局部結構熵的算法(LSE)，具有很高的計算效率，又能較好地抑制噪聲，在選擇不同大小的分析單元后，可檢測不同尺度的不連續性。此外，三維體曲率屬性也是不連續性檢測的一大熱點技術[8-10]，尤其在檢測河道及裂縫型油氣儲層中效果顯著[11,12]。但是由于曲率計算過程中要對地震數據求兩次微分運算，而微分運算對噪聲較為敏感[13-15]，嚴重影響了曲率屬性的實際應用效果。Wang等[16]提出一種高抗噪性三維體曲率分析技術，能夠適用于低信噪比資料，特別是在陡傾地層發育區檢測結果的假象更少，可真實地反映地下斷層及巖性邊界等地質信息。王清振等[17]提出了基于高維物理小波變換的不連續性檢測技術，能夠更好地檢測小斷層、小河道等地質體邊界信息，并且具有較強的抗噪性。

在鹽巖劇烈活動地區，在鹽的擠壓下地層發生嚴重變形，形成復雜的構造特征，導致斷層識別困難，常規的相干和曲率算法很難取得理想的效果。Randen等[18]提出利用圖像處理中的梯度結構張量法對三維地震數據的梯度向量場進行平滑濾波，提取有用的地震結構信息。Luo等[19]、問雪等[20]發展了基于梯度結構張量的梯度向量平滑方法，將梯度結構張量構造過程中的三維高斯低通濾波函數替換為由復地震道瞬時能量作為加權值的數據自適應低通濾波方法，可大大提高傾角和方位角估計結果的空間一致性。Wang等[21]給出一種向量翻轉迭代濾波法平滑梯度向量場，該方法首先選定參考方向，將所有梯度向量針對參考方向進行翻轉，然后對得到的向量場進行均值平滑并且更新參考方向，通過迭代上述步驟取得最終的地層走向估計。這種方法避免了梯度結構張量方法在主特征值不存在時無法準確估計地層走向的問題。

基于前人對梯度結構張量性質的研究，本文提出了一種新的鹽丘和斷層檢測技術——梯度結構張量(GST)不連續性檢測技術。首先利用地震數據構造梯度結構張量，然后對梯度結構張量做特征分解，求取其特征值和特征向量，最后利用三個特征值的組合構建出一種混沌度量，從而有效識別復雜構造中的斷層及鹽丘發育范圍。實際數據應用表明，在鹽巖劇烈活動地區的斷層識別中，與C3、曲率等算法相比，GST方法能夠更好地克服由陡傾地層引起的不連續性假象，可清晰地反映真實的斷層信息和鹽丘發育范圍，為鹽丘的三維雕刻提供可靠的基礎數據。

2 技術原理

GST是分析和描述地震數據中構造特征的一種有效工具。該方法利用梯度矢量描述地質體的傾角和方位，采用梯度張量矩陣的譜分解描述地震數據的構造特征，可有效度量斷裂、河道、礁體內部紋理、平行與亞平行結構、傾斜層理、波狀層理等地質現象。梯度結構張量Mρ的定義為

(1)

采用標準差為ρ的各向同性高斯核Gρ對梯度向量的各個分量作光滑平均。其中Gρ是三維的標準高斯函數，其形式為

(2)

式中:U為原始地震數據；Uσ為平滑后的地震數據，其中σ為尺度參數，其取值取決于待分析數據的噪聲強度，即定義為噪聲尺度，可降低梯度數值計算對噪聲的敏感度，也建立了梯度結構張量可度量的最小構造尺度；Gσ為尺度參數為σ的各向同性高斯核。標準差ρ的選擇取決于構造度量和分析的分辨率，即定義為構造尺度，在ρ的高斯鄰域內平滑梯度張量，使其成為一個對稱半正定矩陣，提高了結構分析的魯棒性。

對梯度結構張量Mρ進行矩陣特征分解

(3)

式中：λ1≥λ2≥λ3≥0為Mρ的三個非負特征值；v1,v2,v3為對應的特征向量，它們構成一個局部的正交坐標系，v1表征局部鄰域內對比度最大的方向(信號的梯度方向)，v2和v3構成一個垂直于v1的局部平面。Mρ的三個特征值的含義與對應數據體中的空間結構特征關系如表1所示。

據此構建構造混沌度量如下

(4)

基于GST的混沌度量可有效反映局部構造的規則性，且不依賴于振幅變化。即：mchaos→1， 對應于橫向不連續性構造；mchaos→0， 對應于反射雜亂不規則區域；mchaos→-1， 對應于規則的層狀構造。

為了形象地說明混沌度量與空間結構特征的對應關系，引入一個半球形的鹽丘模型，用一組正弦波信號模擬地層反射。鹽丘內部為具有雜亂反射特征的不規則區域，鹽丘邊界為類似于斷層、巖性邊界等地質特征的線性結構，正弦波信號代表規則的層狀構造結構。由模擬結果(圖1)可見：鹽丘內部雜亂反射特征的GST檢測結果為0(圖中顯示為白色)；規則的層狀構造的GST檢測結果為-1(圖中顯示為紅色)；巖性邊界檢測結果則為1(圖中顯示為黑色)。模型數據說明GST算法可有效地識別三種空間結構類型。

表1 Mρ的三個特征值與空間結構特征對應關系

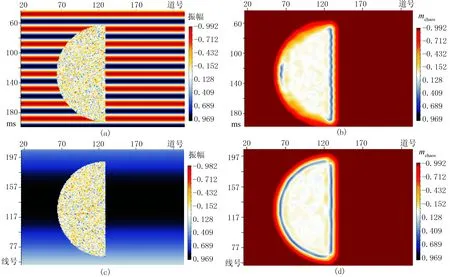
圖1 半球形鹽丘模型模擬結果

σ、ρ顯著影響檢測結果的分辨率。圖2為不同的σ、ρ取值的半球形鹽丘模型GST檢測結果時間切片。由圖可見：當ρ=4、σ分別取0.5(圖2a)、1.0(圖2c)和2.0(圖2e)時，隨著σ增大，檢測結果分辨率顯著降低； 當σ=0.5、ρ分別取2(圖2b)、3(圖2d)和5(圖2f)時，隨著ρ增大，檢測結果分辨率降低。在實際工作中σ的取值要考慮地震數據信噪比，即：當信噪比較高時σ要取較小值，可提高檢測精度；當信噪比較低時σ要取較大值，以降低噪聲的影響，可提高結果的穩定性。對ρ的選取則需要考慮具體的工作目標，即： 當檢測大尺度的不連續性信息時，則ρ取較大值；反之當檢測小尺度的不連續性信息時，則ρ取較小值。

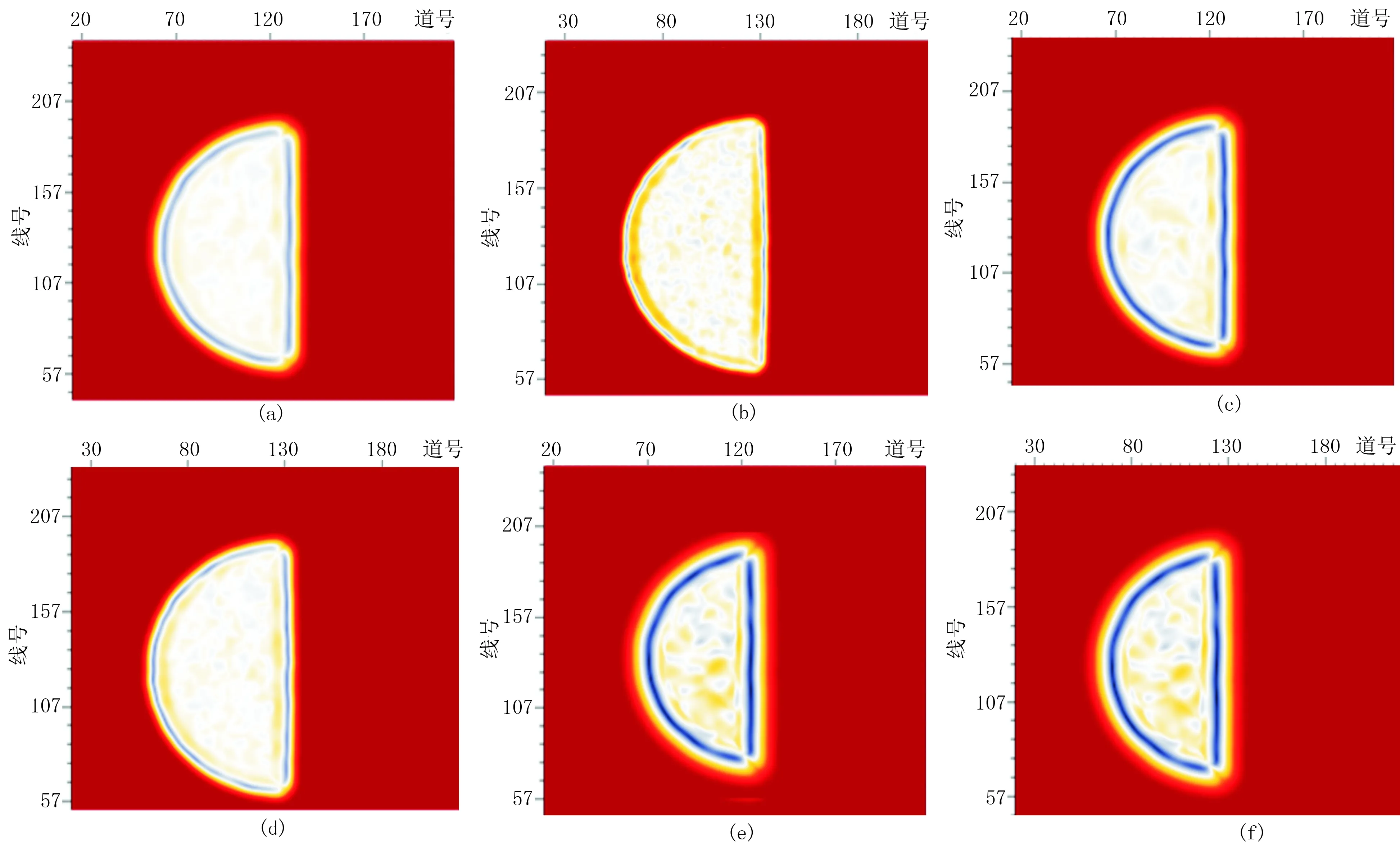
圖2 不同σ、ρ取值的半球形鹽丘模型GST檢測結果時間切片(128ms)

3 實際應用

利用GST在鹽巖發育區進行了測試。圖3為A區5835縱測線地震剖面及其C3、GST、最大正曲率檢測結果，圖4為A區地震數據4000ms時間切片及其C3、GST、最大正曲率檢測結果。由圖可見：①該區鹽巖極為發育且活動劇烈，鹽上地層由于受到鹽巖活動影響，發生劇烈的扭曲畸變，褶皺廣泛發育，地層傾角變化范圍為0°～90°，地層的復雜變化導致斷層識別困難，僅從剖面上很難直觀地解釋斷層(圖3a)；在地震數據時間切片中存在很多閉合圈，也形象地展示了鹽巖滑動對地層的劇烈改造作用(圖4a)。②由于地層傾角變化劇烈，C3算法無法有效地識別斷層，剖面檢測結果幾乎全是黑色高值區域(圖3b)，平面檢測結果也不能刻畫斷層分布和鹽丘展布(圖4b)。③曲率算法的效果略好，但剖面(圖3d)和平面檢測結果(圖4d)均不能準確地刻畫斷層聚焦度和鹽丘邊界，且在平面上由于整體高曲率值范圍太大，導致關鍵邊界信息不明顯，斷層不易識別。④在GST平面檢測結果中(圖4c)斷層清晰可見(紅藍箭頭指向)，在GST剖面檢測結果中也見斷層形跡(圖3c)，且GST平面檢測結果的黑色雜亂反射區域分布范圍(綠色框內)和剖面檢測結果的鹽巖發育區對應很好，說明GST能有效檢測鹽巖空間展布范圍。但是也可以看到，GST檢測結果的分辨率不高，尤其對傾斜斷層，斷點檢測結果與實際結果有一定的偏移量，這是因為在計算地層GST時使用各向同性高斯函數進行平滑，導致分辨率有所下降。

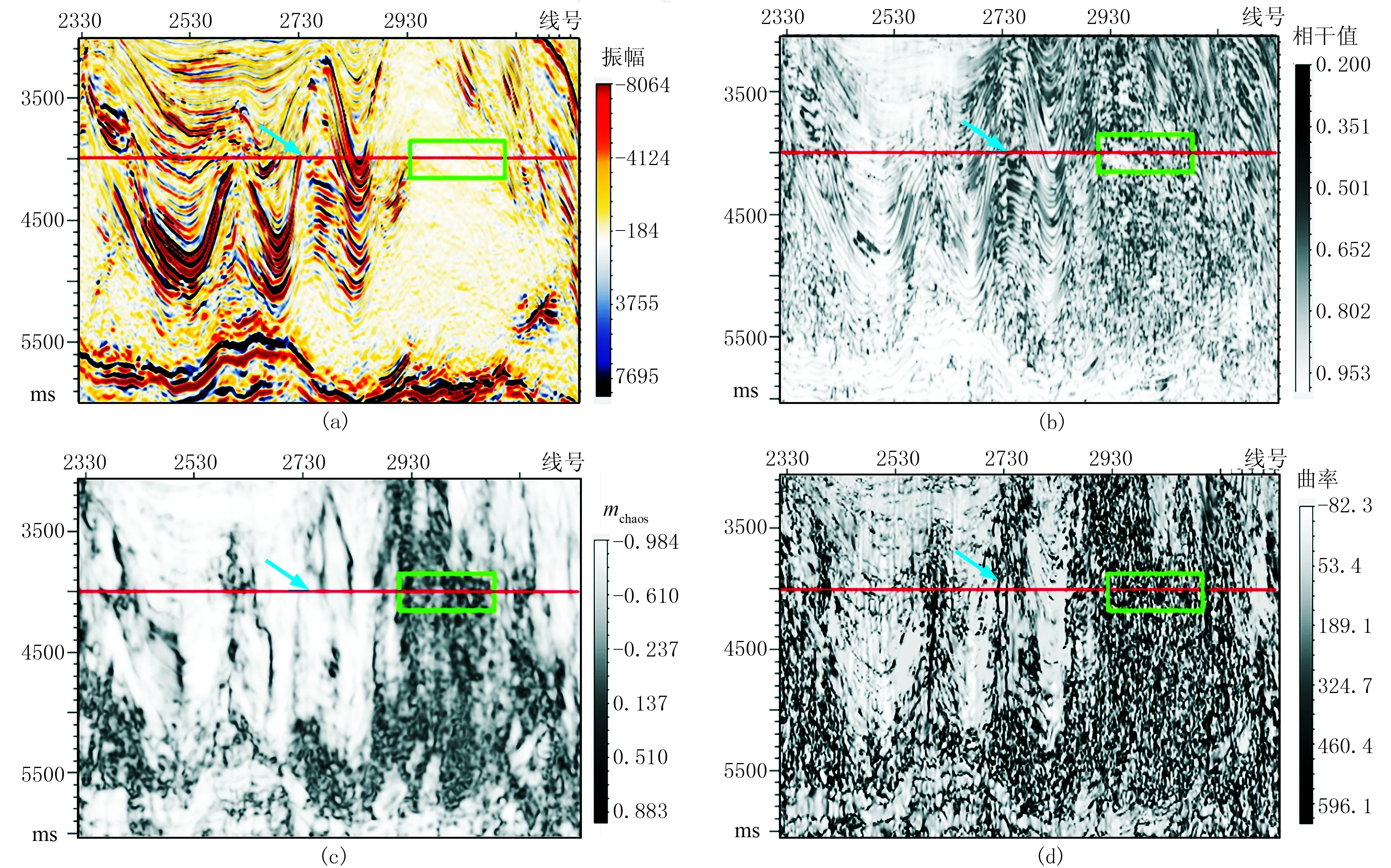
圖3 A區5835縱測線地震剖面(a)及其C3(b)、GST(σ=1，ρ=3)(c)、最大正曲率(d)檢測結果

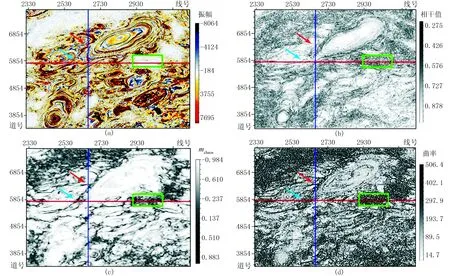
圖4 A區地震數據4000ms時間切片(a)及其C3(b)、GST(σ=1，ρ=3)(c)、最大正曲率(d)檢測結果

4 結論

在鹽巖發育區域，由于鹽巖具有易變形、易流動的特性，常常導致地層發生褶皺彎曲，形成極為復雜的構造特征，利用常規方法進行斷層和鹽邊界識別極為困難。由于地層傾角分布范圍很廣，根據傾角難以區分層位和斷層，常常導致異常檢測結果。為此，本文提出了一種基于地震資料梯度結構張量的鹽丘和斷層檢測技術，利用梯度結構張量可很好地反映不同構造特征，將三個特征向量進行有機組合構建一種混沌度量，可屏蔽彎曲地層的影響，有效識別斷層和鹽丘展布范圍。實際資料應用結果證實，該方法較第三代相干、曲率等常規方法更能適應鹽巖劇烈活動區的鹽丘與斷層識別，檢測的斷層更聚焦，鹽丘邊界更準確。尚須指出，由于計算地層梯度結構張量利用各向同性高斯函數進行平滑，因此檢測結果的分辨率不高，尤其對傾斜斷層，斷點檢測結果與實際結果有一定的偏移量。今后可以考慮根據局部構造特征構建基于各向異性介質的梯度結構張量，對初始梯度矩陣場做平均，以提高檢測結果的分辨率。