三維自由彎曲技術及變形區長度優化數值模擬研究

熊昊，萬柏方，陶杰，王林濤，程旋，魏文斌，郭訓忠

（1. 南京航空航天大學 材料科學與技術學院，南京 210016；2. 江蘇省核能裝備材料工程實驗室，南京 210016；3.江蘇圖南合金股份有限公司，江蘇 丹陽 212352）

隨著金屬彎曲成形技術的發展，空心構件已廣泛應 用于航天航空、汽車輪船、核能發電等領域，越來越多點焊或沖壓的鈑金零件被剛度更高的空心構件所取代以減輕重量[1]。作為各類液壓系統、氣壓系統、燃油系統等的管路、管道及其連接零部件，空心構件直接關系到裝備的運行安全[2—5]。這些空心構件通常采取彎曲成形工藝或者再附加液壓成形工藝。然而常規彎曲成形技術在復雜空心構件的快速精確成形方面存在瓶頸技術難題。如數控繞彎、型模推彎、拉彎、滾彎[6—8]等彎曲工藝無法成形連續變曲率及無直段連續彎曲的構件，并且如何要在成形過程中改變彎曲半徑，一般都需要進行卸載并更換系列彎曲模具夾具[9]。三維自由彎曲作為一項新興的彎曲技術，擁有了極大的彎曲潛力及復雜彎曲設計的可能性，特別適用于變彎曲半徑、無直段連續彎曲的液壓成形工藝的預彎曲構件。

三維自由彎曲成形技術源于日本科學家提出的MOS Bending技術[10]，通過控制彎曲模的運動軌跡（包括平動和轉動）并結合管材的軸向推進，可一次成形多種彎曲半徑條件和復雜軸線的空心構件。其中，彎曲半徑取決于彎曲模的位移量，彎曲角由坯料軸向送進的長度決定，彎曲軸線的變化和彎曲模在與管材軸向垂直平面內的相對位置有關。為了保證自由彎曲成形過程的準確性及產品的質量和精度，必須建立接近實際的仿真模型。下游成形工藝如液壓成形階段需要彎曲仿真結果，從而進行整體生產的可行性預測過程，以保持較低的模具成本。如果自由彎曲是終了成形工序，那么成形管件后續作為結構件必須對其碰撞性能和振動性能等進行有限元動態分析，這同樣需要自由仿真結果作為數據基礎。近年來隨著相關技術研究的發展，不同類型的自由彎曲構型及運動學理論被不斷完善[11—15]，同時商用的自由彎曲成形系統也被日本、德國等多家企業相繼推出[16—18]。其中日本Nissin公司推出的自由彎曲裝備可以滿足總長小于4000 mm、外徑為8～60.5 mm的管材任意彎曲角、任意彎曲軸線、相對彎曲半徑低至2.5 mm的空心構件的三維造型，且管材最大送料速度可達350 mm/s[19]。

文中將詳細介紹三維自由彎曲成形技術的基本原理及三維自由彎曲裝備的控制方式，并通過對制冷系統管路中的6061鋁合金復雜空心構件進行了三維自由彎曲成形過程數值模擬，分析了成形過程中彎曲段的應力應變狀態，同時研究了變形區長度A值這一關鍵成形工藝參數對彎曲成形結果的影響規律。基于模擬分析所得最優變形區長度，最后在三維自由彎曲裝備上對目標構件進行了彎曲成形試驗，并得到了成形質量較好和成形精度較高的管件。

1 三維自由彎曲成形技術

三維自由彎曲成形技術使管材、型材及線材任意的彎曲設計變得簡單，特別適用于復雜彎曲構件的批量生產。由于自由設計及彎曲外側壁厚減薄極小的技術優勢，三維自由彎曲成形技術特別適合作為汽車空心構件液壓成形的上游預彎曲工序。同時，自由彎曲成形構件具有均勻的壁厚分布及極小的截面畸變。基于以上兩點，自由彎曲成形構件無論是作為最終的承力結構件還是預彎曲零件，都具有明顯的技術特點及優良的使用性能。

1.1 三維自由彎曲成形基本原理

自由彎曲過程為管材在推塊的軸向作用力PL下，沿z方向推進，依次通過導向機構和彎曲模。管材送進的同時球面軸承在垂直于管材軸線方向的力Pu的作用下，帶動彎曲模在xy平面內運動，在Pu及PL的共同作用下管材發生彎曲。彎曲模球心到導向機構前端之間的水平距離稱為彎曲變形區長度A。在成形過程中，彎曲模離開初始與導向機構軸線同軸的位置，開始在xy平面內進行偏心運動，偏離到與導向機構軸線不同軸的某一位置后進行停留，此時彎曲模球心與導向機構軸線的相對距離稱為彎曲模偏心距U。一般來說，在成形過程中A值不發生變化，而彎曲模偏心距U的大小則與目標彎曲半徑有關。在成形過程中，管材的加載彎矩M與A值、U值存在的關系見式(1)[20]。

三維自由彎曲裝置及原理見圖1。彎曲模與球面軸承及導向機構相連接，這些球面連接使彎曲模在平動的同時發生相應的轉動。球面軸承在x和y方向的位移由交流伺服電機控制。推塊的運動靠傳動鏈條帶動。在彎曲過程中，管材潤滑塊自動加油潤滑，同時尾部的推塊能防止其管材繞自身軸線轉動。由于管材被推塊施加了軸向的推力，使管材的應力狀態得到改善，從而減小了管材彎曲段外弧側的應變量和壁厚減薄率。值得一提的是，極小的外弧壁厚減薄率使自由彎曲成形技術在液壓成形工藝鏈領域具有廣泛的應用前景。

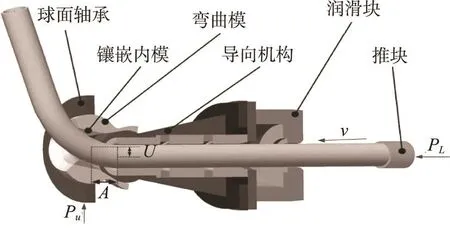
圖1 三維自由彎曲裝置及原理Fig.1 Three-dimensional free-bending and device

1.2 三維自由彎曲裝備控制程序

在三軸自由彎曲成形系統中，伺服電機及傳動鏈條由CNC數控系統控制，并且xyz方向的運動均為勻速。三維自由彎曲成形系統見圖2，自由彎曲的數控程序通過輸入的彎曲參數計算得到，包括管材進給速度v、直線長度Ln、彎曲半徑Rn、彎曲角θn、彎曲方向角ψn（表征了各彎曲平面的相對位置）。輸入彎曲參數后，幾何軟件計算出每一彎段彎曲模的偏移量及管材的軸向進給長度，從而得到相應的彎曲程序。

根據圖2b所示的參數得到一個簡單的程序如下。

其中G01代表常規操作命令，x,y代表彎曲模在x-y平面的絕對坐標，z代表管材z向送進長度，F代表管材z向送進速度，M02代表彎曲終止命令。此彎曲數控程序中彎曲模在x-y平面的坐標可通過式(2)和式(3)計算。

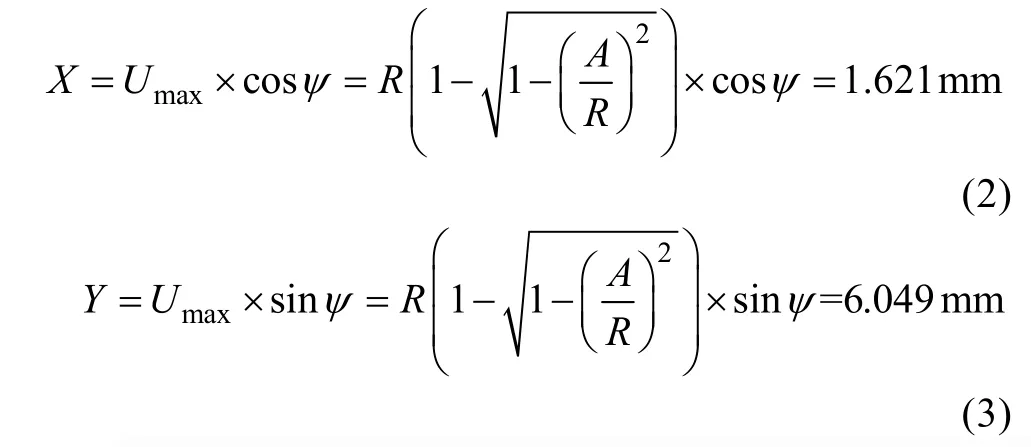
整個彎曲過程中，管材在z向的推進速度F設置為常量，并且速度與大小彎曲模在xy平面的運動速度有一定的匹配關系。彎曲模運動速度與管材送進速度的關系見圖3，彎曲模在x-y平面內的運動速度可通過式(4)—(7)計算。

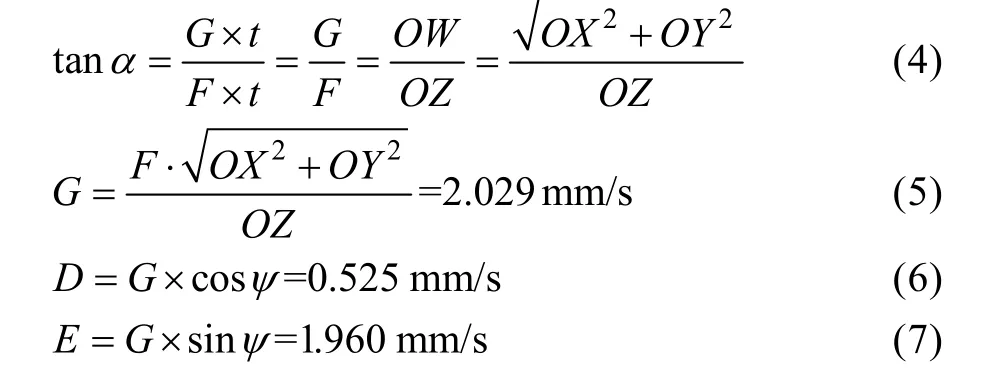
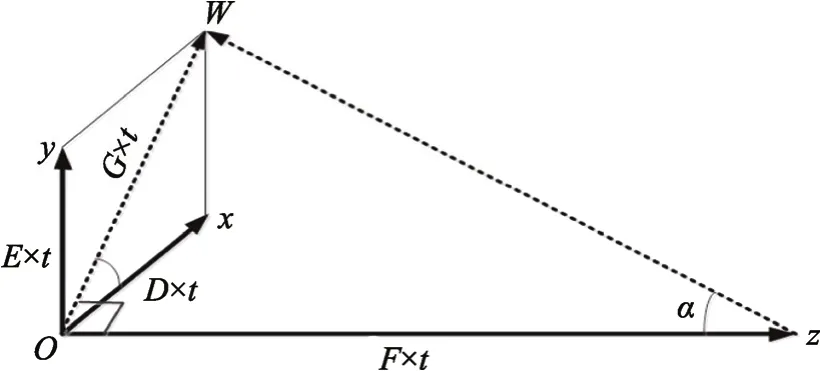
圖3 彎曲模運動速度與管材送進速度的關系Fig.3 Relationship between movement speed of bending die and feed speed of tube

2 復雜空心構件三維自由彎曲工藝分析

擬對制冷系統管路中的6061鋁合金管件的三維自由彎曲工藝過程進行有限元模擬。目標管件的三維模型見圖4，其中P1—P4為4個彎曲平面。目標管件的外徑為 15 mm，壁厚為 2 mm，軸向總長為 1558 mm，各個彎曲平面的具體尺寸見表1，其中ψn表示各個彎曲平面的夾角（銳角）。

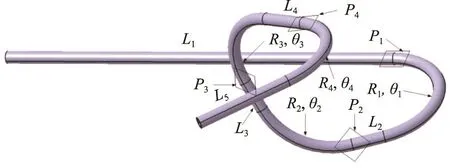
圖4 目標管件的三維模型Fig.4 Three-dimensional model of target tubular component

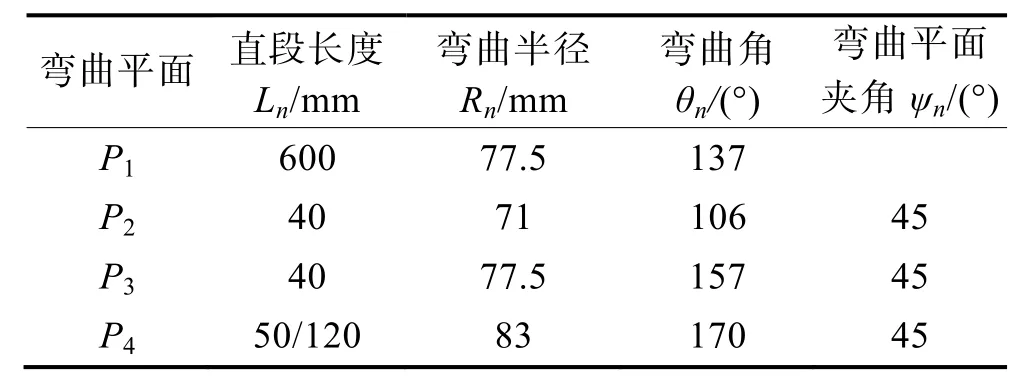
表1 目標管件的具體尺寸Tab.1 Specific dimensions of target tubular component

在不更換模具的情況下，傳統的彎曲工藝無法一次性成形這種復雜的變半徑的空間立體彎管，如果采用多次成形加工則容易產生截面畸變和累計誤差，并且管件的表面質量也不能保證，若采用三維自由彎曲成形技術則能輕松解決上述問題。自由彎曲工藝解析示意圖見圖5，在三維自由彎曲成形過程中，成形一個彎段通常需經過3個階段，包括兩個過渡段（彎曲模進程和回程）和一個圓弧段（彎曲模靜止）[21]。目標管件分段成形示意圖見圖6，在制定具體成形過程的參數時，需對此管件的彎曲段進一步分為圓弧段和過渡段，加上已有的直線段，此管件可分為16段成形過程。

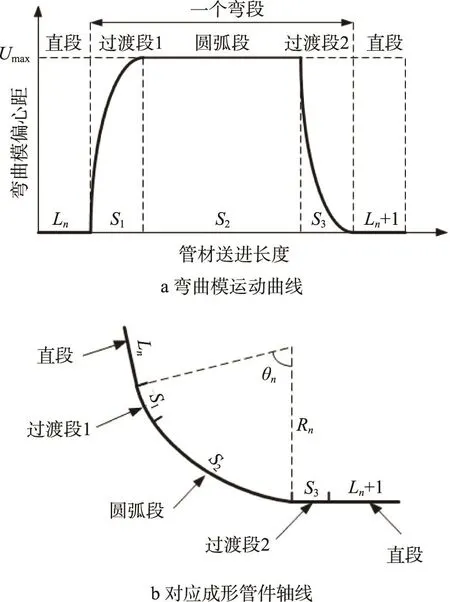
圖5 自由彎曲工藝解析示意圖Fig.5 Schematic diagram of free bending process

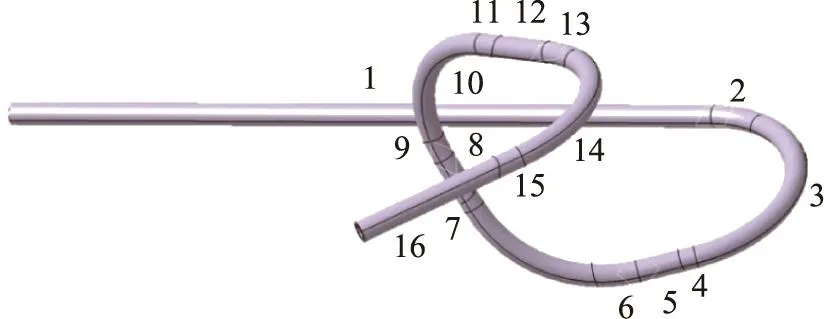
圖6 目標管件分段成形示意圖Fig.6 Schematic diagram of segment forming of target tubular component

3 三維自由彎曲有限元模擬研究

3.1 有限元模型

三維自由彎曲的有限元模型見圖7。該模型包含球面軸承、彎曲模、導向機構、壓緊機構、推進機構、管材6個部分。管材和彎曲模（被動運動，不設置為剛體）設置為可變形實體，網格劃分為C3D8R類型，其他部件均設置為剛體，網格類型為C3D10M。管材材料的本構關系為δ=Kεn，材料參數設置見表2。分析步設置為動力顯式。相互作用設為通用接觸，管材與模具切向全局摩擦因數設置為0.02。載荷設置中壓緊機構和導向機構設置其為完全固定，推進機構沿z向設置指定運動速度，并約束其余全部自由度，球面軸承設置沿x和y方向的運動速度，其余自由度全部固定，管材不設置載荷。

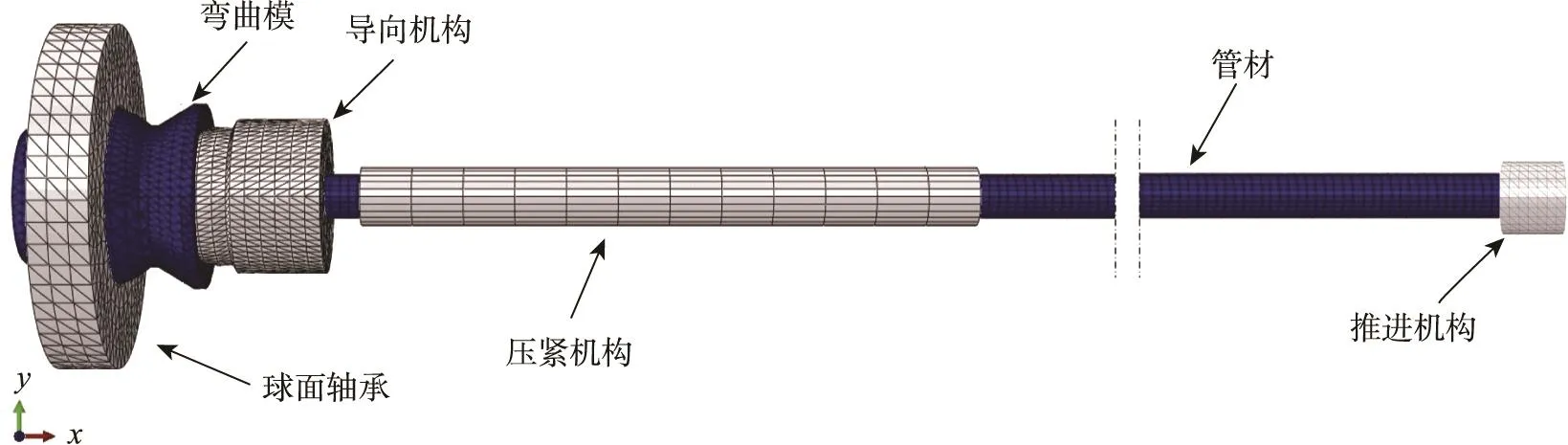
圖7 三維自由彎曲有限元模型Fig.7 Three-dimensional free-bending finite element model

表2 管材材料參數設置Tab.2 Parameters Setting of Tube Material

3.2 三維自由彎曲過程受力分析

在三維自由彎曲成形過程中，管材在軸向推力及彎曲模垂直管材軸向作用力的共同作用下，產生彎矩M進而彎曲成形。彎曲成形時，管材不斷推入固定的導向機構及偏離平衡位置的彎曲模之間，因此管材的彎曲變形區是在彎曲模中心與導向機構前端之間的部分，也就是A值長度的范圍。三維自由彎曲一般受力過程見圖8。在管材彎曲成形的開始即過渡段 1，彎曲模從平衡位置出發（U=0）向預定偏心距位置（U=UR，大小與彎曲半徑有關，方向與彎曲平面相對位置有關）運動，此過程中彎曲模偏心與管材軸向送進同時進行，彎曲變形區的應力集中在靠近導向機構前端的部分且內外側都有分布，而彎曲附近的管材應力值不大。管材彎曲成形的第二階段是為成形管件的圓弧段部分，在此階段彎曲模在預定偏心距保持靜止，但管材的軸向送進依然進行（送進長度與彎曲角有關），彎曲模對管材外側施加位置垂直管材軸向的壓應力，因此在彎曲模中心的管材外側也出現高應力狀態。事實上，不同于數控繞彎中管材內側受彎曲模作用，管材在自由彎曲過程中都是外側受彎曲模作用。圓弧段結束后，已成形部分已具有所需要的彎曲半徑和彎曲角。在彎曲的最后一部分即過渡段2，彎曲模和導向機構都不對管材產生作用，但管材外側仍然受切向拉應力，部分出現應力集中。

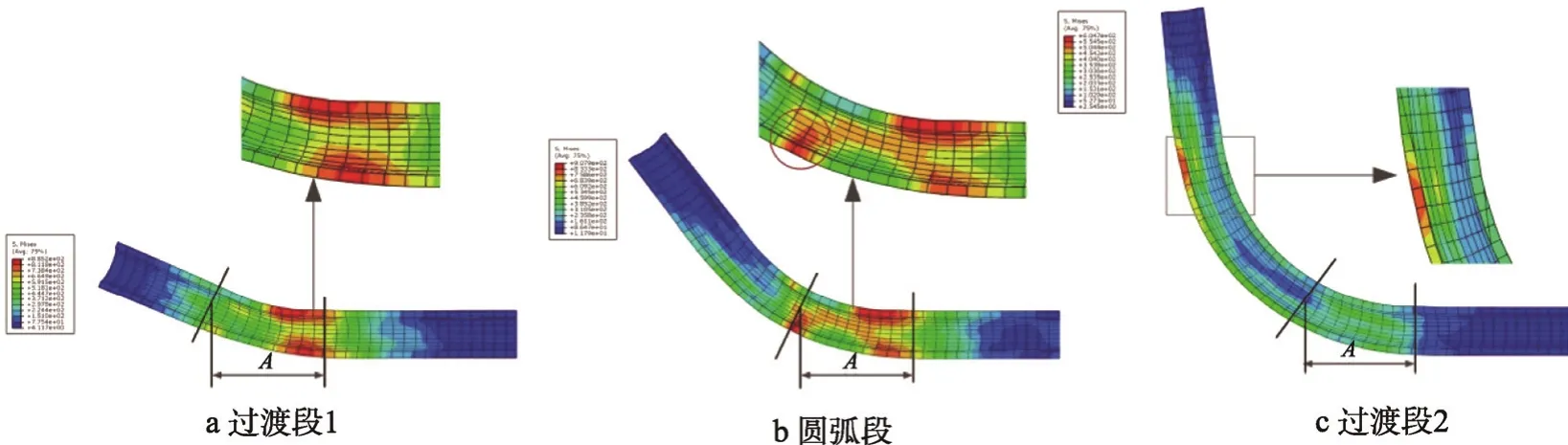
圖8 管材三維自由彎曲受力過程Fig.8 Stress process for three-dimensional free-bending of tube

3.3 彎曲變形區長度A對成形結果的影響

基于理論計算式(1)和(2)，管材彎曲半徑一定的條件下，管材的加載彎矩M、彎曲模的偏心距U及其速度時間曲線與彎曲變形區長度A有關，A的大小對管件的成形質量和成形精度具有很大的影響。若A值過小，則管材變形區軸向長度過短，在彎曲過程中管材靠近導向機構和彎曲模處的內側和外側受壓嚴重，使管材內側壁厚劇烈增大，出現截面嚴重扁化甚至失穩的現象，若A值過大則管材變形區軸向長度過長，管材的外側減薄率會增大，并且A值的增大也會導致相應彎曲半徑的彎曲模偏心距過大，甚至可能超過其最大工作行程，從而使管材產生嚴重的成形缺陷，因此無論是在進行有限元模擬還是實際成形試驗時，尋找合適的A值大小對提高彎管的成形質量和成形精度具有重要意義。

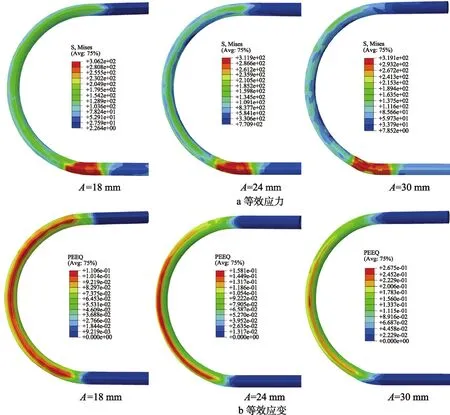
圖9 不同A值下的U形管模擬結果Fig.9 Simulation results of U tubular component under different A values

不同A值下的U形管三維自由彎曲成形模擬結果的等效應力云圖及等效應變云圖見圖9。從等效應力看，自由彎曲過程中的峰值應力隨著A值的增大而增大，這是由于在軸向推力PL、垂直軸向作用力Pu一定的條件下，A值越大，彎曲模偏心距U越大，裝備加載彎矩M越大。從等效應變看，自由彎曲過程中的管材外側峰值應變隨A值的增大而增大，說明管材外側減薄趨勢隨著A值的增大而增大。不同A值下模擬成形管件的壁厚變化、截面畸變及彎曲模偏心距情況見圖10。可以看出，模擬成形管件的最大壁厚增厚率及最大截面畸變率隨A值的增大而增大，最大壁厚減薄率隨A值的增大而減小，最大壁厚增厚率折線與最大壁厚減薄率折線在A值為21～24 mm區域內相交，故取A=22.5 mm為最優工藝參數。

3.4 目標管件的模擬成形過程

基于上述最優彎曲變形區長度A值，對目標管件進行整體三維自由彎曲成形仿真模擬，目標管件有限元自由彎曲模擬成形過程見圖11。模擬結果整體形狀和設計模型完全一致，尺寸精度也十分接近，但為了達到實際生產應用的要求，必須在實際試驗中驗證模擬結果和繼續優化工藝參數。

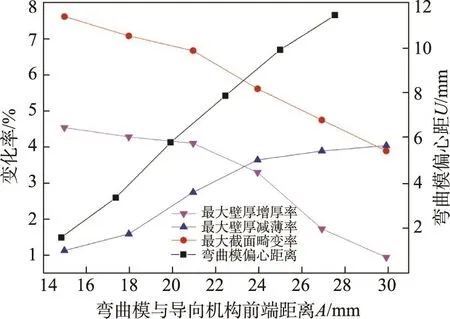
圖10 不同A值下模擬成形管件的成形質量Fig.10 Tube forming quality under different A values

圖11 目標管件有限元自由彎曲模擬成形過程Fig.11 Simulation of free bending process of target tubular component

4 自由彎曲成形試驗

圖12 三維自由彎曲成形試驗Fig.12 Test for three-dimensional free bending

基于上述模擬仿真得出的最優彎曲變形區長度A值，在自主研制的三維自由彎曲成形裝備上進行了實際的彎曲試驗，如圖12所示。試驗結果與三維數模和模擬結果的形狀對比見圖13，可以看出三者的形狀完全一致。表3為試驗成形管件的幾何尺寸、誤差對比及個彎曲平面內的最大壁厚減薄率、最大截面畸變率。可以看出管件的直段長度及彎曲角與設計尺寸相差較大，而彎曲半徑及彎曲平面夾角的誤差相對較小。直段長度及彎曲角涉及到過渡段問題，為了提高成形進度，必須根據實際裝備對理論計算公式進一步修正。管件最大壁厚減薄率不超過 9%，最大截面畸變率不超過5%，具有較好的成形質量。

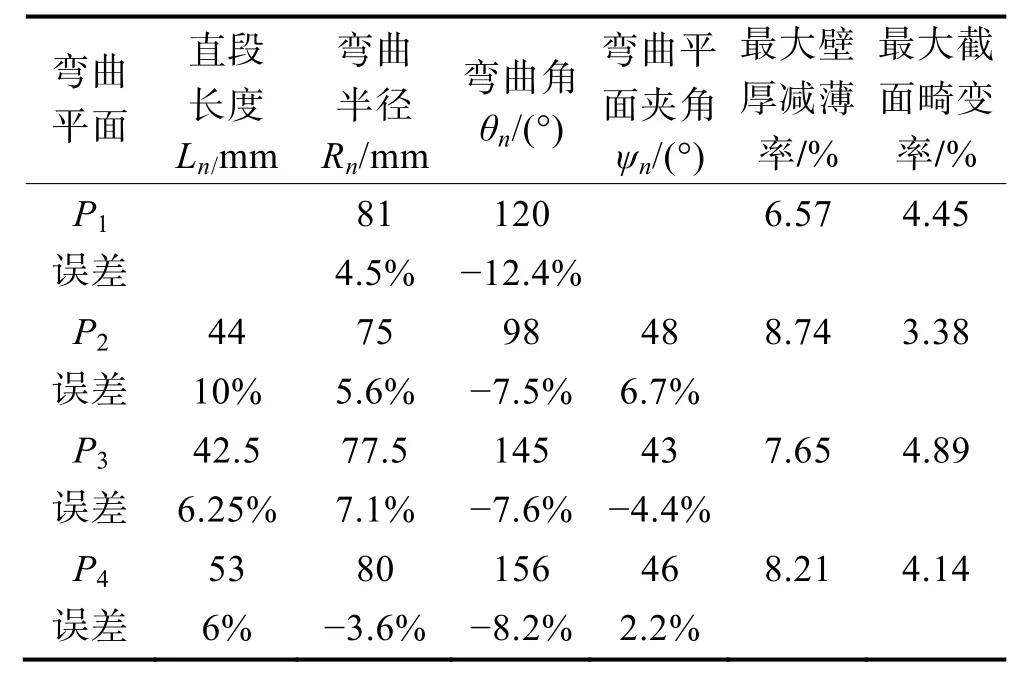
表3 成形管件的幾何尺寸、誤差及其成形質量Tab.3 Geometrical dimensions, errors, and forming quality of formed tubular component

5 結論

1) 三維自由成形技術僅通過控制彎曲模在平面內的平動及在空間內的轉動，無需進行彎曲模具的卸載即可實現管材彎曲半徑、彎曲平面的連續變化，一次精確成形復雜空間彎管構件。

2) 基于有限元模擬研究了彎曲模球心到導向機構前端之間的距離A對成形質量的影響規律。最大壁厚增厚率及最大截面畸變率隨A值的增大而增大，最大壁厚減薄率隨A值的增大而減小。

3) 基于有限模擬得出的最優彎曲變形區長度(A=22.5 mm)對目標管件進行了實際的彎曲成形試驗。試驗結果表明，成形管件的直段長度及彎曲角與設計尺寸相差較大，而彎曲半徑及彎曲平面夾角的誤差相對較小，管件最大壁厚減薄率不超過 9%，最大截面畸變率不超過5%，具有較好的成形質量。