大型數(shù)據(jù)表格取整算法研究

劉杰

1 引言

通信工程的設(shè)計由說明、圖紙和預(yù)算共三部分組成，其中預(yù)算要求每個站點(diǎn)做一個，預(yù)算金額保留兩位小數(shù)，并提供預(yù)算匯總表。預(yù)算匯總表樣式如表1所示，其中灰色填充部分為小計項(xiàng)和合計項(xiàng)（下稱“和項(xiàng)”），無顏色填充部分為單項(xiàng)材料金額（下稱“細(xì)項(xiàng)”）。

表1 預(yù)算匯總表樣式

在某些情況下，預(yù)算匯總表的金額是不能帶小數(shù)點(diǎn)的（例如工程預(yù)算的批復(fù)），因此需要對預(yù)算表格進(jìn)行取整。取整的要求為：所有數(shù)據(jù)必須為整數(shù)，數(shù)據(jù)取整前后差額的絕對值小于1，數(shù)據(jù)行列相加等式必須成立。

當(dāng)材料的類別大于10（M>10）、材料項(xiàng)大于100、站點(diǎn)數(shù)量大于100（N>10）時，這將是一個非常龐大的數(shù)據(jù)表格。除了通信工程設(shè)計的預(yù)算匯總表外，其他領(lǐng)域也有類似的數(shù)據(jù)表格需要取整，因此本文研究的內(nèi)容為大型數(shù)據(jù)表格的取整算法，以上述表格為例作為研究對象。

2 四舍五入會增加算法復(fù)雜度

對小數(shù)取整有三種方式：四舍五入、向上取整和向下取整。但是在算法上如果采用四舍五入方式的話，將會增加算法的復(fù)雜度，如表2所示。

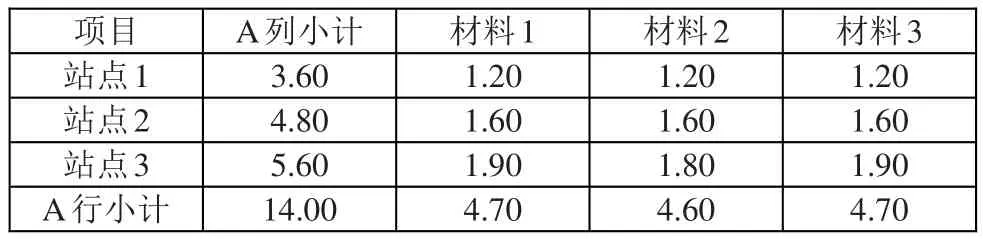
表2 四舍五入取整例子原數(shù)據(jù)

對表格中的數(shù)據(jù)四舍五入取整后，需要對部分?jǐn)?shù)據(jù)進(jìn)行加1操作，需要對部分?jǐn)?shù)據(jù)進(jìn)行減1操作，以使得最終的結(jié)果滿足取整的要求，如表3所示。

表3 四舍五入取整例子結(jié)果

在上述的例子中，數(shù)據(jù)四舍五入取整后，由于數(shù)據(jù)小數(shù)點(diǎn)后的數(shù)值有大有小，導(dǎo)致取整后數(shù)據(jù)的調(diào)整方向有兩個，某些數(shù)據(jù)需要向上加1，某些數(shù)據(jù)需要向下減1。數(shù)據(jù)調(diào)整方向越多，在算法實(shí)現(xiàn)上就會越復(fù)雜。如果對數(shù)據(jù)向上取整或向下取整，取整后數(shù)據(jù)的調(diào)整方向只有一個，向下減1或向上加1，程序?qū)崿F(xiàn)上較為簡單。

為了使算法更為簡潔，本文選擇向下取整的方式。筆者已經(jīng)在Excel通過VBA編程實(shí)現(xiàn)了取整算法，下面對此算法進(jìn)行詳細(xì)的闡述。

3 取整算法

面對龐大且層級較多的數(shù)據(jù)表格時，為了更方便處理數(shù)據(jù)，需要對表格進(jìn)行分析，取得其基本組成單元。通過分析，所有的數(shù)據(jù)表格均可分為兩個基本單元：一維數(shù)組和兩維數(shù)組，下面對這兩個基本單元的概念及取整算法說明。

3.1 一維數(shù)組表格取整算法

一維數(shù)組表格指的是在取整計算時，只需要考慮一個維度（行或列）的等式是否成立即可。具體步驟為：

（1）對數(shù)據(jù)進(jìn)行向下取整；

（2）判斷和項(xiàng)、細(xì)項(xiàng)相加得到的和之間的差額，差額表格需要對細(xì)項(xiàng)進(jìn)行調(diào)整的次數(shù)或項(xiàng)數(shù)；

（3）計算每一個細(xì)項(xiàng)取整前后的差額，把差額最大的細(xì)項(xiàng)加1。直到第2步計算得的差額為0，即完成了一維數(shù)組的取整。

3.2 兩維數(shù)組表格取整算法

兩維數(shù)組表格指的是在取整時，需要考慮兩個維度（行和列）的等式是否成立，下面以一個兩維數(shù)組進(jìn)行詳細(xì)說明，如表4所示。

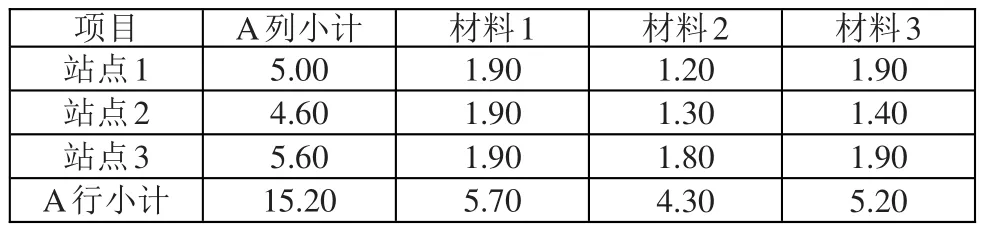
表4 兩維數(shù)組表格取整算法例子原數(shù)據(jù)

具體步驟為：

（1）對數(shù)據(jù)進(jìn)行向下取整；

（2）判斷行、列和項(xiàng)與取整后細(xì)項(xiàng)和的差額，求得列差額分別為5-（1+1+1）=2、4-（1+1+1）=1、5-（1+1+1）=2，求得行差額分別為5-（1+1+1）=2、4-（1+1+1）=1、5-（1+1+1）=2，列差額與行差額組成了一個表格的行合計和列合計。使用由上而下、由左而右的方式遍歷所有單元格，如其對應(yīng)的列差額、行差額均大于1，且細(xì)項(xiàng)原數(shù)據(jù)小數(shù)點(diǎn)后有數(shù)值，即對該單元格進(jìn)行加1操作，最終得到結(jié)果如表5。

表5 兩維數(shù)組表格行列差額分配表

（3）完成第2步后，很多時候會存在行列等式不成立的情況，需要對這個表格進(jìn)一步調(diào)整。使用由上而下、由左而右對每一列未加1操作的單元格進(jìn)行遍歷，判斷細(xì)項(xiàng)原數(shù)據(jù)小數(shù)點(diǎn)后是否有數(shù)值，如是即進(jìn)行加1操作。再判斷同一列在第二步已經(jīng)進(jìn)行加1操作的單元格，其所在行與不相等列相交的單元格是否已經(jīng)有加1操作，且細(xì)項(xiàng)原數(shù)據(jù)小數(shù)點(diǎn)后有數(shù)值的話，加1操作進(jìn)行互換，如表6所示。

表6 行列差額二次分配表

（4）根據(jù)第3步得到的加1操作表格，在數(shù)據(jù)表格相應(yīng)位置對向下取整的細(xì)項(xiàng)進(jìn)行加1即完成了兩維數(shù)組的取整計算。

4 表格分層

對于計算機(jī)程序來說，需要將龐大的數(shù)據(jù)表格進(jìn)行拆分簡化，以方便程序處理。依據(jù)該表格的特性，本算法把表格拆分為四個層次的表格。

（1）第一層：提取數(shù)據(jù)表格的M列小計、列合計與N行小計、行合計相交的單元格，由這些單元格組成第一層表格，如表7所示。

表7 第一層數(shù)據(jù)表格

首先需要對工程合計數(shù)值進(jìn)行四舍五入，確定數(shù)據(jù)表格的總和，見上表標(biāo)圓形的單元格。然后對行合計、列合計進(jìn)行取整，利用一維數(shù)組取整算法處理即可完成。完成此部分后，M列小計與N行小計組成了一個兩維數(shù)組，利用兩維數(shù)組取整算法，即可完成第一層數(shù)據(jù)表格的取整。

（2）第二層：提取數(shù)據(jù)表格的M列小計、列合計與站點(diǎn)行、行小計相交的單元格，由這些單元格組成第二層表格。第二層共有N個表格，大致表格如表8所示。

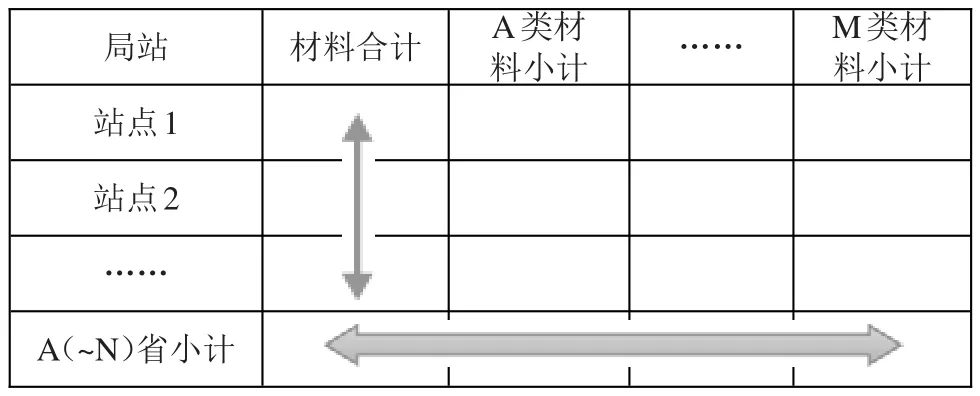
表8 第二層數(shù)據(jù)表格

通過第一層的調(diào)整計算，A（～N）省小計的值已經(jīng)確定，列合計與站點(diǎn)行相交的單元格組成了一維數(shù)組，利用一維數(shù)組取整算法處理。完成此步后，M列小計與站點(diǎn)行相交的單元格就組成了一個兩維數(shù)組，接著利用兩維數(shù)組取整算法處理。按此步驟把第二層N個表格處理完成后，即完成了第二層的取整。

（3）第三層：提取數(shù)據(jù)表格的列小計、材料列與行小計、行合計相交的單元格，由這些單元格組成第三層表格。第二層共有M個表格，大致表格如表9所示。

表9 第三層數(shù)據(jù)表格

通過第一層的取整計算，列小計與行合計相交單元格的值已經(jīng)確定，通過第二層的取整計算，列小計與行小計相交單元格的值也已經(jīng)確定。材料列與行小計相交的單元格組成了一維數(shù)組，利用一維數(shù)組取整算法處理。完成此步后，材料列與行小計相交的單元格就組成了一個兩維數(shù)組，接著利用兩維數(shù)組取整算法處理。按此步驟把第三層M個表格處理完成后，即完成了第三層的取整計算。

（4）第四層：提取數(shù)據(jù)表格的列小計、材料列與行小計、站點(diǎn)行相交的單元格，由這些單元格組成第四層表格。第四層共有M×N個表格，大致表格如表10所示。

表10 第四層數(shù)據(jù)表格

通過第二層的取整，列小計與站點(diǎn)行相交單元格的值已經(jīng)確定，通過第三層的取整，材料列與行小計相交單元格的值也已經(jīng)確定。材料列與站點(diǎn)行相交的單元格組成了一個兩維數(shù)組，接著利用兩維數(shù)組取整算法處理。按此步驟把第四層M×N個表格處理完成后，即完成了第四層的取整計算。

完成以上四個層次表格的取整后，整個大型數(shù)據(jù)表格的取整工作完成。

5 結(jié)束語

本文取整算法的實(shí)現(xiàn)，使得大型數(shù)據(jù)表格的取整工作變得非常簡單、快捷，極大地提高了工作效率和節(jié)省了人力成本，在實(shí)際應(yīng)用上具有很大的意義。