大約束長度卷積碼編碼器的改進與實現*

張濤濤，王滿喜，榮 輝，楊志飛

（1.電子信息系統復雜電磁環境效應國家重點實驗室，河南 洛陽 471003；2.中國洛陽電子裝備試驗中心，河南 洛陽 471003）

0 引 言

對于卷積碼而言，并沒有可用的代數結構構造好的卷積碼編碼器。考慮到生成多項式為G(X)=1+X+X2+X4+X8+X10的（15，5）BCH 碼 的 最小距離dg=7，對偶碼的生成多項式是h(X)=(X15-1)/g(X)=X5+X3+X+1且dg=4。符合生成多項式g(D)=1+D+D2+D4+D5+D8+D10且碼率為R=1/2的卷積碼有dfree≥min(7,8)。生成矩陣為 G(D)=[1+D+D2+D4+D51+D2]。可以看出，該編碼器的最小自由距離為dfree=7，約束長度為5。類似的構造可以產生碼率為1/2的卷積碼，然而構造這類卷積碼有兩個困難。第一個難題是尋找具有最大自由距離的大約束長度的卷積碼，第二個難題是此限與循環碼的最小距離有關。該難題已由Juestesen解決[1]。Jusetesen的構造限dfree≥dg，但它涉及到關于g(X )根的條件相當復雜，且在二進制情況下，僅僅可用來構造奇數n值的卷積碼。Tanner的構造得到限dfree≥dmin，其中dmin是相聯系的循環碼的最小距離[2]。

一般構造大約束長度的卷積碼要考慮編碼器的性能。卷積碼編碼器的糾錯能力與自由距離之間存在緊密聯系。具體來講，編碼器的性能與卷積碼的自由距離之間存在正相關關系。也就是說，編碼器的性能會隨自由距離的增加而得到改善。因此，要改善編碼器的性能，就要從卷積碼的自由距離入手，通過分析對比大約束長度卷積碼編碼器的自由距離，達到尋找好的大約束長度卷積碼編碼器的目的。一旦卷積碼的碼率確定了，就可以把卷積碼的自由距離和距離譜作為尋找好的卷積碼編碼器的指導。維特比譯碼和序列譯碼的性能主要受卷積碼的列距離特性的影響[3]。對于序列譯碼，卷積碼的列距離dl應該隨著l增加，至少是非減少的[4-6]，由此得到具有良好距離特性的卷積碼。

1 已有的搜索算法

大多數情況下，搜索大約束長度卷積碼的工作量隨著卷積碼約束長度的增加而迅速增加。利用計算機搜索好的大約束長度的卷積碼是非常耗時的運算，因此計算機搜索只能被限定在較短的約束長度。但是，即便對于小的約束長度，窮搜索的方法也是不可行的[7-8]。因此，需要提出新的篩選規則尋找好的卷積碼。Bahl、Cullum、Frazer和Jelinek提出了一種的基于維特比算法尋找dfree和Adfree的計算機搜索方法[9]，并由Larsen修改[10]該算法，假設接收到的序列全是零，把在柵格中的搜索限制在以一個非零信息分組開始的路徑，采用0量度代表一致，+1代表不一致，搜索具有最小量度的路徑。一旦在零狀態的幸存路徑的量度低于或等于其他所有路徑，算法就可以停止。所以，在全零狀態下的量度就等于dfree，這是因為沒有一條其他幸存的路徑能以更小的量度匯合到全零狀態。對于惡性編碼器，由于狀態圖中的零環路，在全零狀態下的幸存路徑可能無法達到最小的量度。該算法能夠計算約束長度為20的卷積碼的dfree和最小自由距離為dfree的個數Adfree。對于更大的約束長度，算法要存儲的空間數隨著約束長度的增加呈指數倍數增加而無法滿足，因此必須嘗試其他方法來尋找dfree。

2 改進的搜索算法

對于較大的約束長度，目前還沒有通用的計算dfree的方法。傳統的利用計算機搜索大約束長度的卷積碼的算法在文獻[11-12]中已有介紹，能做到的最大約束長度不超過30。為了能夠找到約束長度在30以上的卷積碼，需找到一種新的方法尋找更大約束長度的卷積碼。

單次尋找大約束長度最優卷積碼的算法流程如圖1所示。

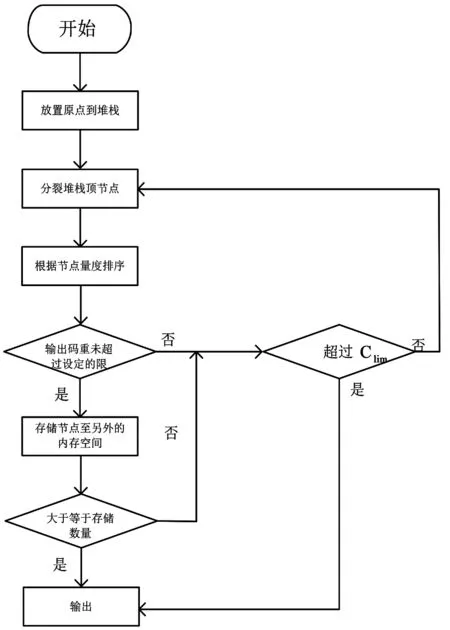
圖1 計算機搜索卷積碼的堆棧算法流程

通過對卷積碼自身特性和堆棧算法的研究，提出了快速尋找有限數量好的大約束長度的卷積碼方法。

（1）隨機設計首位和末位分別為1，生成多項式重量不同時為偶的編碼器。

（2）檢驗（1）中設計的編碼器的距離分布特性。

（3）驗證（1）中設計的編碼器的自由距離是否符合預估的上限和下限。

對于碼樹圖中的節點，需要設置一個結構體。該結構體中應該包含有分裂到該節點的狀態、該節點的碼重、當前節點的量度和當前的狀態到全零狀態所需的最少分裂次數。算法開始時，放置一個初始狀態為1，碼重為2，當前的狀態到全零狀態所需的最少分裂次數為編碼器的約束長度，節點的量度為碼重和當前狀態到全零狀態所需最少分裂次數的和。對棧頂的節點進行分裂，每次分裂都是分別進行0和1的分裂。如果分裂后的節點的碼重滿足設定的上限，則把該節點存儲在堆棧，把堆棧的頂節點覆蓋，并根據每個節點的量度進行完全排序，使較快回到全零狀態的節點排在棧頂，為下一次的分裂做好準備。排序的目的主要是為了分裂較快回到全零狀態的節點。如果當前的節點到達樹的終點且節點的碼重未超過設定的上限，則存儲該節點至另一塊內存空間。如果存儲的節點狀態點到達了全零且碼重不大于設定上限、節點的數目小于設定的存儲數目，總的計算量小于Clim，則繼續分裂節點；否則，輸出存儲的節點。

該算法能夠停下來的二個條件：

（1）存儲滿足條件的節點等于設定的數目；

（2）總的計算量超過了Clim。

一旦該算法滿足上述結束條件，該算法就停止。只要是一個堆棧，堆棧的容量是確定的，就有可能出現堆棧滿的情況。考慮到存放在堆棧底部的節點被選擇作為最優路徑上的節點的可能性非常小，通常在堆棧滿的情況下，用堆棧頂部的進行0分裂的節點覆蓋當前的棧頂節點，而進行1分裂后的節點覆蓋堆棧底部的節點。因此，該堆棧成為首尾相連的循環堆棧。每進行一次分裂都要進行排序。為了方便排序和堆棧的棧頂指向，需要設置一個堆棧指針始終指向棧頂。由于排序需要耗費大量的時間，堆棧的長度不易較大。為了使碼樹能夠充分分裂，堆棧的長度也不易過小。綜合以上兩方面考慮，堆棧的大小應該根據卷積碼的約束長度取一個較為合適的值。利用該搜索算法找到的部分具有較大約束長度的卷積碼如表1所示，其中生成多項式使用十六進制表示。

3 仿真測試

卷積碼的性能必須通過加噪聲的信道進行檢驗，以檢驗編碼器在不同信道比條件下的誤碼率。采用費諾譯碼算法在受擾信道中檢驗，以測定大約束長度卷積碼在噪聲干擾情況下對誤碼率的改善情況。圖2給出了約束長度為60和32的大約束長度卷積碼在不同信噪比下出現錯誤幀的概率。可以看出，當約束長度固定時，隨著信噪比的增加，錯誤幀的概率降低；當信噪比固定時，隨著約束長度的增加，錯誤幀的概率明顯得到改善。

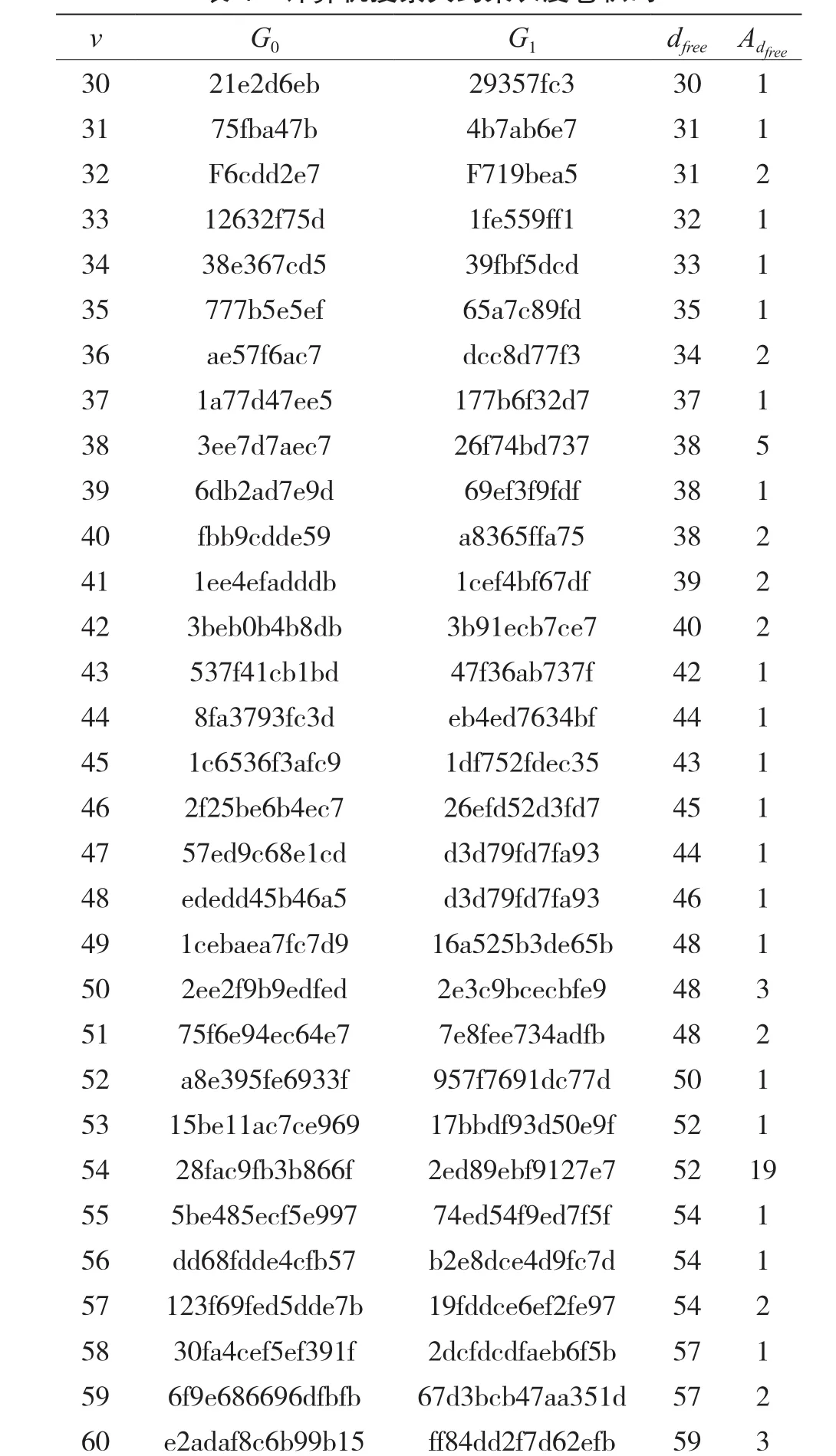
表1 計算機搜索大約束長度卷積碼

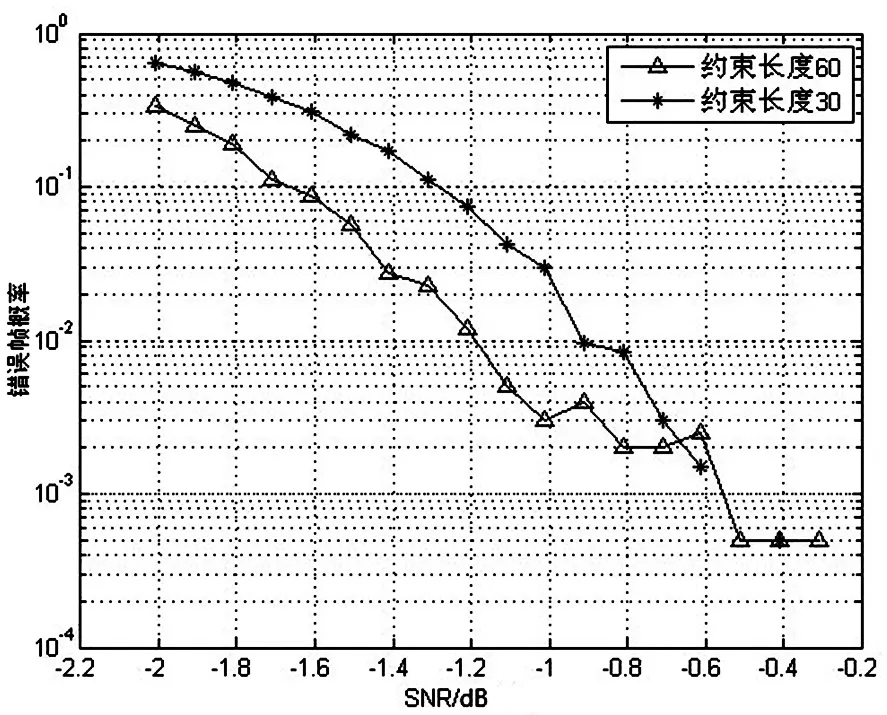
圖2 不同信噪比下不同約束長度卷積碼性能對比

4 結 語

本文提出了一種改進的大約束長度卷積碼搜索算法，利用該搜索算法可以找到約束長度大于30的卷積碼編碼器。利用費諾譯碼算法對不同約束長度的卷積碼編碼器的性能進行檢驗，結果表明，通過該搜索算法找到的大約束長度卷積碼的在同等信噪比的情況下的誤碼率較低。