滑坡受災結構體易損性離散元分析

畢鈺璋 孫新坡 何思明 王安輝

（1.東南大學交通學院巖土工程研究所，江蘇南京210096；2.四川理工學院土木工程學院，四川自貢643000；3.中國科學院山地災害與地表過程重點實驗室，四川成都，610041；4.中國科學院·水利部成都山地災害與環境研究所，四川成都，410041；5.中國科學院青藏高原地球科學卓越創新中心，北京，100101）

1 項目背景

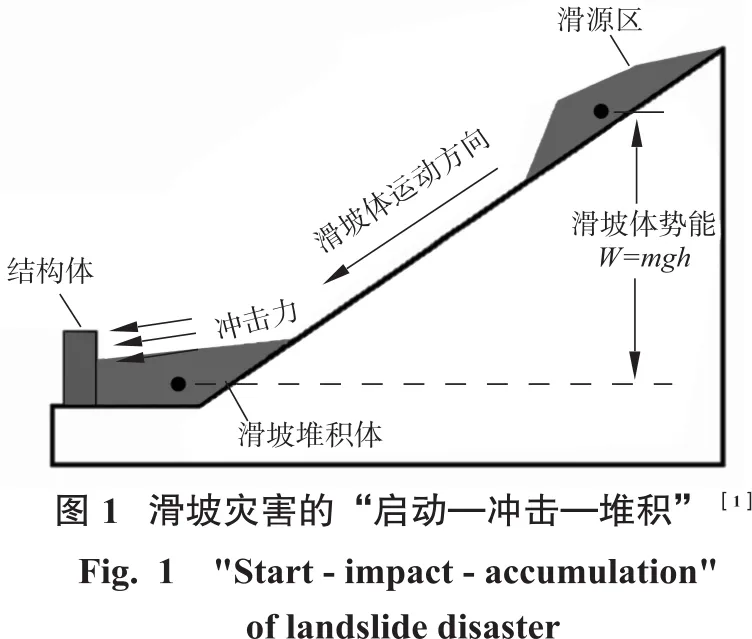
滑坡災害是工程地質中的一種常見的災害形式，其中又以高速遠程滑坡的破壞程度尤甚，它的運動過程伴隨著巨大的動能并且對所經過的結構體造成了巨大的沖擊和破壞［1-2］，圖1中顯示的就是滑坡災害從發生到沖擊結構體直至堆積的整個過程的示意圖［3］。滑坡災害體對結構體的沖擊作用以及破壞程度在地質災害的研究領域中一直被認為是評價災害程度的一個重要指標。傳統的滑坡災害的風險研究當中通常用災害體滑移的速度及其運動的距離來作為評判災害破壞程度的一個重要標準。然而在現實的滑坡災害案例中，災害的破壞程度往往取決于其對居民區的房屋建筑、道路、橋梁等結構體所產生的破壞程度［4］（見圖2）；而研究災害體和結構體之間的動力響應則屬于滑坡易損性的研究范疇：各國學者已經證明了易損性分析可以預測結構體在遭受不同滑坡災害體的作用下發生各級破損的概率，對于擋土墻以及抗滑樁的設計、加固和維修決策具有重要的應用價值［5-8］。

在研究滑坡易損性的過程當中，實證分析、實驗模擬和數值計算是我們3種常見的做法。國內外學者對此做出了大量的工作：Mileti團隊以哥倫比亞的Nevado Del Ruiz災害為實例分析了災害體和建筑物的動力響應［9］。Toyos在研究Vesuvius的某次滑坡災害中提出了可以系統地評估建筑受損程度的一套方案［10］。M Silva［3］通過實證研究提出了評價災害易損性的3個指標：結構體的抗破壞程度（BR），滑坡的規模（LM）以及結構體的經濟價值（EV），并提出了一套完整的災害損失評價方法。Shi［11］通過離散元數值模擬的方法研究了不同摩擦系數條件下滑坡體與結構體的動力響應過程，并給出了摩擦系數與判定災害易損性的相互關系。雖然前人做了很多相關的研究工作，但大部分工作仍停留在宏觀的范圍，給出的評判災害損失的方法與真實的損失仍存在一定的差異。雖然有學者研究了災害體和結構體之間的動力響應關系，但大部分沒有考慮實際情況，比如有學者考慮了坡面摩擦系數與災害易損性之間的關系［11-12］，然而現實的災害發生過程中，災害體滑動時其坡面的摩擦系數大體是不變的。

相對于基于坡面摩擦系數的結構體易損性研究，筆者認為基于災害體破碎程度的結構體易損性研究更具有實際的工程意義。圖3顯示了不同破碎程度的滑坡體對結構體的沖擊示意圖。Iverson指出在泥石流、碎屑流等災害體中不同的顆粒級配會對其流動性產生很大的影響［13-14］，Jiang通過實驗驗證了這一理論并給出了不同顆粒尺寸條件下災害體的運動機理，并指出顆粒之間的摩擦系數以及顆粒本身的尺寸大小是影響其運動機理的主要原因［15-16］。基于此，本項目致力于研究滑坡體破碎程度對其破壞程度的影響，通過探究不同破碎程度的滑坡體和結構體之間的動力響應來得出相應的規律性的結論，并通過這些結論完成基于滑坡破碎程度的易損性的評價。

2 滑坡破碎程度和易損性評價的關系

在眾多的易損性研究中，最主要的研究方法包括概率統計法和易損性評估法——這些方法的主要研究手段是工程實例分析［17-18］。如圖1所示，在離邊坡坡角的一定距離是一個結構體，它所受的破壞程度取決于邊坡的幾何形狀及其地質條件；然而即使是在相同的邊坡條件下，不同類型（形狀、材料）的結構體將很可能受到不同程度的沖擊和破壞。因此，結構體的最終破壞程度將取決于災害體及結構體本身的共同作用——這就意味著在災害風險評估中僅僅分析邊坡穩定性是遠遠不夠的，結構體的破壞程度應當在易損性的研究中被充分考慮進去。在滑坡災害中，災害體的沖擊力和其滑動速度呈正相關，并且與其滑坡體的破碎程度有關。

在結構體設計的過程中，其受到災害體沖擊破壞時的臨界值通常是判別結構體“可靠”和“不可靠”的非常關鍵的因素，并且需要大量的統計數據對其進行理論支持。然而，當隨機變量不服從正態分布時，極限狀態方程是非線性，這就給易損性的判定帶來了不便。鑒于破碎程度對滑坡災害的程度影響，式（1）給出了一個簡單的判別方法：

其中，S是災害體施加在結構體上的外部載荷的總和；F是結構體本身的強度；f代表影響滑坡災害體的破碎程度的系數——用災害體的當量沖擊力和結構體抗沖擊強度的比值來表示。如圖4所示：當f大于1時，結構體破壞；當f介于0和1之間，結構體保持穩定。

3 離散元方法的基本思路

離散元方法是基于分子動力學（molecular dynamics）而發展起來的一種方法。之后Cundall于1971年提出了適用于巖土力學的離散元方法［19］，并于1979年和Strack［20］在共同創立的一種基于二維圓盤和三維圓球排列建立數值模型的方法（PFC-2D/3D），其分析具體問題時整個模型的構建是主要以離散的“球（圓盤）單元”、以及“墻單位”組建起來的。其顆粒流模型的假設包括以下幾個方面：

（1）球體被視為剛性體。

（2）接觸發生在幾近非常小的一個范圍。

（3）接觸部分允許有疊加并且其接觸行為假設為“柔性接觸”。

（4）疊加部分遵循接觸力的“力—位移”法則。

（5）顆粒間的接觸允許有粘結。

（6）所有顆粒都是球體（圓盤）形狀。

本次滑坡易損性的數值模擬研究運用了二維離散元方法，基于PFC-2D的平臺，對不同破碎程度的滑坡災害進行了詳盡的研究。本次研究過程中使用的模型是“滑動模型”，它允許顆粒在抗剪強度范圍內發生滑動。滑動模型是通過兩接觸體間最小摩擦系數 μ定義的，如果顆粒之間重疊量Un小于或等于零，則令法向和切向接觸力等于零。發動滑動的判別條件為：

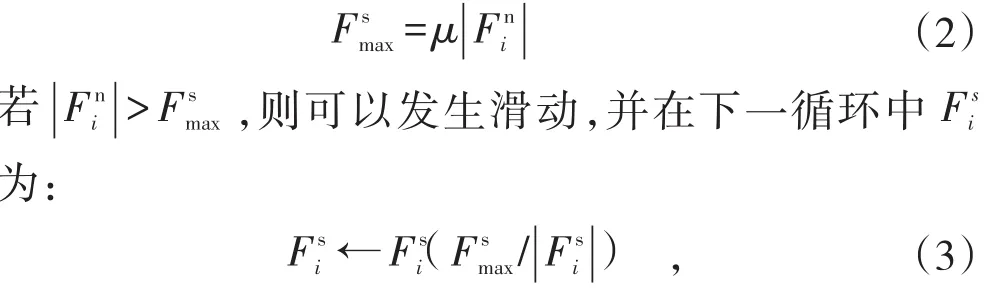
4 工程算例及模型建立

本項目采用了云南省肩輿山的一處典型的高陡滑坡（Palankeen Mountain landslide）來作為本次研究的工程算例［11］。該處滑坡為一處典型的高速滑坡，如圖5所示，該滑坡位于一個溝谷上方的斜坡帶：該溝谷處的邊坡坡角低至27°，高至48°，坡角值在這個范圍內波動；并且大部分地段出現了大于45°的陡坡情況。邊坡的整體形態呈不規則的近橢圓形態：沿公路的走向長度接近80～90 m，沿坡體下滑方向的長度接近250 m；邊坡后緣的高程約2 745 m，前方斷裂啟動處的高程約2 600 m，兩者之間的高程差約為145 m。該處滑坡為節理裂隙化的巖土體滑坡，現場調查的災害體主要由大量碎石組成，并包含有一定量的“粘土—礫石”混合物。整個滑坡的平均厚度為15 m，其總的滑坡體積大約為3.8×105m3。

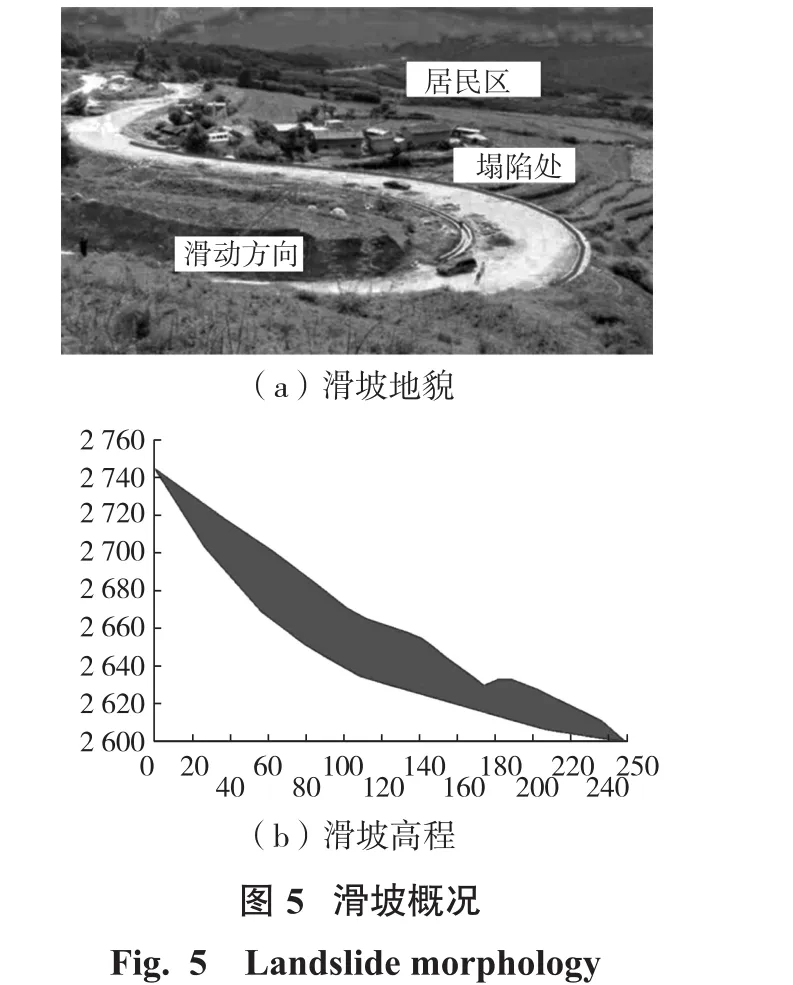
如圖6所示，圖中表示的是在PFC2D中生成的理想滑坡模型：模型的尺寸嚴格按照圖5中的尺寸建立，災害體由顆粒模型組成，坡面由“墻單元”組成。為了實現不同破碎程度的災害體模型，在相同體積災害體的條件下，采用不同大小的顆粒粒徑來表示其破碎程度：0.3 m、0.5 m、0.8 m、1.0 m。本次模型的建立分為3個步驟完成：研究所用模型的設定、數值模擬中的滑坡災害體的參數選取、數值模擬中的邊坡坡面的參數選取。

4.1 研究所用模型的設定

滑坡的真實剖面形狀和幾何尺寸如圖5所示，然而在本次研究過程中，筆者對滑坡的模型做了一個理想性的假設：假設邊坡滑移面底端到結構體之間為水平的地形條件（如圖7所示）。由于本次研究的目的是滑坡破碎程度對其易損性的影響，因此忽略復雜的地形條件有利于抓住研究過程中的主要矛盾，并且對原始地形模型進行的簡化有助于對模擬的結果進行定量化的對比，比如災害體的運動距離等。

如圖7所示，結構體距離坡腳處的距離為L，滑坡的高程為H，假設結構體高度h足夠高并且可以攔截所有的滑坡體——本次研究所采用的h為40 m。該處災害體在重力作用下滑移，對此我們進行了兩種不同條件下的模擬：如果L小于災害體的滑程，則災害體將對其滑程范圍內的結構體進行撞擊；如果L大于災害體的滑程，則不同條件災害體的動能將反映在其運動距離上。通過研究災害體的滑程及其和結構體之間的動力響應情況來綜合判定不同破碎程度下的滑坡災害的運動規律。

4.2 數值模擬中的滑坡災害體的參數選取

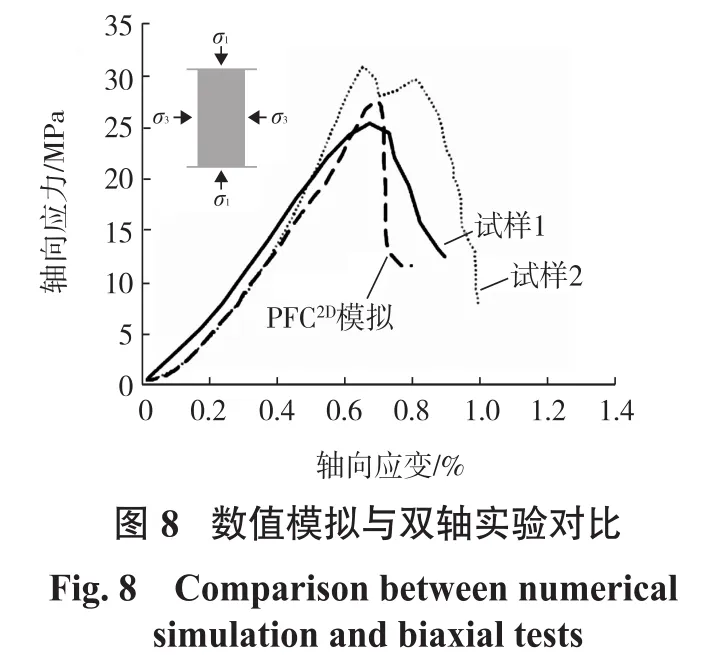
在離散元方法中，材料的宏觀運動行為取決于顆粒間接觸的微觀力學參數。然而對于參數的選取卻沒有一個完全有效的方式。較多的研究方式是通過物理模型和數值模型的破壞模式相匹配，從而確定其力學參數。由于沒有完備的理論依據來確定宏觀條件下的運動過程和顆粒力學參數之間的選取關系，因此我們在前人對該滑坡研究時參數選取的基礎上，通過反復的雙軸壓縮數值模型實驗（見圖8）來觀測應力-應變曲線，以期使其與實際的物理實驗相匹配。本次模擬過程參數的選取主要通過2個途徑來獲得：①來源于前人的參數，Shi［11］在使用離散元方法研究該處災害的同時，對災害體的參數進行了詳細的反演；②通過數值模擬雙軸壓縮試驗的方法對其中的一些參數進行了修正。表1為本次研究中所使用的力學參數。

4.3 數值模擬中的邊坡坡面的參數選取

眾多學者在研究滑坡災害的過程中，喜歡將邊坡坡面的摩擦系數考慮進去，從而研究不同坡面摩擦系數對滑坡災害體運動距離的影響；然而在大多數情況下，邊坡坡面的摩擦系數是一定的——即自然條件下的坡面摩擦系數的主要決定因素是植被的覆蓋率。根據現場勘查和現場采樣，Bi［21］設計了圖9所示的試驗，讓滾石從試驗裝置的“自然坡面”頂端滑落，觀測并記錄滾石的運動軌跡，然后通過PFC2D反演參數，通過對比二者的滾石運動軌跡，進而得到“自然坡面”條件下的摩擦系數。

通過二者的運動軌跡對比可以發現，在PFC22DD的摩擦系數取值為1.2的條件下，室內試驗和數值模擬的運動軌跡是極其相似的（如圖10所示）。因此，在本次研究過程中，坡面的摩擦系數引用前人的研究成果，并將摩擦系數取值為1.2。

5 結果分析

本次研究分3個部分進行：首先將滑坡的運動路徑設定得足夠長，用以研究不同破碎程度的滑坡的滑程；然后在滑坡運動范圍內設置結構體擋墻（H的取值分別為0，20，50，80，100，150 m），用于攔截災害體，并研究災害體與結構體之間的動力響應情況。

5.1 災害體破碎程度對滑程的影響

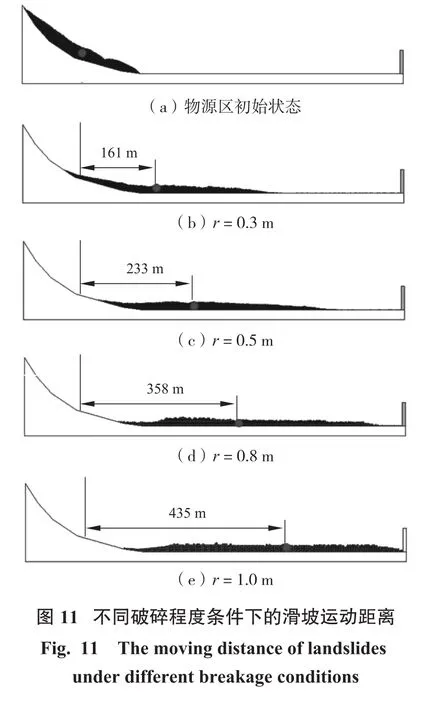
圖11顯示了不同破碎程度的滑坡在相同坡面條件下的滑移距離對比。通過圖11可以發現粒徑為0.3 m的條件下（圖11（a）所示），災害體重心的移動距離為161 m。隨著粒徑的增大，災害體重心的移動距離也慢慢增大。當粒徑達到1.0 m時，災害體的重心移動距離為435 m，幾乎為0.3 m粒徑條件下的3倍。通過對比發現：越是破碎程度較大的滑坡災害體，其流動性越差；越是塊體較大的災害體，其流動性越強。這是因為在災害體運動過程中，其內部的顆粒會相互碰撞，并耗散能量。在顆粒表面摩擦系數相同的情況下，顆粒越小，災害體被分割得越多，生成顆粒也越多，顆粒表面積總和越大，這就導致了摩擦耗散的能量越多。

5.2 不同破碎程度災害體和結構體之間的動力響應

圖12中顯示的是災害體顆粒粒徑r=0.3 m，結構體到坡腳距離L=0 m時，結構體上所受到的合力的變化。結構體上受到的力分為2個部分，即災害體對結構體的沖擊力（動力載荷）和災害體施加在結構體上的重力分量（靜力載荷）。在實際的滑坡災害中，由于結構體的破壞主要是緣于災害體總的合力的作用，動力荷載和靜力荷載共同作用并對結構體造成破壞，因此本研究主要考慮合力對結構體造成的影響，并不對2種力進行分解。

圖13中顯示的是在不同顆粒粒徑條件下，結構體和災害體之間的距離對結構體所受最大合力的影響。從圖中我們可以看出，在任何一組粒徑條件下，離災害體越近的結構體所受的合力的值也越大。我們用二次函數對其進行擬合，發現粒徑越大的災害體（破碎程度較低），其結構體所受合力隨距離L的變化程度越明顯：當r=1.0 m時，在L=0 m處的最大合力值與L=150 m處的最大合力值之差為5×107N；當r=0.3 m時，在L=0 m處的最大合力值與L=150 m處的最大合力值之差僅僅為1×107N。這是因為隨著結構體到坡腳的距離L值增大，災害體運動過程中的能量損耗不僅僅是顆粒之間的摩擦所造成的，顆粒能量耗散的過程可以分成2個階段進行：坡面滑動階段和水平運動階段。坡面滑動階段中，災害體從一定高度滑落到水平階段并將勢能轉變為動能，表現在微觀方面就是各個顆粒獲得了動能，在這個階段中顆粒開始獲得速度，而滑坡災害體整體能量的耗散主要是通過其顆粒內部摩擦來進行的。水平運動階段中，各個顆粒獲得了較大的動能，并向結構體方向運動。在這個過程中顆粒之間相互擠壓碰撞，這是導致滑坡災害體整體能量耗散的主要原因。由于顆粒越粗，其所組成的災害體的動能在坡面滑動的過程中能量耗散比較少（顆粒表面積之和小），故而在L=0 m的時候其結構體所受的最大合力值也越大。然而隨著結構體到坡腳之間的距離L值增加，大顆粒之間的碰撞、擠壓耗散的能量會相對于小顆粒更多，這也導致了從L=0 m到L=150 m之間的大顆粒所組成的災害體會耗散更多的能量。

圖14中顯示的是在不同結構體和災害體之間的距離L條件下，不同顆粒粒徑對結構體所受最大合力的影響。通過圖中曲線可以發現不管L的值如何變化，結構體所受最大合力和粒徑之間呈線性關系，具體變現：隨著粒徑地增大，結構體所受最大合力也呈線性關系地逐漸增大，即：F合=kr，其中k表示與L（結構體和災害體之間的距離）相關的耗能系數。L越大，則k值越小；L越小，則k值越大。

5.3 滑坡災害條件下的結構體表面應力分布

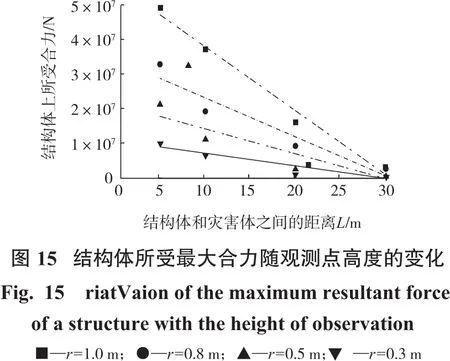
圖15中顯示的是在結構體所受應力隨觀測點高度增加而產生的變化。通過圖15中的曲線可以發現：在靠近結構體底端的觀測點測得的應力值要偏大，而在靠近結構體頂端的觀測點測得的應力值偏小；并且隨著觀測點從低到高，觀測點測得的應力值也由高到低分布，其分布規律接近線性分布。并且當粒徑r越大的條件下，結構體底部所受應力越大，其分布規律越接近于線性分布。圖16中顯示的是結構體受到災害體沖擊后，其表面上的應力分布情況。根據示意圖上的應力分布，在實際工程設計防護結構時，可以考慮將結構體底部的強度設計得更強一些，而結構體上部的設計可以根據實際情況和經濟條件進行適當的優化。

6 結論

（1）滑坡災害體的運動距離和其破碎程度呈反比；

（2）當災害體沖擊結構體時，結構體上所受的力（包括靜力和動力）和結構體與坡腳的距離L有密切聯系，具體表現為：F合=kr，其中k表示與L（結構體和災害體之間的距離）相關的耗能系數；

（3）災害體破碎程度直接影響了其能量的損耗方式：破碎程度大的災害體主要在滑坡啟動破碎階段通過顆粒間摩擦來耗損大量能量，破碎程度小的災害體主要在滑坡運動階段通過顆粒間碰撞來損耗大量能量；

（4）結構體受到沖擊后的表面應力分布滿足一個“三角形”，即頂端應力較小，底端應力較大，對于工程上的結構體設計具有一定的指導意義。由于本研究中的模型是建立在二維數值模擬平臺中，對實際問題進行了部分簡化，特別是在模型建立這個方面，所以為了得到更精確的結果，在后續的工作中應根據具體的地質條件建立三維模型并加以研究。