城市獨立坐標系下施工測量的簡化方法
楊 沖
(太原市市政工程設計研究院,山西 太原 030002)
為了方便開展城市測量工作,我國很多城市都建立了自己的獨立坐標系統。這種坐標系統具有變形小的特點,故很多大比例尺地形圖也是基于當地的獨立坐標系統而測制的。規劃設計部門也能很方便的在地形圖上進行城市的規劃設計工作。
但由于某些原因,很多地區的獨立坐標系統在建立時,并未選擇抵償高程面(或當地平均高程面)作為投影面,導致了地形圖上量得的距離與實地測量的不一致。這個問題在規劃設計階段尚不明顯,但在施工測量過程中影響很大。因此在實際測量工作中,必須考慮空間邊長的歸算問題。
以某市為例,當地測繪局在建立該市獨立坐標系統時,以54橢球(克拉索蘇斯基橢球)作為參考橢球,中央子午線選在該市中心區域,而將投影面選在了海平面(h=0)上,城區平均高程h平均=800 m。顯然,在該坐標系統下進行施工測量工作,將產生很大的變形,必須進行距離歸算,如圖1所示。
我們知道,空間邊長的歸算包括如下幾個過程:
1)將空間邊長d歸算為測線平均高程面上的長度Sm。
(1)
2)將測線平均高程面上的長度Sm歸化為橢球面上的弦長S0。
(2)

3)將橢球面上的弦長S0歸化為大地線長S。
(3)
一般城市測量中,因距離較短(在邊長為10 km情況下,此項改正僅為1 mm),故不考慮第3)項改正,即:
(4)
得距離改正值ΔS:
(5)
其中,Hm為測線高出投影面的高度;RA為A點沿測線方向的法截線曲率半徑。
畢竟,設計工作不可能在橢球面上進行,必須通過高斯投影將測量數據投影到平面上,高斯投影改正公式如下[1]:
(6)
在不影響短距離精度計算情況下,忽略第二、三項,得:
(7)
將式(4)代入式(7)得:
(8)
由式(5)和式(8)得,測線長度歸算到高斯平面上的改正公式:

(9)
其中,ym為測線兩端點橫坐標平均值;R為地球平均曲率半徑,取6 371 km。
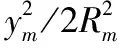
(10)
代入Hm=800 m,R=6 371 km,有S高斯=0.999 874Sm。
由此可以得出,當城市獨立坐標系的投影面不是測區平均高程面時,在小范圍城市測量工作中,測量距離改正可只考慮地面點高程帶來的影響。這時,只需將全站儀測距的比例常數調整為R/(R+Hm),即可直接用于施工控制測量。

