考慮支路可靠性過程的網絡節點狀態仿真

張 璇

(天津泰達電子工程有限公司 天津 300450)

0 引 言

電力系統可靠性是通過定量的可靠性指標來衡量的。在一般性的可靠性分析方法中，電力系統的可靠性指標——故障率λ、故障修復時間 t及年停電時間u等均由元件的基本可靠性指標求得。在這里就出現了一個近似條件，即認為當支路(設備)狀態變化滿足齊次馬爾可夫過程特點時，節點狀態變化同樣滿足，所以才有了通過支路(設備)可靠性指標去求節點指標的各種方法，但其中網絡節點的狀態變化是否符合條件并未有相應的解釋。

因此，本文擬應用計算機軟件，在不考慮容量約束的情況下，通過仿真設備(支路)的狀態變化對網絡節點狀態的影響，來判斷節點狀態變化是否符合或者近似符合齊次馬爾可夫過程。

1 網絡節點與支路狀態的可靠性分析方法

1.1 馬爾可夫(Markov)過程簡介

可修系統模型是一種重要的可靠性模型，因其引入了允許設備修復的概念，使系統可靠性研究得以更加完善。假定設備的故障率λ和修復率μ均為常數，則各部件的故障分布和修復時間分布均為指數分布，在這種條件下，總可以找到適當的系統狀態，以使用馬爾可夫過程描述[1]。基于馬爾可夫過程的這類可修系統是可靠性分析中研究及應用最多的一類系統。

1.1.1 馬爾可夫過程的定義

則稱隨機過程{ X (t), t ≥ 0 }為連續時間、有限狀態空間的馬爾可夫過程。

若對任意t，u≥0，均有：

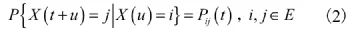
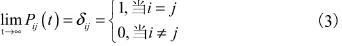
若用Pj(t)表示t時刻系統處于狀態 j的概率，則：

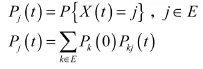
對于此處描述的有限狀態空間 E的齊次馬爾可夫過程，以下極限存在且有限。

1.1.2 馬爾可夫可修系統模型

存在一個可修系統，在t時刻所處的運行狀態可以用 X (t)來表示。該存在N+1個運行狀態，其中狀態 0，1，…，K是系統的正常工作狀態；K+1，…，N是異常故障狀態。記假定所表示的馬爾可夫過程為齊次的，且在足夠小的時間Δt內的轉移概率函數滿足：

顯然：

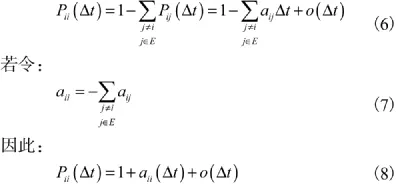
則由式(4)可知：

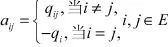
在系統的可靠性分析過程中，各類可靠性指標就可以通過上述齊次馬爾可夫過程的一般應用模型來求得。

1.1.3 系統的可用度

系統在任意時刻t，處于可用狀態的概率稱為系統的可用度。下面對用馬爾可夫過程分析可修復系統瞬時和穩態可用度的方法及過程作一些介紹。

①瞬時可用度

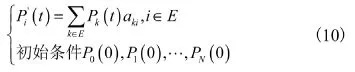
公式(10)可以寫成矩陣的形式：

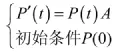
②穩態可用度

系統的穩態可用度是評估系統可靠性的重要依據，與瞬時可用度相比，工程實踐更加注重系統的穩態可用度。可以運用 P (t)的極限分布來求得系統穩態可用度，此處引用以下結果[2]。

由式(5)和(8)，可知定理1的條件滿足。由于：

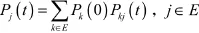
當t→∞時，根據定理1，上式右端極限存在，因而左端的極限也存在，且：

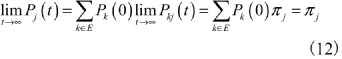
定理2，系統的穩態可用度為：

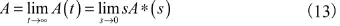
這樣，穩態可用度A就可以通過瞬時可用度A(t)來計算。

1.1.4 分析馬爾可夫型可修系統的步驟

給定一個滿足上述定義條件的具體的馬爾可夫型可修系統，可通過以下步驟求得系統的各項可靠性分析指標。①定義系統的狀態，并保證該狀態能夠完整地表示并區分系統的正常和故障運行情況。令為系統的狀態集合，分別表示系統正常運行狀態的集合和故障狀態的集合。②定義t時刻的隨機過程。若各部件的故障分布和修復時間分布均為指數分布，則該隨機過程是一個有限狀態空間E上的齊次馬爾可夫過程。③求轉移率矩陣A。對前面定義的隨機過程 X (t)，可以求得轉移概率函數：

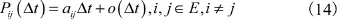
進一步寫出轉移率矩陣：

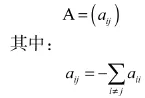
④求解 Pi(t)=P{X(t)=j}，j∈E。解微分方程組：

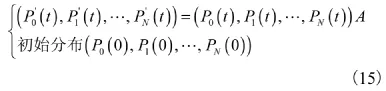
可以利用拉氏變換的方法，先將其轉化為線性方程組求解，再作反變換，得出微分方程組的解。⑤求系統的瞬時可用度和穩態可用度。由上述介紹可知：

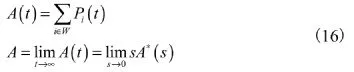
1.2 系統網絡可靠性的計算方法

系統節點可靠性的分析是在元件故障和修復數據以及系統結構的基礎上，求得的能夠表明系統可靠性的定量指標[3]。目前，研究系統網絡可靠性的基本分析方法主要有兩種：解析法和蒙特卡洛模擬法，下面分別予以簡要介紹。

1.2.1 解析法

解析法基于馬爾可夫模型，常用于一些簡化了的或小型的組合系統的可靠性評估，通過建立并求解電力系統的可靠性分析數學模型，從而計算得出系統的可靠性分析指標。

這種計算方法的優點在于利用了精確的數學模型，概念清晰，易于理解，且邏輯關系明確，模型的精度較高；其缺點是當系統規模較大時，計算量便會隨著系統復雜程度的增大呈現指數增長。因此解析法僅適用于系統網絡規模較小，元件數目不太多但故障時有重大影響的情況。

解析法中應用較為廣泛的主要有網絡法、故障樹分析法(Fault Tree Analysis)和狀態空間法。至于具體選擇何種方法，則需要根據系統結構和規模、元件的獨立性和可修復性、故障時間及修復時間的概率分布(指數或非指數分布)、故障模式(獨立、相關或共同模式故障)以及運行方式和環境的影響等[3]進行判斷。下面僅對本文算例中用到的狀態空間法進行簡要介紹。

系統某一時刻所處的狀態取決于系統中各元件的狀態。系統網絡中的元件一般為兩狀態元件：正常工作狀態或異常故障狀態。對于一個給定的系統網絡，可能出現的所有可能的狀態集，就稱為狀態空間，其中任何一個元件的狀態發生變化，都將使系統從當前狀態轉變為另一個狀態。

所謂狀態空間法，就是用系統所處的狀態和這些狀態之間可能發生的轉移來表示系統，并由故障判據劃分出系統正常工作狀態和故障狀態，以求得系統的可靠性指標[3]。

在元件的故障密度函數和修復密度函數服從指數分布的情況下，元件的故障率和修復率都是常數，便可以應用齊次馬爾可夫過程來描述系統的狀態變化，對其求解來得到各項可靠性指標。對于規模較小的系統網絡，狀態空間法的基本計算步驟如下：列舉出所有可能的系統狀態，并規定系統故障判據；根據元件的兩狀態概率計算系統處于某一狀態的概率；分析各狀態之間如何轉換，并根據計算出的轉移概率，畫出系統狀態轉移聯絡圖；按照規定的故障判據，將各種系統狀態進行分類(一般可靠性分析中只需將各種系統狀態分為正常和故障兩大類)，然后逐個檢驗其事故后果，針對某一類狀態計算系統的可靠性指標[4]。

本文所討論的“考慮支路可靠性過程的網絡節點狀態仿真”，針對具體問題所用到的狀態空間法的分析過程不盡相同。

1.2.2 電力系統可靠性評估的模擬法

模擬法又稱隨機抽樣方法，其本質思想就是一種概率模擬的方法：為了求解一個問題，首先建立一個概率模型或隨機過程，使它的參數等于問題的解，然后通過對模型或過程的觀察或抽樣實驗來計算所求參數的統計特征，最后給出所求問題的近似解，并給出解的精度或誤差[3]。蒙特卡洛模擬法的優點是模型簡單，省去了復雜的數學推導和演算，比較直觀，易于理解和掌握，因此該方法在電力系統可靠性評估中的應用得到了快速發展，并逐漸成為可靠性評估的重要方法[5-7]。

2 網絡節點可靠性仿真算例

2.1 仿真網絡模型介紹

本文所采用的仿真實例是由24個單元設備組成的網絡結構，其結構如圖 1所示。其中，A、B節點為電源節點，向網絡中供電，C節點為負荷節點。假設設備正常工作時為0狀態，故障時為1狀態。

從該網絡圖中我們可以得到如下信息：支路數14條；使負荷節點 C可以正常工作的所有最小路狀態容易得知。

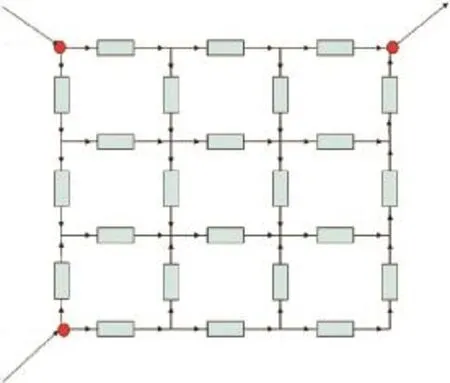
圖1 仿真網絡模型Fig.1 Simulation network model

仿真程序中的一個輸入變量即是這14個能夠使負荷節點 L正常工作的最小路的狀態，即只要在每個狀態中相應元件為 0，系統就可以正常工作，不論其他元件的狀態是 0或者 1。在仿真程序中，我們允許2個及以上設備同時發生故障。

對于每個單元設備，為了簡化分析過程，我們假定其故障率λ和修復率μ均相同，且為常數。用MATLAB軟件進行程序仿真。仿真程序的輸入變量為負荷節點能夠正常工作的最小路狀態集 P、系統運行時間T以及設備數量N。輸出變量STA為負荷節點L在所有運行時間中在每一段時間的狀態(0狀態和 1狀態)，以及系統在相當長一段時間內的穩態可用度A，同時還能夠生成穩態可用度A隨時間t的變化關系圖。

仿真流程圖如圖2所示。

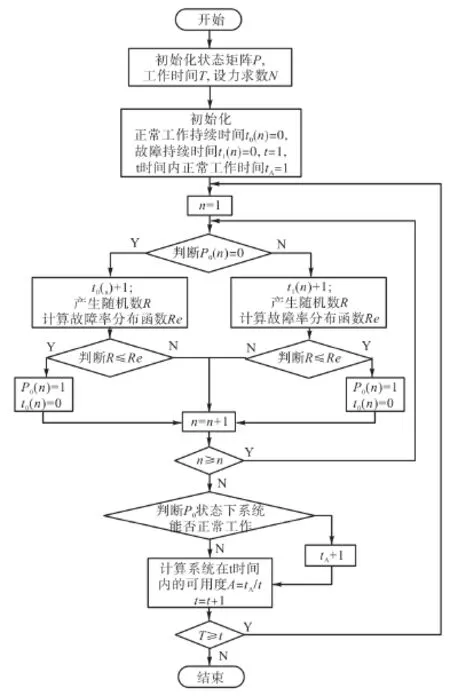
圖2 仿真流程圖Fig.2 Simulation flow chart

2.2 仿真結果統計與分析

仿真結果得到的系統穩態可用度 A的變化規律如圖3所示。

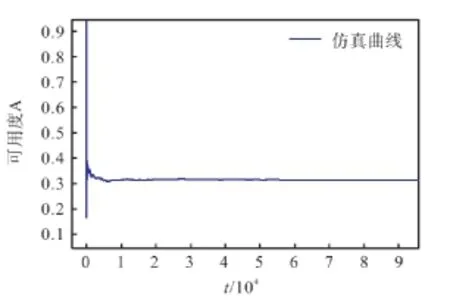
圖3 可用度變化曲線Fig.3 Availability change curve

從理論與實驗圖的對比中，我們可以看到，穩態可用度A隨時間t的變化分布規律是大致相同的。此外，在 t很小的時候，可用度 A在局部有小的波動，而由理論值得到的圖是十分標準的呈 e的負指數次冪衰減的曲線。

3 結 論

在一般性的可靠性分析方法中，網絡節點的可靠性指標——故障率λ、故障修復時間r及年停電時間u等均由元件的基本可靠性指標求得。針對許多實際應用中直接假定網絡節點的狀態變化與設備狀態變化規律相同，都滿足齊次馬爾可夫過程而未加證明的問題，本文作了相關研究和討論，得到以下結論：在設備(支路)的狀態變化滿足齊次馬爾可夫過程的條件下，網絡節點的狀態變化也基本滿足齊次馬爾可夫過程的假設是成立的，并且偏差數值在可接受的范圍之內；以往計算中所假定的情況，根據齊次馬爾可夫過程的計算條件，在每一個tΔ的計算時間內，最多只有 1個設備發生故障，但由實驗結果可以看到，在允許2個及以上設備同時發生故障的情況下，所得到的網絡節點可用度依然按照 e的負指數次冪衰減的曲線規律變化。因此，在實際的可靠性評估計算中，為了簡化工作量，可以將2個及以上設備同時出現故障的概率認為是零，這對于評估結果不會產生較大的影響，可以得到相對準確的可靠性指標。