含有時滯控制的準零剛度隔振器動力學分析

李東海, 趙壽根, 何玉金, 李 濤

(北京航空航天大學 航空科學與工程學院， 北京 100083)

振動隔離是解決工程振動問題的重要手段。在目前大量的工程實際中，普遍采用線性隔振器，對于一些精密儀器而言，如航天器上的光學元件，低頻振動對其精度影響更大。如采用線性隔振措施，勢必要降低隔振器的剛度從而實現低頻隔振。這也會造成隔振器的靜態穩定性降低。理想的情況是隔振器具有較高的靜態剛度來保證靜態負載能力，并且具有較低的動態剛度來增大隔振頻率范圍。高靜態剛度低動態剛度(High-Static-Low-Dynamic-Stiffness, HSLDS)特性可以通過非線性結構來實現[1]。Ibrahim[2]綜述了非線性隔振器的發展，表明非線性隔振是一個十分活躍的領域。Liu等[3]在其綜述中也詳細地闡述了非線性隔振器在微振動隔離領域的應用。Yang等[4]研究了帶有負剛度機構的非線性隔振系統的動力學行為。研究表明增加負剛度機構能極大地擴展隔振頻帶，并且非線性隔振系統的功率流特征結果也表明增加負剛度能使系統具有更好的隔振性能。Shaw等[5]用雙穩板來制作輕而有效的高靜態低動態剛度的隔振系統，可以采用非線性剛度元件來實現準零剛度(Quasi-Zero-Stiffness, QZS)特性[6]。彭獻等[7]采用連桿機構作為負剛度調節機構，研究了準零剛度隔振器的設計方法。Zhang等[8]將歐拉壓桿作為負剛度調節機構，設計了正負剛度并聯的隔振系統。Carrella等[9-12]利用斜置彈簧產生負剛度特性，并與正剛度彈簧相并聯組成準零剛度隔振器，并詳細地研究了隔振器的靜動態特性。Xu等[13]利用電磁彈簧作為負剛度元件，設計了一種準零剛度隔振器，其隔振性能在低頻區域，超過了等價的線性隔振器。由于準零剛度具有高靜態剛度低動態剛度，可以有效地克服傳統非線性隔振器增加隔振頻率范圍和保證靜態承載力之間的矛盾，近年來，針對準零剛度隔振器的研究變得越來越熱門。

準零剛度隔振器有著線性隔振器不可比擬的優點，那就是隔振頻率范圍廣，靜態剛度高。但是相比線性隔振器而言，其共振峰值依然被認為是過大；由于準零剛度隔振器的固有的非線性，所以會造成系統的跳躍現象，這種系統的不穩定性是一種不安全因素所以在工程實際應用中不期望出現的。因此為了獲得更好的隔振性能，開展準零剛度隔振器的主動控制策略的研究就顯得十分必要了。準零剛度隔振器的動力學特性方程可以用具有三次非線性項的Duffing振子模型來描述[14-17]。目前針對準零剛度隔振器的主動控制研究相對較少，但是許多學者開展了對Duffing振子和吸振器的主動研究[18-21]。在吸振器的主動控制研究中，學者主要采用了時滯控制的策略，這是因為在實際應用中，控制器和作動器會有不可避免的時間滯后，所以在研究控制策略的時候，將時滯效應納入考慮范圍之中。Zhao等[22]將時滯控制策略應用于雙自由度非線性吸振器中，來抑制垂直位移方向的振動，其研究成果表明，采用時滯正反饋的非線性吸振器可以有效地抑制大約65%的垂直振動，而采用負時滯反饋的吸振器可以吸收86%的振動。但是針對準零剛度隔振器的時滯控制研究相對較少，本文在之前的研究基礎上，對準零剛度隔振器施加線性位移時滯控制，并對其靜力學特性進行分析，在力激勵的情況下，利用平均法對隔振器的動力學特性進行理論推導，并分析了隔振器增加時滯控制后的穩定性，以及發生跳躍現象和Hopf分叉現象的臨界條件。

1 準零剛度隔振器動力學模型

1.1 準零剛度隔振器

本文采用兩個斜置彈簧作為負剛度元件與豎直的正剛度彈簧相并聯形成單自由度的準零剛度隔振器。對其進行線性時滯位移主動控制的結構模型如圖 1中，當隔振器受載后，斜置彈簧處于水平位置并達到靜平衡點處。其長度為l。自由狀態時，此時質量m距離靜平衡位置的距離為xs；x為負載質量m從靜平衡位置開始的位移。斜置彈簧的原長為l0。斜置彈簧的剛度為kh，垂直彈簧的剛度為kv，假設系統的阻尼為線性阻尼，阻尼系數為c，控制剛度為kc，反饋信號為系統的線性位移x；f為負載質量m受到的外界激勵力。

1.2 準零剛度隔振器動力學分析

準零剛度隔振器線性位移時滯控制結構示意圖如圖 1所示。為了建模的簡便性，先考慮無控制系統的動力學特性。利用拉格朗日方程可以建立準零剛度隔振器的動力學方程。

圖1 準零剛度隔振器線性位移時滯控制結構示意圖

隔振器的動能為

(1)

現設靜平衡位置為系統的勢能零點，則該系統的總勢能為

(2)

拉格朗日函數可以表示為

(3)

拉格朗日方程表示為

(4)

式中：F(t)為隔振器受到的外界激勵力；t為時間。

聯立式(3)和式(4)可得到隔振器的動力學微分方程

(5)

引入無量綱參數，可對式(5)無量綱化，得到隔振器的無量綱動力學方程

(6)

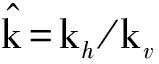
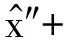
(7)

當隔振器的響應位移相對初始垂向長度為小量時，可以將系統的動力學方程在靜平衡點處展開并保留三次精度，將系統的動力學方程轉化為類似于Duffing方程的形式來研究。對式(6)應用泰勒展開并保留三階精度，得到

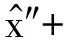
(8)

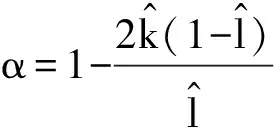
(9)

由式(9)可以清晰地看出來，系統具有三次非線性項，可以利用Duffing方程的部分特性來研究其特性。

2 簡諧力激勵下的系統的響應

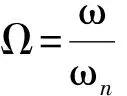
(10)

(11)

在式(11)中

將ΩT+θ在0-2π之間取平均值[23]得到

(12)

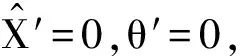
(13)

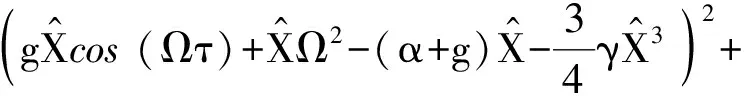
(14)

相頻特性為

tanθ=

(15)

為了更清楚地分析線性時滯位移反饋對系統動態響應的影響，定義受控系統的等效阻尼系數和等效線性剛度比分別為

(a) 幅頻響應曲線(b) 相頻響應曲線

(a) 幅頻響應曲線(b) 相頻響應曲線

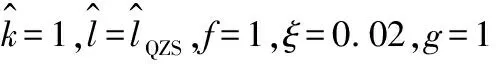
(16)

αeq=α+g(1-cos (Ωτ))

(17)

當g=0，sin (Ωτ)>0時隔振器處于不受控狀態，隔振器主振動共振峰值響應很大，而當g≠0，sin (Ωτ)>0時，共振峰值被有效地抑制，這種現象也可以在圖 2中體現出來。這就很好地說明了線性位移時滯反饋的阻尼效應。而當sin (Ωτ)<0時，系統的等效阻尼減小，共振峰值相比不受控系統增大。

(18)

αeq=α+g(1-cosτ)

(19)

這樣可以近似認為在共振區域內，等效阻尼比和等效線性剛度比是周期為2π周期函數。因此時滯參數τ的取值范圍為τ∈(0,π)，在該范圍內系統的等效阻尼總是大于不受控系統的阻尼。

3 準零剛度隔振器穩定性分析

(20)

可得系統的擾動方程為

(21)

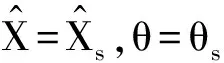
系統的穩定性可以通過線性擾動方程式(21)的特征方程來分析

(22)

當a1>0，a2>0，則奇點漸近穩定；當a1>0,a2<0時，奇點不穩定。所以a2=0為穩定性邊界。注意到a1的取值和系統的非線性項無關，實際上a1代表著有控制時線性自由振動的穩定性，穩定性獨立于激勵、響應幅值等。當a1=0意味著特征方程會有一對純虛根出現，因此會出現Hopf分叉[26-28]。

由a2=0可得穩定性邊界為

(23)

其中a=gcos (Ωτ)+Ω2-(α+g)；b=gsin (Ωτ)+2ξΩ

(24)

(25)

(a) g=0(b) g=1

(a) τ=0(b) τ=π6

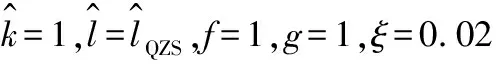
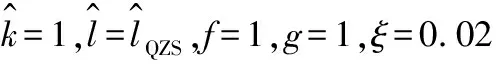
(26)

為了更加直觀地說明(f,g)的取值對隔振器跳躍現象的影響，可取不同的(f,g)繪圖說明。當(f,g)的取值為(0.4, 0.1)時，處于區域2中，隔振器不會發生跳躍現象；當(f,g)的取值為(0.4, 0.3)時，處于區域1中，系統會發生跳躍現象。隔振器的響應曲線如圖 7所示。

圖時跳躍現象臨界曲線

(a) (f,g)=(0.4,0.1)(b) (f,g)=(0.4,0.3)

圖7 當無量綱外界激勵力的幅值f和控制增益參數g處于區域1和2中時隔振器的響應特性

Fig.7 The response characteristic of the isolator when non-dimensional excitation amplitudefand control gain g are fixed in region 1 and 2 respectively

由臨界條件a1=0得到

gsin (Ωτ)+2ξΩ=0

(27)

可以得到在參數(g,τ)平面內Hopf分岔的邊界。對于自由振動的線性系統，其幅頻特性為

(28)

將式(27)代入式(28)中，得到

gcos (Ωτ)+Ω2-(α+g)=0

(29)

將式(29)與(27)聯立，得到頻率比和臨界時滯參數的表達式如式(30)所示。式(30)所控制的曲線為系統發生Hopf分岔的邊界。

(30)

如圖 8所示為Hopf分叉的邊界曲線。當(g,τ)取值在參數平面A中，則特征方程式(22)的特征值的實部為負，系統的運動隨著時間衰減；當(g,τ)取值在參數平面B中，特征值的實部為正，系統會作由Hopf分叉引起的周期振動，造成系統平衡點的不穩定；而當(g,τ)取值恰好位于曲線之上時，特征值的實部為零，為發生Hopf分叉的臨界條件。

圖時的Hopf分叉臨界曲線

4 結 論

本文研究了含有線性位移時滯控制的由三彈簧組成的準零剛度隔振器在簡諧力激勵下的動態響應與穩定性特性。通過李雅普諾夫線性近似穩定性理論和勞斯-赫爾維茨準則研究了系統的穩定性和系統的跳躍現象以及Hopf分叉現象，理論分析表明，在系統發生跳躍現象的頻率帶內，為系統的不穩定區域，同時給出了系統的穩定性邊界。在此基礎上討論了該類型隔振器系統增加時滯控制時的動力學特性，結果表明有線性位移時滯控制時可以有效地抑制系統響應幅值，同時進一步研究了時滯參數與控制增益對響應的影響，定義了等效阻尼和等效線性剛度系數，給出了時滯控制參數的取值范圍，討論了時滯控制對系統的阻尼和剛度的影響，從研究和討論得到的結果看出準零剛度隔振器在給出控制參數的范圍內，受控系統的動力學響應特性比不受控系統性能更為優越。