高層建筑物變形監測數據分析研究

□ 張錦根

（福建省國土測繪院，福建 廈門 361012）

0.引言

高層建筑物增高和載荷參數性質存在差異性，受地下根基和地上材質與構造共同影響，建筑物會產生下沉，嚴重的情況下，建筑物會發生傾斜產生縫隙，影響正常使用，如果情況很嚴重，將威脅人們生活財產安全。因此，我們必須重視高層建筑物的穩定性。變形預測是建筑工程的重要研究問題之一，是防災減災防患于未然的關鍵。高層建筑變形監測研究中一個關鍵步驟是沉降觀測，利用傳感器和測量等技術獲取建筑沉降值，探究建筑物變形內在聯系，獲得變形規律，再用合理的方法對建筑物沉降變形大小進行預測，以便根據需要及時采取適當的預防或善后措施，確保建筑物的安全使用。本研究充分考慮建筑物沉降變形的復雜性和多樣性，尋找最優模型來逼近、模擬和揭示沉降變形的規律和動態特征，借助數學回歸分析方法預測建筑物的沉降變形，對建筑物的修建和保養管理與防災減災具有重大意義。

通過多期監測數據的計算與分析處理，及時反饋和發現施工過程中不均勻沉降的發展情況，并且將監測的結果用于信息化反饋，以確保施工過程中的優化設計，保證主體結構的穩定安全。由于通常間接平差和條件平差，都是將基準點設定為固定量，在有些特殊的環境中，歪曲度觀測會受干擾，從而影響到監測的精度，例如在有些建設施工處，基準點距離建筑物很近而且在較淺土層中，如果有重型車輛經過或是施工時，這些基礎點會受到地面震動的影響。理論上，實際基準網存在穩定和不穩定變量，對基準網做自由網平差，然后使穩定未知量擬合于它們的穩定值，使在穩定狀況下，達到不歪曲監測的目標。

1.工程概況

廈門市某建筑大廈，占地面積為4.3畝，建筑面積為42338平方米，用途類型為商住，主體層數為29。大廈地基土屬于軟土地基，由于在大廈附件修建地鐵時為了確保建筑物主體結構的安全穩定，在整個地鐵修建項目施工過程中，通過對大廈高層建筑物結構主體進行沉降監測，達到對產生危害建筑物不均勻沉降提前預警的目的。

監測建筑物沉降數據時，為確保基準點有關數據準確度，必須分期測定基準點的沉降情況，然后對各個點的穩定性進行檢驗，將差異性很大的離散點去掉，獲取穩定的點作為觀測基準點。在實際工作中很難確定水準網中哪些點是可靠的，哪些點不可靠，常應用數理統計法先總體檢驗基準點的穩定性，然后選定部分點檢驗穩定性。

本次試驗以第一次和二次觀測結果為研究對象進行數據分析，其余觀測結果均可按相同方法進行處理即可，觀測數據（如表1所示），表中為兩次觀測數據的高差，該數據中人為把距離為8定為單位權，高差變化為第二次觀測與第一次觀測的差值。

表1 某建筑沉降監測日報表 單位：mm

續：表1

通過MATLAB程序處理后得到的改正數及協因數（如表2所示）。

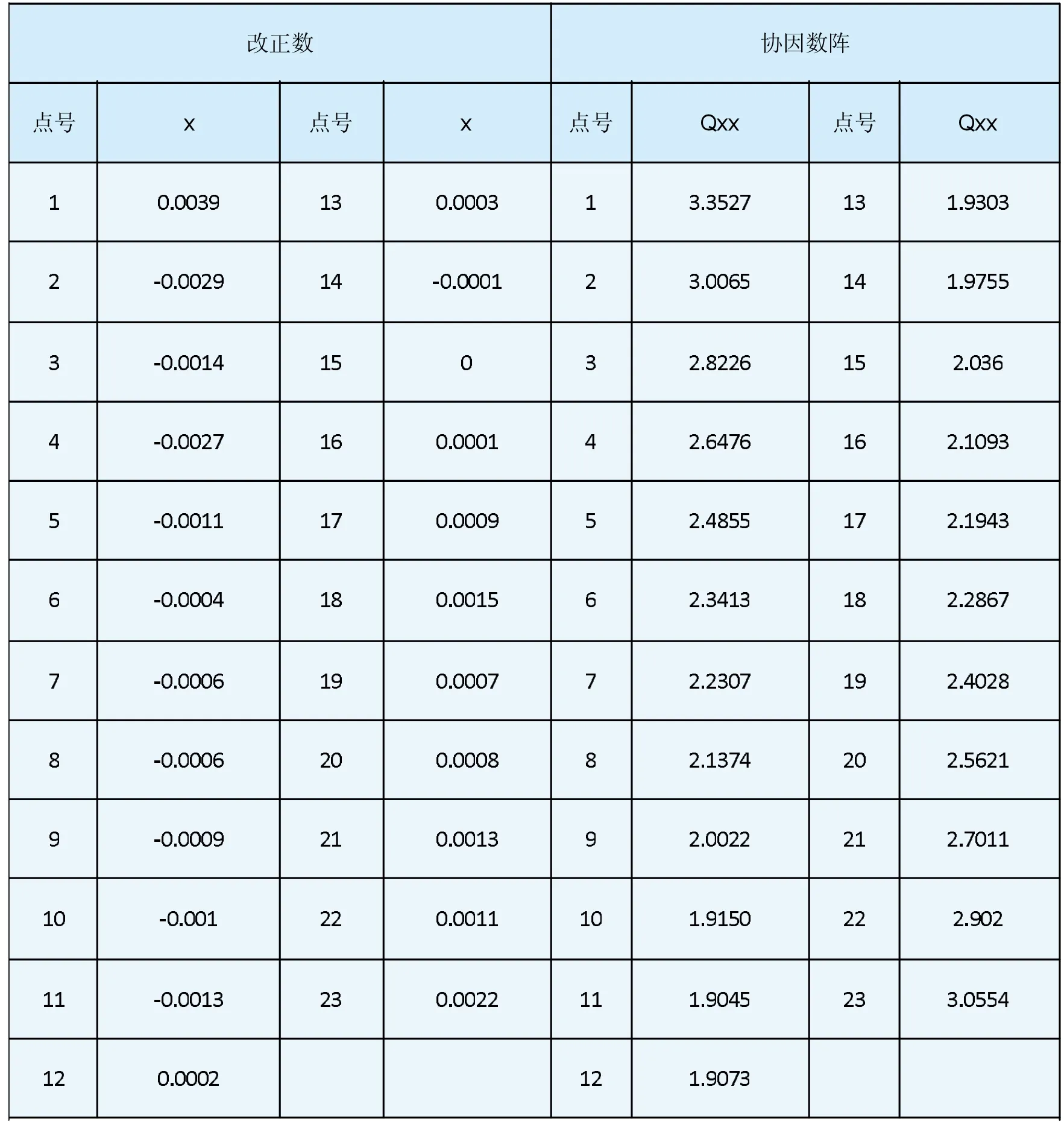
表2 改正數及協因數

對于表2數據，我們將已知點和變形點都當做未知點進行秩虧自由網平差，通過MATLAB得到上表Qxx，由表2Qxx比較可知，10～14點相對于其他點來說，協因數較小，協因數越大權越小，故將其選為穩定點然后進行擬穩平差處理，處理后得到的結果與秩虧自由網處理后得到的結果對比（如表3所示）。

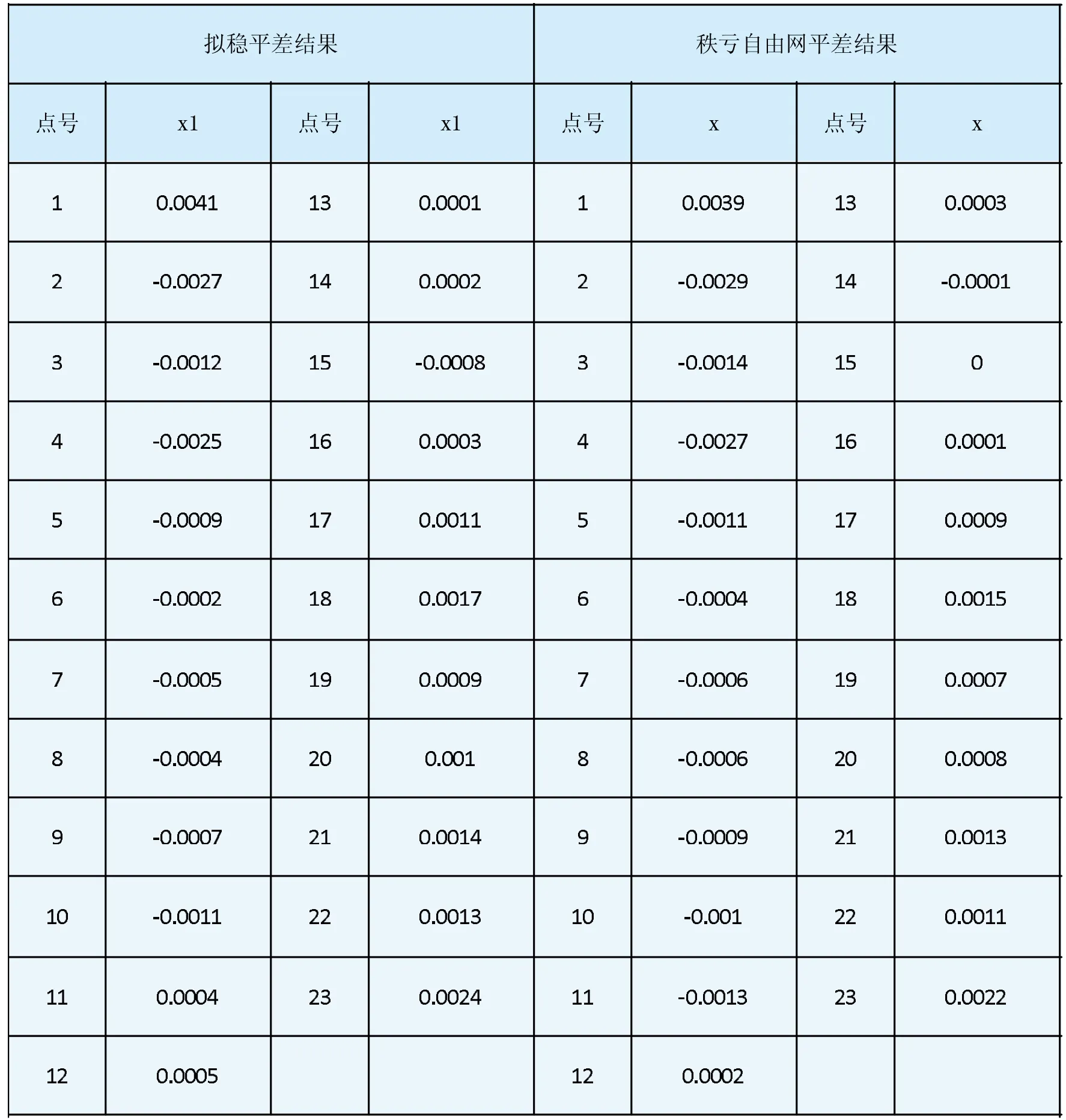
表3 擬穩平差結果與秩虧自由網平差結果對比

2.數據分析

首先收集多個時間段的水準測量值，然后將得到的數據結果進行平差處理，可以得到各個監測點的高程值，以此為基礎，就獲得各個監測點的累積沉降量，再根據建筑物各點的累積沉降量繪制建筑物累積沉降量曲線（如圖1所示），在擬穩平差結果后，將其結果數據作為回歸的變量在對其進行回歸處理，推出回歸方程，達到預測作用，圖 1 為以 1、2、3、4、5 號點為例進行折線圖處理，然后以1號點為例進行預測與實際沉降數據進行對比。

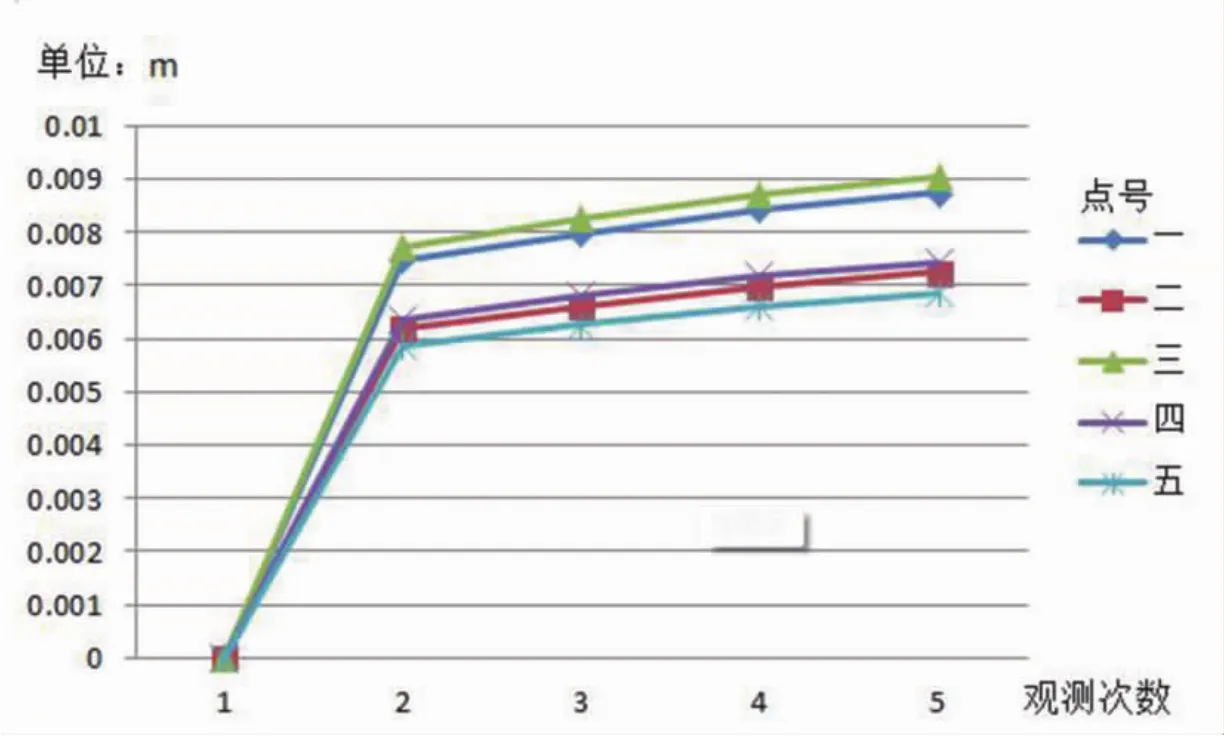
圖1 1-5號點累積沉降量

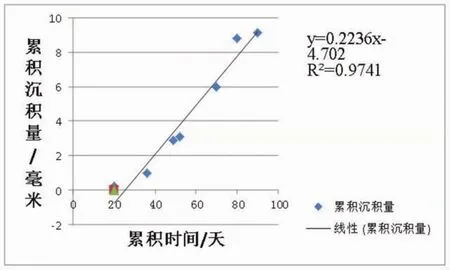
圖2 1號點預測與實際沉降數據對比

可以發現，五個點的累積沉降量相差不大，且沉降速率（折線斜率）大致相同，可見地基處理是相對可靠穩定的。在實際中，沉降的速率是隨時間變化著的，但大體上是趨于直線的，故本次測量是將其看做直線進行處理。沉降折線速率開始動工時，沉降速率很大，隨著建筑工期的增加沉降速率又有所減慢，后面曲線未存在異常離散值，也沒有突然中斷的現象，這些現象說明基礎點和觀測點都是穩定可靠的，不會有很大的沉降，工程在施工階段的下沉平穩，其沉降速率滿足規范要求。

3.數據建模

（1）確定自變量和因變量。因變量為：各監測點前5次累積沉降量。自變量為：建筑物的觀測累積時間；（2）進行回歸分析，設建筑物累積時間為自變量x，累積沉降量為因變量y，假設x和y之間存在著線性關系，利用SPSS軟件建立各點的回歸方程。現以1號點為例來進行說明：將1號點第二次累積沉降量和累積時間數據為因變量和自變量，繪制散點圖，大體呈線性相關，添加線性回歸分析函數，得到圖2和回歸方程，相關系數R2為0.9741，說明高度相關性。

4.結束語

從圖2可以看出，1號點的預測結果與實際觀測值相比較，除了首次相差較大以外，所有觀測時間段的誤差均相對較小。分析原因：預測模型是線性函數關系模型，如果建筑物發生的沉降呈現出完全的線性形態，則預測值將會比較準確。而該點在該時間段的監測數據與前幾期相比較，發生了不均勻的沉降，所以預測值與實測值之間相差較大；最后一次觀測，各監測點的預測結果與實際觀測值相比較誤差均相對較大，是因為大廈荷載增加后，房體整體的沉降量較大。同理，可以對其他點進行以上的分析，分析的結果表明工程的變形量較小，總體是穩定的。

擬穩平差的優越性在于充分考慮了點位變化的情況,使得平差所得的結果更加符合實際情況。本研究首先介紹了擬穩平差的概念、基本原理，討論了擬穩點選取的兩種方法，并舉例說明假設檢測選擇擬穩點法在實際沉降觀測數據處里中的應用。