水文頻率分析的非參數統計計算方法
董 潔,譚秀翠,張慶華,刁艷芳,徐 妍
(山東農業大學水利土木工程學院,山東 泰安 271018)
0 引 言
水利建設規劃設計時,要確定一個合理的設計標準或工程規模。一般采用水文頻率分析方法計算設計值。目前主要有參數和非參數數理統計方法[1]。
用參數法推求設計值xp通常必須解決好兩個基本問題:首先,必須確定水文變量的概率分布模型,即線型選擇;其次,估計所選線型中的未知參數即參數估計[1]。由于水文現象影響因素的復雜性,有些水文學者從統計理論上分析論證水文變量服從的分布,提出了很多線型供選擇,例如P-Ⅲ型分布、對數正態分布和K-M分布等線型,但是水文變量的真實分布是很難確切表達的。在實際水文工作中,常根據實測經驗點據和頻率曲線擬合的好壞選擇線型,由于實際應用中評判擬合優劣的標準各異,所得結論往往相差較大[2]。根據我國水文特點,一般水文變量采用P-Ⅲ型分布。每一種概率分布中都包含若干參數,選定線型后還必須確定其中的參數才能進行頻率計算。但是這些參數是無法根據水文現象的物理機制確定的,必須利用實測資料加以估計。因此,國內外水文學者研究了很多符合水文特點的參數估計方法,主要有適線法,權函數法和概率權重矩法等。由于水文系列長度短,且所需推求的是稀遇的設計值等原因,參數統計估計方法并不理想。
非參數統計中的概率密度估計是指在給定實測樣本后,對其總體概率密度的估計。非參數概率密度估計始于直方圖法,后來發展為最近鄰法、核估計法等,其中理論發展最完善的是概率密度核估計法[3]。
本文把非參數回歸理論應用于水文頻率計算中,建立了水文頻率分析的非參數回歸變換模型,通過變換把樣本變換成“最佳樣本”,“最佳樣本”對應的“最佳函數”具有較高的估計精度。
1 非參數回歸變換理論
設(X1,Y1),…,(Xn,Yn)是R1×1維隨機變量,滿足模型:
Yi=m(Xi)+εi,i=1,2,…,n
(1)
式中:εi是均值為零的獨立隨機變量。
回歸的目的就是根據樣本(Xi,Yi)估計Y關于X的條件概率密度的均值:
m(x)=E(Y|X=x)
(2)
Watston給出了條件均值的核估計:
(3)

由于核回歸是兩個量的比,直接求核回歸的偏差比較困難,可以分別考慮上式分子分母的偏差。
(4)
其中:[m(·)f(·)]″(x)=m″(x)f(x)+2m′(x)f′(x)+m(x)f″(x)。

將原樣本Xi變換為均勻分布的新樣本Ui,目的是對Yi進行加權平均時,權的大小只與樣本的鄰近次序有關,與距離無關,這體現了各樣本互相獨立的原則。只要知道Xi的分布函數F(x),就能進行變換Ui=F(Xi)。
這里假定Xi已經變換成均勻分布的樣本Ui,現在只討論因變量樣本Yi的變換。設Vi是均值為1的隨機樣本,可以進行如下“加法”迭代。
加法迭代的基本原理是將回歸曲線分解成兩條曲線的和,第一條曲線接近回歸曲線,第二條曲線接近常數0。迭代方法如下:
(5)
式中:l是迭代次數。
2 水文頻率分析非參數回歸變換模型的建立
2.1 分布函數的非參數變換估計
分布函數估計與密度估計一樣有許多重要的作用。當樣本數量足夠大時,經驗分布函數可以近似逼近總體的分布函數,但是如果樣本數量較少,表現為階梯函數,使得經驗分布函數估計受到限制。如果想由密度函數估計得到分布函數估計,密度函數估計應是無偏的,方差大點不要緊,因為積分時會消除方差的影響。若要從分布函數得到密度函數估計,分布函數應連續光滑,有點偏差不要緊,數值微分是用鄰近幾個點估計一個點的微分值,對非光滑點(方差大的點)很敏感。因此,一個合理的想法是利用經驗分布的無偏性加以平滑就得到偏差和方差都較小的估計。這種方法是非參數回歸的一個特例,不同之處在于因變量不是事先得到的樣本,而是分布函數的無偏估點計。因此分布函數估計的第一步,是構造無偏估計點作為回歸的因變量。下面采用經驗分布函數作為分布函數的無偏估計。
2.2 樣本經驗分布函數
設x1,x2,…,xn,是隨機樣本,有分布函數F(x),考慮水文的特點,取經驗分布函數是:
(6)
式中:n為樣本的個數;m為樣本x大于等于某個給定值的個數。
對上式的經驗分布函數定義:除x為樣本點外的Fn(x)仍和式(6)一樣,而x=xi處的分布函數估計值為:
(7)
x1≥x2≥…≥xn
其中,α是[0,1]區間的常數,通常取α=1。
由式(6)和式(7)定義的函數稱為樣本經驗分布函數。
提出樣本經驗分布函數的理由如下:先考慮只有一個樣本即n=1,樣本出現對應一次貝努利試驗,出現的概率是α/2,也就是樣本位于α/2分位點。若樣本取自中心較高且具有對稱密度函數的母體,α/2=0.5意味著單個樣本位于分布的中點,對應最大的概率密度。此時的經驗分布函數符合最大似然準則。對于n個樣本,由于各樣本是獨立同分布,樣本分布函數值將分布函數等分。樣本應位于等分后的每小塊中的α/2分位點上,即各樣本等間隔地位于(i-1-α)/(n+1)分位點上。這個想法與離散分布中的古典概率論一致。
顯然,樣本經驗分布函數的性質與經驗分布函數一致,由式(6)知,樣本經驗分布函數是小于等于樣本值的樣本數與樣本總數加一之比,因此nF(xi)是二項分布隨機變量,則有樣本經驗分布函數的均值和方差為:
E[Fn(xi)]=F(xi)
varFn(xi)=F(xi)[1-F(xi)]/n
(8)
所以樣本經驗分布函數是無偏估計,這為回歸提供了好的先決條件。在樣本經驗分布的基礎上回歸,可使分布函數的方差減小。另外,以樣本經驗分布函數為固定點進行內插,也可得到比較光滑連續的曲線,但是這樣得到的曲線保留了樣本經驗分布函數的方差,這個方差的最明顯的證明是對內插得到的曲線進行微分,得到的密度函數估計存在許多毛刺和突起,微分對方差的敏感是檢驗方差存在的直觀方法。
2.3 樣本經驗分布函數的變換回歸
由前面定義知,樣本經驗分布函數是:
(9)
i=1,2,…,n
記yi=Fn(xi) ,則(xi,yi)構成R1×1維隨機變量,可以進行非參數回歸計算。但這里的yi不是通常回歸中事先給出的樣本,是分布函數在xi點的無偏估計。將原樣本(xi,yi)變成新樣本(ui,vi),其中vi是均值為1的隨機變量,ui是均勻分布隨機變量。
由于樣本Xi不是等間隔的固定點,變換回歸包含自變量X和因變量Y的兩步變換,將原樣本(xi,yi)變成新樣本(ui,vi)。在分布函數估計中,這兩步變換可以一起完成,因為Yi和Xi有一定的關系。

(10)
此時的Yi相當于U1,i近似于45°斜線,則:
V1,i=Yi-U1,i+1
(11)


變換回歸的偏差很小,基本上是無偏回歸,因樣本經驗分布函數也是無偏估計,所以最后得到的分布函數估計是無偏估計。
3 蒙特卡羅統計試驗分析
蒙特卡羅統計試驗分析[6,7]可以很好的說明模型的穩健性問題。假設水文變量分別來自P-Ⅲ型分布和對數正態分布總體,用參數統計的適線法和非參數核回歸變換法比較分析模型對總體和樣本數量的穩健性。
3.1 試驗方案
為了考察模型對樣本數量和不同設計頻率的穩健性,分別選取了樣本容量n1=40;n2=50;n3=60;設計頻率p1=0.01,p2=0.001。
3.2 計算方案
用蒙特卡羅方法生成P-Ⅲ型分布和對數正態分布LN樣本,為了考察模型對樣本總體和計算方法的穩健性,設計了108種方案。分別采用非參數的核回歸變換法DRM;參數統計的適線法CFM估計設計值。計算結果見表1和2。(只列出樣本容量為n=60的結果)
3.3 評價指標
(1)均方誤差σ和相對均方誤差δ:

(2)絕對誤差θ和相對誤差?。


3.4 統計試驗結果
統計試驗結果見表1、表2。
3.5 估計方法的比較分析
表1和表2分別用4個評價指標計算了P-Ⅲ型分布和對數正態分布(LN),擬合理論總體是P-Ⅲ型分布和對數正態分布(LN)的穩健性,分析結果如下:
(1)總體是P-Ⅲ型分布。當用P-Ⅲ型分布曲線擬合P-Ⅲ型分布總體時,?xp1≤1%;?xp2≤1%δxp1≤15%δxp2≤20%。
當用對數正態分布(LN)擬合P-Ⅲ型分布,總體適線的穩定性較差,?xp1≥120;?xp2≥20%δxp1≥25%δxp2≥25%。
當用非參數的密度變換法DEM估計設計值,百年一遇和千年一遇的設計值相對誤差一般介于以上兩種情況之間,?xp1≤15%;?xp2≤15%δxp1≤15%δxp2≤20%。
(2)總體是對數正態分布(LN)。當用對數正態分布(LN)擬合對數正態分布總體,?xp1≤8%;?xp2≤8%δxp1≤15%δxp2≤20%。
當用P-Ⅲ型分布擬合對數正態分布LN總體適線的穩定性較差,一般求出的設計值偏小,很不安全。δxp1≥15%δxp2≥20%。

表1 P-Ⅲ型分布理論總體計算成果表(p1=0.01,EX=1 000,p2=0.001)Tab.1 Calculation result of P-Ⅲ theory distribution (p1=0.01, EX=1 000, p2=0.001)
注:各組真值xp如下:Cv=0.5,Cs=1.5時,xp1=2 665,xp2=3 617;Cv=0.5,Cs=2.0時,xp1=2 803,xp2=3 954;Cv=1,Cs=2.5時,xp1=4 875,xp2=7 548。
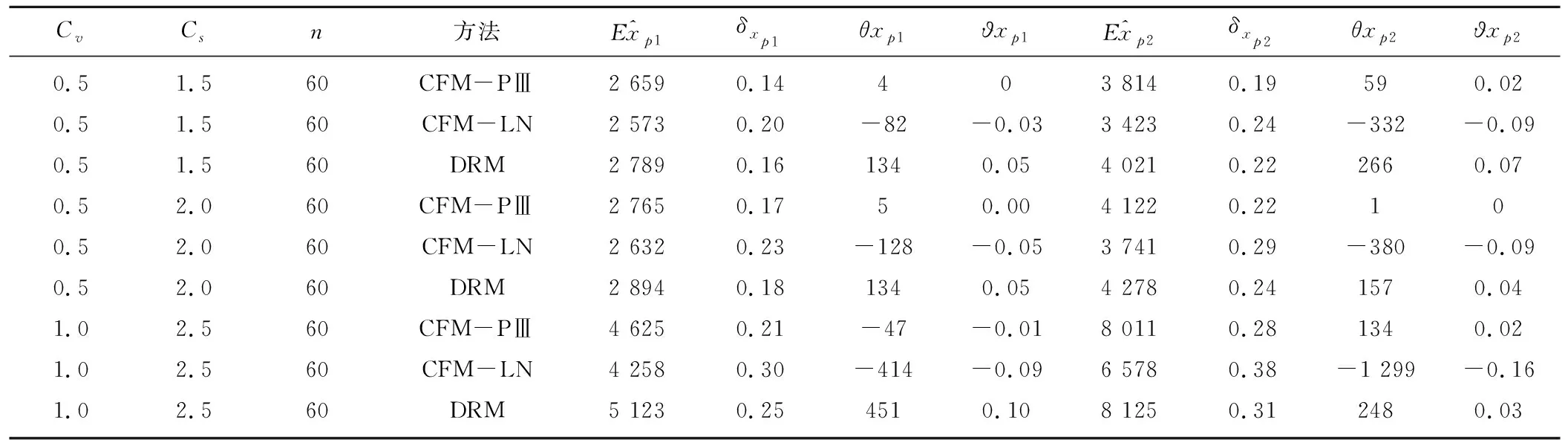
表2 對數正態分布理論總體計算成果表(p1=0.01,EX=1 000,p2=0.001)Tab.2 Calculation result of Logarithmic normal theory distribution (p1=0.01, EX=1 000, p2=0.001)
注:各組真值xp如下:Cv=0.5,Cs=1.5時,xp1=2 665,xp2=3 755;Cv=0.5,Cs=2.0時,xp1=2 760,xp2=4 120;Cv=1,Cs=2.5時,xp1=4 672,xp2=7 877。
非參數的回歸變換法DEM估計設計值,百年一遇和千年一遇的設計值相對誤差一般介于以上兩種情況之間,?xp1≤15%;?xp2≤15%δxp1≤15%δxp2≤20%。
當樣本容量由40、50增加到60,相對誤差和相對均方誤差減小,說明樣本容量增加,穩定性增加。
4 應用實例研究
為了更好地檢驗該模型的適用性,以下對具有代表性的小浪底站77 a;宜昌站132 a;崗南站57 a;平山站30 a和黃壁莊站56 a的年最大洪峰流量系列,用P-Ⅲ適線法和變換回歸模型進行了頻率分析計算,各站年最大洪峰流量系列資料表詳見文獻[8],計算成果見表3。通過以上計算可以看出,用非參數回歸變換模型計算出的設計值比適線法計算的值普遍偏大,頻率P大于百年以上的設計值較參數適線法計算的設計值大3%~7%;頻率P小于百年以下的設計值較參數適線法計算的設計值大2%~3%。

表3 小浪底站、平山等站年最大洪峰流量頻率分析結果Tab.3 Flood frequency analysis of the XIAOLANGDI station and PINGSHAN station
5 結 語
(1)我國水文頻率計算一般采用參數統計的“適線法”。需要事先假定水文變量服從某種線型分布,如果假設線型和實際分布不符就會影響計算結果。非參數統計方法不需要假定線型,但是理論上要求適用于大樣本。本文建立的非參數回歸變換方法通過對小樣本進行變換,不僅拓展了非參數統計的應用,還提高了小樣本的估計精度。
(2)用蒙特卡羅統計試驗方法考察模型的穩健性問題。通過對水文計算中常用的P-Ⅲ型和對數正態分布兩個總體,用參數統計的“適線法”和非參數統計的“變換回歸”兩種估計方法比較分析了三組參數、三組樣本。結果表明,模型是穩健的,方法是合理的。
(3)以我國幾個有代表性的測站的年最大洪峰流量為例,比較研究變換回歸模型和參數適線法在水文頻率分析計算中的結果特征,通過計算得到用非參數方法計算的水文頻率結果較適線法偏大,多種計算結果可以互相參考,為水利工程規劃提供了一種有效方法。

