氣介式自校正聲波水位計精度研究

鄭貴林，董啟鵬

(武漢大學動力與機械學院自動化系，武漢 430072)

0 引 言

在電子技術被引入水位計的研制之前，水位計大多是通過測量與水相關的參數來間接轉化為水位參數，以達到水位測量的目的，如浮子式和壓阻式水位計[1]。后來，隨著傳感器技術和嵌入式技術的發展，出現了更多的水位測量方法，比如利用雷達、激光、超聲波等技術的水位測量傳感器，具有智能控制功能，可實現非接觸式測量，且精度高、穩定性好[2]。

牛睿平等在文獻[3]中提出了一種新型國產雷達水位計的設計，蓋志剛等在文獻[4]中提出了一種新型激光智能水位測量系統的研制，藍標在文獻[5]中提出了高精度氣介式超聲波水位計的設計，湯祥林等在文獻[6]中提到的低功耗、高精度超聲波水位計的研制。

以上文獻中研究的新型水位計，量程都相對較小，對環境要求較高。而對于庫容較小的水庫而言，采用雷達水位計和激光水位計成本較高，采用超聲波水位計受環境影響較大。因此，設計一種量程相對較大，成本較低，對環境敏感度不高，且易于安裝的水位計，可以很好地解決以上問題。針對此需求，本文設計了一種氣介式自標定聲波水位計，創新地采用了AD采集與sinc內插算法相結合的峰值檢測方法，避免了傳統的由于采用閾值比較法而對回波進行復雜硬件電路的處理，并進行了長期實驗。

1 聲波水位計原理

本文設計的氣介式自標定聲波水位計采用空氣聲學回聲測距原理，借鑒的是超聲波測距中最常用的脈沖回波法，結合可聞聲波換能器的聲學特性，最終設計出了該傳感器測量系統。

該系統測量原理即是控制聲波換能器即揚聲器發射聲波信號，聲波在空氣中傳播時，遇到不同體積或材質的物體，將會有不同形式、不同幅值的回波[7]。由于揚聲器不同于超聲波換能器能在脈沖的激勵下，產生單一頻率的超聲波信號，揚聲器在輸入脈沖信號時，只會產生其頻率響應范圍內的信號，所以本設計中輸入信號采用單一頻率的正弦信號。為了避免環境中溫度、濕度、大氣壓等環境因素的影響，本設計中采用聲學自校正的方法。

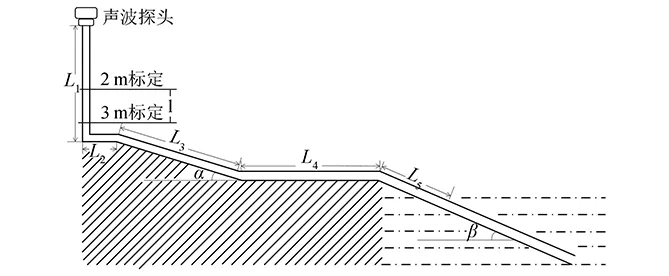
圖1 測量示意圖Fig.1 Instrumentation plan

該水位計主要由聲波探頭、波導管及測控單元組成，測量示意圖見圖1。圖1中L1表示的是聲波探頭安裝位置至第一拐點的長度，L2、L3和L4為按現場大壩鋪設的長度，L5為最后一個拐點至水面的長度，α和β為鋪在斜坡上的波導管的角度。l為兩個標定點的距離，L為從聲波探頭至測量水面的總長度。

聲波在空氣中的傳播速度為v，如果測得聲波從開始發射到接收到反射回波的時間t，就能計算出從聲波探頭到反射面的距離S，即：

S=vt/2

(1)

測量時，由聲波探頭發射的聲波信號沿波導管到達水界面產生反射回波，然后返回至聲波探頭而被接收，所以只需準確測出聲波信號從開始發射到接收到回波信號的時間t1及傳播的聲速c1，便可計算出聲波探頭反射面至水面的距離。即：

L=c1t1/2

(2)

聲波在波導管中傳播速度的影響因素有溫度、濕度、大氣壓等，所以要想利用式(2)準確測得聲波探頭反射面距水面的距離，那么就要解決上述影響因素的干擾，因此在本設計中采用了自校正技術對聲速進行補償。其方法是在距聲波探頭2 m處和3 m處分別放置一塊擋板，如圖1中2 m和3 m標定處，聲波在標定處會產生回波，由于2 m到3 m的距離是已知的，所以這段時間可以作為聲波此時在管道中傳播1 m的基準值，記這個時間基準值為t2，此時，如果聲波傳播的聲速為c2，即有：

l=c2t2/2

(3)

將聲波在這段時間基準值內傳播的距離與聲波傳播到水面反射面的距離做比則有：

(4)

由上式可知，聲程L是傳播速度c1、c2與傳播時間t1、t2和時間基準值內傳播距離l的函數。若近似認為在波導管中不存在溫度梯度時，那么可得c1=c2，則式(4)可化簡為：

(5)

故在忽略波導管內溫度梯度的情況下，只需測出t1、t2，即可測出聲波探頭到水面的距離。

計算出聲波探頭至水面距離后，根據L1、L2、L3、L4和L5來判斷水位處于哪一段波導管中。假設聲波探頭安裝位置高程為H1，測出聲波探頭至水面距離L，且判斷出水面在L5段，那么水位H可由下面公式得出：

H=H1-L1-L3sinα-(L-L1-L2-L3-L4) sinβ

(6)

若判斷出水位處于L3段，那么水位H由下面公式得出：

H=H1-L1-(L-L1-L2) sinα

(7)

2 系統設計與實現

系統具體實現如下：由ST公司基于ARM Cortex-M3內核的STM32F103微控制器控制信號產生電路產生單一頻率的正弦波信號，經發射信號處理電路處理后，由信號功放電路放大送入揚聲器驅動發聲。由麥克接收回波信號，并進行阻抗匹配，然后經過Maxim公司的麥克專用放大器進行前置放大，這時的信號還不滿足信號處理的要求，所以還要進行信號調理，最終經過信號調理后的波形由STM32進行AD采集，并采用sinc內插算法高度還原波形，以更精確地得出實時水位。實時波形及相關數據通過RS485總線或GPRS模塊上傳至云端服務器，并通過上位機顯示和查看。系統實現框圖如圖2所示。

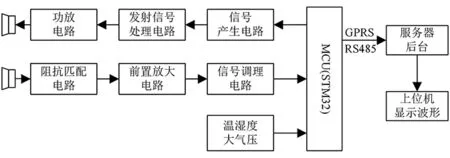
圖2 系統實現框圖Fig.2 System structure

該聲波探頭實物如圖3所示，安裝時開口處朝下接波導管，上端封閉，引出電源線與太陽能板相連。

圖3 聲波探頭實物 Fig.3 Sonic probe

3 精度影響因素

在本設計中，主要有三個因素會對測量精度造成影響，分別是聲源的選擇、功放電路與揚聲器是否匹配及回波時間捕捉的精確性。

3.1 聲源的影響

由于可聞聲波采用揚聲器作為換能器，在激勵信號即聲源的使用上不同于超聲波換能器，超聲波換能器在脈沖激勵信號的驅動下，可發射其固有頻率的超聲波。但揚聲器的頻響范圍比較有限，當輸入方波信號時，揚聲器并不能復現方波信號[8]。基于此，在本研究中，將聲源信號確定為單一頻率的正弦信號，頻率在1～20 kHz，正弦波產生方式采用直接數字頻率合成技術(DDS)，使用ADI公司的可編程波形發生器AD9833。

3.2 功放電路與揚聲器匹配的影響

揚聲器是瞬態表現的最大瓶頸，要求瞬態表現好，則揚聲器振膜需要做到快速到位的運動，這對揚聲器的控制力提出了非常苛刻的要求[9]。而要響應高于2 kHz頻率的輸入信號，需要用高頻喇叭繼續試驗。

另外，“瞬態表現好”需要大功率功放和電源支持的，信號迅速提升的瞬間，峰值功率可能會是平均功率的數倍甚至十余倍，基于這個原因，選取了2 W的高頻喇叭實驗，并更換功率10 W的功放，以使揚聲器可以瞬間響應輸入頻率。

3.3 捕捉回波時間準確性的影響

傳統的回波信號檢測方法有幅值檢測法、相位檢測法和渡越時間法，而采用最多的渡越時間法。渡越時間法又包括閾值檢測法、峰值時間檢測法[10]等。本設計中采用峰值時間檢測法，但不采用傳統的硬件方法，而是將接收到的聲波信號的模擬量通過STM32內置AD轉換成數字量，利用sinc內插算法對采樣點重構波形，從而更精確地得到峰值點，就可以計算出回波時刻。

信號插值是增加抽樣率以增加數據的過程，一般的信號插值基本結構[11]如圖4所示。

圖4 信號插值基本結構Fig.4 The structure of Signal interpolation

假設采樣序列為x(n),原采樣率f，在x(n)的每兩個采樣點之間等間隔插入(L-1)個零點,得到一個新的采樣序列v(n),即：

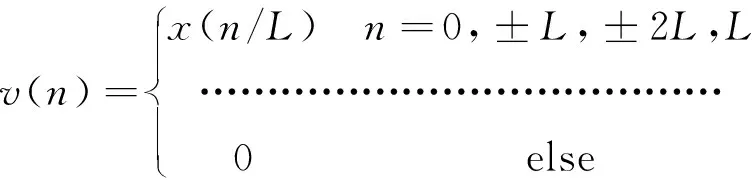
插零后信號的頻譜：

于是可得：

V(ejw)=X(ejwL)

即插零后信號頻譜V(jw)(-π/L～π/L) 內等于X(ejw)，相當于將X(ejw)作了周期壓縮。 然后再通過一個低通濾波器：

就可以將高頻信號濾掉從而得到插值后的信號y(n)。信號插值過程示意圖如圖5所示，圖5(a)為原信號x(n)及其頻譜X(ejw)，圖5(b)為插入零值點后的信號v(n)及其頻譜V(ejw),圖5(c)為插值后信號y(n)及其頻譜Y(ejw)：

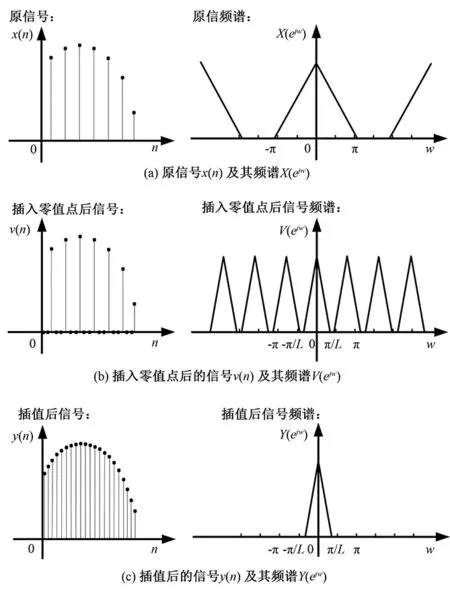
圖5 信號插值過程Fig.5 The process of signal interpolation

由參考文獻[12]，利用sinc函數內插的公式為：

(8)

式中Δ=1/f。

4 實驗分析

基于上述影響因素搭建了實驗，聲源信號采用5 kHz單一正弦波，揚聲器功率2 W，采用駐極體話筒來接收回波，并進行信號調理。經STM32的AD采樣后，將采樣數據發送到上位機進行顯示。從開始發送聲波到接收回波時間內采集的離散點如圖6所示，橫坐標為采樣周期，縱坐標為AD采集值，AD為12位 1 MHz采樣率。圖中相鄰離散點通過線段相連從而繪制出整體波形。由于AD采集只能采集到正值，所以波形只有正弦正半波。圖6中，第一個正弦半波為2 m處回波，第二個正弦半波為3 m處回波，幅值最高處為目標處回波。

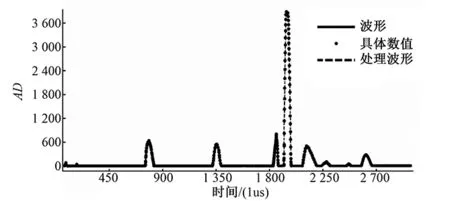
圖6 AD采集波形Fig.6 AD waveform acquisition

將最高處正弦半波放大，經多次實驗觀察放大后的波形，采集的最高點并不是峰值點，要想精確地捕捉到三個正弦半波的峰值點，就要用sinc插值公式(8)來對波形進行處理。放大后的原峰值附近波形及利用sinc插值算法得出的波形如圖7所示，橫坐標為時間t，縱坐標為AD采集值。這里只把原波形的包括最高點在內的16個點畫出，其中最高點附近6個點的坐標分別為：

(6,3 836)(7,3 926)(8,3 985)(9,3 972)(10,3 912)(11,3 813)

在每兩個采樣點之間插入了4個零值，即采樣率提高了5倍，插值后的波形最高點附近6個點的坐標分別為：

(7.8,3 969)(8,3 985)(8.2,3 987)(8.4,3 990)

(8.6,3 986)(8.8,3 980)

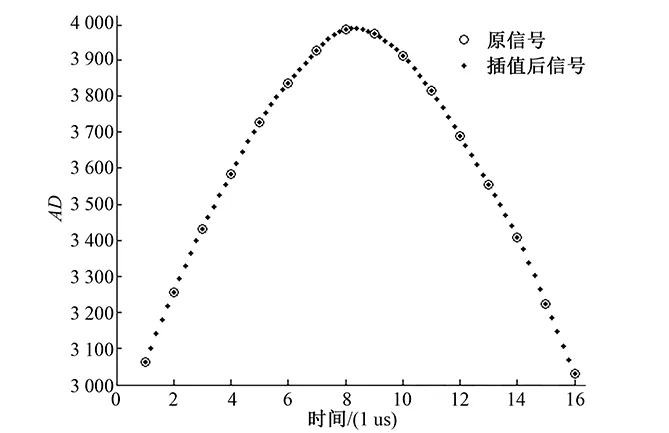
圖7 原波形與正弦插值后波形 Fig.7 The waveform of before and after processing

于是可以根據插值后新的序列來比較出最高點作為新的峰值點，同樣的，對2 m和3 m處回波作sinc插值處理。然后利用公式(5)計算聲程，再用公式(6)或(7)計算出水位。相比于根據原波形計算出的峰值時刻點，在進行聲波測水位實驗時，實測結果與測量結果的偏差較小。表1實驗數據為部分實驗水位、實測水位及誤差，表中實驗水位1為根據原波形計算出的實驗水位，誤差1為實驗水位1與實際水位相比較的誤差，實驗水位2為根據正弦插值算法處理后的波形計算出的實驗水位，誤差2為實驗水位2與實際水位相比較的誤差。

表1數據表明隨著實際水位的增高，利用原波形的AD采樣數據進行計算的水位結果與實際水位的偏差會稍微變大，但是利用經過正弦插值算法處理的波形，進行計算，可以保證誤差在1 cm之內。

此外，在實驗室搭建了模擬環境，改變該水位計所處環境溫度和環境濕度，檢測溫濕度對于測量精度的影響。實驗結果分別如表2、表3所示。

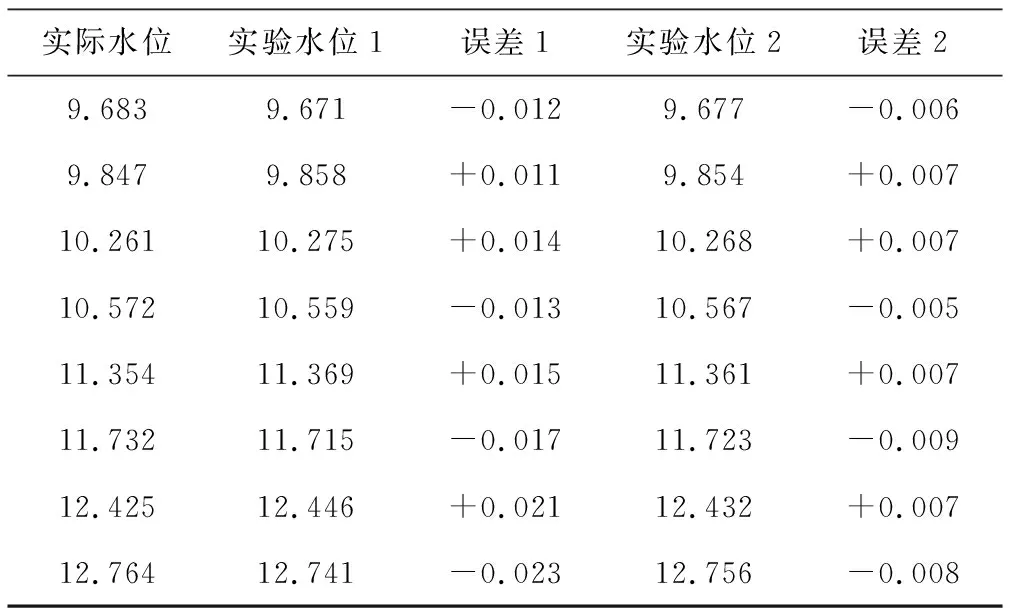
表1 實驗結果對比 m

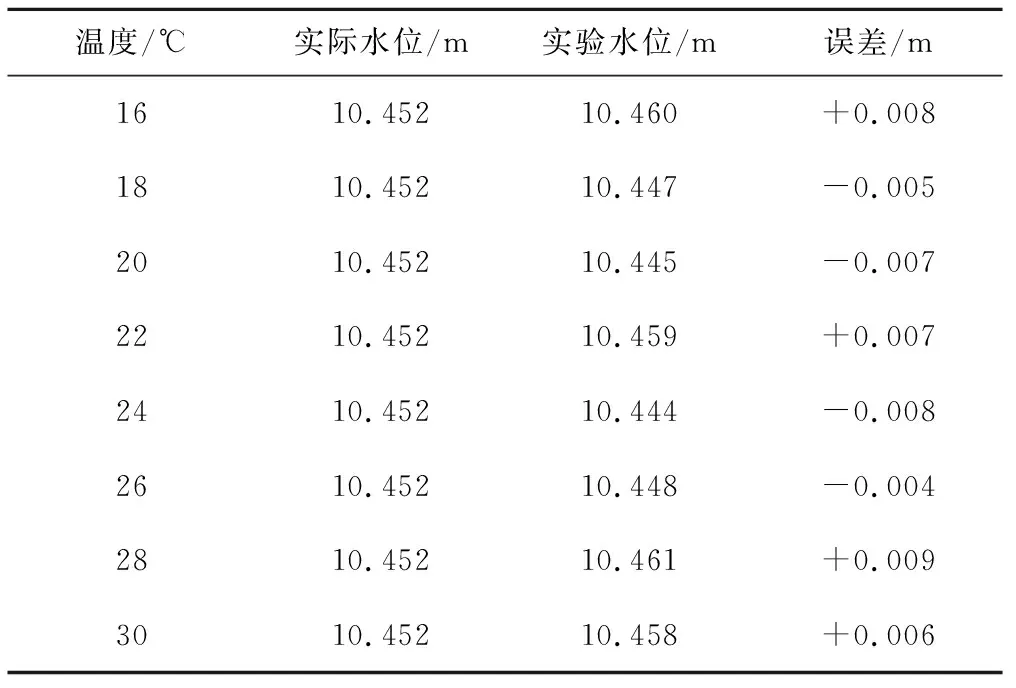
表2 溫度變化實驗數據Tab.2 Experimental data on temperature change

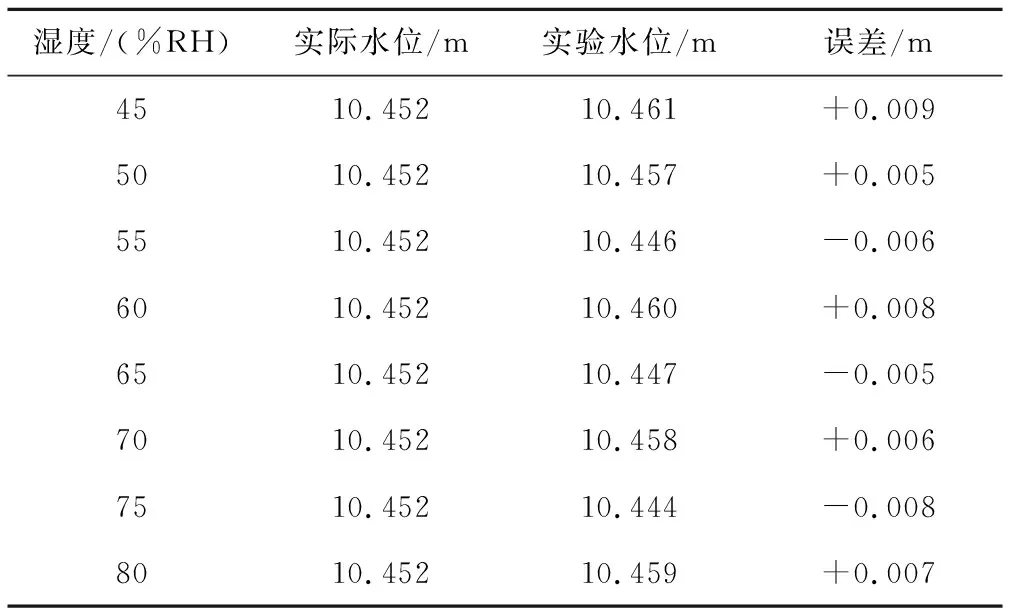
表3 濕度變化實驗數據Tab.3 Experimental data on humidity change

表2和表3的實驗數據表明在1 cm誤差范圍之內，測量精度不受環境溫度和濕度的影響。

除溫濕度外，由于氣介式聲波水位計常用于野外水位監測，所以傳統的測量方式會受到風、波浪的影響，但在本設計中，可聞聲波的傳播是在相對封閉的波導管中，聲波的傳播不會受風向或波浪的影響。為了說明此情況，取安裝于荊門某小型水庫的該氣介式聲波水位計的實測數據進行分析，兩天均無降雨，風力分別為1級和3級。具體數據如表4所示，在9∶00-12∶30時間段內，每0.5 h采集一次水位，中間一欄為風力為1級時的實測水位，右邊一欄為風力為3級時的實測水位。

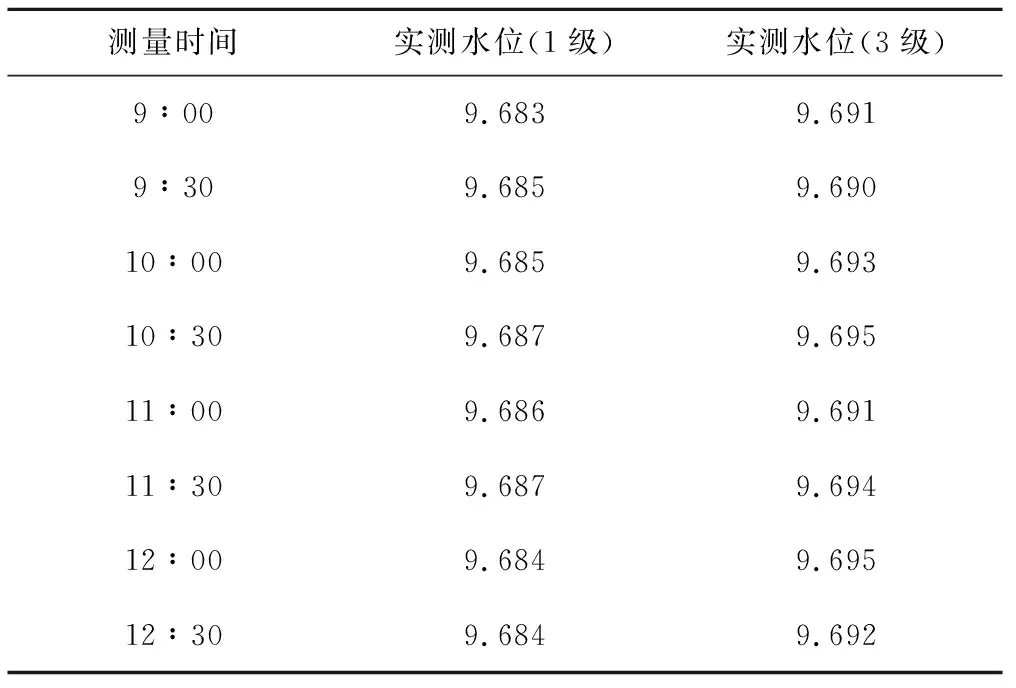
表4 風力實驗結果對比Tab.4 Comparison of wind test results

5 結 語

本文闡述了一種氣介式自校正聲波水位計，該水位計采用對波形進行AD采集與sinc內插相結合的軟件處理方法，使得系統在20 m測量范圍內的絕對精度可以達到1 cm。且根據此前安裝在荊門市某小型水庫的水位計運行情況來看，測量結果基本不受環境溫濕度變化及風力的影響，測量可靠性較高，實時水位、溫濕度等信息可以上傳至服務器，在實際運行中能夠滿足此類小型水庫“低成本，穩定可靠，安裝簡便”的需求。