基樁正常使用極限狀態失效概率區間估計方法

桑 意 平

(1. 武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072；2. 武漢大學 水工巖石力學教育部重點實驗室，武漢 430072)

0 引 言

基樁是巖土工程中常見的巖土結構物。在基樁正常使用極限狀態失效概率估計中，表征荷載-位移關系的雙曲線參數通常被視為關鍵的隨機變量[1-7]。此外，現有研究[5-7]表明基樁荷載-位移雙曲線參數具有明顯的負相關性，且這種負相關性對基樁失效概率的估計具有顯著的影響，忽略雙曲線參數的負相關性將嚴重高估基樁的失效概率。為了更加準確地估計基樁失效概率，實際工程應該充分考慮雙曲線參數的負相關性，建立雙曲線參數的二維分布模型。近年來，Copula方法[8]為基樁荷載-位移雙曲線參數二維分布模型的建立提供了一條簡單而有效的途徑[5-7]。Copula方法相比其他方法的優勢是，它將二維分布模型的構造簡化為邊緣分布函數的估計與Copula函數的選擇問題，且邊緣分布函數估計與Copula函數選擇分開獨立進行[5-7]。

試驗數據是Copula方法構造二維分布模型的基礎。當試驗數據的樣本數目無窮大時，基于試驗數據建立的二維分布模型是精確的。然而，受技術經濟條件的限制，實際工程中試驗數據非常有限，基于有限試驗數據建立的二維分布模型不可避免地存在較大的統計不確定性，這是因為基于有限試驗數據估計的統計量如樣本均值、標準差、相關系數和AIC值具有明顯的變異性[9,10]。傳統的基樁失效概率估計方法幾乎無一例外地忽略了雙曲線參數的統計不確定性，這些方法只能得到基樁失效概率的點估計。該點估計僅考慮了雙曲線參數本身固有的變異性，而沒有考慮因試驗數據有限引起的統計不確定性。由于統計不確定性的存在，失效概率的點估計可能無法真實反映基樁的安全度。根據統計學理論，當考慮雙曲線參數的統計不確定性時，基樁失效概率本質上是一個概率分布，此時將基樁失效概率表示為具有一定置信度水平的置信區間即失效概率的區間估計是一種更加合理的方法[11-13]。

實現基樁失效概率區間估計的關鍵一步是表征雙曲線參數二維分布模型的統計不確定性。該統計不確定性可以通過直接模擬雙曲線參數試驗數據的統計量如樣本均值、標準差、相關系數和AIC值的變異性來表征。然而，常規方法模擬統計量變異性需要已知大量與試驗數據相同樣本數目的樣本，這在工程上是不可能實現的。幸運的是，作為重抽樣方法的Bootstrap方法[14]為統計量變異性的直接模擬提供了一種有效的工具。Bootstrap方法通過對原始試驗數據進行有放回地隨機抽樣獲得大量的與原始試驗數據相同樣本數目的Bootstrap子樣本，基于Bootstrap子樣本即可計算統計量的估計值并獲得統計量的變異性。Bootstrap方法模擬統計量變異性只需已知原始試驗數據，無需對統計量的實際分布作任何假設和增加新的數據觀測。Bootstrap方法的上述優點使得它在巖土工程領域巖土體參數統計量變異性模擬方面獲得了廣泛的應用[10-13]。

本文目的在于提出基樁正常使用極限狀態失效概率區間估計方法，推動基樁失效概率估計從傳統的點估計向區間估計轉變。為此，首先介紹了基樁標準化荷載-位移雙曲線參數的定義，并給出了鉆孔現澆灌注樁(ACIP)雙曲線參數的現場試驗數據。其次，基于試驗數據采用Copula方法構造了雙曲線參數的二維分布模型，并應用Bootstrap方法表征了雙曲線參數二維分布模型的統計不確定性。最后，給出了考慮雙曲線參數二維分布模型統計不確定性的基樁失效概率區間估計方法，并比較了基樁失效概率點估計和區間估計結果的優缺點。

1 基樁標準化荷載-位移雙曲線模型

1.1 雙曲線參數的定義

基樁的荷載-位移關系是基樁設計的基礎。為了得到基樁的荷載-位移關系，首先需要開展荷載試驗獲取荷載-位移數據，然后采用一定的模型如雙曲線模型、冪函數模型、指數函數模型、GM(1, 1)模型等擬合荷載-位移數據，從而得出基樁的荷載-位移關系曲線。由于參數較少且物理意義明確，雙曲線模型在擬合基樁的荷載-位移關系曲線中應用最為廣泛。為了進一步減小實測基樁荷載-位移雙曲線的離散性，有學者[4-5]提出采用基樁的實測極限承載力對基樁荷載-位移雙曲線模型進行標準化，該標準化的基樁荷載-位移雙曲線模型如下式所示：

(1)

式中：Q為基樁軸向荷載；QSTC為基樁的實測極限承載力；y為樁端位移；a和b是雙曲線模型中兩個參數，它們均具有明確的物理意義(見圖1)，其中a為雙曲線初始斜率的倒數，而b為雙曲線極限值的倒數。可見，基樁標準化荷載-位移雙曲線模型由雙曲線參數a和b唯一確定。

圖1 雙曲線參數的定義Fig.1 Definition of hyperbolic curve-fitting parameters

1.2 雙曲線參數現場試驗數據

如前所述，雙曲線參數a和b是基樁正常使用極限狀態失效概率估計的關鍵變量。為此，以文獻[6]中鉆孔現澆灌注樁(ACIP)雙曲線參數現場試驗數據(樣本數目N=40，屬于非常有限的試驗數據)為例建立a和b的二維分布模型，并估計基樁的正常使用極限狀態失效概率。圖2給出了雙曲線參數試驗數據的散點圖及其生成的40條基樁荷載-位移雙曲線。由于場地變異性和基樁制造缺陷的存在，同一場地的同類型基樁得到的荷載-位移關系曲線并不相同，而是表現出明顯的離散性，與之對應的荷載-位移雙曲線參數a和b展現出顯著的變異性。此外，a和b還具有明顯的負相關性，由試驗數據計算知：a和b的Kendall秩相關系數τ為-0.548。下面采用Copula方法建立a和b的二維分布模型以表征a和b的變異性和負相關性。

圖2 雙曲線參數試驗數據及基樁標準化荷載-位移雙曲線Fig.2 Test data for a and b and the resulting normalized hyperbolic load-displacement curves for single piles

2 基于Copula方法的雙曲線參數二維分布模型構造

2.1 Copula方法

本文采用Copula方法構造雙曲線參數a和b的二維分布模型。根據Sklar定理[8]，a和b的聯合分布函數F(a,b) 和聯合概率密度函數f(a,b)可以分別表示為：

F(a,b)=C[F1(a),F2(b);θ]=C(u1,u2;θ)

(2)

f(a,b)=f1(a)f2(b)D[F1(a),F2(b);θ]=

f1(a)f2(b)D(u1,u2;θ)

(3)

式中：C(u1,u2;θ)為二維Copula函數；D(u1,u2;θ)為二維Copula函數的密度函數；θ為Copula函數的相關參數；u1=F1(a)和u2=F2(b)分別為a和b的邊緣分布函數；f1(a)和f2(b)分別為a和b的概率密度函數。因此，若已知a和b的邊緣分布函數和Copula函數，利用式(2)和式(3)就可以構造出a和b的聯合分布函數和聯合概率密度函數。

2.2 雙曲線參數二維分布模型

Copula方法構造雙曲線參數a和b的二維分布模型包括以下獨立的兩步：①確定a和b的邊緣分布函數；②選擇最優的Copula函數表征a和b的相關結構。基于圖2所示的試驗數據，下面采用Copula方法構造a和b的二維分布模型。

首先確定a和b的邊緣分布函數。為此，選取巖土工程中常用的正態分布、對數正態分布、極值I型分布和威布爾分布作為備選邊緣分布函數擬合a和b的邊緣分布。為了避免出現負值，正態分布和極值I型分布在0處進行左截尾。上述4種邊緣分布函數的分布參數可以利用a和b的均值和標準差求出(a的均值和標準差分別為5.15和3.07 mm；b的均值和標準差分別為0.62和0.16)。

在確定了備選邊緣分布函數的分布參數之后，下一步就是采用AIC準則[15]識別出擬合試驗數據最優的邊緣分布函數。一般來說，具有最小AIC值的邊緣分布函數被認為是擬合試驗數據最優的邊緣分布函數。對于參數a來說，基于試驗數據計算的正態、對數正態、極值I型和威布爾分布的AIC值分別為202.47、196.03、194.71和196.53，最優的邊緣分布是極值I型分布；對于參數b而言，4種分布的AIC值分別為-29.12、-30.32、-28.26和-27.53，最優的邊緣分布是對數正態分布。

其次選擇最優的Copula函數表征a和b的相關結構。眾所周知，數學上存在多種二維Copula函數可以用來擬合隨機變量的相關結構，如Gaussian、Plackett、Frank、Clayton、Gumbel、FGM、AMH Copula等。鑒于a和b具有明顯的負相關性，選取巖土工程中常用的Gaussian、Plackett、Frank和No.16 Copula函數[8]作為備選Copula函數擬合a和b的相關結構。上述4種Copula函數都能表征a和b的負相關性，且相關系數絕對值都能達到1，非常適合表征a和b的相關結構[8]。這些Copula函數的相關參數θ可以利用a和b的Kendall秩相關系數τ求出(Kendall秩相關系數τ為-0.548)。

在確定了備選Copula函數的相關參數θ之后，下一步就是采用AIC準則[15]識別出擬合試驗數據最優的Copula函數。同理，具有最小AIC值的Copula函數被認為是擬合試驗數據相關結構最優的Copula函數。為此，計算了Gaussian、Plackett、Frank和No.16 Copula函數的AIC值，它們分別為-27.01、-31.37、-27.52和-28.25，可見Plackett Copula函數是擬合鉆孔現澆灌注樁(ACIP)的雙曲線參數相關結構最優的Copula函數。

3 基于Bootstrap方法的雙曲線參數統計不確定性表征

3.1 Bootstrap方法

如前所述，基于有限試驗數據估計的統計量如樣本均值、標準差、相關系數和AIC值具有較大的變異性，這種變異性導致基于有限試驗數據建立的二維分布模型存在明顯的統計不確定性。為了表征a和b的二維分布模型的統計不確定性，本文采用Bootstrap方法模擬雙曲線參數試驗數據的統計量變異性。Bootstrap方法由Efron于1979年提出，它的基本原理是：通過對原始試驗數據進行有放回地隨機抽樣獲得大量與原始試驗數據相同樣本數目的Bootstrap子樣本，然后基于Bootstrap子樣本計算統計量的估計值，最終獲得統計量的變異系數及其概率分布。Bootstrap方法只需已知原始試驗數據，無需對統計量的實際分布作任何假設以及增加新的數據觀測。盡管簡單，但是該方法的理論依據及其良好的收斂性早已被統計學家所證明[14]。

令雙曲線參數的試驗數據為X={(ai,bi),i= 1, 2,…,N}，從中有放回地隨機抽樣N次，每次抽取雙曲線參數的一次觀測，從而得到一個與X相同樣本數目的Bootstrap子樣本Bj={B1,j,B2,j, …,BN,j}，該抽樣過程如圖3所示。由于是有放回地隨機抽樣，因此在Bj中雙曲線參數的某次觀測(ai,bi)可能出現一次、多次或零次。重復上述步驟Ns次，即可獲得Ns個Bootstrap子樣本。一般來說，為了達到良好的收斂效果，Bootstrap子樣本數目Ns通常取值較大。參考前人的研究結果[10-13]，本文采用Ns=104模擬統計量如樣本均值、標準差、相關系數和AIC值的變異性。Ns個Bootstrap子樣本可以得到Ns組樣本均值、標準差、相關系數和AIC值。根據這些數值即可獲得樣本均值、標準差、相關系數和AIC值的概率分布和變異系數。

圖3 Bootstrap方法抽樣示意圖Fig.3 The generation of one bootstrap sample

3.2 雙曲線參數統計不確定性

由于Copula方法構造的二維分布模型由邊緣分布函數和Copula函數組成，因此研究雙曲線參數二維分布模型的統計不確定性可以轉化為研究邊緣分布函數和Copula函數的統計不確定性。

首先研究邊緣分布函數的統計不確定性。圖4給出了Bootstrap方法模擬的a和b樣本均值和樣本標準差的概率密度函數。可以看出，基于有限數據估計的樣本均值和標準差具有較大的變異性，如a的樣本均值和標準差的變異系數分別為0.09和0.17，b的樣本均值和標準差的變異系數分別為0.04和0.12，可見高階矩的樣本標準差比低階矩的樣本均值變異性更大，表明樣本標準差比樣本均值更加難以準確估計。樣本均值和標準差的變異性將導致a和b的邊緣分布函數的分布參數具有統計不確定性，這是因為邊緣分布函數的分布參數是根據樣本均值和標準差確定的。

圖4 樣本均值和標準差的概率密度函數Fig.4 Probability density functions of sample mean and standard deviation for a and b

圖5給出了Bootstrap方法模擬的4種備選邊緣分布函數AIC值的概率密度函數。可以看出，基于有限數據估計的AIC值也具有較大的變異性。對于參數a來說，正態、對數正態、極值I型和威布爾分布的AIC值變異系數分別為0.06、0.06、0.06和0.06；對于參數b而言，4種分布AIC值變異系數分別為0.30、0.27、0.29和0.31。4種備選邊緣分布函數AIC值的變異性將導致a和b的邊緣分布函數的分布類型具有統計不確定性，這是因為邊緣分布函數的分布類型是根據AIC值識別的。此外，4種備選邊緣分布函數AIC值的概率密度函數重疊區域較大，這進一步說明4種備選邊緣分布都有可能被識別為最優邊緣分布函數。下面分析a和b的邊緣分布函數的分布類型不確定性。

圖5 4種備選邊緣分布函數AIC值的概率密度函數Fig.5 Probability density functions of AIC scores for the four candidate marginal distributions

基于每個Bootstrap子樣本計算的4種備選邊緣分布函數的AIC值即可識別出該子樣本的最優邊緣分布函數，Ns個Bootstrap子樣本就可以得到Ns個最優邊緣分布函數。為了表征分布類型不確定性，統計4種備選邊緣分布函數被識別為最優邊緣分布的次數。對于參數a來說，Ns=104個Bootstrap子樣本中正態、對數正態、極值I型和威布爾分布被識別為最優邊緣分布的次數分別為94、3 435、3 958和2 513；對于參數b而言，4種分布被識別為最優邊緣分布的次數分別為2 334、5 282、1 048和1 336。可見，在考慮AIC值的變異性時沒有一種備選邊緣分布函數能夠100%被識別為最優邊緣分布。上述結果表明：基于有限試驗數據確定的a和b的邊緣分布函數存在較大的統計不確定性，包括分布參數不確定性和分布類型不確定性。

其次研究Copula函數的統計不確定性。圖6給出了Kendall秩相關系數的概率密度函數。可以看出，基于有限數據估計的Kendall秩相關系數也具有較大的變異性，其變異系數為0.17。Kendall秩相關系數的變異性將導致a和b的Copula函數的相關參數具有統計不確定性，這是因為Copula函數的相關參數是根據Kendall秩相關系數確定的。

圖6 Kendall秩相關系數的概率密度函數Fig.6 Probability density function of Kendall rank correlation coefficient between a and b

圖7給出了4種備選Copula函數AIC值概率密度函數。可以看出，基于有限數據估計的Copula函數的AIC值也具有較大的變異性，Gaussian、Plackett、Frank和No.16 Copula函數的AIC值變異系數分別為0.39、0.39、0.40和0.46。4種備選Copula函數AIC值的變異性將導致a和b的Copula函數類型具有統計不確定性，這是因為Copula函數類型是根據AIC值識別的。此外，4種備選Copula函數AIC值的概率密度函數重疊區域較大，這說明4種備選Copula都有可能被識別為最優Copula函數。下面分析a和b的Copula函數類型不確定性。

圖7 4種備選Copula函數AIC值的概率密度函數Fig.7 Probability density functions of AIC scores for the four candidate copula functions

基于每個Bootstrap子樣本計算的4種備選Copula函數的AIC值即可識別出該子樣本的最優Copula函數，Ns個Bootstrap子樣本可以得到Ns個最優Copula函數。為了表征Copula類型不確定性，統計4種備選Copula函數被識別為最優Copula的次數，可以得出Ns=104個Bootstrap子樣本中Gaussian、Plackett、Frank和No.16 Copula函數被識別為最優Copula的次數分別為2 251、5 233、9 67和1 549。可見，在考慮AIC值的變異性時沒有一種備選Copula函數能夠100%被識別為最優Copula。上述結果表明：基于有限試驗數據確定的a和b的Copula函數存在較大的統計不確定性，包括Copula函數的相關參數不確定性和類型不確定性。

4 基樁正常使用極限狀態失效概率估計

4.1 失效概率計算方法

上面應用Bootstrap方法表征了a和b二維分布模型的統計不確定性，下面進一步給出考慮a和b二維分布模型統計不確定性的基樁正常使用極限狀態失效概率區間估計方法。首先給出基樁正常使用極限狀態失效概率計算方法。

對于基樁正常使用極限狀態來說，當基樁實際位移大于允許位移時認為基樁失效，基樁失效概率計算的功能函數為[5]：

g=ya-y(Q)

(4)

式中：ya為基樁允許位移；y(Q)為外荷載Q時基樁的位移。如果將ya對應的荷載表示為Qa，可得基樁正常使用極限狀態失效概率計算另一種表述方式，即當基樁實際荷載Q大于允許荷載Qa時認為基樁失效，基樁失效概率計算的功能函數為[5]：

g=Qa(ya)-Q

(5)

由于荷載數據比位移數據更加容易獲得，這里采用式(5)計算基樁正常使用極限狀態失效概率，相應的失效概率pf為：

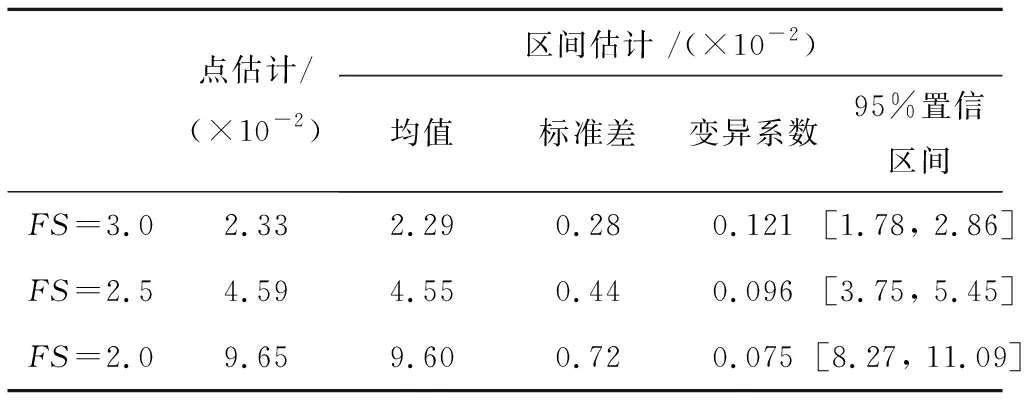
pf=P(Qa(ya)

(6)

將式(1)代入可得：

(7)

從式(7)可以看出，計算基樁正常使用極限狀態的失效概率涉及5個隨機變量：a、b、ya、Q和QSTC。為此，將式(7)進一步表示為：

(8)

4.2 失效概率點估計

在給出基樁失效概率區間估計之前，首先給出傳統方法計算的基樁失效概率點估計。如前所述，基樁失效概率點估計是忽略a和b的二維分布模型統計不確定性或直接采用基于試驗數據建立的二維分布模型的結果。基于雙曲線參數試驗數據，本文第2節建立了a和b的二維分布模型，即a和b的最優邊緣分布函數分別為極值I型分布和對數正態分布，a和b的最優Copula函數為Plackett Copula函數。上述最優邊緣分布函數的分布參數和最優Copula函數的相關參數采用基于試驗數據計算的樣本均值、標準差和Kendall秩相關系數確定。下面給出基樁失效概率點估計結果。

基于本文第2節建立的a和b的二維分布模型，利用蒙特卡洛模擬方法即可計算出基樁失效概率的點估計。表1第2列給出了FS=3.0、2.5和2.0時基樁失效概率的點估計結果。可以看出，基樁失效概率隨FS的減小而增大。基樁失效概率位于10-2量級，可見本文設定的蒙特卡洛模擬次數完全滿足精度要求。此外，忽略a和b的二維分布模型統計不確定性，傳統方法只能得到基樁失效概率的點估計。由本文第3節可知，a和b的二維分布模型具有較大的統計不確定性。因此，基樁失效概率的點估計可能無法真實反映基樁的安全度。針對上述問題，本文提出了基樁失效概率區間估計方法。該方法通過考慮a和b的二維分布模型統計不確定性，得出基樁失效概率的概率密度函數，并將失效概率表示為具有一定置信度水平的置信區間。下面給出該方法的具體實現步驟。

表1 基樁失效概率點估計和區間估計Tab.1 Point and interval estimates of probability offailure of single piles

4.3 失效概率區間估計

本節進一步給出基樁失效概率區間估計。實現基樁失效概率區間估計的關鍵是成功模擬失效概率的概率分布。首先，基于每個Bootstrap子樣本識別的最優邊緣分布函數和最優Copula函數建立a和b的二維分布模型。其次，基于每個Bootstrap子樣本的二維分布模型利用蒙特卡洛模擬方法計算出該子樣本的失效概率，Ns個Bootstrap子樣本就可以得到Ns個失效概率。最后，基于Ns個失效概率采用常規統計方法即可獲得失效概率的均值、標準差、變異系數和概率分布。

圖8以FS=3.0為例給出了基樁失效概率的概率密度函數。由于a和b的二維分布模型統計不確定性的存在，基樁失效概率具有明顯的變異性，如FS=3.0時基樁失效概率的變異系數達到了0.121。為了表征基樁失效概率的變異性，本文將基樁失效概率表示為具有一定置信度水平的置信區間。為了簡單起見，將基樁失效概率的97.5%和2.5%分位數分別作為基樁失效概率的95%置信區間的上下限。表1給出了基樁失效概率區間估計結果，包括基樁失效概率均值、標準差、變異系數和95%置信區間。與傳統方法計算的基樁失效概率點估計相比，由于考慮了a和b的二維分布模型統計不確定性，基樁失效概率區間估計能夠更加合理地表征基樁的真實可靠度水平。

圖8 基樁失效概率的概率密度函數Fig.8 Probability density function of probability of failure of single piles

為了研究FS對基樁失效概率置信區間的影響，圖9給出了基樁失效概率的95%置信區間隨FS的變化曲線。為了比較，圖中還給出了基樁失效概率的點估計。可以看出，基樁失效概率95%置信區間的上下限隨FS的降低而增加，基樁失效概率置信區間的變化范圍亦隨FS的降低而增大。基于傳統方法計算的基樁失效概率的點估計只能反映基樁的平均可靠度水平，而不能給出基樁失效概率的變異系數及其上下限。與其相反，基樁失效概率區間估計方法能夠有效得到基樁失效概率的概率分布及其置信區間。這種置信區間不僅能夠更加準確地表征基樁的可靠度，而且便于工程設計人員進行基樁的加固設計。這是因為工程設計人員能夠方便地看到基樁失效概率的上下限隨FS的變化關系。

圖9 基樁失效概率隨FS的變化曲線Fig.9 Variation of probability of failure of single piles with factor of safety

5 結 語

(1)基于有限雙曲線參數試驗數據估計的樣本均值、標準差、Kendall秩相關系數和AIC值具有較大的變異性，這種變異性進一步導致雙曲線參數的二維分布模型存在明顯的統計不確定性。

(2)Bootstrap方法通過模擬雙曲線參數統計量的變異性，有效地表征了雙曲線參數二維分布模型的統計不確定性。該方法只需已知雙曲線參數試驗數據，為有限數據條件下統計量變異性模擬和統計不確定性表征提供了一條有效的途徑。

(3)雙曲線參數二維分布模型的統計不確定性對基樁失效概率的估計具有重要的影響。有限數據條件下基樁失效概率具有顯著的變異性。為了減小基樁失效概率的變異性，建議增加雙曲線參數試驗數據的樣本數目。

(4)通過考慮雙曲線參數二維分布模型的統計不確定性，基樁失效概率可以表示為具有一定置信水平的置信區間，而不是傳統方法的點估計。基樁失效概率的區間估計相比點估計能更加合理地表征基樁的真實可靠度水平。