基于遞進復合式組合預測模型的軟巖隧道大變形預測研究

趙淑敏

(陜西鐵路工程職業技術學院， 陜西 渭南 714000)

0 引言

隨著我國公路建設的快速發展，隧道大變形已成為常見的施工災害[1]，對安全施工造成了較大的隱患。對其變形預測，能有效指導現場的變形預警和施工優化，研究意義明顯。隧道大變形是由多種因素共同作用造成的，內因和外因都不可或缺[2]。在大變形的研究方面： 駱文學[3]采用有限差分的數值模擬對隧道大變形特征進行分析，得到軟弱破碎帶地質環境大變形規律，為該地質條件下的支護設計提供了參考。在隧道的變形預測方面： 李曉龍等[4-5]利用最小二乘法優化的支持向量機模型進行預測，得出最小二乘法對支持向量機的參數優化效果較為明顯，提高了支持向量機的預測性能，預測效果較好； 黃志波等[6]將BP神經網絡引入到大斷面隧道的變形預測中，通過實例驗證該方法的預測精度能滿足工程需要，對現場施工能進行有效的指導； 謝齊等[7]和賴祖龍等[8]將灰色模型和BP神經網絡進行結合建模，得出的預測結果與實測值間的差異較小，預測精度較高，適用性較強。但以上多是采用單一模型進行預測，且缺少在隧道大變形方面的預測研究； 同時，變質巖隧道具有其特有的地質條件，也缺少相應的變形預測研究。該文以支持向量機、灰色模型為基礎，采用最小二乘法對2種方法進行參數優化，確定2種單項預測模型； 其次，以誤差平方和為評價指標，確定組合權值，實現組合預測，并利用BP神經網絡修正組合預測誤差，以進一步提高預測精度。該文旨在通過2階段遞進預測，構建隧道大變形的二階復合式預測模型，以期提高預測精度，并結合實例來探討該模型的適用性和有效性。

1 基本原理

基于LS-SVM、優化GM(1,1)和BP神經網絡的二階復合組合預測模型的預測流程如圖1所示。該模型的基本思路是： 充分發揮各參與模型的優勢，將預測風險最小化，以增加預測模型的精度及穩定性，即首先利用LS-SVM和優化GM(1,1)模型對隧道變形監測數據進行預測，并采用誤差平方和倒數法將兩者的預測結果進行組合； 再進一步利用BP神經網絡對兩者的組合結果進行誤差修正，以進一步提高預測精度，進而綜合建立變質巖隧道的二階復合式組合預測模型。

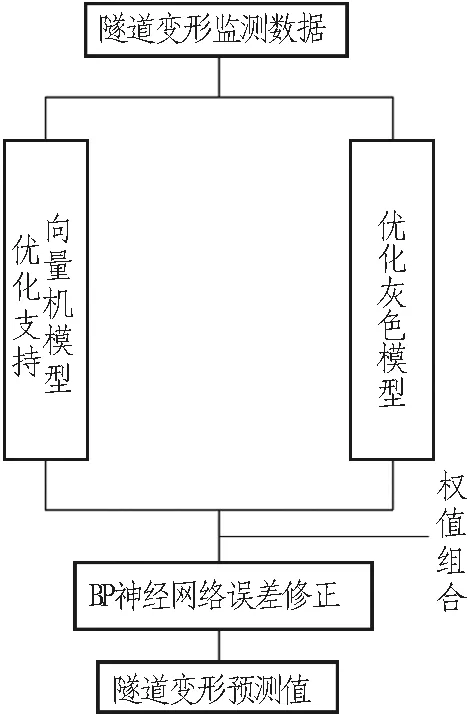
圖1 二階復合組合預測模型

結合本文工程實例，二階復合式組合預測模型的預測步驟分述如下。

1)利用LS-SVM和優化GM(1,1)模型對隧道的拱頂沉降變形進行預測，并對比優化前后預測結果的差異，以探討優化方法的有效性； 同時，以誤差平方和為評價指標，確定組合權值，對兩預測模型的預測結果進行組合。誤差平方和及權值計算公式如式(1)和式(2)所示。

(1)

(2)

式中：wi為第i種方法的組合權值； SSEi為第i種方法的誤差平方和；m為單項預測方法的個數。

2)利用BP神經網絡對前者預測結果進行誤差修正，以進一步提高預測精度，達到綜合預測的目的，進而得到隧道拱頂沉降的變形預測值。

3)將本文預測模型再應用到隧道的周邊收斂變形預測中，以檢驗本文預測模型的有效性，且通過對比隧道拱頂及周邊的預測結果，對隧道后期的變形趨勢進行分析，為現場施工提供依據。

1.1 支持向量機模型

支持向量機的學習方法及識別模式均是由統計學理論發展而來，采用結構風險最小化的原則，具有很好的泛化能力，對小樣本也能實現很好的非線性預測[9-11]。

若隧道變形的樣本表示為{xi,yi}，通過非線性映射將x映射到高維空間，進而構建出線性回歸函數

f(x)=ωφ(x)+b。

(3)

式中：f(x)為回歸表達式；φ(x)為非線性映射函數；ω為權重慣量；b為偏置量。

基于風險最小化原則，在超出ε條件下，引入松弛變量ξi、ξi*(ξi≥0、ξi*≥0)，則可將上述回歸映射問題轉變為：

(4)

(5)

式(4)和式(5)中：L(x)為Lagrange函數；b為偏置量；l為訓練樣本數；ω為權重慣量；ε為不敏感損失函數(將其設定為0.6)；C為懲罰因子。

根據對偶理論，將式(4)的優化問題轉變為二次規劃問題對偶問題，即：

(6)

(7)

式中：αi、αi*為拉格朗乘子；K(xi,yj)為核函數。

通過對式(6)的最終求解，可以得到回歸函數

(8)

式中： 偏置量由KTT條件求得，且αi-αi*≠0為對應xi的支持向量。

核函數、核參數及正則化參數對支持向量機模型的預測性能具有較大影響，而上述參數又是由模型設計者設定，具有較大的主觀性，對使用者的經驗要求較高。因此，本文引入最小二乘法對支持向量機的參數進行優化，實現原模型由不等式約束到等式約束的轉變，進而降低求解難度。結合實例特點，將優化過程分述如下。

1)支持向量機的核函數有3種，即徑向基核函數、多項式核函數及線性核函數，其中，徑向基核函數的非線性預測能力相對更強[12]，能有效解決復雜的非線性問題，故將其作為本文支持向量機模型的核函數。

2)通過網格化劃分，對核參數及正則化參數進行網格取值，并利用最小二乘法采用交叉驗證的手段篩選出最優參數組合。通過最小二乘法對參數的優化能有效避免多解性問題，得到最優的互偶解，且將兩參數的優化區間均設定為[0,1010]，網格點數為1010×1010，步長均為1。

3)將最小二乘法優化得到參數帶入到支持向量機模型中，建立優化支持向量機模型。在尋優之初，將核參數及正則化參數分別初始設定為0和1，經過尋優，得到最優核參數為51，最優正則化參數為 4 152 637。

1.2 灰色模型

灰色模型是基于模糊理論發展而來的，通過對少量或不完全信息的收集達到對事物發展規律進行長期預測的目的，對小樣本數據的預測能力較強，已被廣泛地應用和研究[13-14]。若隧道變形的初始樣本為x(0)，即

x(0)(k)={x(0)(1),x(0)(2),…,x(0)(n)}。

(9)

式中k=1,2,…,n(n為樣本個數)。

由于隧道原始監測樣本具有波動性和隨機性，采用一階累加進行處理，處理后序列為x(1)，即

x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}。

(10)

其中，式(10)對應節點的求解過程為

(11)

而一階累加序列應滿足階微分方程

dx(1)(t)/dt+ax(1)(t)=b。

(12)

式中：a、b參數與初始序列相關，且滿足最小二乘法估計，即

(13)

通過對上述微分方程的求解，其特解即可反推出各節點的預測值，即

x＾(0)(k+1)=x＾(1)(k+1)-x＾(1)(k)(k=1,2,…,n)。

(14)

由于傳統灰色模型受輸入序列隨機性的擾動較大，易導致預測過程中的穩定性及系統誤差缺陷。為避免上述問題對預測精度的影響，本文再次將最小二乘法引入到灰色模型的優化過程中。在優化過程中，主要是考慮一階累加序列的初始值具有一定的不合理性，且隨著序列累加階次的增加，初始值與預測值間的相關性會進一步減弱，進而影響預測模型的精度。因此，本文采用最小二乘法確定初始值，先設定

(15)

式(15)中只要求得c值即可得到初始值的最優估計值，結合最小二乘法原理，式(15)應滿足

(16)

通過式(16)對c的求導，即可得到

(17)

通過上述計算，最終確定一階累加序列的初始值，以達到增加灰色模型穩定性的目的。經優化處理，得到a為2.41，b為4.18。

1.3 BP神經網絡

BP神經網絡是前饋神經網絡，具有多層結構，一般可分為3層(見圖2)，分別為輸入層、隱含層和輸出層，其中各層的節點可根據實例進行設定，且各層間的節點由對應權值進行連接。BP神經網絡的傳播過程包含了正向傳播和反向傳播，其中，正向傳播指的是輸入信息由輸入層傳至隱含層，再傳至輸出層，并對比期望結果。若不滿足要求，則進入反向傳播，對各節點權值進行修正，直到輸出結果滿足期望要求。

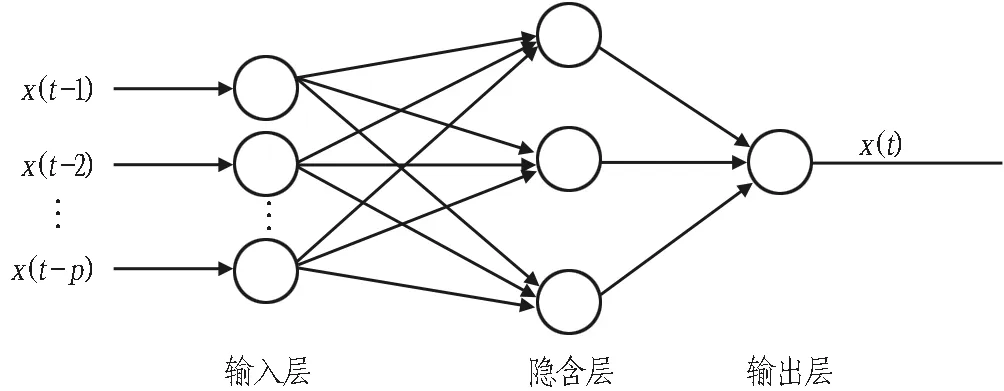
圖2 BP神經網絡結構圖

根據BP神經網絡信息傳播過程，將其預測過程分述如下。

1)BP神經網絡的結構為遞推型結構，將輸入層節點數設定為6，輸出層節點數為1，即以1—6周期預測第7周期； 以2—7周期預測第8周期，以此類推。同時，對模型參數進行設定，如將訓練函數設置為train()函數、仿真函數設置為sim()函數、建立函數設置為newff()函數、隱層節點數為10、初始閾值范圍為[0,1]等。

2)根據隧道變形的樣本信息，將訓練樣本輸入輸入層Pk，并正向訓練傳播至輸出層Tk，得到網絡訓練的輸出值Tk*。

3)采用梯度法對各層間的連接權值進行修正，并將輸出值與期望值之間的誤差表示為

(18)

而權值調整由修正函數確定，即

ωij=ωij+Δωij=ωij+ηδqiγqi。

(19)

式中：δqi為誤差修正系數；η為學習因子；i為隱層或輸出層節點；q為第q個學習樣本。

4)若訓練誤差達到期望的收斂誤差，則停止訓練；若訓練誤差未達到收斂誤差，則進入誤差反向傳播階段，即重復進入第3步，直到輸出結果達到期望要求。

2 實例分析

2.1 實例概況

為驗證本文預測模型的有效性，以通省隧道為實例來源[15]，對其變形進行預測。該隧道軸向為235°，屬變質巖隧道，圍巖為武當群片巖，片理化發育程度較高，是目前國內最長的變質巖隧道，對其變形進行研究具有重要的意義； 同時，圍巖的變形具有明顯的時間效應特征，大變形時有發生，如右洞YK110+510～+519區間在2012年5月26日出現局部掉塊，并引發了施工問題，故對該大變形區間的變形預測具有重要的意義。典型斷面YK110+515的監測數據如圖3所示。

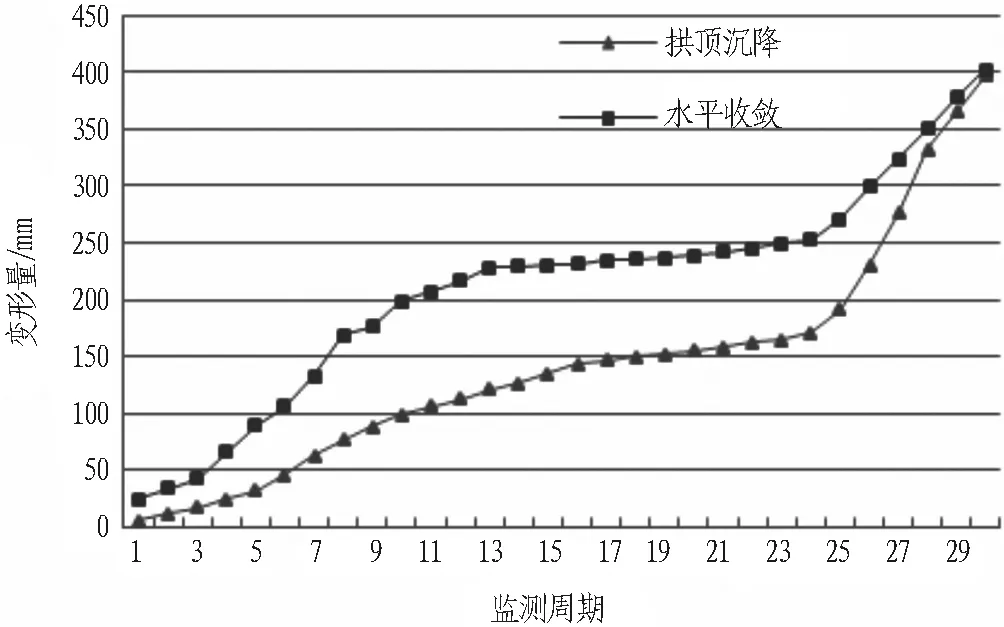
圖3 YK110+515斷面變形曲線

由圖3可以看出： 1)拱頂及水平變形均具有“S”曲線的特征，在12—22周期的變形均相對較平緩，但在后期變形出現了明顯的增加，這與下臺階施工擾動相關； 2)對比拱頂與水平變形的特征，水平變形量均不同程度地大于拱頂沉降量，得出隧道變形以水平收斂為主，分析其原因主要是由隧道下臺階未施工，造成初期支護未封閉引起的。

為進一步分析隧道大變形特征，再對其變形速率進行統計。大變形變形速率特征如表1所示，YK110+515斷面變形速率曲線如圖4所示。

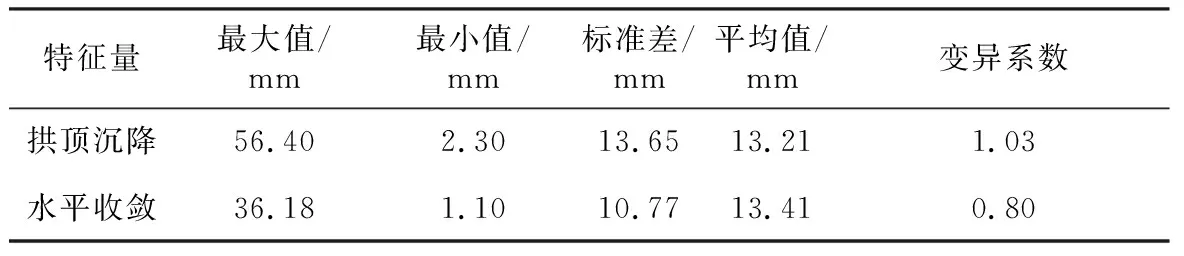
表1 大變形變形速率特征表

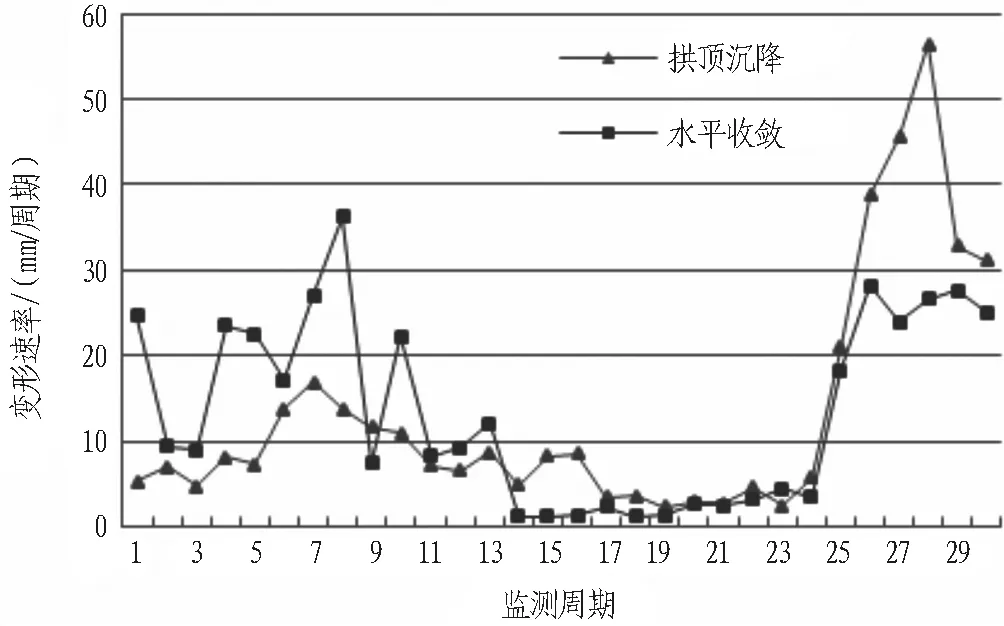
圖4 YK110+515斷面變形速率曲線

由表1和圖4可以看出： 1)拱頂沉降和水平收斂變形速率均具有較大的波動性，且在前期以水平收斂的波動性相對更強，在后期則以拱頂沉降的波動性相對更強，說明在隧道大變形的發展過程中，隧道圍巖的應力分布出現了變化； 2)對比拱頂和水平變形的特征參數，得出水平收斂變形較拱頂沉降變形具有相對更小波動性，穩定性相對更好，且拱頂沉降的變異系數為1.03，水平收斂的變異系數為0.8，也進一步說明水平收斂變形的游離性更弱。

2.2 變形預測

采用支持向量機和灰色模型對拱頂沉降進行變形預測，其中，支持向量機也采用遞進預測結構，輸入節點數仍為6，輸出層節點數仍為1； 而灰色模型采用全樣本預測，預測結果如表2所示。可以看出： 1)對比各模型的預測精度，具有一定的差異，從側面可證明本文通過二階復合結構增加預測模型穩定性的必要性； 2)對比2種模型在優化前后的預測結果，得出通過參數優化，均不同程度地提高了預測精度，說明最小二乘法對2種模型的優化達到了預期目的。

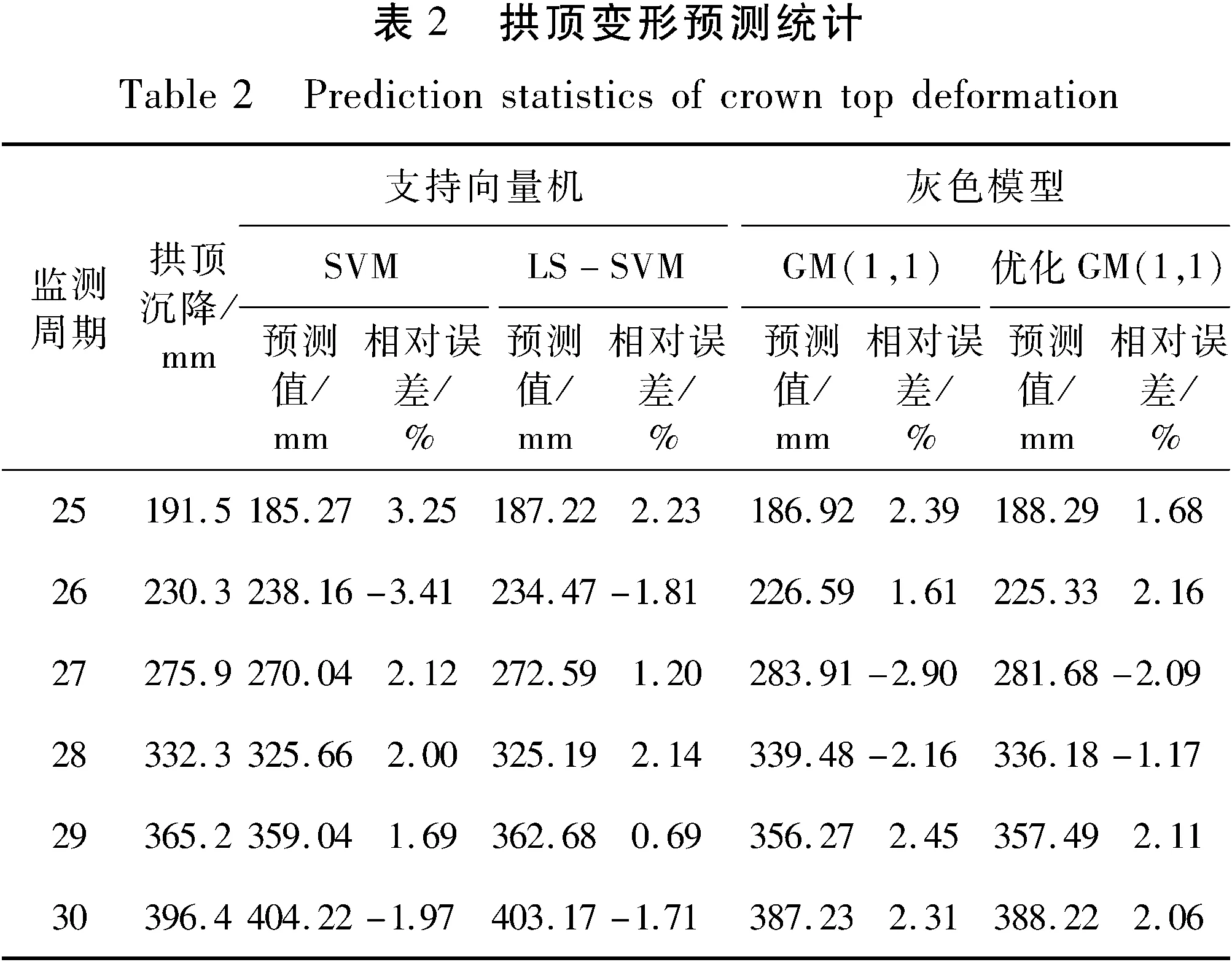
對表2中各模型預測結果的相對誤差平均值和方差進行統計，結果如表3所示； 并對預測誤差進行對比統計，結果如圖5所示。由表3和圖5可以看出： 1)對比各模型預測結果相對誤差的均值，得出LS-SVM模型的效果最優，均值為1.63%，其次是優化GM(1,1)模型、GM(1,1)模型和SVM模型，且最小二乘法對2種基礎模型的預測精度均有一定的提高，但支持向量機模型要優于灰色模型的優化效果，前者提高0.78%的預測精度，而后者提高了0.42%，說明通過最小二乘法能有效地優化預測模型參數，達到提高預測精度的目的； 2)對比各預測模型預測結果的方差，可以得出灰色模型較支持向量機預測結果的穩定性更好，其中，優化GM(1,1)模型的穩定性最佳，方差值為0.151 9，其次是GM(1,1)模型、優化SVM模型和SVM模型； 3)對比各預測模型的預測誤差，得出各模型預測結果的差異性較明顯，在相同節點具有相反的預測誤差值。因此，綜合得出優化支持向量機模型具有較高的預測精度，但預測結果的穩定性較弱，而優化灰色模型具有相反的特點，進而本文采用組合方法，將2種優化模型的結果進行組合，組合權值是以誤差平方和為指標，分別為0.584 1和0.415 9。

表3拱頂變形預測特征參數統計

Table 3 Statistics of characteristic parameters of crown top deformation prediction

預測方法平均值/%方差SVM2.410.536 5LS-SVM1.630.346 6GM(1,1)2.300.177 5優化GM(1,1)1.880.151 9

通過上述基礎預測，再利用BP神經網絡對上述預測結果進行修正預測，結果如表4所示。可以看出： 1)通過組合權值的綜合，得到組合后預測結果的相對誤差均值為0.75%，方差值為0.581 6，得出通過組合預測能較好地提高預測精度，但對預測結果的穩定性提高不大，而通過誤差修正的相對誤差均值為 0.38%，方差值為 0.167 6，相對前者，預測精度提高了1.97倍，預測結果的穩定性則提高了3.47倍，說明通過誤差修正，能較為明顯地提高預測精度及穩定性，驗證了本文修正模型的有效性； 2)通過對31—34周期的變形預測，得到隧道拱頂后4個周期的變形呈增長趨勢，且變形速率相對較大。

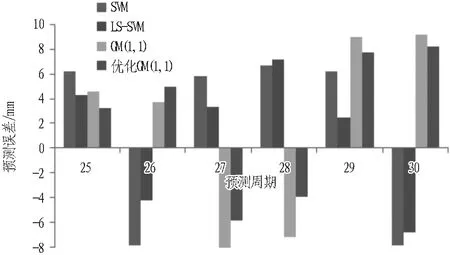
圖5 拱頂變形預測誤差對比

Fig. 5 Comparison between prediction errors of crown top deformation

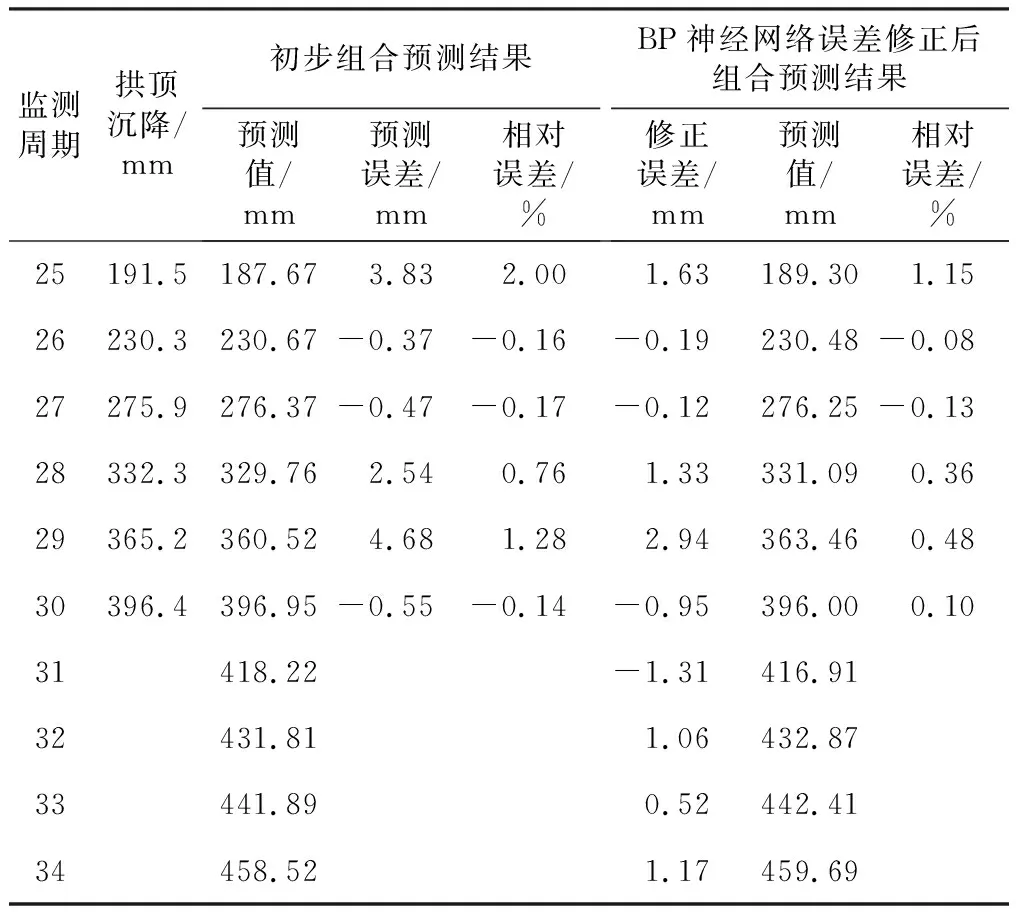
表4 誤差修正預測

2.3 有效性檢驗

為進一步驗證本文預測模型的有效性，本文再以該斷面的周邊變形收斂數據為基礎，采用本文模型進行預測分析，結果如表5所示。可以看出： 1)通過周邊變形預測，得到前期預測結果的最大相對誤差為1.67%，相對誤差平均值為1.34%，方差值為 0.160 2，而誤差修正后的最大相對誤差為1.32%，相對誤差平均值為0.72%，方差值為0.128 0； 2)對比誤差修正前后的預測結果，得出修正后提高預測精度和方差分別為1.86倍和1.25倍； 3)對后4個周期的變形預測，得出周邊變形仍是呈增長趨勢，且增長速率均保持在10 mm/周期之上，34周期的最大變形量已達446.19 mm。

表5周邊收斂變形預測統計

Table 5 prediction and statistics of surrounding convergence defor-mation

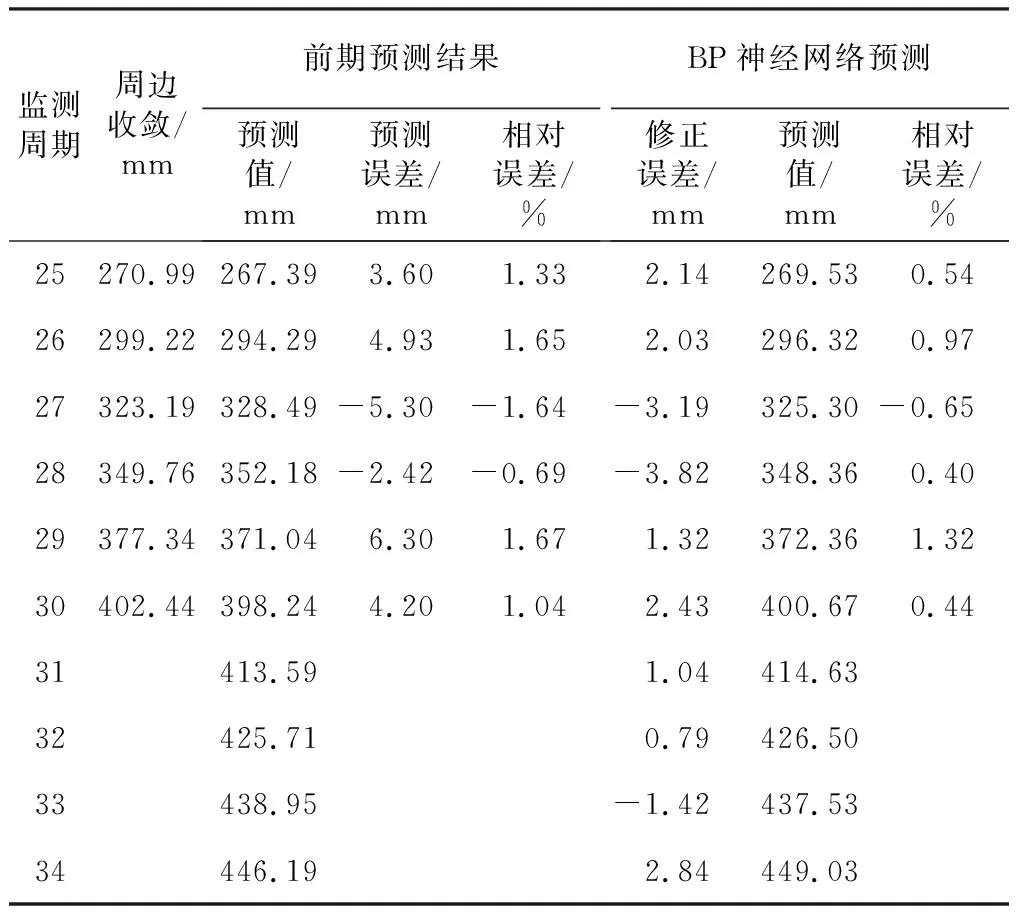
監測周期周邊收斂/mm前期預測結果預測值/mm預測誤差/mm相對誤差/%BP神經網絡預測修正誤差/mm預測值/mm相對誤差/%25270.99267.393.601.332.14269.530.5426299.22294.294.931.652.03296.320.9727323.19328.49-5.30-1.64-3.19325.30-0.6528349.76352.18-2.42-0.69-3.82348.360.4029377.34371.046.301.671.32372.361.3230402.44398.244.201.042.43400.670.4431413.591.04414.6332425.710.79426.5033438.95-1.42437.5334446.192.84449.03

統計該斷面拱頂及周邊的變形預測誤差，結果如圖6所示。可以看出： 1)周邊變形預測結果的誤差值相對更大，且波動性更強，進而拱頂預測的效果相對更優； 2)分析后4個周期的變形預測結果，綜合得出該斷面在后期仍具有持續變形的特征，圍巖穩定性將進一步減弱，圍巖塌方的可能性較大，應采取措施，避免引發的工程施工問題。

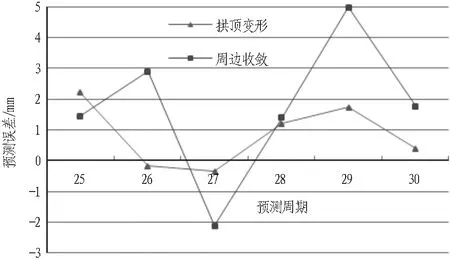
圖6 拱頂與周邊收斂變形預測誤差對比

Fig. 6 Comparison of prediction error of convergence deformation between crown top and surrounding

3 結論與討論

1)通過最小二乘法對支持向量機和灰色模型的優化，構建了兩者的優化模型，增強了預測模型參數的準確性，提升了預測模型的預測能力。

2)通過實例驗證，得出最小二乘法對支持向量機的優化效果要優于對灰色模型的優化效果，但在預測結果的穩定性方面，優化的灰色模型則具有更高的穩定性，說明不同模型之間的預測結果間具有互補性。

3)在拱頂變形預測的誤差修正中，預測精度提高了1.97倍，穩定性提高了3.47倍； 而在周邊變形預測的誤差修正中，預測精度提高了1.86，方差提高了1.25倍。對比而言，前者的誤差修正效果相對更優。

4)綜合實例分析的結果，得出本文預測模型具有較高的預測精度及穩定性，且通過了有效性檢驗，進一步得出本文模型的適用性較廣，值得廣泛推廣和深入研究，但該文預測模型在其他巖土領域中的適用性仍需進一步研究。