信道相關情況下UHF RFID識別性能分析

佘開，何怡剛，李兵，朱彥卿

?

信道相關情況下UHF RFID識別性能分析

佘開1，何怡剛2，李兵2，朱彥卿3

（1. 湖南科技大學物理與電子科學學院，湖南 湘潭 411201；2. 武漢大學電氣工程學院，湖北 武漢 430072；3. 湖南大學電氣與信息工程學院，湖南 長沙 410082）

針對UHF RFID系統識別率受電波多徑傳播制約的問題，研究了前向與反向相關信道對系統識別性能的影響。將信道分為獨立、相關和完全相關3種情形，基于廣義萊斯衰落信道模型，推導了識別率的解析計算式。與現有分析相比，此分析給出了任意相關系數和多種信道條件下識別率統一的計算式。仿真實驗表明，不同相關系數、信道條件、靈敏度和距離對識別率有影響。

射頻識別技術；識別率；相關信道；廣義萊斯衰落模型

1 引言

超高頻射頻識別（UHF RFID）系統具有無源、識別距離遠、多標簽識別和成本低等優點，在物流、倉儲和智能交通等領域具有廣闊的應用前景。該技術基于雷達原理，單標簽識別率由閱讀器至標簽無線供電的芯片激活概率以及標簽至閱讀器的反向散射通信成功率共同決定。各類應用場景的無線信道模型、信道間相關特性、標簽芯片靈敏度等都對識別率有很大影響[1]。故本文考慮實際應用場景中的各種影響因素，特別是信道相關系數，研究標簽識別率的計算方法。

文獻[2]首先對辦公室環境下RFID系統的反向散射調制信道進行了測量，指出小尺度衰落可由2個萊斯（Rician）隨機變量的乘積建模，而大尺度路徑損耗是單個路徑損耗的2倍。文獻[3]隨后對鏈路預算方法進行了實驗與理論研究，采用多線模型對路徑損耗進行分析，測試了視距與非視距情形下大尺度路徑損耗因子的值，并分別采用Rician和瑞麗（Rayleigh）分布建模小尺度衰落。文獻[4]將影響標簽與閱讀器接收功率的因素參數化，提出了改進的Friis模型，用于識別范圍的估算。文獻[5]基于菲涅耳區理論，分析并測試了菲涅耳余隙對路徑損耗與識別距離的影響。文獻[6]針對RFID系統反向鏈路，對閱讀器接收標簽信號信噪比和誤碼率進行了推導，得出了Nakagami-信道在干擾情形下的識別距離表達式。文獻[7]對級聯RFID反向信道與干擾對RFID系統識別性能進行了詳細分析，給出了識別率在理想環境、多徑環境、干擾環境下的計算式和仿真結果。

上述研究都是將前向和反向信道作為獨立的信道進行分析的，并沒有考慮兩者間相關系數對識別性能的影響。因此，文獻[8]對RFID的相關信道特性進行了研究，基于2個相關Rayleigh隨機變量的聯合分布函數，僅給出了反向信道誤碼率的數值結果。文獻[9]對采用發射分集的UHF RIFD系統識別性能進行了研究，構造了相關的前向和反向信道Rician或Rayleigh隨機變量，通過仿真指出發射分集增益隨著前向和反向信道相關性的增加而增加，隨著編碼冗余和前向鏈路間相關性的增加而減小，但其并未給出識別性能或分集增益的顯式計算式。而文獻[10]基于相關的Rician信道特征函數的等價表達式，給出了采用多天線分集技術的閱讀器在大信噪比下的誤碼率的漸進展開式，但僅考慮了單一Rician信道情形。-和-分布因其廣泛的信道代表性而在級聯（或中繼）的多徑信道誤碼率分析中越來越受關注[11]，文獻[12]采用這2種分布建模UHF RFID相關信道，給出了識別率的計算式和數值結果，但并不能同時適用獨立和完全相關這2種特殊情形。

綜上，目前關于相關系數對識別率的影響研究，都是關于反向級聯信道誤碼率的解析表達式，而識別率是由前向激活鏈路與反向散射鏈路共同決定的；并且現有文獻都是基于多天線接收在單一衰落信道下推導的，沒有涵蓋多種信道條件的統一表達式。故本文基于廣義Rician信道模型，考慮相關系數的3種取值情形，研究識別率的統一解析表達式，為理論分析與實驗仿真UHF RFID系統識別可靠性提供一種有效的方法。

2 標簽識別概率

標簽識別概率可簡單分為單標簽識別概率與多標簽識別概率，兩者均是UHF RFID系統非常重要的性能指標。因為多標簽識別概率除了取決于預計識別區域內可靠的射頻通信之外，還與預計識別區域的范圍和防碰撞通信協議的效率有關。前者是后者的基礎，故本文僅對單標簽識別率進行研究。

單標簽的成功識別取決于前向信道能否激活標簽芯片，即標簽接收功率是否大于芯片激活閾值（此時由于標簽接收信號信噪比很高，認為無前向解碼錯誤），同時，還取決于閱讀器能否正確解碼標簽反向散射的信號。后者一般通過一定信噪比下的誤碼率來度量反向信道的識別性能[6-9]。

為了同時考慮上述2個因素，并準確給出單標簽識別概率表達式，采用閱讀器接收信號是否大于其靈敏度的方式來描述反向信道的通信成功率。故預計識別范圍內單標簽識別概率（）可以定義為

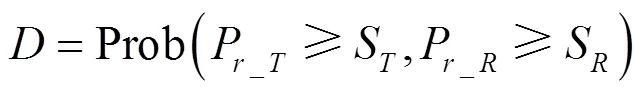
其中，P為經過前向信道（閱讀器至標簽）衰落后標簽的接收功率；P為標簽散射信號經反向信道（標簽至閱讀器）由閱讀器接收的功率；S為標簽激活靈敏度；S為閱讀器在一定誤碼率下的靈敏度。

標簽接收功率[4,7]（P）為

其中，P為閱讀器發射功率；ρ為閱讀器與標簽天線間極化匹配失配因子；G和G分別為閱讀器與標簽天線增益，取決于其本身的電氣屬性，并與兩者間的空間相對位置（方位角）有關，當只考慮單標簽識別率時，認為其為定值；(d)為兩者相距d時的大尺度路徑損耗；h為小尺度衰落隨機系數。根據目前UHF RFID相關標準所定義的通信速率、標簽移動速度及應用場景等參數，可確定其前向和反向信道小尺度特性都屬于平坦衰落和慢衰落信道，因此可以采用服從Rician分布（視距）、Rayleigh分布（非視距）或Nakagami-分布的單變量（非時變）進行建模。

當P達到標簽芯片激活閾值S后，標簽通過反向散射調制方式向閱讀器發送數據，閱讀器接收的散射功率[4,7]（P）可表示為

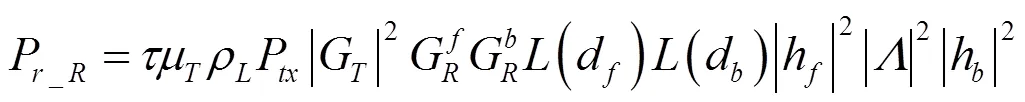
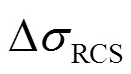
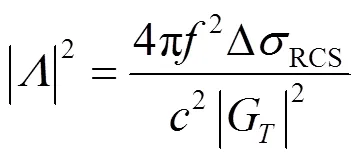
其中，為光速，為頻率。

3 信道模型

由第2節的分析可知，前向和反向信道統計模型及聯合概率密度函數決定標簽識別率，故本文問題轉化為式(5)的求解。

采用文獻[13]中的方法構造隨機變量

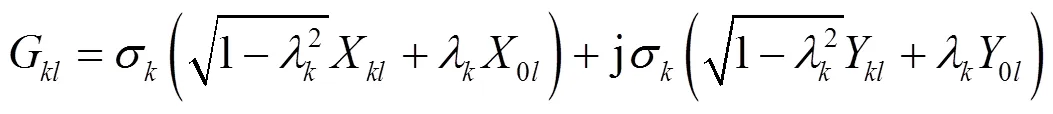
若令

那么h則為廣義Rician隨機變量，且h=|h|，兩兩間相關系數可由式(6)確定。并且二維的廣義Rician分布聯合概率密度函數可表示為[13]

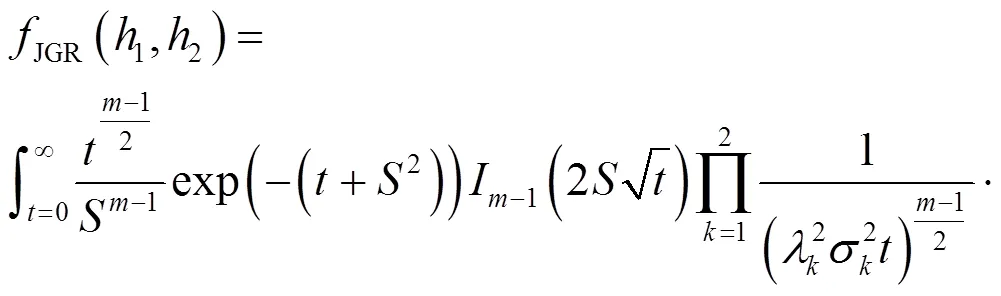
1) 取=1，≠0，h即為相關的Rician分布隨機變量。

2) 取=1且1l=2l=0或=0，h即為相關的Rayleigh隨機變量。

3) 當≠1且1l=2l=0或=0，h即為相關的Nakagami-隨機變量。

并且式(9)可分別化簡為相應的隨機分布的概率密度函數。

值得注意的是，兩廣義Rician隨機變量間的相關系數與的關系并無顯式表達式，本文在實驗部分基于蒙特卡洛方法，以典型數值方式列出了其關系。

4 相關系數對識別率的影響

1) 0<||<1

其中

利用文獻[14]中的計算式，有

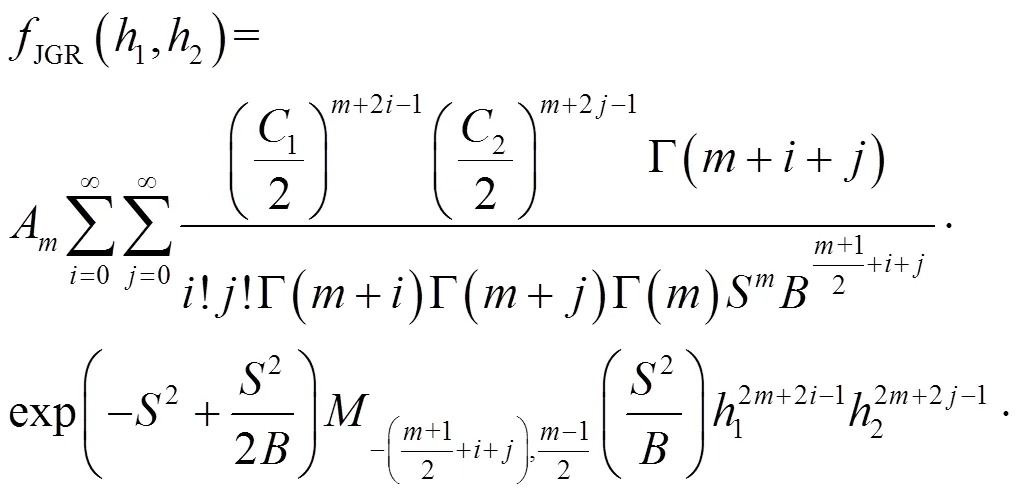
基于積分計算式[14]，有

(15)

因此，最終的識別率的計算式可表示為

通過積分和特殊函數的級數展開與求積分運算，識別率的計算復雜度為兩重無限求和運算，與已有結論[7-12]的計算復雜度一致。

特別地，當式(16)中取=1時，得到Rician信道下的識別率計算式。

令=0，式(16)中Whittaker函數根據文獻[14]，得到Nakagami信道下的識別率為

基于式(17)，再取=1，即得Rayleigh信道下的識別率計算式。

2)=0

Marcum Q函數可展開為[15]

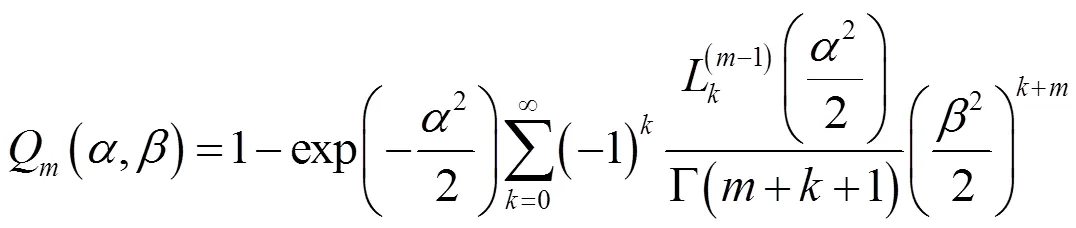
若≠0，則將式(21)貝塞爾函數用級數形式展開，并求積分后，有

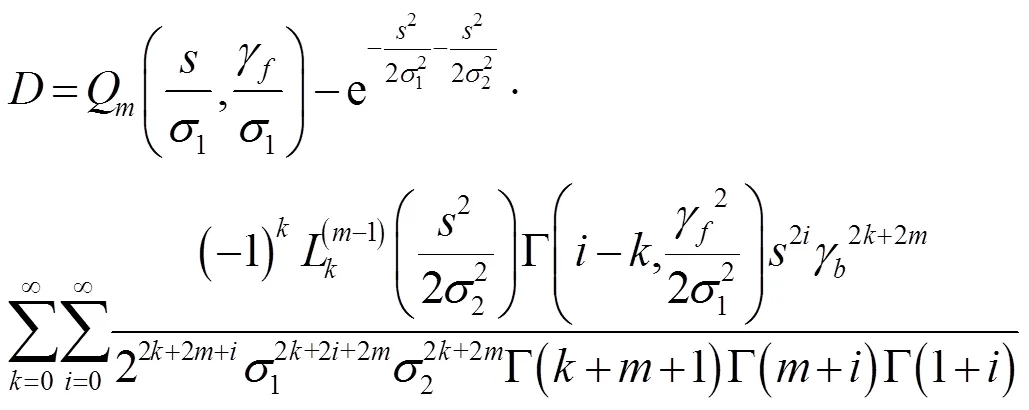
式(22)可用于計算廣義Rician信道（>1，≠0）和Rician信道（=1，≠0）的識別率。若=0，式(21)可進一步化簡為

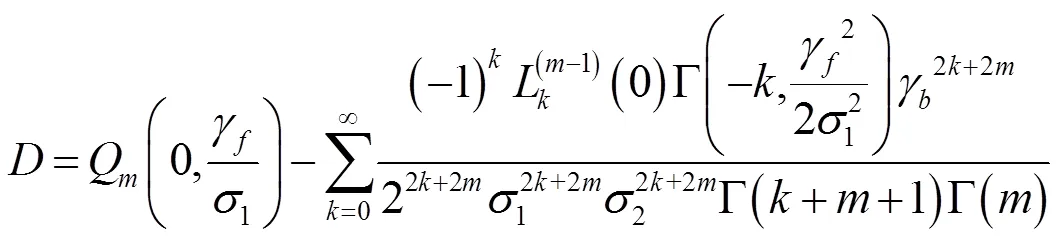
式(23)可用于計算Rayleigh信道（=1，=0）和Nakagami-信道（>1，=0）的識別率。這樣，式(19)中的二重積分被表示為二重（或一重）求和形式，得到前向與反向信道獨立情形下識別率的解析表達式。

3) ||=1

此時，認為h=h，即閱讀器采用單站天線方式，前向和反向信道為同一信道，故識別率可表示為

5 實驗研究

參考國家標準GB/T 29768-2013及文獻[7]中射頻參數的取值，仿真參數如表1所示。采用本文推導結果計算，得出各種條件下識別率隨距離的變化曲線。同時采用蒙特卡洛方法，基于式(5)和式(6)，通過生成2個相關廣義Rician隨機變量的106個樣本值，獲得識別率的仿真值。仿真時通過給定參數和的值，得到3種相關信道下的識別率。

表1 仿真射頻參數

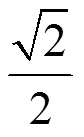
實驗結果表明，本文給出的識別率計算結果與蒙特卡洛仿真結果完全吻合。若要求識別率大于90%，各種信道下的最大識別距離均不同，例如，對于=1的情形，約為6.5 m（Rayleigh）和9 m（Rician和Nakagami-），并且需位于閱讀器天線的最大輻射方向。由于存在視距，Rician信道的識別率高于Rayleigh信道；而對于Nakagami-信道，雖然沒有視距存在，但因為=2，相當于是4個零均值實高斯隨機變量的RSS（root sum square），即前向和反向信道都獲得了分集增益[6]，故其識別率在相關情形一直高于Rician信道，而在其他2種情形的主要識別區域（d<10 m）也略高于Rician信道。

圖1 3種相關系數情形下的識別率隨閱讀器標簽間距變化情況

對于單站UHF RFID系統，閱讀器標簽間的視距一般都存在，故大多數情況下都是前向信道受限，識別率主要取決于標簽靈敏度。但是，對于雙站天線系統，可能存在前向視距而反向非視距的情形，或標簽位于閱讀器發射天線主瓣及接收天線旁瓣方向，故也可能為反向鏈路受限，此時識別率取決于閱讀器靈敏度。

因此，針對Rician信道（取=1，=1），圖2給出了3種相關情形下，識別率隨標簽和閱讀器靈敏度變化的曲線。計算時，取識別距離d=d=5 m，其他參數如表1所示。

實驗結果表明，3種相關情形下，隨著標簽和閱讀器接收靈敏度的減小，識別率均呈降低趨勢，且對于閱讀器靈敏度在?90~?70 dBm范圍內變化時，識別率曲線相差不大，但隨著閱讀器靈敏度的進一步減小，識別率的下降呈加快的趨勢。圖2(a)的||=1情形，對于不同的閱讀器靈敏度，識別率首先隨標簽靈敏度并沒有變化，這是因為此時標簽靈敏度較高，前向和反向信道為同一信道，識別率完全由閱讀器靈敏度決定，隨著標簽靈敏度的降低，在?18 dBm（當S=?80 dBm）和?12 dBm（當S=?70 dBm）處，識別率變成由標簽靈敏度決定了；對于其他情形，除非閱讀器靈敏度特別差（如S=?60 dBm或?50 dBm），識別率都由標簽靈敏度決定，故采用雙站收發天線時，更應該盡量提高標簽靈敏度。

針對Rayleigh、Rician和Nakagami-這3種信道，圖3給出了不同信道相關參數下識別率隨閱讀器標簽間距變化的情況。計算時，取典型值S=?70 dBm，S=?13 dBm，其他參數如表1所示。

值得注意的是，式(6)和文獻[10]中只給出了生成的復高斯隨機變量G間的相關系數，而由此派生的廣義Rician隨機變量H間的相關系數并未給出。故本文通過蒙特卡洛方法，列出了相關系數與典型值的關系，其中，1=2=1，如表2所示。

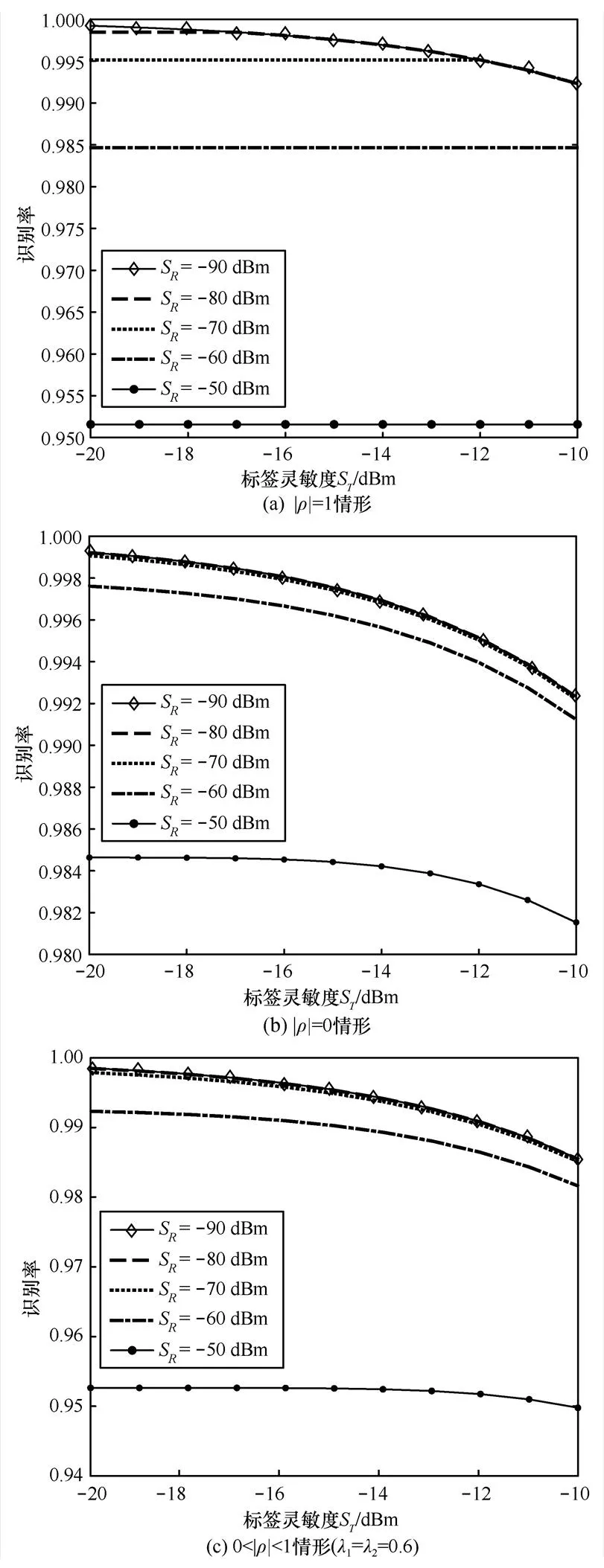
圖2 靈敏度對識別率的影響

圖3 相關系數λ對識別率的影響

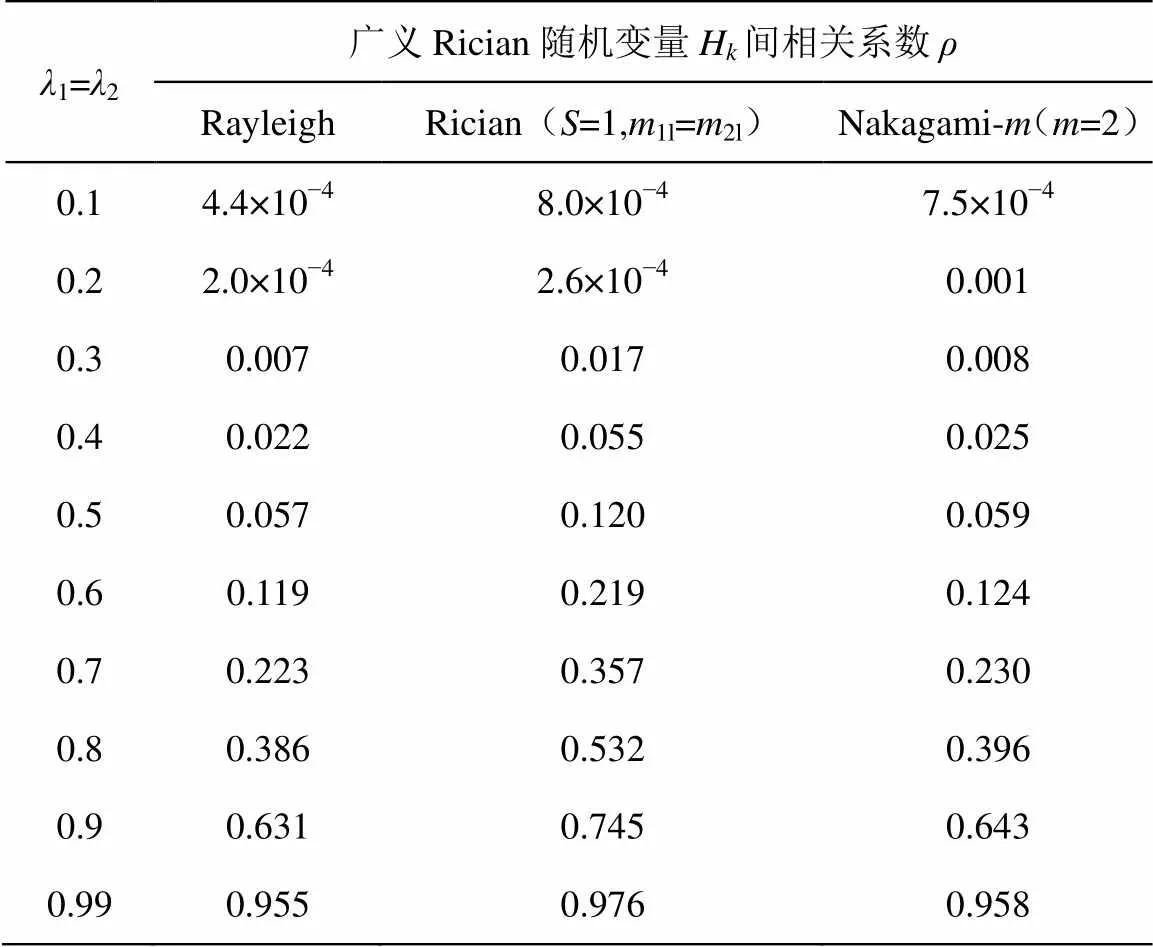
表2 參數λ與相關系數ρ的對應關系

6 結束語

本文基于廣義萊斯信道模型，給出了UHF RFID系統3種相關情形下識別率的顯示計算式，并且該計算式還能統一表示萊斯（Rician）、瑞麗（Rayleigh）和Nakagami-這3種信道下的識別率。實驗結果表明，Rician信道因為具有視距功率，其識別率優于Rayleigh信道，而對于Nakagami-信道，只需要=2就具有較Rician信道更好的識別率，故建議采用多天線分集的方式提高標簽識別率。而標簽識別率是由閱讀器和標簽的靈敏度共同決定的，且隨著閱讀器靈敏度的降低而加速惡化。對于Rayleigh和Nakagami-信道，信道相關系數對識別率的影響不大，而對于Rician信道的影響較為明顯。

[1] 李程, 錢松榮. 射頻識別動態定位方法[J]. 通信學報, 2013, 34(4): 144-148.

LI C, QIAN S R. RFID dynamic positioning method[J]. Journal on Communications, 2013,34(4):144-148.

[2] KIM D, INGRAM M A, SMITH W W. Measurements of small-scale fading and path loss for long range RF tags[J]. IEEE Transactions on Antennas and Propagation, 2003,51(8):1740-1749.

[3] LAZARO A, GIRBAU D, SALINAS D. Radio link budgets for UHF RFID on multipath environments[J]. IEEE Transactions on Antennas and Propagation, 2009,57(4):1241-1251.

[4] 佘開,何怡剛,李兵. 無源超高頻RFID系統鏈路預算分析[J]. 儀器儀表學報,2010,31(5):974-979.

SHE K, HE Y G, LI B. Passive UHF RFID budget analysis[J]. Chinese Journal of Scientific Instrument, 2010,31(5):974-979.

[5] 佐磊, 何怡剛, 李兵. 無源超高頻射頻識別系統路徑損耗研究[J]. 物理學報, 2013,62(14): 1-8.

ZUO L, HE Y G, LI B. Analysis and measurement of path loss effects for ultra high frequency radio-frequency identification in real environments[J]. Acta Physica Sinica, 2013,62(14):1-8.

[6] KIM D Y, JO H S, YOON H. Reverse-link interrogation range of a UHF MIMO-RFID system in Nakagami-fading channels[J]. IEEE Transactions on Industrial Electronics, 2010,57(4):1468-1477.

[7] BEKKALI A, ZOU S, KADRI A. Performance analysis of passive UHF RFID systems under cascaded fading channels and interference effects[J]. IEEE Transactions on Wireless Communications, 2015, 14(3): 1421-1433.

[8] CHAU Y A. Outage performance of RFID systems with multiple reader antennas over correlated forward and backscatter fading channels[C]//IEEE 21st Annual Wireless and Optical Communications Conference (WOCC). 2012:81-82.

[9] SMIETANKA G, GOTZE J. Modeling and simulation of MISO diversity for UHF RFID communication[C]// Computer Science and Information Systems. 2012:813-820.

[10] HE C, WANG Z J. Impact of the correlation between forward and backscatter channels on RFID system performance[C]//IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). 2011:3540-3543.

[11] SILVA C R N, LEONRDO E J, YACOUB M D. Product of two envelopes taken from-,-, and-distributions [J]. IEEE Transactions on Communications, 2018,66(3):1284-1295.

[12] GAO Y, CHEN Y, BEKKALI A. Performance of passive UHF RFID in cascaded correlated generalized Rician fading [J]. IEEE Communications Letters, 2016, 20(4):660-663.

[13] BEAULIEU N C, HEMACHANDRA K T. Novel simple representations for gaussian class multivariate distributions with generalized correlation[J]. IEEE Transactions on Information Theory, 2011, 57(12): 8072-8083.

[14] ZWILLINGER D. Table of integrals, series, and products (Eighth Edition)[M]. Elsevier, 2014.

[15] ERMOLOVA N Y, TIRKKONEN O. Laplace transform of product of generalized Marcum Q, Bessel I, and power functions with applications[J]. IEEE Transactions on Signal Processing, 2014, 62(11): 2938-2944.

Research on the identification performance of UHF RFID system considering the correlation of cascaded channel

SHE Kai1, HE Yigang2, LI Bing2, ZHU Yanqing3

1. School of Physics and Electronic Science, Hunan University of Science and Technology, Xiangtan 411201, China 2. School of Electrical Enginering, Wuhan University, Wuhan 430072,China 3. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China

The identification rate of UHF RFID system was restricted by multipath propagation effects. The system identification performance was studied considering the correlation coefficient between forward and reverse channels. Based on the generalized Rician fading channel model, the analytical expression of identification rate was derived under independent, full correlation and correlation cases. Compared with the existing analysis, the proposed uniform calculation formula of identification rate was for any correlation coefficient and kinds of channel conditions. The numerical computation and Monte-carlo simulations show that the influences of different correlation coefficients, channel conditions, sensitivity and distance on the identification rate.

RFID technology, identification rate, relevant channel, generalized Rician fading model

2017?12?25；

2018?06?20

TN925.93

A

10.11959/j.issn.1000?436x.2018123

佘開，shekai@126.com

國家自然科學基金資助項目（No.51637004, No.51777050）；國家重點研發計劃基金資助項目（No.2016YFF0102200）；湖南省自然科學基金資助項目（No.2018JJ2127）；湖南省教育廳科研基金資助項目（No.16C0641）

The National Natural Science Foundation of China (No.51637004, No.51777050), The National Key Research and Development Program of China (No.2016YFF0102200), The Natural Science Foundation of Hunan Province (No.2018JJ2127), The Research Foundation of Hunan Education Department (No.16C0641)

佘開（1980?），男，湖南長沙人，博士，湖南科技大學講師，主要研究方向為射頻識別的空口技術。

何怡剛（1966?），男，湖南邵陽人，博士，武漢大學教授、博士生導師，主要研究方向為測試與診斷、智能信息處理等。

李兵（1973?），男，湖南邵陽人，博士，武漢大學副教授，主要研究方向為射頻識別測試技術、智能電網技術等。

朱彥卿（1978?），男，湖南株洲人，博士，湖南大學助理教授，主要研究方向為射頻測試技術。