壓電疊堆式能量收集系統(tǒng)輸出特性研究
張 愷,王德石,周德鑫
(1.海軍工程大學(xué)兵器工程系,湖北 武漢 430033,2.海軍裝備部,北京 100841)
壓電疊堆式能量收集系統(tǒng)輸出特性研究
張 愷1,王德石1,周德鑫2
(1.海軍工程大學(xué)兵器工程系,湖北 武漢 430033,2.海軍裝備部,北京 100841)
研究了壓電疊堆式能量收集裝置的系統(tǒng)輸出特性,考慮整流電路的作用,建立了壓電結(jié)構(gòu)的機電耦合動力學(xué)模型,獲得了系統(tǒng)的輸出電壓和輸出功率的一般形式。利用該模型分析了壓電材料、激振頻率、激振力幅值和負載電阻對系統(tǒng)輸出性能的影響。結(jié)果表明,PZT-8壓電材料較PZT-5A和PZT-4有著更好的系統(tǒng)輸出特性;系統(tǒng)參數(shù)在和激振頻率、激振力幅值、負載電阻等完全匹配時,輸出性能最佳。
壓電疊堆;能量收集;機電耦合;輸出電壓;輸出功率
各種微功耗電子系統(tǒng)對電源的體積、壽命和能量密度等要求越來越嚴格,傳統(tǒng)的電池已不能滿足其能量供給需求。因此,研發(fā)新型的供電方式已成為解決這些電子器件發(fā)展瓶頸的迫切問題。振動能作為自然界中普遍存在的綠色能源,將其轉(zhuǎn)化為電能,有望解決微電子器件能源長期、持續(xù)供應(yīng)的要求。由壓電材料制成的能量收集裝置因具有結(jié)構(gòu)簡單、輸出電壓高、能量密度大等優(yōu)點而備受關(guān)注。
壓電式能量收集裝置是利用壓電材料的正壓電效應(yīng)來實現(xiàn)機械能向電能的轉(zhuǎn)換,轉(zhuǎn)換后的電能經(jīng)整流、穩(wěn)壓、存儲等環(huán)節(jié)為終端電路供電。壓電材料可按多種構(gòu)成形式應(yīng)用于壓電能量收集裝置中,通過改變壓電材料屬性、改變壓電單元工作模式、改變壓電振子的結(jié)構(gòu)形式等壓電材料構(gòu)成形式,可提高壓電式能量收集裝置的輸出性能。d33模式和d31模式是壓電材料目前兩種常用的工作模式,d33模式為作用力的方向與極化方向相同,d31模式為作用力與極化方向垂直。Baker等[1]通過將等體積的d33模式下的壓電晶堆與d31模式下的壓電懸臂梁進行對比實驗,結(jié)果表明晶堆的機電耦合系數(shù)要高于懸臂梁式的耦合系數(shù),相同應(yīng)力作用下,懸臂梁產(chǎn)生的能量要高于壓電晶堆產(chǎn)生的能量,其主要原因在于壓電晶堆的機械剛度大,從而使壓電單元產(chǎn)生的形變小。Roundy給出了類似的結(jié)論[2-3],同時,與d33模式相比,d31工作模式下的壓電能量收集裝置的諧振頻率更低。Yang等[4]研究了d33模式下的壓電盤的機電耦合系數(shù)與介電常數(shù)關(guān)系,結(jié)果表明兩者成正比關(guān)系。Richards等[5]建立了壓電能量收集裝置的機電耦合系數(shù)、機械品質(zhì)因數(shù)和轉(zhuǎn)換效率之間的數(shù)學(xué)模型,研究表明,適中的機電耦合系數(shù)和大的品質(zhì)因數(shù)可提高能量收集系統(tǒng)的效率。
為了有效預(yù)測壓電式能量收集裝置的能量輸出特性,本文通過聯(lián)立壓電方程和單自由度系統(tǒng)振動方程,獲得d33工作模式下的壓電結(jié)構(gòu)機電耦合動力學(xué)模型,利用該模型分析了壓電材料、負載電阻、激振信號頻率等對系統(tǒng)能量輸出性能的影響,研究結(jié)果可為壓電式能量收集裝置的設(shè)計優(yōu)化提供理論依據(jù)。
1 系統(tǒng)分析模型
將發(fā)電裝置等效為由壓電晶堆和彈簧、質(zhì)量、系統(tǒng)阻尼組成的機電耦合系統(tǒng),如圖1所示。圖中,V(t)和I(t)為壓電晶堆產(chǎn)生的電壓和電流;M、c、Ks分別為質(zhì)量塊質(zhì)量、系統(tǒng)阻尼、壓電晶堆的等效剛度;F為激振力;u為質(zhì)量塊的振動位移。
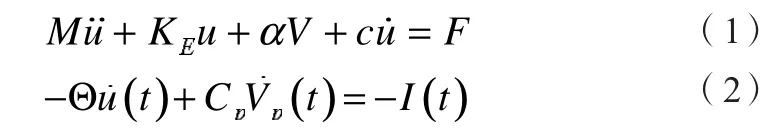


2 仿真分析
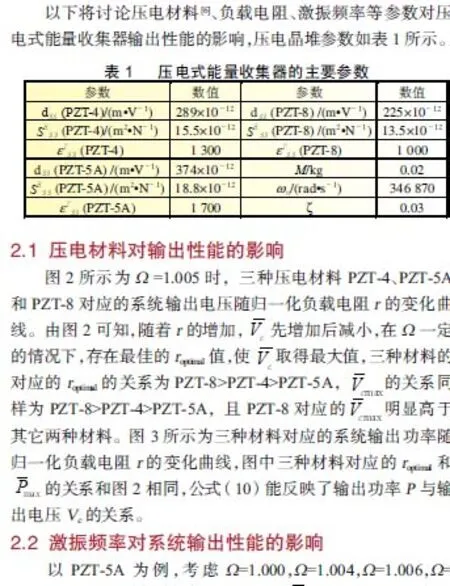
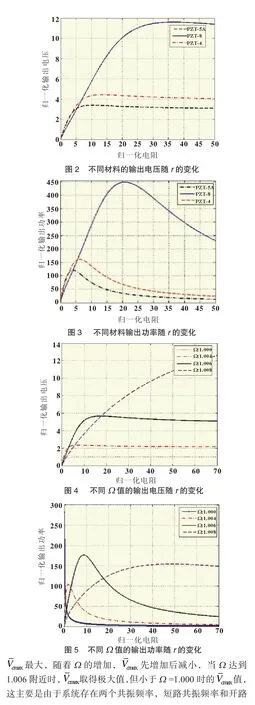

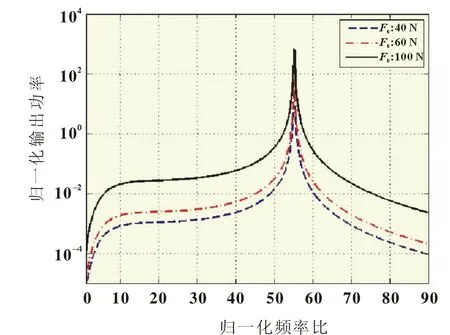
圖9 不同激振力對應(yīng)的P隨r的變化
壓電材料的受壓能力,防止其在工作時出現(xiàn)損壞。
3 結(jié)果與討論
本文利用壓電晶堆結(jié)構(gòu)的機電耦合動力學(xué)模型,分析了壓電材料、歸一化負載電阻r、頻率比Ω對能量收集系統(tǒng)輸出電壓和輸出功率等性能的影響,獲得了如下結(jié)論:
(1)壓電材料屬性對系統(tǒng)輸出性能影響較大,對比的三種壓電材料中,PZT-8壓電材料對應(yīng)的系統(tǒng)輸出性能更佳。
(2)激振力幅值越大,系統(tǒng)輸出功率越大,頻率比Ω=1左右時,輸出電壓和輸出功率達到最大,此時激振力頻率與系統(tǒng)共振頻率一致。
(3)在給定的系統(tǒng)中,存在最佳的負載阻抗使得系統(tǒng)輸出性能達到最佳。
[1] BAKER J,ROUNDY S,WRIGHT P.Alternative geometries for increasing power density in vibration energy scavenging forwireless sensor networks[C]//Proceedings of 3rd Int Energy Conversion Engineering Conf.San Francisco:3rd Int Energy Conversion Engineering,2005:959-970.
[2] ROUNDY S.On the effectiveness of vibration-based energy harvesting[J].Journal of intelligent Material Systems and Structures, 2005,16:809-823.
[3] ROUNDY S,LELAND E S.Improving power output for vibrationbased energy scanvengers[J].IEEE Pervasive Computing,2005(4): 28-36.
[4] YANG J,ZHOU H,HU Y,et al.Performance of a piezoelectric harvester in thickness stretch mode of a plate[J].IEEE Trans Ultrason Ferroelectr Freq Control,2005(52):1872-1878.
[5]RICHARDSCD,ANDERSON M J,BAHRD F,etal.Efficiency of energy conversion for devices containing a piezoelectric component [J].M icromech M icro,2004,14:717-721.
[6] 張福學(xué),王麗坤,王淵旭,等.現(xiàn)代壓電學(xué)[M].中冊.北京:科學(xué)出版社,2002:140-146.
Outputperformance of piezoelectric stacked energy harvester
ZHANG Kai1,WANG De-shi1,ZHOU De-xin2
(1.Department of Weaponry Engineering,NavalUniversity of Engineering,Wuhan Hubei430033,China; 2.The PLA Navy EquipmentDepartment,Beijing 100841,China)
The output performance of piezoelectric stack energy harvester was studied,the energy harvester was connected to an AC-DC rectifier,and the electromechanical coupling dynamic model was proposed.The expression of the normalized output voltage and output power was established.The effects on the output power performance of piezoelectric stack physical parameters,such as piezoelectric material parameters,the amplitude and frequency of the exciting force,the load resistance of the system were analyzed. The results show that PZT-8 has a better performance compared with PZT-4 and PZT-5A,when the amplitude and frequency of the exciting force and load resistance is according with the system parameters,the optimal performance can be obtained.
piezoelectric stack;energy harvesting;electromechanical coupling;output voltage;output power
TM 461
A
1002-087 X(2013)11-2028-04
2013-04-05
國家自然科學(xué)基金青年科學(xué)基金資助項目(51005241)
張愷(1985—),男,河南省人,博士,主要研究方向為壓電傳感器設(shè)計。

