小樣本厚尾觀測數據的信度加權混合分布擬合研究

郭建平，曹 杰，趙立龍

（南京信息工程大學a.經濟管理學院；b.物理與光電工程學院，南京 210044）

0 引言

抽樣分布研究是統計分析領域的重要課題，相對于大量觀測形成的大樣本數據的分布擬合問題，由少量觀測形成的小樣本數據的分布擬合問題存在更多不確定性，產生這種分布擬合不確定性的原因主要是因為遍歷的觀測較少，經驗分布所反映的特征與相關理論分布的特征相比較不明顯。信息反映相對不足使得研究者難以確定與之相互匹配的理論概率分布類型，建立在理論概率分布模型下的各種統計推斷結果的可靠性自然值得質疑。因此，準確判斷與樣本數據相匹配的理論分布類型對于研究隨機現象具有重要意義，只有確定理論分布類型，才能運用統計分析方法估計理論分布中的未知參數，得到理論分布模型的解析表達式，即分布密度或者分布函數，從而計算隨機變量的數字特征，完成統計推斷等一系列分析過程。

本文研究了具有厚尾特征的小樣本數據的分布擬合問題，獲得一組小樣本厚尾觀測數據后，通過觀察數據的分布形態，尤其是尾部特征，結合對數據分布的初步分析，可以選用一些常用理論概率分布模型來擬合。然而，統計實踐中經常發現單個連續概率分布模型對厚尾特征數據的擬合效果不盡如人意，對數據尾部的擬合常常出現高估或者低估問題，因此，有必要在這些單一概率分布模型的基礎上建立混合分布模型來擬合厚尾小樣本數據。混合分布模型的本質特征就是通過單一理論分布模型之間的相互修正，盡可能地匹配實際數據生成過程。如何通過權重的設置將兩個及其以上單一分布模型以加權形式“混合”在一起構成混合分布模型是此類研究的重要內容，在非壽險精算領域，這一混合比例被稱為結構參數，通常在擬合分布分析中，這個參數是未知的。本文則考慮樣本數據的均值和方差以及觀測數信息，借鑒保險精算學中的信度理論，通過信度因子計算混合分布模型權重值，即混合比例或者結構參數，在降低混合分布模型待估參數維數便利模型估計之余，賦予權重更實際的樣本信息。

1 文獻回顧與述評

統計實踐中存在著大量尖峰或厚尾或偏態的觀測數據，這些樣本數據顯著背離正態分布，如果用以正態分布為核心的傳統統計方法來分析，其結果往往令人難以置信。因此，建立能夠處理此類數據的新概率分布及相關的統計推斷新方法擬合非正態數據在統計學研究領域已經成為眾多學者關注的重要內容之一。

考慮兩個單一概率分布通過加權構成的混合模型：f(x)=pf1(x)+(1-p)f2(x)，其中 0≤p≤1，f1(x)和f2(x)為不同的單一分布密度函數，p為混合比例。不同的研究者對由兩個或以上分布形成的分布模型冠以不同稱呼，如疊加分布、混合分布、組合分布等，為了敘述簡潔，這里統一稱之為混合分布模型（以下簡稱混合模型）。大量的文獻對這種形式的混合模型進行了分析和實證研究。

王新軍和邵學清（2005）[1]提出了混合模型并給出分布參數的估計方法，實證分析結果表明混合模型的擬合效果顯著優于單一分布模型的擬合效果；趙桂芹等（2006）[2]對保險實務中具有“雙峰”或“多峰”特征的損失數據，提出了由帕累托分布與廣義帕累托分布組成的混合模型進行擬合的思想，但是對顯著影響擬合效果的閾值參數的選取問題沒有分析。田榮潔等（2014）[3]則通過分段擬合的方法提高了損失分布的擬合準確性。但是，如何分段缺乏數理基礎。陳倩(2015)[4]通過假設損失頻率服從泊松-伽瑪分布，研究了小樣本貝葉斯推斷的MCMC參數估計的優勢，較好地解決了由于損失數據不足給損失分布擬合帶來的難題。

上述研究豐富了數據分布的擬合問題，為進一步探索小樣本厚尾數據的分布形式奠定了堅實的基礎。通過梳理混合模型的研究文獻，發現如何匹配混合模型中單一分布的權重參數并沒有取得統一的認識，大量研究獲得包括權重參數在內的待估參數的方法主要是利用數值優化技術。通過數值優化技術獲得的權重參數實際意義不明確，同時增加一個未知參數也增加了估計的難度。

國外學者對權重配置問題也有論述，如McCulloch和Jr(2013)[5]使用拉格朗日乘數方法擴展了尖峰厚尾數據的擬合優度檢驗問題。Min等(2014)[6]提出了一個線性混合模型均值結構的擬合檢驗方法。Amin等(2015)[7]將離群點出現的概率值作為混合模型權重，使用混合模型擬合了含有離群點的樣本數據。

綜合國內外對混合模型的研究成果可以發現混合模型在工程技術或者社會科學研究領域都被廣泛應用。通過加權或者混合比例的方法對若干單一分布模型進行“混合”作為構建混合模型的主要方法已經被研究者普遍認同，由于分布之間的相互修正帶來的總體擬合效果的提高也被廣大研究者認識。但是，對于加權或者混合比例的確定尚無一致看法，對混合模型參數的估計方法也眾說紛紜，由于參數估計方法的差異致使模型迥異，間接導致了統計分析結果的不確定，影響了模型的應用和推廣。

本文試圖利用信度理論的思想確定混合權重。信度理論是研究如何正確、合理地處理先驗信息和后驗信息，即研究如何通過加權把兩者綜合起來的理論。信度理論萌芽于20世紀20年代，最早的信度理論被意外險精算師應用于計算勞工賠償險費率。通過數據樣本的期望和方差等信息的提取，獲得信度因子，把信度因子作為單一分布的權重參數擬合混合模型，通過充分利用樣本數據的各類型信息，更加準確匹配實際損失數據的發生規律。這種信度權重設置思想的主要優勢在于小樣本情況下通過融合統計研究問題的先驗信息，更有助于提高統計推斷精確程度。

2 建模過程

2.1 單一概率分布判別

單一概率分布是構成混合模型的基礎，獲得一組觀測數據之后，需要確定數據樣本適用的單一分布形式。確定一批數據適用某種概率分布的主要步驟是：首先根據觀測得到的數據樣本編制經驗分布并繪制經驗分布圖，然后，根據經驗分布圖的形態特點選擇與之最相似的理論分布族；最后，對選定的理論概率分布參數進行參數估計，確定與實際數據相互匹配的理論概率分布。

對于具有顯著厚尾特征的數據類型，需要使用平均剩余期望函數對尾部進行細致考察。平均剩余期望函數通常被定義為：eX(d)=E[ ]X-d|X＞d，其中X表示觀測隨機變量，d表示指定常數。如果平均剩余期望函數隨d遞增，在變量取值較大處的期望結果會很大，概率向右移，則表明變量X的尾部相比那些平均剩余期望函數遞減或增速較慢的分布的尾部更厚。反之，如果平均剩余期望函數隨著d遞減，說明變量X為輕尾分布。

實際分析過程中，可以通過繪制頻率密度直方圖并匹配相應的擬合分布曲線進行判斷，也可以用P-P概率圖和Q-Q概率圖進行分析。P-P圖是根據變量的經驗分布與指定分布的累積分布函數之間的關系繪制的圖形，Q-Q圖是用樣本數據的經驗分位數與所指定分布的分位數之間的關系曲線來進行檢驗，兩者均可以直觀判斷樣本數據是否較好服從某一分布。

2.2 信度因子確定

信度理論是研究如何通過加權把先驗信息和個體觀測后驗信息綜合起來的理論。在保險產品費率厘定中，精算師往往需要參考被保險人在過去一段時間內的損失數據來預測其未來風險成本。由于經驗損失數據來自經驗期內發生的保險事故，這些數據本身包含有很大程度的隨機波動，僅僅依靠這些數據來估計將來的風險并不準確。經驗數據所反映的被保險人的風險水平與風險子集平均水平的差別中，如何確定由于隨機波動所引起的部分和由于被保險人的確優于或者劣于風險子集平均水平而引起的部分分別是多少，以及如何確定兩個部分之間的比重分配是此類研究的重要內容之一，信度理論為解決此類問題提供了一個重要工具。

假設X是隨機變量，x1,x2,…,xn是其觀測值，在非壽險精算中經常把X的數學期望E(X)=μ或者對將來損失的估計值作為厘定費率的依據。一般而言，總體均值μ是未知的，通過有限個觀測值n來推斷總體均值μ必定會產生誤差，但是隨著觀測值個數n的不斷增加，推斷產生的誤差可以越來越小，當觀測值個數n足夠大時，樣本均值與總體均值μ充分接近。設α和γ為預先給定的比較小的正數，若n滿足不等式（1）：

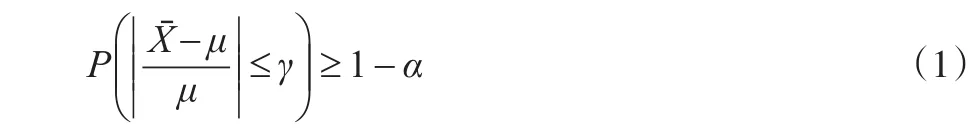
則稱n滿足完全可信性條件，取顯著性水平α=0.05，則不等式表示相對誤差不超過一個指定小的數γ的概率大于95%，并且根據不等式可得到滿足完全可信條件n的最小值。不等式（1）兩邊同乘以n，同除以標準差σ，同乘以μ，變形整理，可得式（2）：

設Zα2表示正態分布分位點，記，變形整理可得：，則n=，此即為用樣本均值X估計總體均值μ完全可信時的最小觀測數據量。

但是，保險實踐中實際觀測數據量很可能小于完全可信時的最小觀測數據量，為了使相對誤差標準不等式（1）仍成立，在式（1）中乘上了一個介于0～1之間的修正系數Z，Z被稱為信度因子，變形如下：

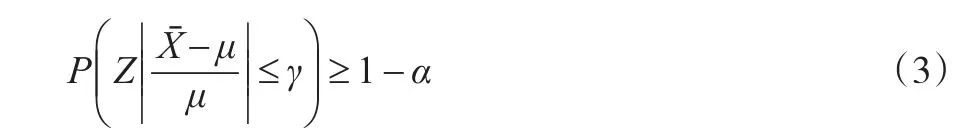
由于Z介于0～1之間，因此，式（3）可以成立。類上推導過程，可以得到信度因子Z的解析表達式：

這就是部分可信性理論的平方根法則，其中n0表示完全可信條件下的最小觀測數據量。由式（5）可知，如果給出了觀測值個數n，也就可以知道信度因子Z的值。綜合完全可信與部分可信兩種情況，將信度因子表示成

根據信度因子的推導過程和表達式可知，信度因子綜合了樣本期望和方差以及觀測個數的信息，借助于信度因子有利于更好地推測和判斷數據分布的相關特征。對于給定樣本數據，通過方差和期望的計算，容易獲得信度因子，如果把信度因子作為權重引入混合模型，理論上可以提高數據擬合精度。

2.3 參數估計

選擇了單一分布模型并計算出信度因子以后，可構造混合模型。

定義1：設X為隨機損失變量，f1(x)和f2(x)分別為單一連續分布的概率分布密度函數，Z為式（5）定義的信度因子，令f(x)=Z·f1(x)+(1-Z)·f2(x)，則稱f(x)為信度加權混合分布模型的概率密度函數。對于離散數據，這里的分布密度f(x)可以理解為分布函數即F(X)。

當前估計混合模型參數的方法主要是利用計算機進行數值迭代，通過滿足一定的收斂標準確定最優值。但是，不合適的迭代初始值常常使得迭代程序不收斂，因此，選擇一個相對準確的初值對于成功估計參數具有重要意義。極大似然估計作為一種精確的參數估計方法理應首先考慮，但是混合模型是一種加法模型，對數運算處理加法模型沒有優勢；矩估計也是常用的參數估計方法之一，其基本思想是求解參數使得樣本分布的各階原點矩等于理論分布的各階原點矩。除此之外，分位點估計法也是常用的參數估計方法之一，其基本思想是通過理論分布位點與實際樣本的分位點相匹配確定相應參數。權衡考慮三種方法的計算便捷程度和信息利用的充分程度，擬選擇矩估計法對參數進行估計。

使用矩估計法進行估計時需要計算理論分布的各階原點矩，為計算簡潔，可以通過構造矩母函數來生成各階矩，完成矩估計。混合模型的矩母函數為：

混合模型的矩母函數是單一分布矩母函數的信度加權和，通過矩母函數可以方便計算出理論分布各階原點矩。把通過觀測得到的損失數據x1,x2,…,xn視為損失隨機變量X的一個容量為n的樣本，則定義為樣本的k階原點矩。當k分別等于1，2，3，4時，得到樣本的一至四各階原點矩，令理論分布的各階原點矩分別等于相應的樣本經驗分布的各階原點矩，即可以求出混合模型的四個待估參數值。

2.4 擬合效果分析

對于得到的混合模型，通過實際值與各種分布擬合值靠近程度的比較可以判斷出擬合效果的優劣。針對某些特定分位點上的擬合情況，為了對厚尾數據的尾部性質進行細致的觀測，本文給出了95%以后尾部觀測分位點的擬合值。通過理論分析可以認為混合模型由于考慮了數據的期望和方差以及誤差精度之間的內在聯系，對數據的擬合效果理應優于單一分布的擬合效果。

3 實證

3.1 樣本數據說明

這里選擇我國1980—2015年間火災損失數據為樣本，用于比較混合模型和單一分布模型擬合厚尾樣本數據的優劣。原始火災造成的直接財產損失數據見后文表1，直接損失數據來自《中國火災統計年鑒》中國人事出版社（2012），通貨膨脹率數據來自國家統計局網站。

3.2 模型建立

3.2.1 描述性統計分析

以下主要使用SAS系統進行計算，樣本數據描述性統計分析結果如表1所示。

表1 描述性統計量

根據偏度系數為1.42285303可以判斷這批數據呈現高右偏態分布趨勢，由峰度系數2.14956349，小于正態分布的峰度系數3，可以判斷與正態分布相比數據尖峰特征不明顯。另外，通過上文介紹的經驗剩余函數，利用經驗剩余函數圖能判斷出數據具有厚尾特征，限于篇幅這里省略了相關分析過程。

根據對原始數據的初步分析可知樣本數據具有典型雙峰、厚尾且高偏態分布特征，這意味著常用的單一概率分布很難準確擬合這類數據，使用混合分布擬合這類樣本數據或許會有較好效果。綜合相關文獻的研究結果，本文擬采用對數正態分布和指數分布組成混合分布模型來擬合這批數據。對數正態分布中間部分相對較薄，尾部相對較厚，而指數分布中間較厚尾部漸薄，兩者結合，既可以形成中部的峰值特征又可以校正尾部的形狀。為了便于比較，本文同時給出單一分布的數據擬合效果。

3.2.2 單一分布的擬合優度檢驗

根據數據分布特征，給出了對數正態和指數分布兩條擬合曲線，檢驗統計量如表2所示。

表2 擬合優度檢驗

由表2可知對數正態分布所有三種擬合優度檢驗統計量及其概率值在顯著性水平為0.05時均顯著，故這批數據用對數正態分布擬合不適合；指數分布的K-S統計量在0.05的顯著性水平上不顯著，但另兩個統計量及其概率值在0.05的水平上則顯著，綜上認為這批數據用對數正態分布或指數分布單一的分布形式來擬合并不恰當。為便于和混合分布模型的擬合結果相互比較，給出了單一對數正態分布和指數分布的尾部部分分位數擬合值，如表3所示。

表3 單一分布分位數擬合值比較

共36個觀測值，在表3中，95%的百分比位于0.95×36=34.2位置處，即第34和第35個觀測值（31.78295和38.95464）之間的0.2位置處，取31.78295×0.8+38.95464×0.2=33.217288。其余各個分位點上的觀測值同樣計算。

估計的正態分布均值為μ=2.211418，標準差為σ=0.903628，對于95%的百分比，相應分位點為1.645，則(lnx-μ)/σ=1.645，可以求出對數正態分布的估計值為40.359。估計的指數分布exp(λ)的參數λ=12.77636，對于95%的百分比，有1-e-x/12.77636=0.95，可求出指數分布的估計值為40.359。其余分位點上的相應分布的估計值同樣計算。

3.2.3 信度因子的計算

根據上文所述，使用信度因子進行分布加權。假設顯著性水平α=0.05，指定小的數γ=0.1，則Zα2=1.645，λ0=，給定樣本數據的均值為12.7763643，方差為101.906967，完全可信條件下的最小觀測個數為：

由于數據量僅為36個，不滿足完全可信標準，計算信度因子如下：Z=0.23。

3.2.4 混合分布模型的確定

相對于指數分布而言，單一分布擬合時對數正態分布的三個統計量在更高的顯著水平上被拒絕，而指數分布的K-S檢驗統計量D在0.05的顯著水平上不能拒絕樣本數據來自指數分布的零假設，故先驗假定這批數據來自指數分布，構建的混合模型如下：

模型中的f1(x)和f2(x)分別為對數正態分布和指數分布的密度函數，含有三個待估計參數。

3.3 參數估計

將相應參數帶入混合模型，得到理論分布的一至三階各階原點矩解析式。

計算的樣本分布的一至四階各階原點矩如下：

令樣本分布的各階原點矩等于理論分布的各階原點矩，使用計算機數值計算方法得到三參數的值。為便于比較，單一分布的參數擬合結果也列于表4中。

表4 信度加權的混合模型的參數估計結果

最終信度加權的混合模型的分布密度函數：

3.4 擬合效果比較

為了比較混合模型對數據的擬合效果，令信度加權的混合分布密度函數分別等于相應的分位點概率值，得到分位點估計值如下頁表5所示。

表5中，混合模型分位數估計值的計算首先按照信度因子匹配相關概率，如95%，分解為95%×0.77=0.7315，95%×0.23=0.2185。然后計算0.7315對應的正態分布分位點為0.6174，令 lnx=2.6410+0.5212×0.6174，得到x值為19.352；令F(x)=0.2185，容易求出指數分布對應的x值為17.259，相加得到36.610。余下各個分位點的估計值同樣可以求出。由表5結果可知由于反映均值和方差信息的信度權重修正，混合模型的尾部擬合值更加接近觀測值。綜上分析，使用混合模型擬合損失數據具有較理想的擬合效果，相對于單一分布模型而言，使用混合模型對厚尾特征的損失數據進行擬合研究結果將更加可靠。

表5 混合模型擬合效果估計值

4 結論

本文使用混合概率分布模型對一類厚尾特色數據樣本的分布規律進行了擬合研究。不同于現有混合模型的擬合方法，本文借鑒了保險精算原理中信度理論的思想，通過信度因子為單一分布匹配了混合的權重，理論分析和實證結果均表明信度因子加權的混合模型顯著提高了厚尾數據的擬合精度。

能否準確擬合樣本數據的分布對于統計理論研究具有重要意義，運用統計分析方法估計理論分布中的未知參數，得到理論分布模型的解析表達式，即分布密度或者分布函數，計算隨機變量的數字特征，完成統計推斷并做出統計決策等一系列統計分析過程正確與否完全取決于對樣本分布的判斷與擬合。雖然現有概率分布能夠匹配實際統計實踐中的大量樣本數據分布問題，但是，統計現象的各種復雜多變性日益降低著這種匹配的精確度，使用混合概率分布模型來擬合各種“特色”樣本數據愈發有必要。在統計實踐領域，準確擬合數據分布不但有助于研究者深刻理解統計問題，而且也為研究者最終解決問題提供了思路。