磚混結構單體易損性預測方法研究

祁皚 劉梅婷 顏學淵

(福州大學土木工程學院 福建福州 350116)

0 引言

在編制福建省幾個城市的抗震防災規劃過程中發現，已有的群體震害特征類比預測方法預測的震害結果，與宏觀震害統計結果及傳統的經驗認識有明顯的差異。因此，有必要對群體震害特征類比預測方法進行一定的改進，使其更貼合實際并具備一定的可靠性。建立可靠的樣本庫是有效運用該方法的保證，可靠樣本庫的建立又需要有合理的單體易損性預測方法。磚混結構，不僅是目前我國城鎮里使用最廣，同時也是地震時人員傷亡最多的建筑結構類型之一。因此，本文分別利用簡化方法、PKPM建模分析方法和超越強度倍率法，對磚混結構進行震害預測，并將預測結果進行對比；針對簡化方法存在的不足之處，對其進行適當的改進；用改進的簡化方法，對4個框架結構工程實例進行震害預測，并將預測結果與PKPM建模分析方法和超越強度倍率法進行對比，驗證其可靠性。

1 3種單體易損性預測方法

1.1 防災規劃上的簡化方法

該方法選擇可表征結構破壞程度的震害指數作為預測結構震害的依據。表1給出了二者間對應關系。

表1 結構震害等級與震害指數的對應關系

馬東輝等提出了磚混結構的抗震性能簡化評價方法[1]。該方法采用樓層單位面積的平均抗剪強度作為磚結構房屋的抗震能力指標，用修正得到的震害指數作為其破壞指標。具體計算步驟如下：

(1)計算第S層樓的抗力RS。

式中，Fk為第s層樓第k片墻的斷面積(cm2)；

As為第s層樓的建筑面積(m2)；

α為樓層地震剪力折算系數，按式(2)進行計算；

Rτ為墻體抗剪強度( 10N/m2)，按式(3)進行計算。

式中，i為樓層序號；

s為計算樓層序號；

n為總樓層數。

Rτ=0.14(n-s+1)+0.014Rm+0.5

(3)

式中，Rm為砂漿標號；其它符號意義同式(2)。

(2)對歷史震害資料的分析表明，磚混結構某一樓層的震害指數Ds與它的抗力有下列關系：

6度 Ds(6)=1.864-0.007Rs7度 Ds(7)=1.977-0.006Rs7.5度 Ds(7.5)=1.9758-0.005Rs8度 Ds(8)=1.975-0.005Rs8.5度 Ds(8.5)=1.9096-0.0044Rs9度 Ds(9)=1.866-0.004Rs

(4)

(3)考慮到結構的抗震能力受其質量和設計標準等因素的影響較大，對Ds按式(5)進行適當的修正。

Dsm(I)=Ds(I)[1+∑Ci]

(5)

式中，Ci為抗力的修正系數，按表2確定；

Dsm(I)為修正后第s層樓的震害指數。

注：74、78規范對抗震墻的布置、高度限值、設防水準、樓梯間的布置、構造柱和圈梁的布置等有不同的規定，詳見相應規范。

由于式(5)的修正會受到負值和零值的影響，所以，當式(4)計算出來的結果為負值或零值時，在使用式(5)進行修正時，Dsm均取0.05計算。求出一幢樓各層樓的破壞等級以后，再根據薄弱層的破壞等級確定整幢樓的震害等級。

下文以該方法對莆田市涵江區某房屋進行震害預測。

該工程于2003年建造，設計使用年限為50年，未設防，設計地震分組為第三組，其他：采用現澆混凝土樓、屋面板，主要承重墻體為240 mm厚及180 mm厚實心磚墻。設有混凝土構造柱，樓、屋面板均設置圈梁，經過現場測試，砌筑砂漿為M1。其一、二層建筑平面圖如圖1～圖2所示。

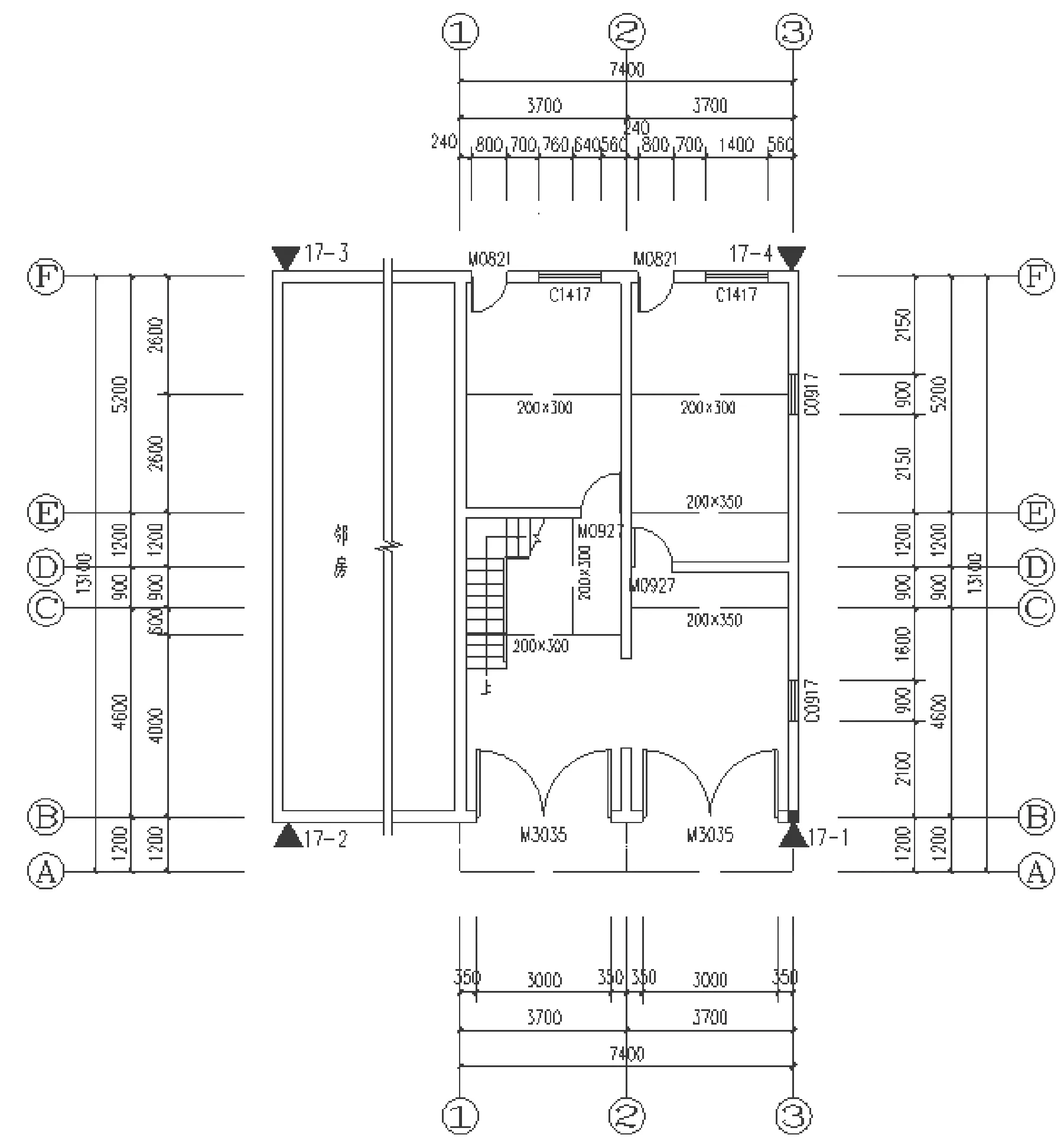
圖1 一層建筑平面圖

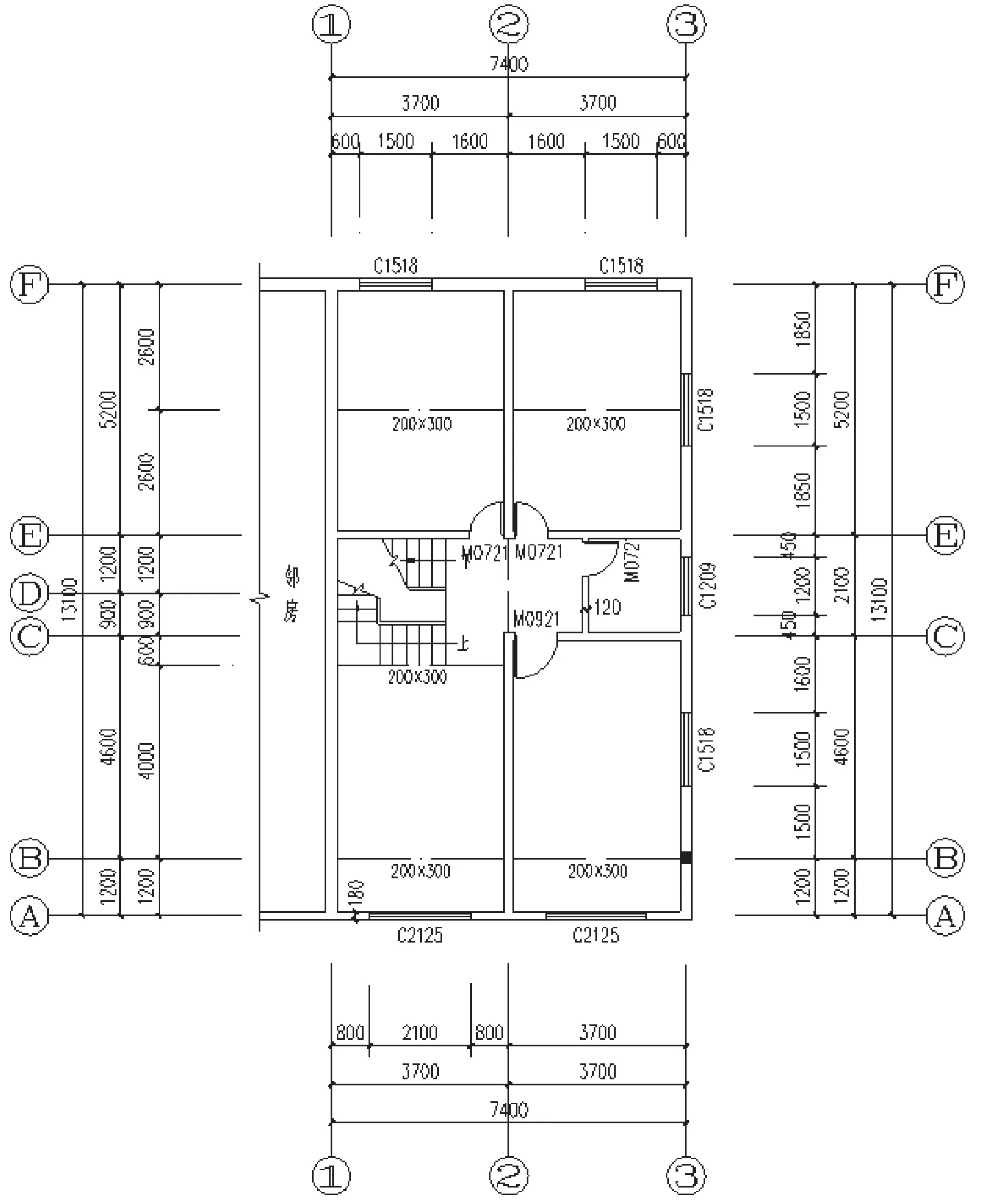
圖2 二層建筑平面圖

取薄弱層對應的震害指數，按表1震害等級與震害指數的對應關系進行判定，得到6～9度地震作用下結構的震害情況。為了方便對比，將結果列于表3第2列和第3列。

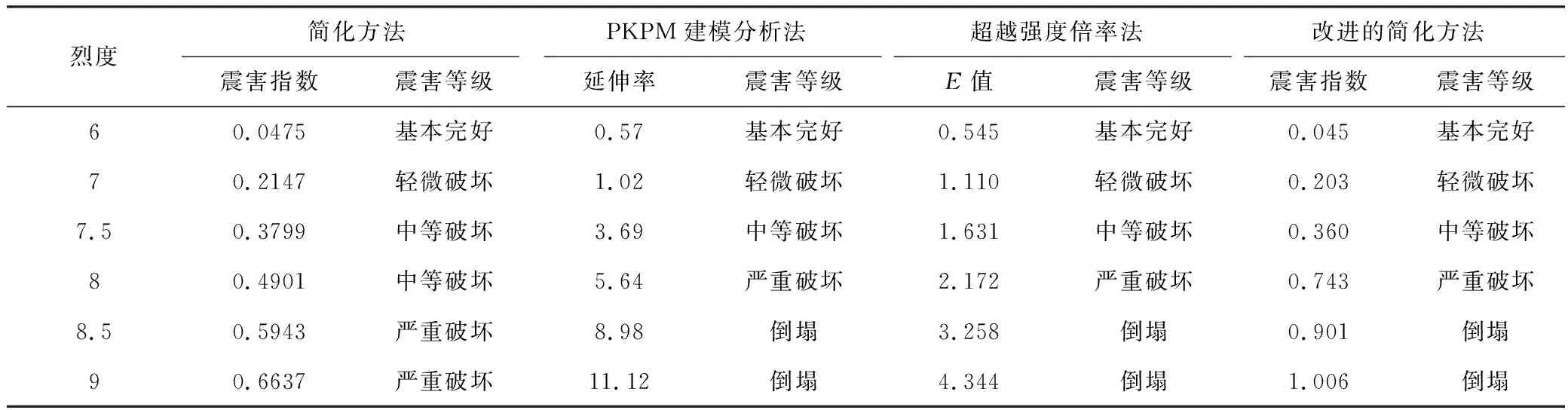
表3 結構采用不同單體震害預測方法得到的震害情況的對比

1.2 PKPM建模分析方法

該方法選擇可表征結構破壞程度的延伸率作為預測結構震害的依據。二者的對應關系如表4所示。李樹楨等[2]建立了一個單體磚混結構的易損性預測方法，該方法以層間延伸率作為破壞指標。該方法在臨汾市重要建筑的震害預測中，得到了令人滿意的結果。

表4 結構震害等級與延伸率的對應關系

本文采用PKPM中“砌體結構鑒定加固”模塊，計算樓層延伸率μ，再按表4確定結構的震害等級。具體計算步驟如下[3]：

(1)根據砌體各墻塊抗力與效應之比ζ(i)，按式(6)計算各樓層的抗力與效應之比ξ。

式中，n為墻體的塊數。

(2)取ξ值最小的樓層為結構薄弱層，并按式(7)計算樓層延伸率μ。

(3)考慮到建筑的抗震能力受其使用情況、施工質量等因素的影響較大，對式(7)計算得到的延伸率按式(8)進行修正。根據李樹楨等[2]的研究，修正系數Ci的取值見表5。最后，將修正后的延伸率μ按照表4判定結構的震害情況。

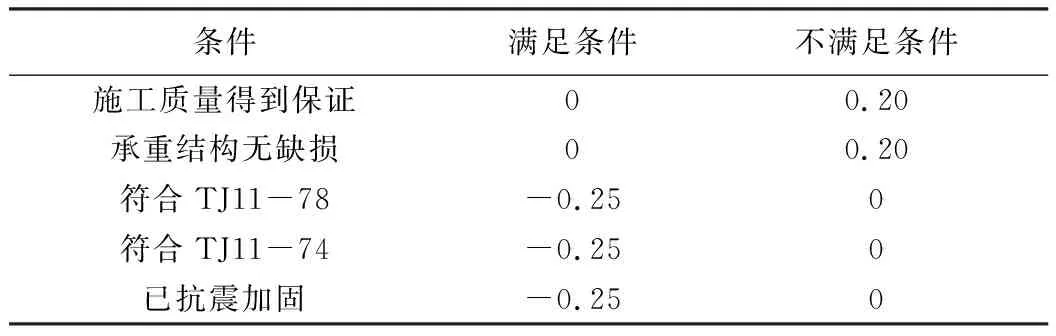
μ=(1+∑Ci)μmax (8)

注：74、78規范對抗震墻的布置、高度限值、設防水準、樓梯間的布置、構造柱和圈梁的布置等有不同規定，詳見規范。

現在，用該方法對前述磚混結構再進行震害預測。首先計算有關面積，如表6所示。該磚混結構的三維模型，如圖3所示。

表6 有關面積 m2

圖3 該房屋三維模型

查看各層計算結果，發現各烈度下都是首層的抗力與效應之比ξ最小，因此取首層的進行計算。6～9度地震作用下首層的抗震驗算結果如圖4～圖9所示。

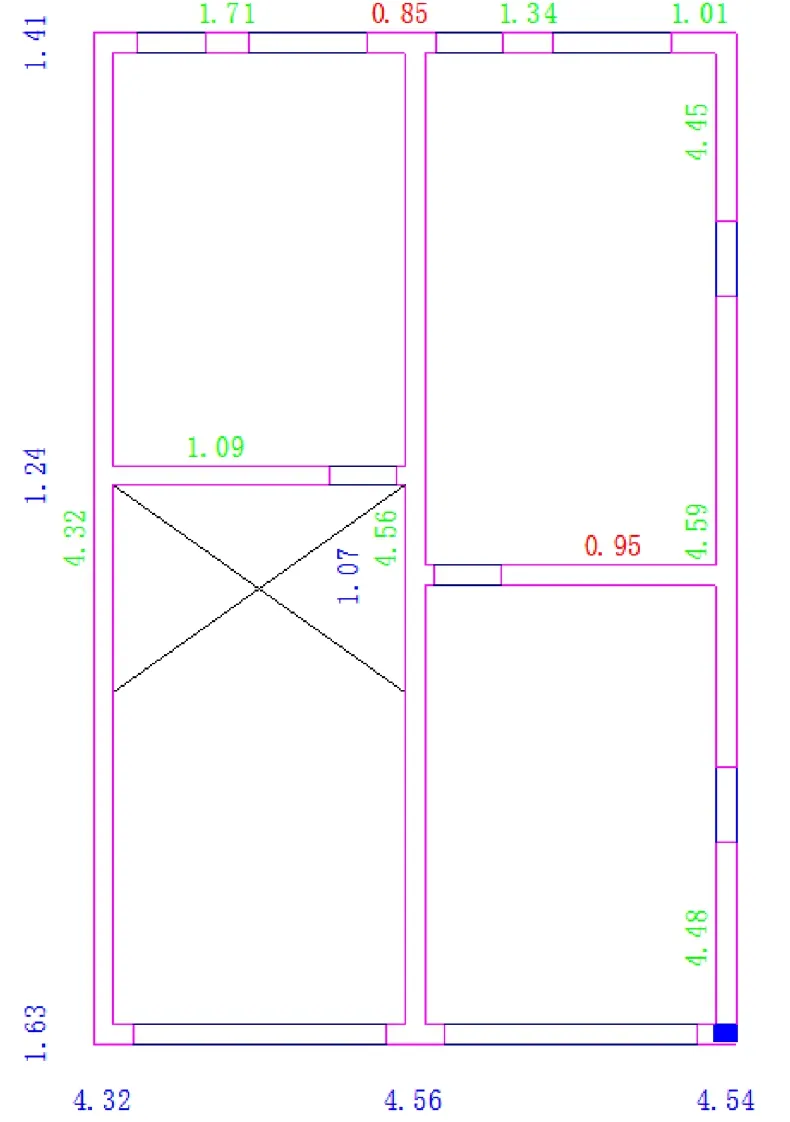
圖4 6度地震作用下首層的ξ(i)

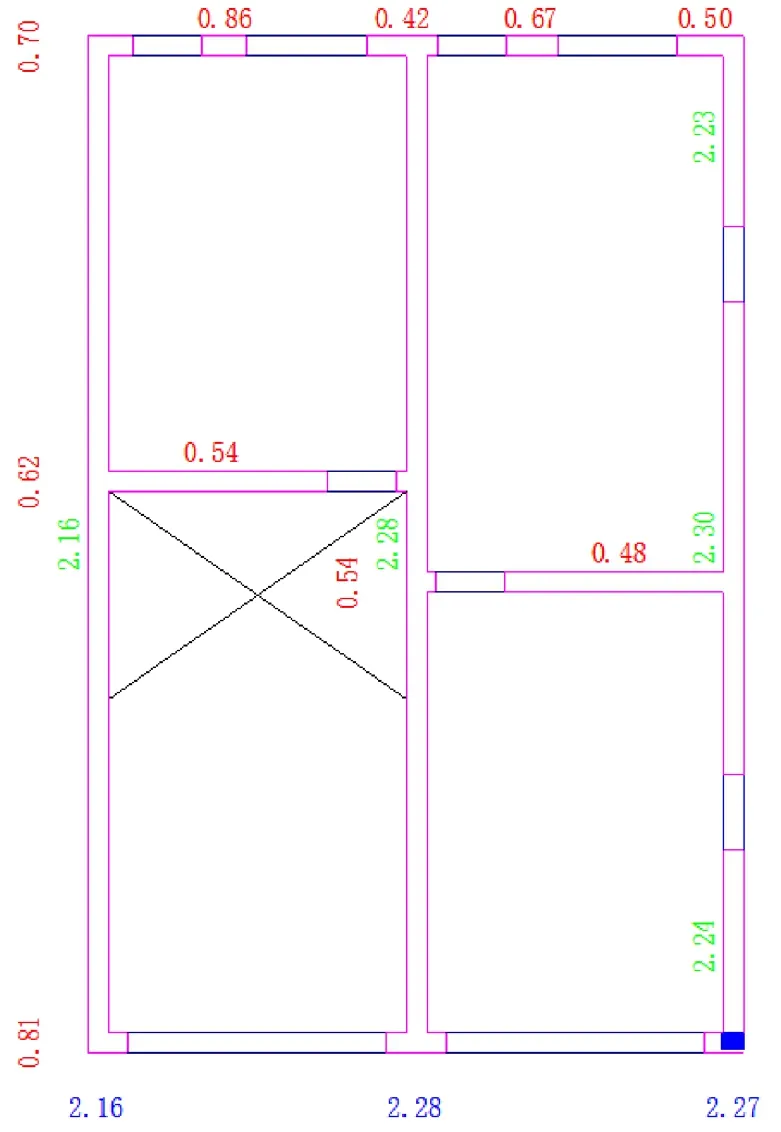
圖5 7度地震作用下首層的ξ(i)

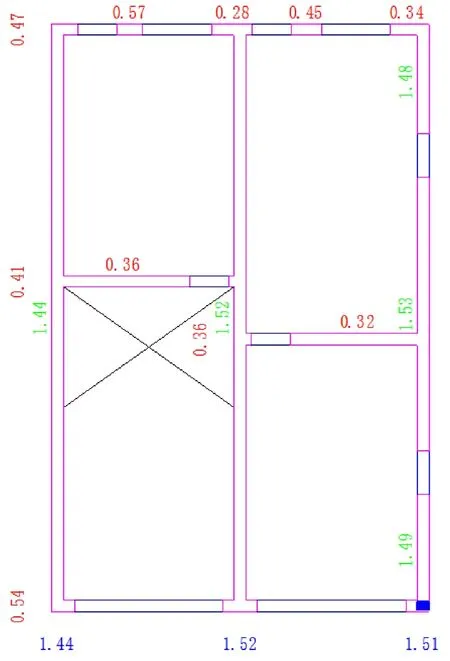
圖6 7.5度地震作用下首層的ξ(i)

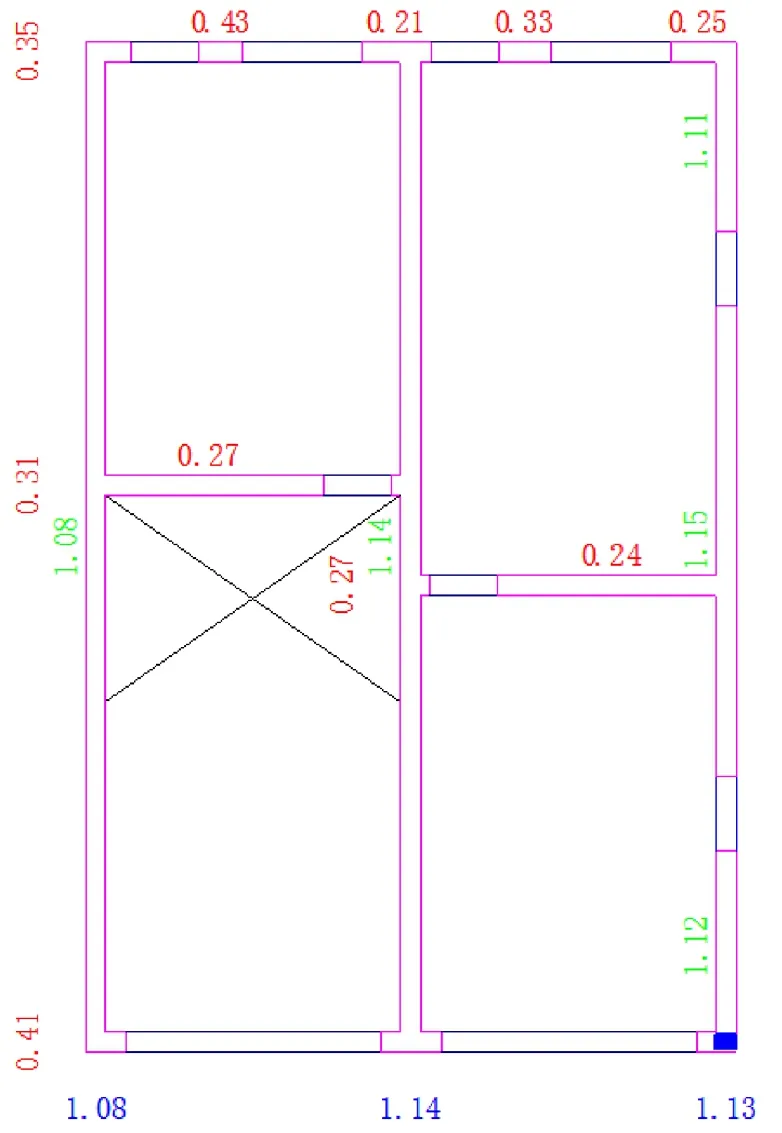
圖7 8度地震作用下首層的ξ(i)

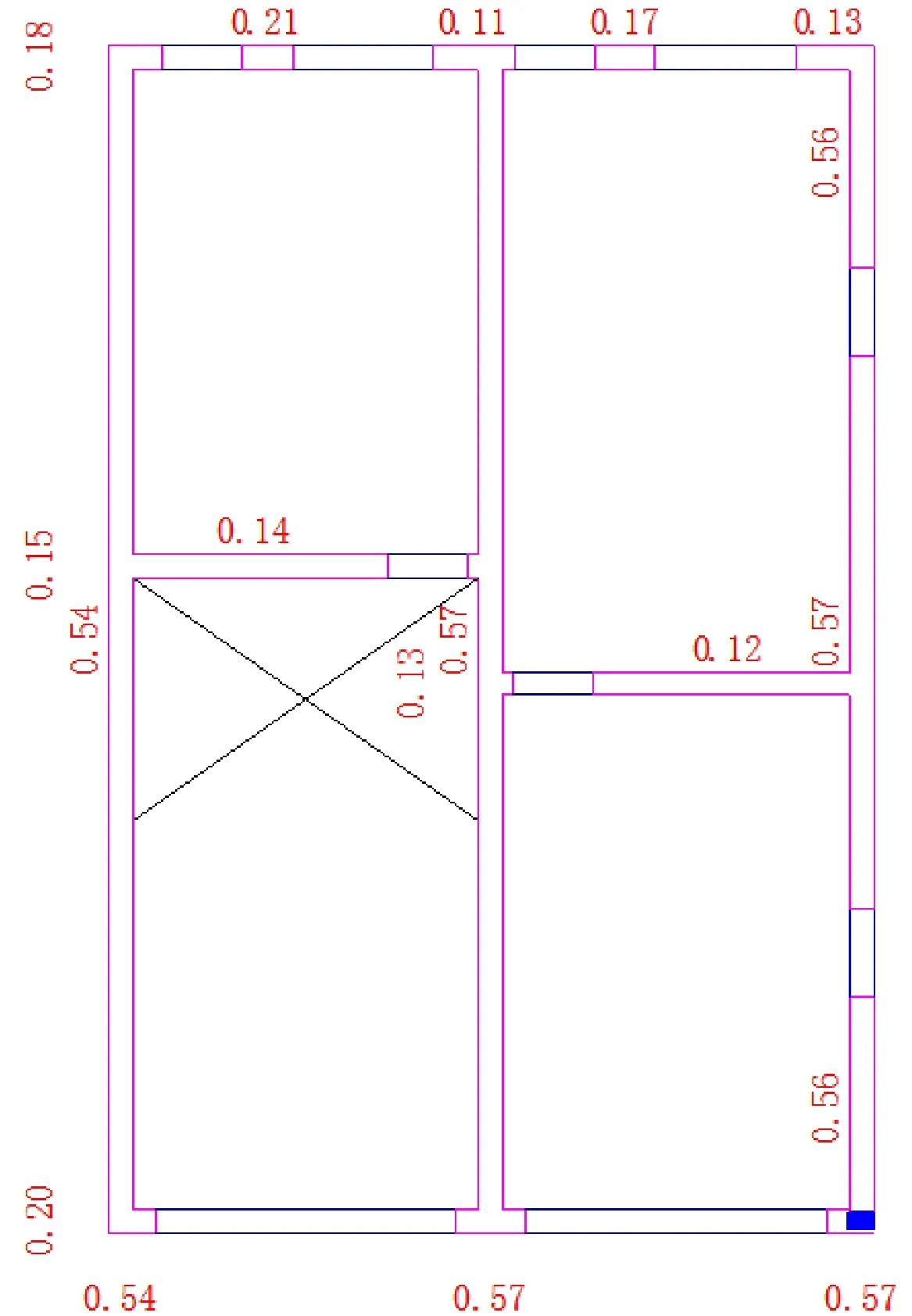
圖8 8.5度地震作用下首層的ξ(i)

圖9 9度地震作用下首層的ξ(i)

利用式(6)計算出各烈度下首層抗力與效應之比ξ，如表7所示。根據表7中的數據，先利用式(7)計算出各烈度下結構最大樓層延伸率μmax，并按式(8)進行修正后，最后按表4所示震害等級與延伸率的對應關系進行判定，得到各烈度下結構的震害情況，如表3第4列和第5列所示。

從表3中可以看出，在8度及以上地震作用時，與PKPM建模分析法相比，用防災規劃上的簡化方法的預測結果偏輕。為進一步證實防災規劃上的簡化方法對震害的預測偏輕，本文再采用超越強度倍率法對磚混結構進行易損性預測。

表7 各烈度下結構首層抗力與效應比ξ

1.3 超越強度倍率法

該方法選擇可表征結構破壞程度的超越強度倍率值(E值)作為預測結構震害的依據。用結構第s層的抗剪強度和地震剪力來確定結構第s層的超越強度倍率值(E值)[4]。通過對我國幾次大地震中無構造柱的多層磚混結構破壞狀態與抗力的對應關系的統計分析，可得出其震害等級與E值的對應關系如表8第2列所示[5]。

表8 磚砌體結構的震害等級與E值的對應關系

試驗結果還表明，與無構造柱的相比，設有構造柱的磚砌體的抗剪強度和變形能力均有明顯的提高。因此，震害統計也表明，設有構造柱的磚砌體房屋的震害等級與E值的對應關系如表8第3列所示[5]。

基于磚砌體結構的應用范圍和破壞特點，尹之潛等人[4]提出了用超越強度倍率法對結構單體進行易損性預測。用VS表示結構第S層的抗剪強度，QS表示地震剪力，則該樓層的破壞狀態可用以下公式的E值表述，最后根據計算出來的E值判定結構的震害等級。

E=QS/VS

(9)

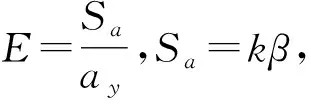
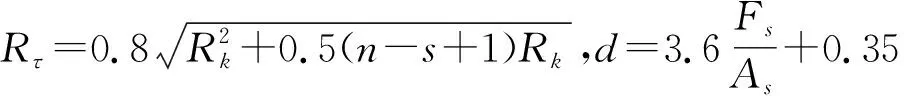
其中，Sa=kβ為地震加速度反應譜(g)，對于磚結構，可取kβ=Samax；

ay為樓層屈服加速度(g)；

Rs為第s層平均抗剪強度(N/cm2)；

Rτ為磚砌體標準抗剪強度(N/cm2)；

As為第s層的建筑面積(m2)；

Fs為第s層縱橫磚墻未扣除開孔的斷面面積總和(m2)；

d為樓層重力代表值修正系數，與Fs/As有關;

Ci為墻體抗剪強度修正系數，考慮設防標準、抗震措施等對磚砌體結構強度的影響，參照李樹楨等[2]的研究按表5取值；

n為房屋層數；

s為計算的樓層；

Rk為非抗震設計的磚砌體標準抗剪強度(N/cm2)。

現在用超越強度倍率法，對前述磚混結構再進行易損性預測。按式(9)分別計算出在6-9度地震作用下結構各樓層的E值，如表9所示。分別取表9所示6-9度地震作用下各樓層E值中的最大值，按表8第3列有構造柱的磚砌體結構的震害等級與E值的對應關系進行判定，得到6-9度地震作用下結構的震害情況。將結果列于表3的第6列和第7列。

由表3可以看到：在8度及以上地震作用時，結構采用超越強度倍率法進行預測得到的震害等級與PKPM建模分析法的預測結果一致。而且用防災規劃上的簡化方法對一個未設防的磚混民房進行預測，在9度罕遇地震作用下，預測出來的震害等級是"嚴重破壞"即此房屋還未倒塌，這與傳統的震害統計經驗有很大差距。所以，應該對防災規劃上的簡化方法進行一定的改進，使其預測結果接近于PKPM建模分析法和超越強度倍率法的預測結果。

表9 6～9度地震作用下各樓層的E值

2 簡化方法的改進

由表2可知，原修正系數沒有考慮89版以后的《抗震規范》。因而，考慮提高震害指數與抗力的關系式中8度及以上烈度所對應的參數，并增加89版《抗震規范》以后的修正系數。通過大量試算，并將試算結果與PKPM建模分析法和超越強度倍率法的預測結果進行對比，直到三者基本符合為止，由此給出了修正后的關系式和修正系數。

暫取磚結構某一樓層的震害指數與它的抗力的關系為式(10)所示。后面證明該公式正確。

6度Ds(6)=1.864-0.007Rs7度Ds(7)=1.977-0.006Rs7.5度Ds(7.5)=1.9758-0.005Rs8度Ds(8)=3.16-0.008Rs8.5度Ds(8.5)=3.0554-0.0070Rs9度Ds(9)=2.9856-0.0064Rs

(10)

式中，Rs為第s樓層的抗力值(kg/m2)，由式(1)求得。

考慮建筑整體設防水平的提高和規范的更新，對磚砌體結構的修正系數進行適當的修改，如表10所示。其他的要求與原簡化方法中的一樣。用改進的簡化方法對前述結構重新進行易損性預測，預測結果見表3第8列和第9列。從表3可看出，改進簡化方法預測的震害等級與超越強度倍率法和PKPM建模分析方法的預測結果比較一致。

注：a. 74、78、89三個規范在高度限值、最大高寬比、抗震縫布置、樓梯間布置、構造柱和圈梁布置等方面作了不同的規定，詳見相應規范；b. 括號里面的數字代表原來的修正系數；有下劃線的為本文的新增項。

3 其他工程實例加強驗證

實例1：莆田市涵江區白塘鎮鎮前村孝戶112號民房，該工程于2003年建造，設計使用年限為50年；未設防，設計地震分組為第三組；其他：采用現澆混凝土樓、屋面板，主要承重墻體為180 mm厚及240 mm厚實心磚墻。房屋四角均未設置混凝土構造柱，樓、屋面板均設置圈梁。經過現場測試，砌筑砂漿為M1。其一、二層建筑平面圖如圖10～圖11所示。

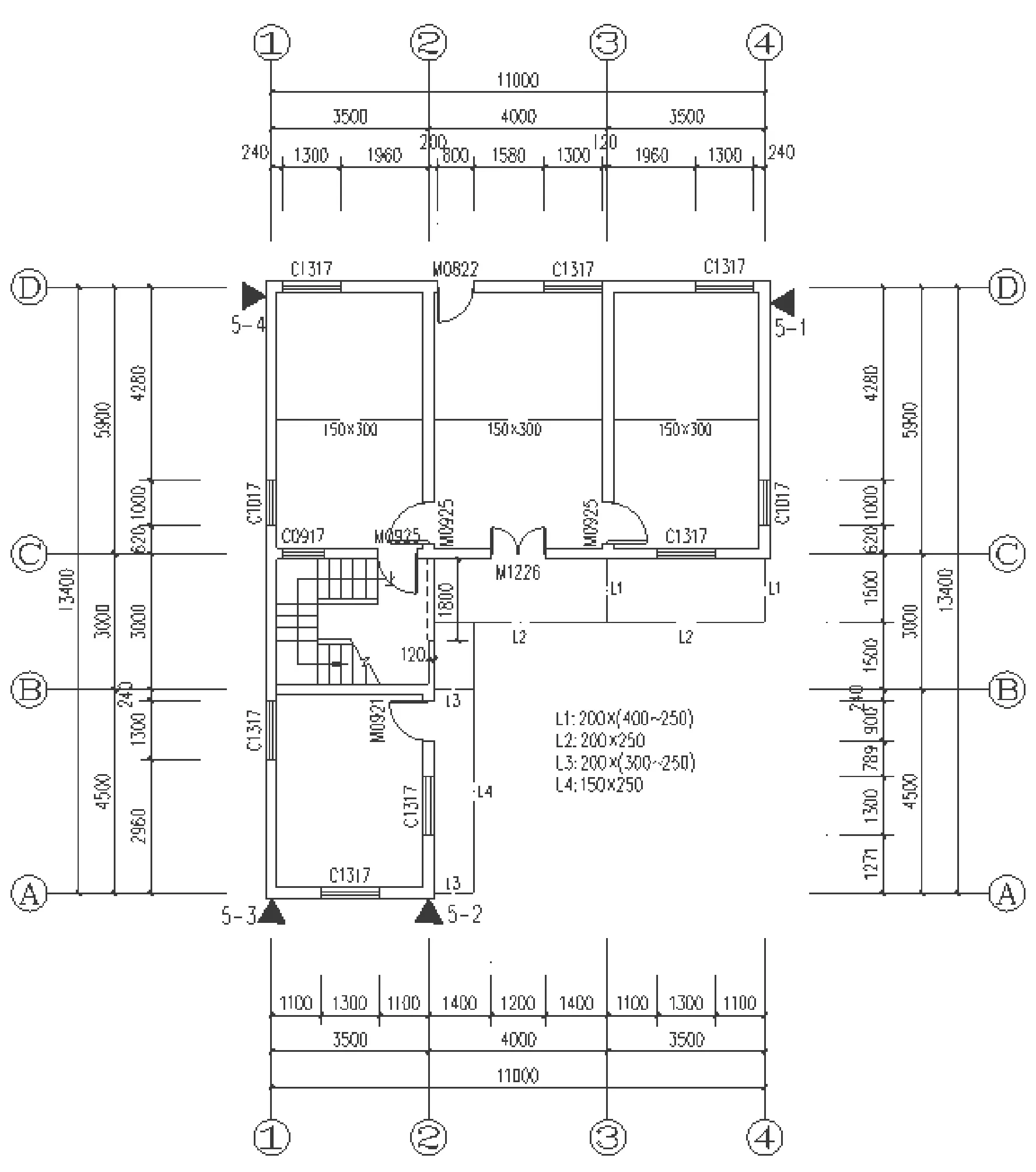
圖10 實例1：一層建筑平面圖

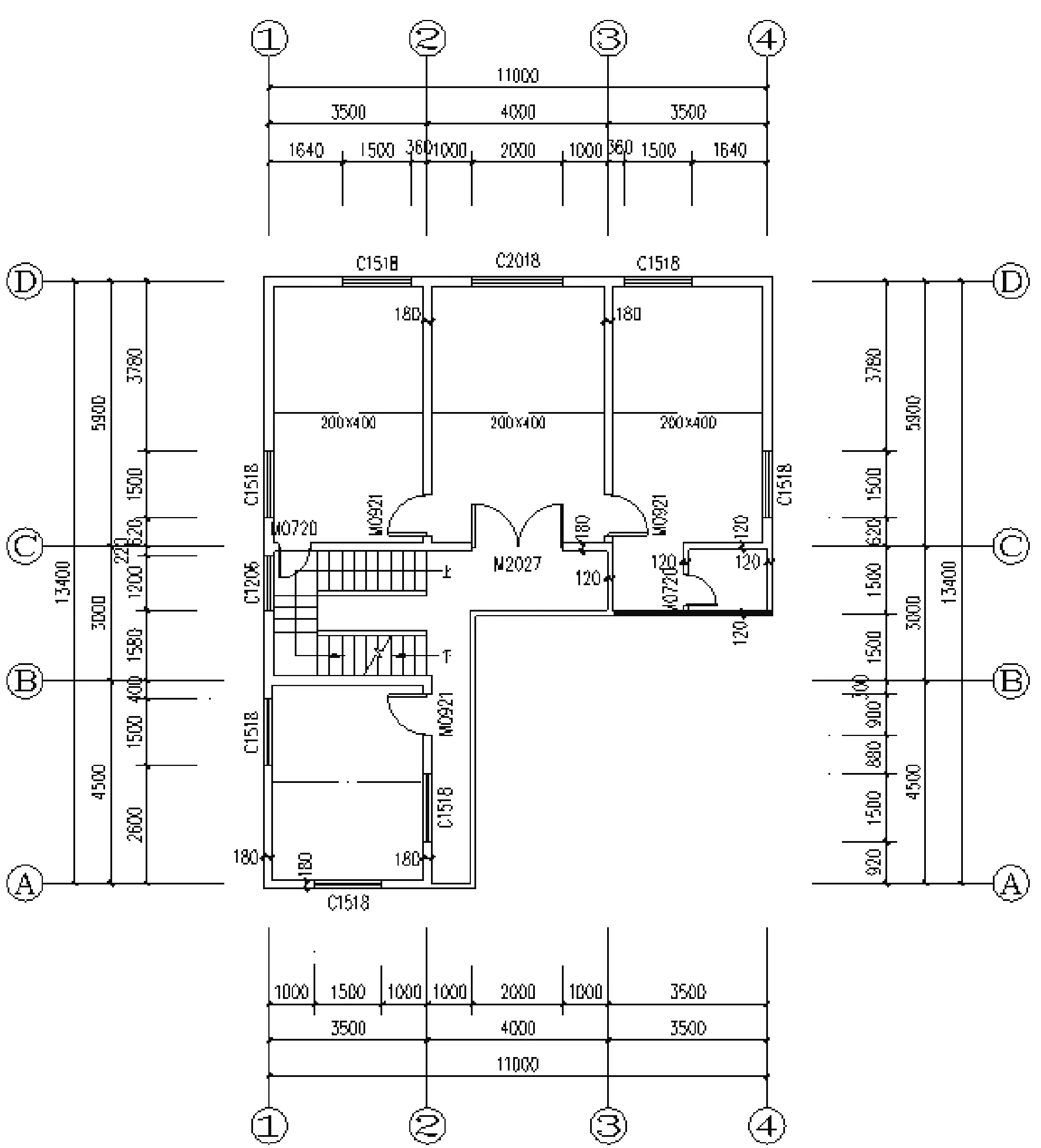
圖11 實例1：二層建筑平面圖

實例2：莆田市涵江區白塘鎮鎮前村孝戶175號房屋，該工程于1987年建造，設計使用年限為50年；未設防，設計地震分組為第三組；其他：采用現澆混凝土樓、屋面板，主要承重墻體為240 mm厚及180 mm厚實心磚墻。房屋四角及縱橫墻交接處均設有混凝土構造柱，樓、屋面板均設置圈梁。經過現場測試，砌筑砂漿為M1。其一、二層建筑平面圖如圖12～圖13所示。

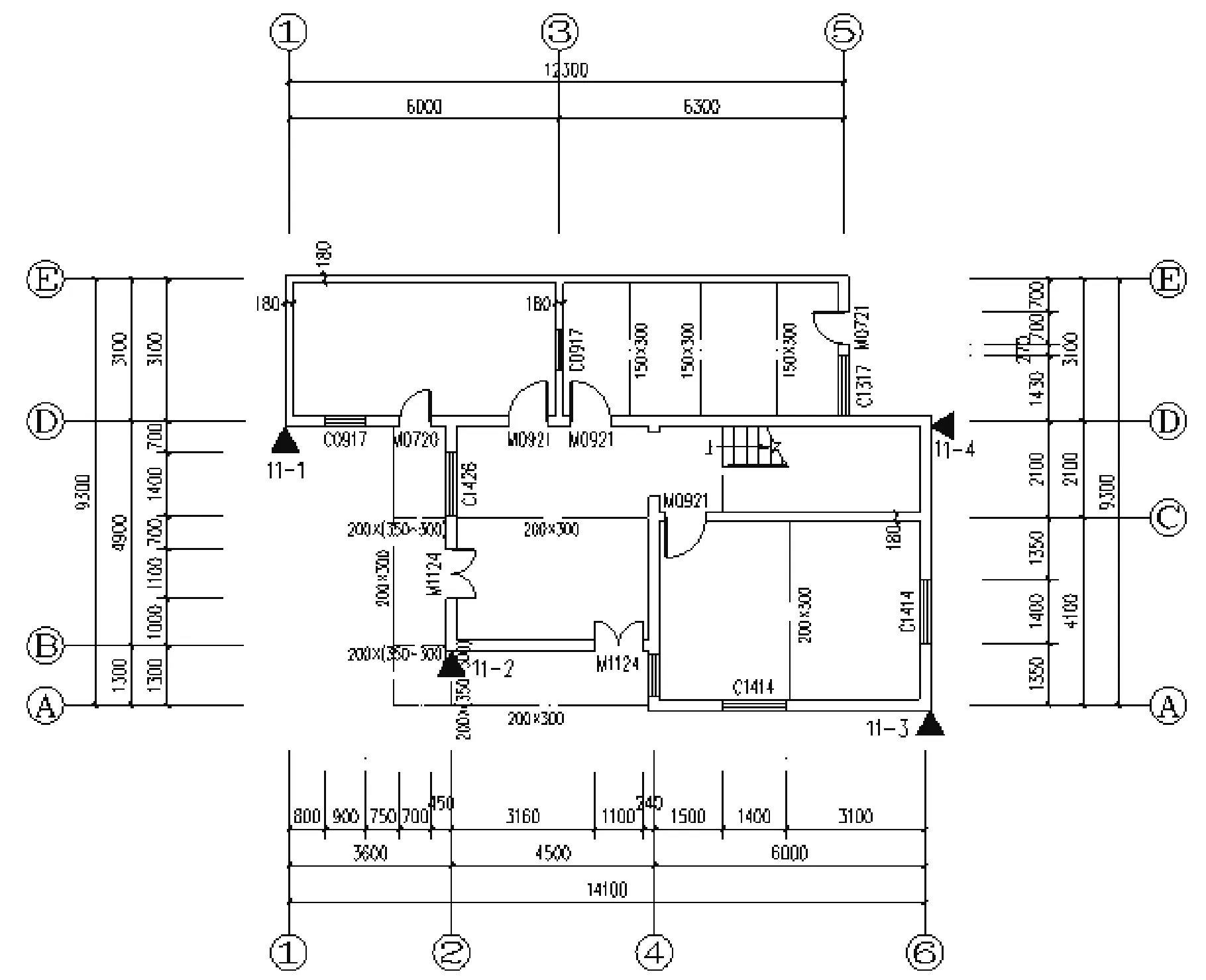
圖12 實例2：一層建筑平面圖

圖13 實例2：二層建筑平面圖

實例3：莆田市荔城區北高鎮汀江村后程口418民房，該工程于1982年建造，設計使用年限為50年；未設防，設計地震分組為第三組；其它：屋面板為鋼筋混凝土現澆板，墻體由240 mm厚磚墻承重。房屋四角及一些縱橫墻交接處均設置混凝土構造柱，屋面板設置圈梁。經過現場測試，砌筑砂漿為M1。其建筑平面圖如圖14所示。

圖14 實例3：建筑平面圖

將3個不同的實際工程分別按前述4種預測方法進行震害預測，預測結果見表11～表13。從表中可以看出：

(1)3個工程的預測結果均表明，改進前的簡化方法震害預測結果偏輕；改進后的簡化方法預測結果與PKPM法和超越強度倍率法的預測結果基本一致；

(2)8度地震作用時，工程實例2采用改進后的簡化方法比PKPM建模分析方法的預測結果高了一個級別。因此，改進的簡化方法是可行的，并具有略高一點的安全系數。

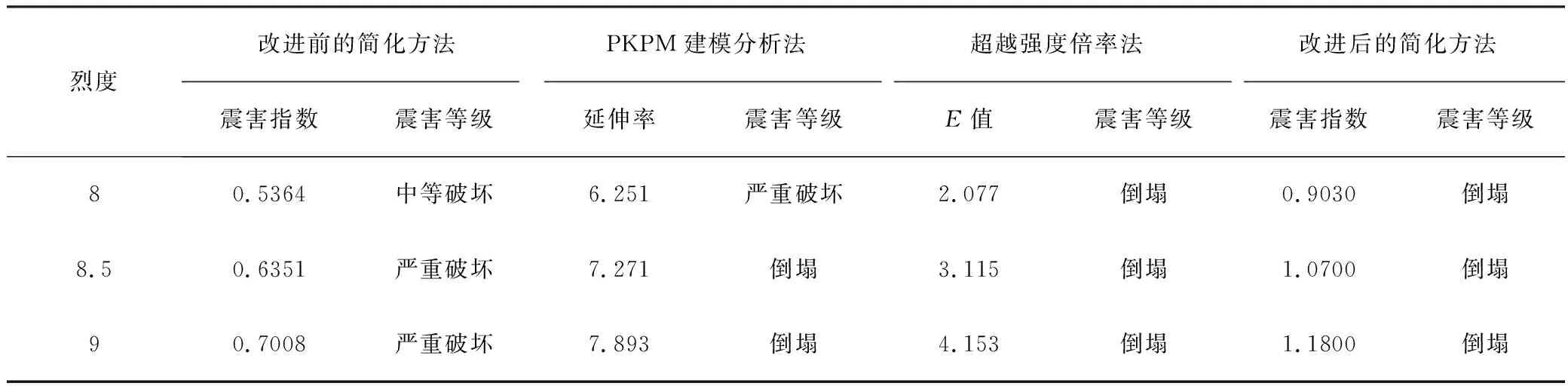
表11 各烈度下結構采用不同單體震害預測方法得到的震害情況的對比(工程實例1)

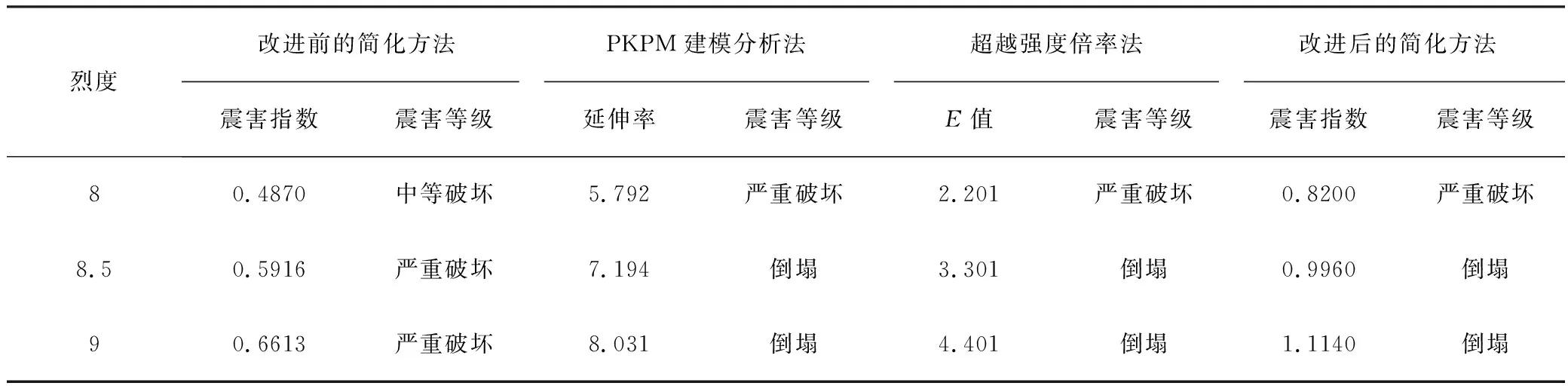
表12 各烈度下結構采用不同單體震害預測方法得到的震害情況的對比(工程實例2)

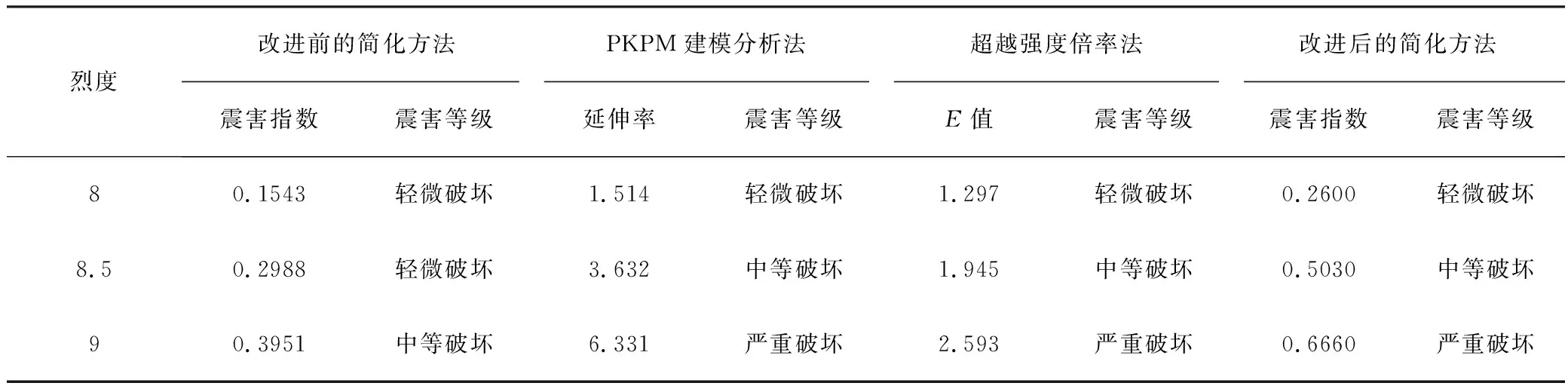
表13 各烈度下結構采用不同單體震害預測方法得到的震害情況的對比(工程實例3)

4 結語

對防災規劃中單體磚混結構的易損性預測簡化方法進行了兩個方面改進。

(1)針對在8度及以上地震作用時結構由原簡化方法預測出來的震害偏輕，對震害指數與抗力的關系式中，8度及以上地震作用所對應的參數進行修正，給出了新的抗力與震害指數的關系式。

(2)考慮到新《抗震規范》相對于舊《抗震規范》不僅理論方面更加趨于成熟，而且其富余度也更高，對延伸率的修正系數中的各項進行修正，包括增加了一項1989版《抗震規范》后的修正系數。

最后，通過三個磚混結構實例，驗證了改進后的簡化方法的可靠性。