簡析平面機構(gòu)自由度的計算方法

金英達 于曉文* 周三合 沈陽工學院機械與運載學院

1 平面機構(gòu)自由度和約束的概念

1.1 平面機構(gòu)的自由度

作平面運動的構(gòu)件相對于定參考系所具有的獨立運動的數(shù)目，稱為構(gòu)件的自由度。因此一個作平面運動的自由構(gòu)件具有三個自由度。

1.2 約束

對非自由體的運動所加的限制稱為約束。

構(gòu)件之間組成運動副后，由于獨立運動受到限制，因而其自由度便隨之減少。每加上一個約束，構(gòu)件便失去一個自由度。平面低副均引入2個約束，平面高副引入1個約束，且自由度減少的數(shù)目等于約束的數(shù)目。

2 平面機構(gòu)自由度的計算公式

設平面機構(gòu)中活動構(gòu)件數(shù)目為 ，形成運動副之前共有3 個自由度。若機構(gòu)中有個低副，則自由度減少個；若機構(gòu)中有 個高副，則自由度減少個。因此，活動構(gòu)件自由度總數(shù)，扣除因形成運動副而減少的自由度，剩下的自由度即為機構(gòu)的自由度，以表示，即

這就是計算平面機構(gòu)自由度的公式。由公式可知，機構(gòu)自由度取決于活動的構(gòu)件數(shù)目以及運動副的性質(zhì)（低副或者高副）和個數(shù)。

3.計算平面機構(gòu)自由度時應注意的幾個問題

3.1 復合鉸鏈：由兩個以上構(gòu)件在同一處構(gòu)成的

重合轉(zhuǎn)動副稱為復合鉸鏈。由 個構(gòu)件匯聚而成的

圖1所示壓力機構(gòu)的自由度計算為：

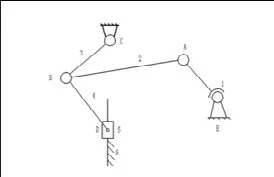
圖1 壓力機構(gòu)運動簡圖

3.2 局部自由度：機構(gòu)中與輸出構(gòu)件運動無關(guān)的自由度，稱為局部自由度。

如圖2所示平面滾子傳動件盤形凸輪機構(gòu)中，滾子繞其自身軸線的轉(zhuǎn)動為機構(gòu)的局部自由度，在計算機構(gòu)的自由度時，應預先將轉(zhuǎn)動副除去不計，或設想將滾子與從動件固聯(lián)在一起作為一個構(gòu)件來考慮。

則圖2 凸輪機構(gòu)運動簡圖

3.3 虛約束：這種重復對構(gòu)件運動形成限制作用的約束或不起獨立限制作用的約束稱為虛約束。在計算機構(gòu)自由度時，應從機構(gòu)的約束數(shù)中減去虛約束數(shù)。

如圖3所示的凸輪-連桿組合機構(gòu)中，在B處

滾子與凸輪機構(gòu)成高副，滾子引入一局部自由度，應除去；在F和F`兩處，豎桿與機架組成導路平行的移動副，引入一虛約束，應除去。

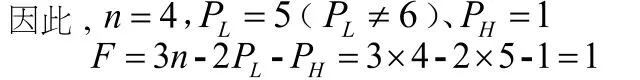
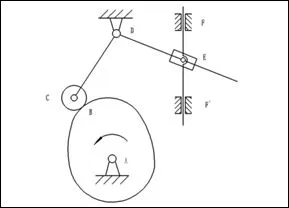
則圖3 凸 輪-連桿機構(gòu)運動簡圖

應當注意，虛約束對機構(gòu)的幾何條件要求較高，因此對機構(gòu)的加工和裝配提出了較高的要求，從機構(gòu)的運動觀點來看是多余的，但能增加機構(gòu)的剛性，改善其受力狀況，因而被廣泛采用。

4 結(jié)論

當機構(gòu)自由度按照上面方法計算完后，即可用此來判斷機構(gòu)的運動是否確定。機構(gòu)的運動是否確定取決于其自由度數(shù)目以及它和原動件數(shù)目之間的關(guān)系。當自由度F＞0時，自由度數(shù)與原動件數(shù)之間的關(guān)系有三種情況：

自由度數(shù)＞原動件數(shù)時，機構(gòu)的運動不能確定；

自由度數(shù)＜原動件數(shù)時，機構(gòu)將在薄弱環(huán)節(jié)被破壞；

自由度數(shù)=原動件數(shù)時，機構(gòu)的運動完全確定。

綜上所述，通過一個原動件輸入一個運動規(guī)律，必然限制機構(gòu)的一個運動自由度。因此，只有當F＞0，且原動件數(shù)目等于自由度時，機構(gòu)才能具有確定的相對運動。