納皮爾的對數模型

王斌儒 甘肅有色冶金職業技術學院 劉延卿 內蒙古通遼市第一中學

16世紀的歐洲大陸，資本主義蓬勃發展，在中世紀萬馬齊喑的科學技術也煥然一新。遠洋航行、天文觀測、船舶制造、軍事創新的要求，源源不斷地為數學的發展提供了不竭的動力，各種新思想新方法層出不窮，其中許多方法旨在簡化計算。

一種辦法是使用三角恒等式：

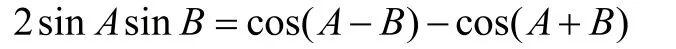
另一種辦法是使用由完全平方公式得到的恒等式：

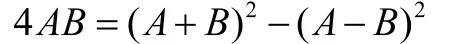
上述方法在實際應用中是不夠的，局限性很強。事實上，我們需要從乘法群到加法群的一個同構映射將乘法運算轉化成加法運算，而這正是納皮爾對數簡化計算的本質。

1 納皮爾對數的起源

納皮爾最初的動機是簡化三角學的計算，特別是在天文學中極為重要的球面三角問題。在納皮爾的時代，一個角的正弦并不是現在熟知的比值，也不是一個確定的數，而是角所對弦長的一半。

我們假設現在給定一個圓和圓心角，AB是圓內任意一條弦，并且C為AB的中點，如圖 1所示：

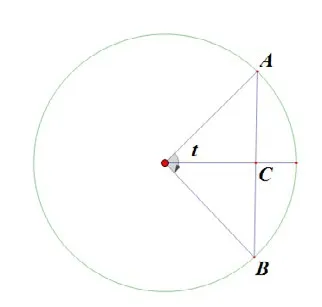
圖 1

此時 在數值上就等于｜ ｜。我們容易發現納皮爾時代正弦值是隨著半徑變化的，半徑越大，正弦值也就越大。

納皮爾由此出發著手建立正弦的對數表。納皮爾選擇半徑為107的圓，他的對數表由間隔一分的107的對數值組成。

2 等比數列與等差數列的對應

表 1

容易看出等比數列中任意兩項的乘積對應等差數列中兩項的和。如果等比數列足夠稠密，理論上可以用上表來計算任意兩個數的乘積（當時主要是三角函數值的乘積）。

基于這個樸素的想法，納皮爾對數橫空出世了。

最終納皮爾選擇了 =1-10-7，這樣等比數列中的各項就緊緊挨在一起了。事實上，這樣導致項的間距過小，為了避免出現小數，加之當時最精確的正弦表是7位有效數字，納皮爾將每一項都乘以107，就是說規定：

表 2

如果用 表示納皮爾的對數，就有

如果將表 2中的數都除以107，就得到表 3。

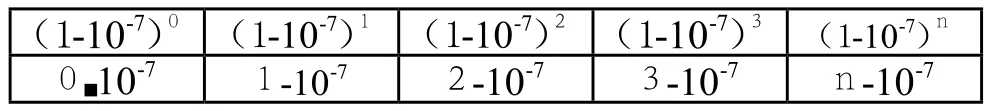
表 3

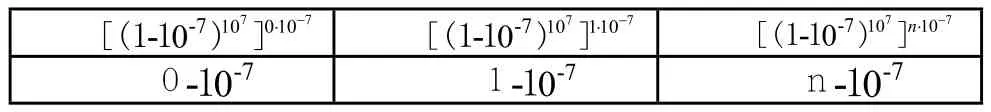
表 4

如果不計比例系數107，可以發現LN(ab)=LN(a)+LN(B)，也就是說納皮爾對數是從到的一個同構映射，把乘法運算轉化成了加法運算。

3 運動學模型

為了計算任意一個數的對數，需要對數函數的連續定義，而不是來自數列的離散定義，我們更加關心的是納皮爾連續的對數定義。

從等比數列到等差數列的對應關系是定義對數函數的關鍵。納皮爾從運動學出發建立了模型。模型源自一個樸素的想法：用一個勻速運動的點代替等差數列，用一個速度成比例的點代替等比數列。納皮爾對數的定義，實際上是通過考慮兩個點沿著兩條直線的運動而給出的，因為納皮爾時代只有物理運動的直觀概念才能為連續變量的定量研究提供理論根據。直線上的動點直觀上被看作是連續的，納皮爾把對數和動點對應起來，直觀上保證了對數的連續性。嚴格地講，動點的速度是連續變化的，納皮爾時代沒有處理連續函數的數學工具，納皮爾模型的嚴格表述需要使用微積分。

下面給出納皮爾的運動學模型，見圖 2。假定線段AB的長度是定值 107。

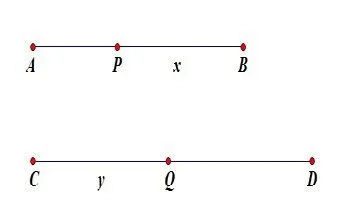
圖 2

CD是一條無限延伸的直線。當t=0時，令P、Q兩點分別從A、C出發。Q在CD上以速度107勻速運動。P在AB上的速度與PB的長度成正比，P的初速度也是107，容易知道P由A到B的速度從107減到 0。

假設t時刻，P到B的距離PB=X，Q到C的距離CQ=y。

納皮爾規定：y是x的對數。我們記作y=LN(x)

我們接下來建立起它和通常意義下對數的聯系。

P在A點時，我們有PB=107同時CQ=0，所以LN(107)=0。

我們通過解一階線性微分方程來看看納皮爾的函數y=LN(x)究竟是什么。

根據納皮爾的運動學模型，我們有

積分得y=-107lnx+c

根據初值條件t=0時，x=107，y=0，因此得 c=107ln107。

做一個簡單的變換，可以有我們更熟悉的形式。如果令

所以如果忽略因子107，我們可以再次得出本質上納皮爾的對數是以 為底的。

我們只要對納皮爾的模型稍稍加以修正就很容易地導出自然對數。我們假定P的速度與AP的長度成正比，Q的速度仍為常數。同時規定t=0時，AP=1，CQ=0。可以得到和上面類似的一個一階線性微分方程，并且以自然對數y=lnx為解。

納皮爾從1594年萌生對數的初步想法，經過20年的深入思考和精密計算，到1614年出版了《奇妙的對數定律說明書》（Mirifici logarithmorum canonis descriptio），正式宣告了對數的發明。200年后，法國數學家拉普拉斯毫不吝嗇地盛贊對數：通過減少體力勞動，使天文學家的生命倍增。