關于多元函數條件極值充分性條件的探討
2018-08-11 03:34:20歐陽夢倩衡陽師范學院
數碼世界 2018年7期
歐陽夢倩 衡陽師范學院
1 引言
在某些實際問題中,考察目標函數:
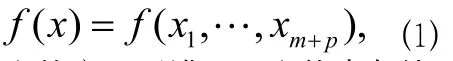
它的變元需滿足一定約束條件:

我們需要尋找目標函數(1)在約束條件(2)下的極值,這樣的問題稱為條件極值。處理條件極值的基本方法為拉格朗日乘數法:首先,構造一個含p個待定乘數的輔助函數
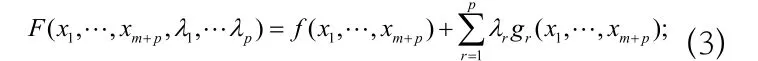
2 極值的充分條件
2.1 約束條件可化為顯式方程
假設(1)和(2)中的函數都連續可微,并滿足正則條件:

可以從(2)中解出
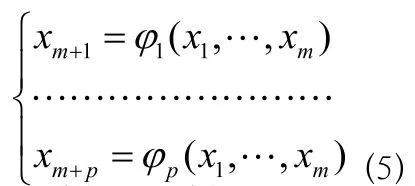
將(5)代入(1)得:

于是,所討論得條件極值問題就化成了求目標函數(6)的無條件極值問題。
例1:在已知周長為2p的一切三角形中,求出面積最大的三角形。
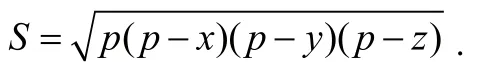
考察目標函數

和約束條件
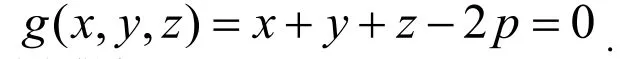
容易得出
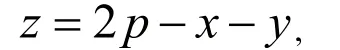
則問題轉化成無條件極值:

由

2.2 將約束條件看作隱函數
2.3 利用海塞(Hasse)矩陣判別
解:設拉格朗日函數為:


所求穩定點為極小值點,且為最小值點。
判別方法二:由海塞矩陣:

為正定矩陣知穩定點即為極小值點,且為最小值點。
3 總結
拉格朗日乘數法是求多元函數條件極值一種常用的方法,利用其求出穩定點后,如何確定穩定點為極值點,應視具體問題而定。

