k次Herschel—師連通圈網(wǎng)絡(luò)

師海忠，陳璐璐

?

k次Herschel—師連通圈網(wǎng)絡(luò)

師海忠，陳璐璐

（西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，甘肅 蘭州 730070）

互連網(wǎng)絡(luò)是超級(jí)計(jì)算機(jī)的重要組成部分，片上互連網(wǎng)絡(luò)是當(dāng)前研究的熱點(diǎn)課題之一。2010年師海忠提出互連網(wǎng)絡(luò)的正則圖連通圈網(wǎng)絡(luò)模型。在這篇文章中利用此模型設(shè)計(jì)出了k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k),證明了HSCC(1,0)是3正則3連通平面Hamiton圖，且HSCC(1,k)是3正則3連通平面Hamiton圖。利用笛卡爾乘積設(shè)計(jì)出了互連網(wǎng)絡(luò)HSCC(1,k)×K2和HSCC(1,k)′Cm，進(jìn)一步研究了HSCC(1,k)′K2和HSCC(1,k)′Cm的一些性質(zhì)。

HSCC(1,k)；Hamilton圖；笛卡爾積；完美對(duì)集

0 引言

互連網(wǎng)絡(luò)是超級(jí)計(jì)算機(jī)的重要組成部分，片上互連網(wǎng)絡(luò)是當(dāng)前研究的熱點(diǎn)課題之一，它的性能在某種程度上決定著超級(jí)計(jì)算機(jī)的性能。互連網(wǎng)絡(luò)通常被模型化為一個(gè)圖，圖的結(jié)點(diǎn)對(duì)應(yīng)處理機(jī)，圖的邊對(duì)應(yīng)通信全過(guò)程。各種已有互連網(wǎng)絡(luò)參見(jiàn)[1,2,4-12]。根據(jù)師海忠在中國(guó)運(yùn)籌會(huì)第十屆學(xué)術(shù)交流會(huì)上提出的超級(jí)計(jì)算機(jī)多種互連網(wǎng)絡(luò)統(tǒng)一體——正則連通圈網(wǎng)絡(luò)，且它的度為3。在這篇文章中，師海忠設(shè)計(jì)出了互連網(wǎng)絡(luò)HSCC(1,0)：將Herschel圖經(jīng)過(guò)4度頂點(diǎn)用4圈代替、3度頂點(diǎn)用3圈代替原來(lái)頂點(diǎn)構(gòu)造了新的網(wǎng)絡(luò)HSCC(1,0)，陳璐璐證明了HSCC(1,0)是3正則3連通平面Hamilton圖，師海忠進(jìn)一步提出了k次Herschel—師連通圈網(wǎng)絡(luò)HSCC(1,k)：用3長(zhǎng)的圈代替HSCC(1,0)中的每個(gè)頂點(diǎn)構(gòu)造了新的網(wǎng)

絡(luò)HSCC(1,1)，重復(fù)k次，我們得到的新的網(wǎng)絡(luò)HSCC(1,k)，陳璐璐證明了k次Herschel—師連通圈網(wǎng)絡(luò)為3正則3連通平面Hamilton圖。師海忠還設(shè)計(jì)出了HSCC(1,k)′K2和HSCC(1,k)′Cm，并提出了如下猜想：

猜想1：HSCC(1,k)′k2是邊不交的兩個(gè)Hamilton的并；

猜想2：HSCC(1,k)′Cm（k=0, m≥3）是邊不交的兩個(gè)Hamilton圈和一個(gè)完美對(duì)集的并。

陳璐璐證明了HSCC(1,0)′k2是一個(gè)邊不交的Hamilton圈和兩個(gè)完美對(duì)集的并，還給出了HSCC (1,k)′K2和HSCC(1,k)′Cm的一些性質(zhì)。

1 基本概念

定義1[1]G的Hamilton圈是指包含G的每個(gè)頂點(diǎn)的圈。

定義2[1]一個(gè)圖若包含Hamilton圈，則稱(chēng)這個(gè)圖是Hamilton圖。

定義3[1]若G至少有一對(duì)相異的不相鄰頂點(diǎn)，則G所具有的k頂點(diǎn)割中最小的k，稱(chēng)為G的連通度，記為k(G);否則定義k(G)為v－1。于是，當(dāng)G是平凡的或不連通時(shí)，k(G)=0。若k(G)≥k，則稱(chēng)G為k連通的。

定義4[1]稱(chēng)圖G是k正則的，如果對(duì)所有的v∈V,有d(v)=k。

定義5 用4長(zhǎng)的圈代替Herschel圖中的4度頂點(diǎn)、3長(zhǎng)的圈代替Herschel圖中的3度頂點(diǎn)，我們得到新的網(wǎng)絡(luò)HSCC(1,0)；再用3長(zhǎng)的圈代替HSCC(1,0)中的每個(gè)頂點(diǎn)，我們得到新的網(wǎng)絡(luò)HSCC (1,1)；重復(fù)k次，我們得到新的網(wǎng)絡(luò)HSCC(1,k)。

定義6[1]若一個(gè)圖具有這樣的一個(gè)圖形，它的邊僅在端點(diǎn)處相交，則該圖稱(chēng)為平面圖。

定義7[1]設(shè)M是E的一個(gè)子集，它的元素是G中的連桿，并且這些連桿中的任意兩個(gè)在G中均不相鄰，則稱(chēng)M為G的對(duì)集（或匹配）；M中一條邊的兩個(gè)端點(diǎn)稱(chēng)為在M下是匹配的。若對(duì)集M的某條邊與頂點(diǎn)v關(guān)聯(lián)，則稱(chēng)M飽和頂點(diǎn)v，并且稱(chēng)v是M飽和的，否則稱(chēng)v是M非飽和的。若G的每個(gè)頂點(diǎn)均為M飽和的，則稱(chēng)M為G的完美對(duì)集。

定義8[2]設(shè)G1=(V1,E1)和G2=(V2,E2)是兩個(gè)無(wú)向圖。G1和G2的笛卡爾乘積是無(wú)向圖，記為G1′G2,其中V（G1′G2）=V1′V2,兩個(gè)不同的頂點(diǎn)x1x2和y1y2(其中x1,y1∈V（G1），x2,y2∈V（G2）)相鄰當(dāng)且僅當(dāng)或者x1=y1，且x2y2∈E（G2），或者x2=y2，且x1y1∈E（G1）。G1和G2稱(chēng)為G1′G2的因子。

定義9 將k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)與K2作笛卡爾乘積生成的網(wǎng)絡(luò)為HSCC (1,k)′K2；k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)與m長(zhǎng)的圈Cm作笛卡爾乘積生成的網(wǎng)絡(luò)為HSCC (1,k)′Cm。

2 主要結(jié)果

2.1 Herschel圖及性質(zhì)

引理[1]Herschel圖是非Hamilton圖。

2.2 k次Herschel-師連通圈網(wǎng)絡(luò)

2.2.1 0次Herschel-師連通圈網(wǎng)絡(luò)

構(gòu)造0次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,0)：在H中，4度頂點(diǎn)用4長(zhǎng)的圈代替、3度頂點(diǎn)用3長(zhǎng)的圈代替，我們將得到新的網(wǎng)絡(luò)HSCC(1,0)。

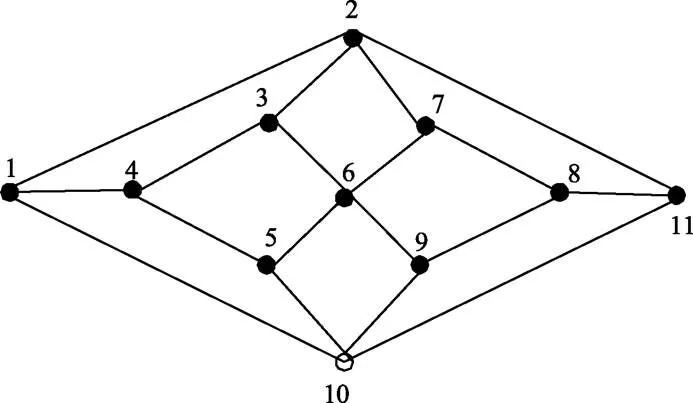
圖1 H

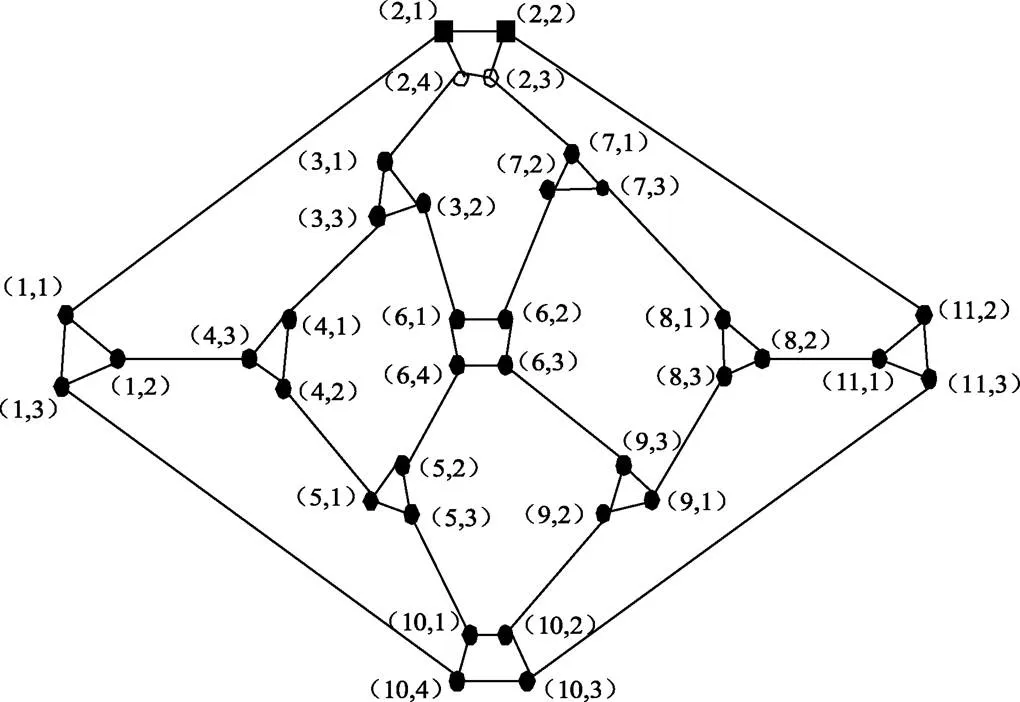
圖2 0次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,0)

由圖2知

定理1 HSCC(1,0)具有如下一些性質(zhì)：

(1)HSCC(1,0)是平面圖；

(2)HSCC(1,0)是3正則的；

(3)HSCC(1,0)是3連通的；

(4)HSCC(1,0)是Hamilton圖。

證明：（1）、（2）顯然

（3）因?yàn)镠SCC(1,0)中每個(gè)頂點(diǎn)的度均為3，則它的最小度d=3。

又由于k≤d（定理[1]），可得，圖HSCC(1,0)的連通度k≤3。

由于圖HSCC(1,0)是非平凡的且是連通的，則k≠0。

若k=1，即HSCC(1,0)所具有的k頂點(diǎn)割中最小的為1，

由圖2知，去掉圖HSCC(1,0)中任何一點(diǎn)后得到的圖仍是連通的，因此k≠1。

若k=2，即HSCC(1,0)所具有的k頂點(diǎn)割中最小的為2，

由圖2知，去掉圖HSCC(1,0)中任何兩點(diǎn)后得到的圖仍是連通的，因此k≠2。

從而k＞2，又由于k≤3，故k=3。即HSCC(1,0)是3連通的。

（4）圖HSCC(1,0)中的Hamilton圈：

（4,1）-（3,3）-（3,2）-（3,1）-（2,4）-（2,1）-（2,2）-（2,3）-（7,1）-（7,2）-（7,3）-（8,1）-（8,3）-（8,2）-（11,1）-（11,2）-（11,3）-（10,3）-（10,2）-（9,2）-（9,1）-（9,3）-（6,3）-（6,2）-（6,1）-（6,4）-（5,2）-（5,1）-（5,3）-（10,1）-（10,4）-（1,3）-（1,1）-（1,2）-（4,3）-（4,2）-（4,1）

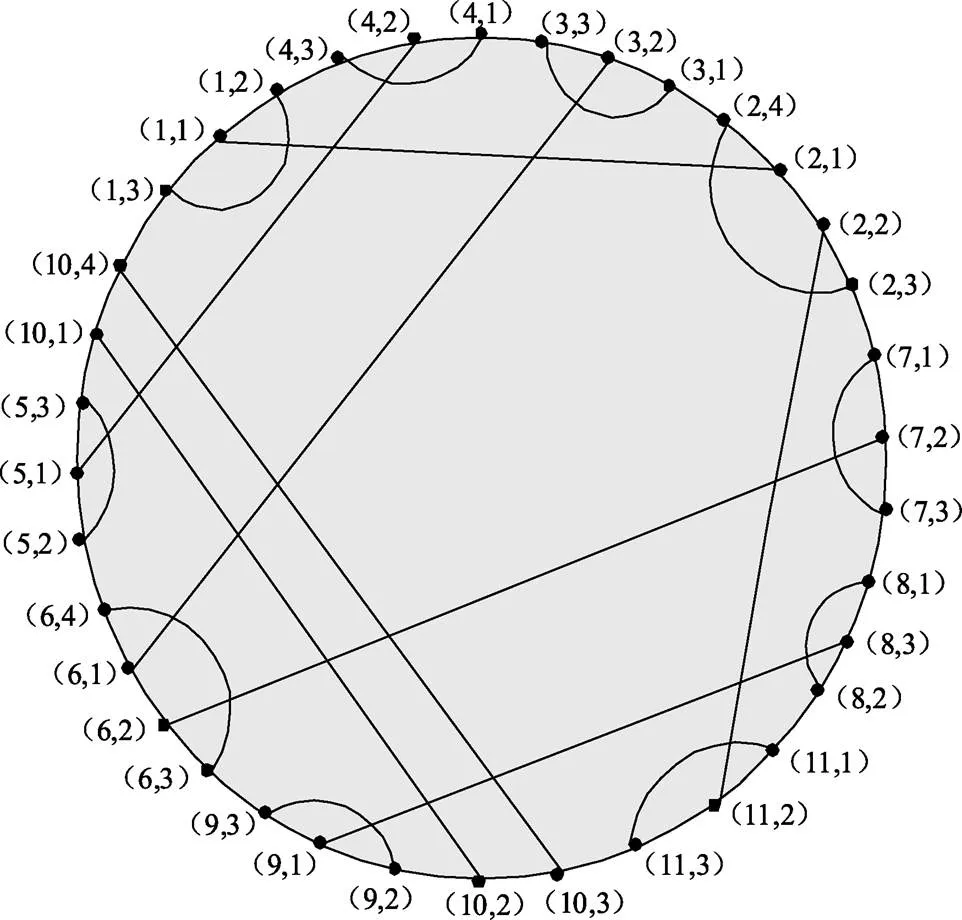
圖3 HSCC(1,0)的圈表示

從而HSCC(1,0)是Hamilton圖。

2.2.2 1次Herschel-師連通圈網(wǎng)絡(luò)

構(gòu)造1次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,1)：用3長(zhǎng)的圈代替HSCC(1,0)中的每個(gè)頂點(diǎn)，我們將得到新的網(wǎng)絡(luò)HSCC(1,1)。

由圖4知

定理2 1次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,1)具有如下一些性質(zhì)：

（1）HSCC(1,1)是平面圖；

（2）HSCC(1,1)是3正則的；

（3）HSCC(1,1)是3連通的；

（4）HSCC(1,1)是Hamilton圖。

證明：（1）、（2）顯然

（3）因?yàn)镠SCC(1,1)中每個(gè)頂點(diǎn)的度均為3，則它的最小度d=3。

從而，圖HSCC(1,1)的連通度k≤3。

由于圖HSCC(1,1)是非平凡的且是連通的，則k≠0。

若k=1，即HSCC(1,1)所具有的k頂點(diǎn)割中最小的為1，

由圖4知，去掉圖HSCC(1,1)中任何一點(diǎn)后得到的圖仍是連通的，

因此k≠1。

若k=2，即HSCC(1,1)所具有的k頂點(diǎn)割中最小的為2，

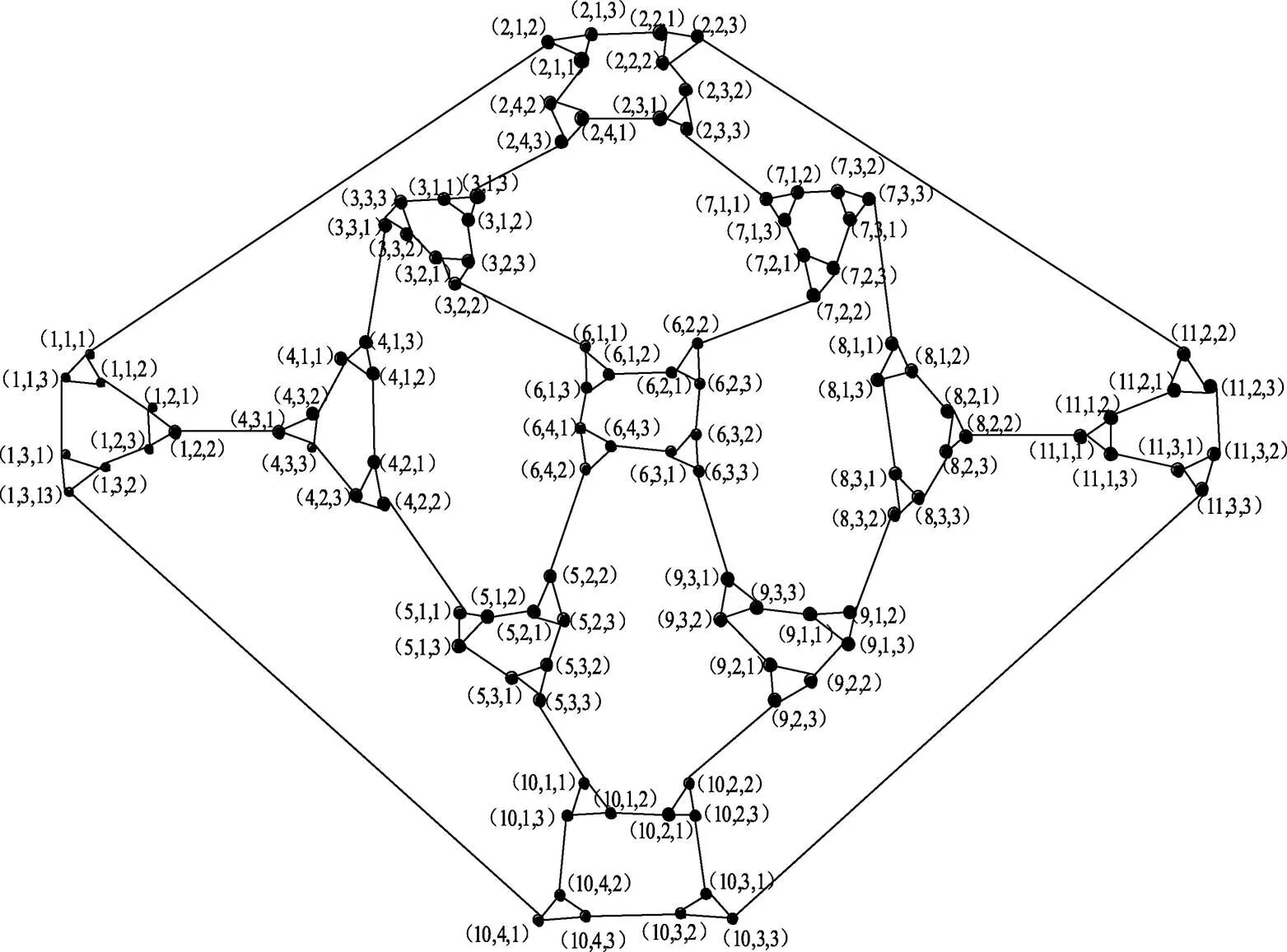
圖4 1次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,1)

由圖4知，去掉圖HSCC(1,1)中任何兩點(diǎn)后得到的圖仍是連通的，

因此k≠2。從而k＞2，又由于k≤3，故k=3。

即HSCC(1,1)是3連通的。

（4）圖HSCC(1,1)中的Hamilton圈：

（4,1,1）-（4,1,3）-（3,3,1）-（3,3,3）-（3,3,2）-（3,2,1）-（3,2,2）-（3,2,3）-（3,1,2）-（3,1,1）-（3,1,3）-（2,4,1）-（2,4,2）-（2,4,3）-（2,1,1）-（2,1,2）-（2,1,3）-（2,2,1）-（2,2,3）-（2,2,2）-（2,3,2）-（2,3,1）-（2,3,3）-（7,1,1）-（7,1,2）-（7,1,3）-（7,2,1）-（7,2,2）-（7,2,3）-（7,3,1）-（7,3,2）-（7,3,3）-（8,1,1）-（8,1,2）-（8,1,3）-（8,3,1）-（8,3,2）-（8,3,3）-（8,2,3）-（8,2,1）-（8,2,2）-（11,1,1）-（11,1,3）-（11,1,2）-（11,2,1）-（11,2,2）-（11,2,3）-（11,3,2）-（11,3,1）-（11,3,3）-（10,3,3）-（10,3,2）-（10,3,1）-（10,2,3）-（10,2,1）-（10,2,2）-（9,2,3）-（9,2,1）-（9,2,2）-（9,1,3）-（9,1,2）-（9,1,1）-（9,3,3）-（9,3,2）-（9,3,1）-（6,3,3）-（6,3,1）-（6,3,2）-（6,2,3）-（6,2,2）-（6,2,1）-（6,1,2）-（6,1,1）-（6,1,3）-（6,4,1）-（6,4,3）-（6,4,2）-（5,2,2）-（5,2,3）-（5,2,1）-（5,1,2）-（5,1,1）-（5,1,3）-（5,3,1）-（5,3,2）-（5,3,3）-（10,1,1）-（10,1,2）-（10,1,3）-（10,4,2）-（10,4,3）-（10,4,1）-（1,3,3）-（1,3,2）-（1,3,1）-（1,1,3）-（1,1,1）-（1,1,2）-（1,2,1）-（1,2,3）-（1,2,2）-（4,3,1）-（4,3,2）-（4,3,3）-（4,2,3）-（4,2,2）-（4,2,1）-（4,1,2）-（4,1,1）

從而圖HSCC(1,1)是Hamilton圖。

表1 圖HSCC(1,1)中Hamilton圈中各頂點(diǎn)與相鄰的點(diǎn)

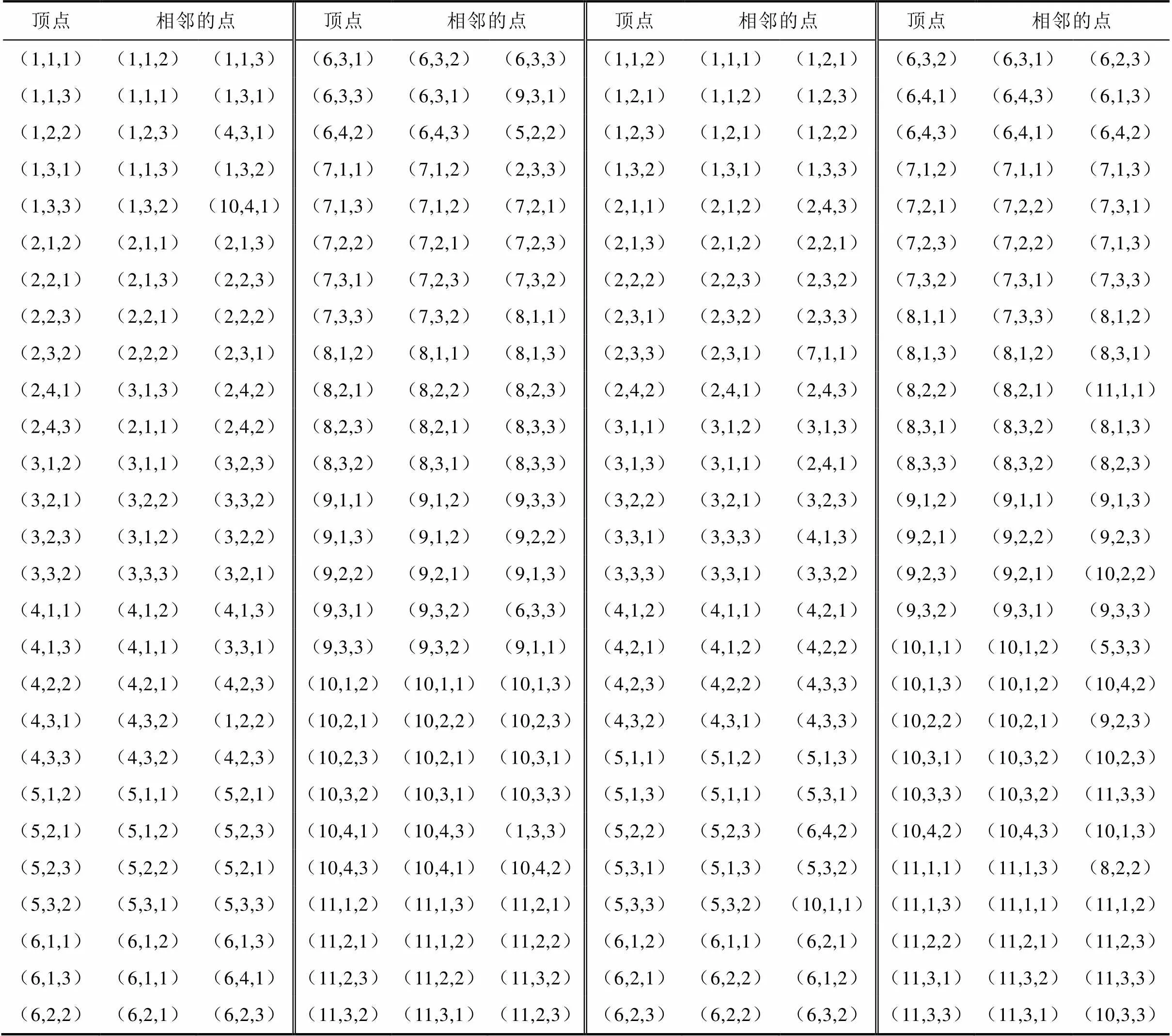
Tab.1 Each vertex and adjacent point in Hamilton circle in HSCC(1,1)

圖5 HSCC(1,1)的圈表示

2.2.3 k次Herschel-師連通圈網(wǎng)絡(luò)

構(gòu)造k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)：用3長(zhǎng)的圈代替HSCC(1,1)中的每個(gè)頂點(diǎn)構(gòu)造了新的網(wǎng)絡(luò)HSCC(1,2)，用3長(zhǎng)的圈代替HSCC(1,2)中的每個(gè)頂點(diǎn)構(gòu)造了新的網(wǎng)絡(luò)HSCC(1,3)，重復(fù)k次，我們得到的新的網(wǎng)絡(luò)HSCC(1,k)。

定理3 k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)具有如下一些性質(zhì)：

（1）HSCC(1,k)是平面圖；

（2）HSCC(1,k)是3正則的；

（3）HSCC(1,k)是3連通的；

（4）HSCC(1,k)是Hamilton圖。

證明：（1）、（2）、（3）顯然

（4）下證HSCC（1,k）是Hamilton圖（數(shù)學(xué)歸納法）。

當(dāng)k=1時(shí)，HSCC(1,k)即為HSCC(1,1)是Hamilton圖，則結(jié)論成立。

假設(shè)當(dāng)k=r-1時(shí)，結(jié)論成立，即HSCC(1,r-1)是Hamilton圖，

也即HSCC(1,r-1）有一個(gè)Hamilton圈記為CHSCC(1,r-1)。取CHSCC(1,r-1)中的任意頂點(diǎn)b、c、d是與a相鄰的三個(gè)頂點(diǎn)，則CHSCC(1,r-1)中必含邊ab、ac、ad中的兩條邊，假設(shè)CHSCC(1,r-1)中含邊ab、ac（見(jiàn)圖6）。

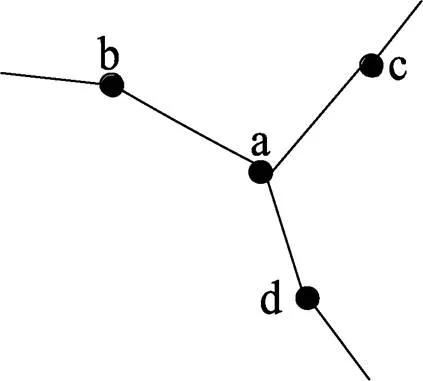
圖6 HSCC(1,r-1)的局部表示

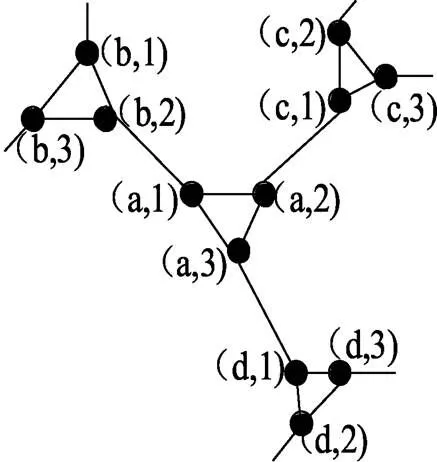
圖7 HSCC(1,r)的局部表示

當(dāng)k=r時(shí)，即當(dāng)用3長(zhǎng)的圈代替CHSCC(1,r-1)中的每一個(gè)頂點(diǎn)時(shí)，假設(shè)用圈（a,1）-（a,2）-（a,3）-（a,1）代替a，用圈（b,1）-（b,2）-（b,3）-（b,1）代替 b, 用圈（c,1）-（c,2）-（c,3）-（c,1）代替c, 用圈（d,1）-（d,2）-（d,3）-（d,1）代替d,則a、b、c、d四點(diǎn)變化后的圖為圖7。用路P=（（b,2），（a,1）, (a,3）, (a,2）, (c,1）)代替路（bac）后，得到的圈仍為Hamilton圈，同理，CHSCC(1,r-1)中的任意點(diǎn)都有如上性質(zhì)。從而CHSCC(1,r-1)中所有點(diǎn)用3長(zhǎng)的圈代替，且用上面方式代替原來(lái)的路，得到的圈CHSCC(1,r)即為HSCC(1,r)的一個(gè)Hamilton圈。

綜上所述，由數(shù)學(xué)歸納法知HSCC(1,k)是Hamilton圖。

2.3 k次Herschel-師連通圈網(wǎng)絡(luò)的3維變體

2.3.1 HSCC（1,k）與K2的笛卡爾積網(wǎng)絡(luò)

根據(jù)文獻(xiàn)[6]的思想設(shè)計(jì)出了新的互連網(wǎng)絡(luò)HSCC(1,k)′K2

定理4 HSCC(1,k)′K2可以分解成一個(gè)邊不交的Hamilton圈和兩個(gè)完美對(duì)集的并。

圖HSCC(1,0)′K2的Hamilton圈：

001-002-004-005-006-007-008-009-010-011-012-013-014-015-016-017-018-019-020-021-022-023-024-025-026-027-028-029-030-031-032-033-034-035-036-003-103-136-135-134-133-132-131-130-129-128-127-126-125-124-123-122-121-120-119-118-117-116-115-114-113-112-111-110-109-108-107-106-105-104-102-101-001

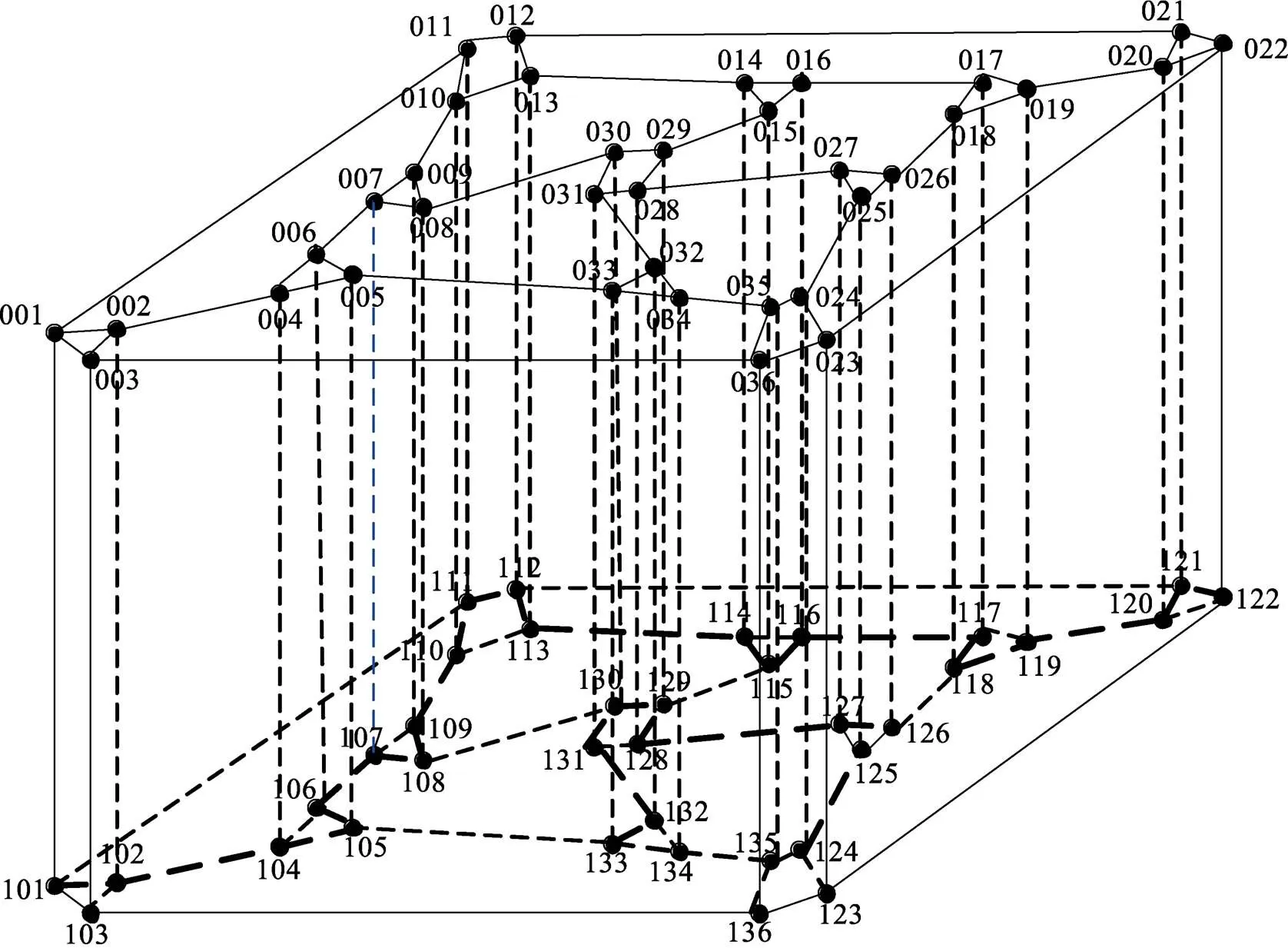
圖8 HSCC(1,0)與K2的笛卡爾積網(wǎng)絡(luò)HSCC(1,0)′K2

圖HSCC(1,0)′K2的兩個(gè)完美對(duì)集：

（1）002-003，001-011，004-006，007-009，005-034，008-030，010-013，012-021，014-016，029-015，031-028, 017-019，020-022，027-025，026-018，024-035，023-036，032-033，102-103，101-111，104-106，107-109，110-113，112-121，105-133，108-130，110-113，114-116，117-119，120-122，118-126，125-127，128-131，132-134，124-135，123-126

（2）001-003，101-103，002-102，004-104，005-105，006-106，007-107，008-108，009-109，010-110，011-111，012-112，013-113，014-114，015-115，016-116，017-117，018-118，019-119，020-120，021-121，022-122，023-123，024-124，025-125，026-126，027-127，028-128，029-129，030-130，031-131，032-132，033-133，034-134，035-135，036-136

定理5 k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)與K2的笛卡爾積網(wǎng)絡(luò)HSCC(1,k)′K2的一些性質(zhì)：

（1）HSCC(1,k)′K2是4正則4連通的；

（2）HSCC(1,0)′K2有72個(gè)頂點(diǎn)，有144條邊；

（3）HSCC(1,k)′K2（k≥1）有72′3k個(gè)頂點(diǎn)，有108＋36′3k+1條邊；

（4）HSCC(1,0)′K2是Hamilton圖。

證明：（1）由定理3知HSCC(1,k)是3正則3連通的，而K2是1正則1連通的，

故HSCC(1,k)′Cm是4正則4連通的。

（2）、（3）顯然

（4）由定理4知HSCC(1,0)′K2是Hamilton圖

猜想1仍是開(kāi)的

2.3.2 HSCC(1,k)與Cm的笛卡爾積網(wǎng)絡(luò)

根據(jù)文獻(xiàn)[6]的思想設(shè)計(jì)出了新的互連網(wǎng)絡(luò)HSCC(1,k)′Cm

定理6 k次Herschel-師連通圈網(wǎng)絡(luò)HSCC(1,k)與Cm的笛卡爾積網(wǎng)絡(luò)HSCC(1,k)′Cm的一些性質(zhì)：

（1）HSCC(1,k)′Cm是5正則5連通的；

（2）HSCC(1,0)′Cm有36 m個(gè)頂點(diǎn)，有108+ 36 m條邊；

（3）HSCC(1,k)×Cm（k≥1）有36 m′3k個(gè)頂點(diǎn)，有108+72 m′3k條邊；

（4）HSCC(1,0)′C3是Hamilton圖。

證明：（1）由定理3知HSCC(1,k)是3正則3連通的，而Cm是2正則2連通的，

故HSCC(1,k)′Cm是5正則5連通的。

（2）、（3）顯然

（4）HSCC(1,0)×C3的Hamilton圈：

001-002-004-005-006-007-008-009-010-011-012-013-014-015-016-017-018-019-020-021-022-023-024-025-026-027-028-029-030-031-032-033-034-035-036-003-103-136-135-134-133-132-131-130-129-128-127-126-125-124-123-122-121-120-119-118-117-116-115-114-113-112-111-110-109-108-107-106-105-104-102-202-204-205-206-207-208-209-210-211-212-213-214-215-216-217-218-219-220-221-222-223-224-225-226-227-228-229-230-231-231-232-233-234-235-236-203-201-101-001

故HSCC(1,0)′C3是Hamilton圖。

猜想2仍是開(kāi)的

4 結(jié)論

本文給出了HSCC(1,k)（k≥0）的定義以及一些性質(zhì)，證明了HSCC(1,k)是Hamilton圖，以及HSCC(1,k)與K2、HSCC(1,k)與Cm的笛卡爾積的一些性質(zhì)。

[1] BONDY J A and MURTY U S R. Graph Theory with Applications[M]. Macmillan Press Ltd, London and Basingstlke, 1976.

[2] 徐俊明. 組合網(wǎng)絡(luò)理論[M]. 北京: 科學(xué)出版社, 2007.

[3] Xu Junming .A First Course in Graph Theory[M]. Science Press, Beijing, 2015.

[4] 師海忠. 正則連通圈: 多種互連網(wǎng)絡(luò)的統(tǒng)一模型[C]. 北京: 中國(guó)運(yùn)籌學(xué)會(huì)第十一屆學(xué)術(shù)交流會(huì)文集, 2010: 202-208.

[5] 師海忠. 幾類(lèi)新的笛卡爾乘積互連網(wǎng)絡(luò)[J]. 計(jì)算機(jī)科學(xué), 2013, 40(6A): 265-270.

[6] Shi, H. and Shi, Y. (2015) A New Model for Interconnection Network:K-Hierarchcal Ring and R-Layer Graph Network. http://vdisk.weibo.com/s/dlizJyferZ-ZI.

[7] Shi, H. and Shi, Y. (2015) A Hierarchcal Ring Group- theoretic Model for Interconnection Networks. http://vdisk. weibo.com/s/dlizJyfeBX-2J.

[8] Shi, H. and Shi, Y. (2015) Cell-Breading Graph Model for Interconnection Networks. http://vdisk.weibo.com/s/dlizJyfesb05y

[9] 張欣, 師海忠. 交叉立方體連通圈網(wǎng)絡(luò)的Hamilton分解[J]. 軟件, 2015, 36(8): 92-98.

[10] 常立婷, 師海忠. 基于超立方體和圈的細(xì)胞分裂生長(zhǎng)網(wǎng)絡(luò)及其性質(zhì)[J]. 軟件. 2017, 38(9): 141-149.

[11] 師海忠, 汪生龍. 關(guān)于煎餅網(wǎng)絡(luò)及層次環(huán)煎餅網(wǎng)絡(luò)的幾個(gè)猜想[J]. 軟件. 2018(01): 94-100.

[12] 胡艷紅, 師海忠. 關(guān)于冒泡排序連通圈網(wǎng)絡(luò)猜想的一個(gè)注記[J]. 軟件. 2016(01): 97-100.

k Herschel – Shi Connected Cycles Networks

SHI Hai-zhong, CHEN Lu-lu

(College of Mathematics and Statistics, Northwest Normal University, Lanzhou Gansu 730070, China)

An Interconnection network is an important part of a supercomputer. On-chip interconnection network is one of the hot topics in the current research.In 2010,Hai-zhong Shi proposed the model of regular graph connected cycles.In this paper, we design the network model of regular graphs of interconnected networks HSCC(1,k) and prove that HSCC(1,0) is a 3-regular 3-connected planar Hamilton graph,and HSCC(1,k) is a 3-regular 3-connected planar Hamilton graph.By using the Cartesian product, the interconnect network HSCC(1,k)×K2and HSCC(1,k)×Cmare designed, and some properties of HSCC(1,k)×K2and HSCC(1,k)×Cmare further studied.

HSCC(1,k); Hamilton graph; Cartesian product; Perfect matching

TN393

A

10.3969/j.issn.1003-6970.2018.07.015

師海忠(1962-)，男，博士，教授，互連網(wǎng)絡(luò)設(shè)計(jì)與分析、有（無(wú)）向圖語(yǔ)言、隨機(jī)圖語(yǔ)言、（V，R）-語(yǔ)言，（V，R）-半群，網(wǎng)絡(luò)科學(xué)與語(yǔ)言等；陳璐璐(1993-)，女，碩士研究生，主要研究方向：網(wǎng)絡(luò)科學(xué)與語(yǔ)言。

本文著錄格式：師海忠，陳璐璐. k 次Herschel— 師連通圈網(wǎng)絡(luò)[J]. 軟件，2018，39（7）：72—78