弧齒線擺線圓柱齒輪副的幾何參數與承載力分析

柏華文，黃文杰，宋愛平，彭云

(揚州大學機械工程學院，江蘇揚州 225127)

0 引言

齒輪傳動是機械傳動效率最高的傳動機構。在以前的研究中，圓柱齒輪的齒廓主要分為3種：漸開線、擺線、圓弧形[1]。圓柱齒輪的齒線主要分為直齒、斜齒、人字齒3種。這些齒輪都已廣泛應用于機械傳動。文中分析的弧齒線擺線圓柱齒輪是一種新型的圓柱齒輪,其主要特點是:齒線是圓弧的一部分[1]；齒廓分為兩部分，分度圓外為一段圓弧，分度圓內為根據嚙合原理所做出的齒峰圓弧的共軛曲線[2],其外形如圖1所示。

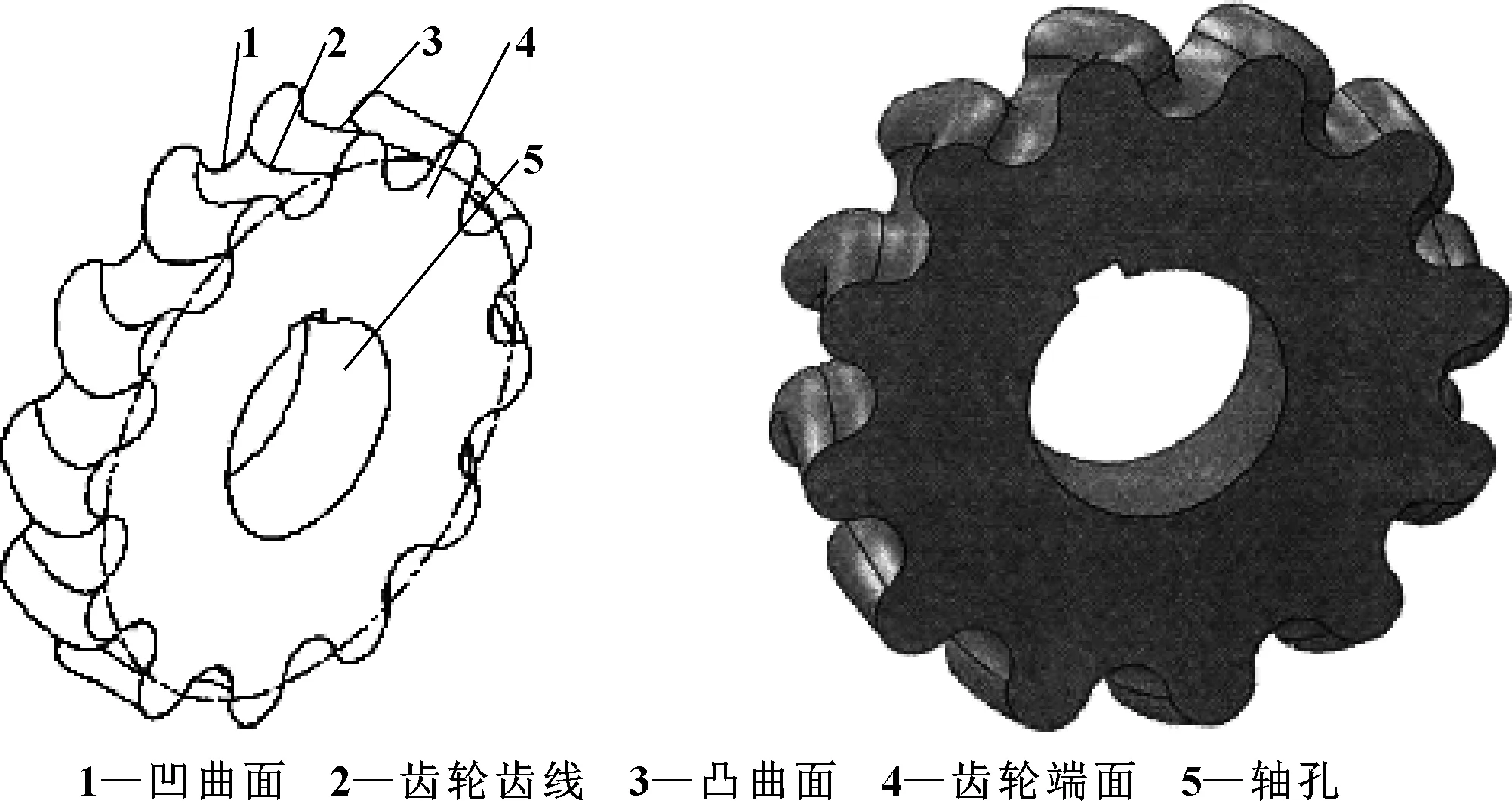
圖1 弧齒線擺線圓柱齒輪

對于弧齒線擺線圓柱齒輪，目前還缺少對其進行受力分析的方法，作者采用有限元分析法對齒面接觸應力和齒根彎曲應力進行分析，探究弧齒線半徑對其傳動強度的影響。

1 弧齒線擺線圓柱齒輪的基本參數

1.1 弧齒線擺線圓柱齒輪的基本參數

1.1.1 分度圓

分度圓是為了便于齒輪設計和制造而選擇的一個尺寸參考。齒輪分度圓具有標準的模數和標準的壓力角，所以取它作為齒輪各部分尺寸的計算基礎。取弧齒線擺線圓柱齒輪的分度圓半徑為a=2l/(1+k),其中l為齒輪副中心距，k為齒輪傳動比。

1.1.2 模數

在弧齒線擺線圓柱齒輪的分度圓截面處各點的周向齒厚相等、周向齒槽相等[3]，即Ts=Tc、Hs=Hc，如圖2所示。這里提出一個新的齒輪參數——周向模數mc,其值為分度圓直徑與齒數之比。

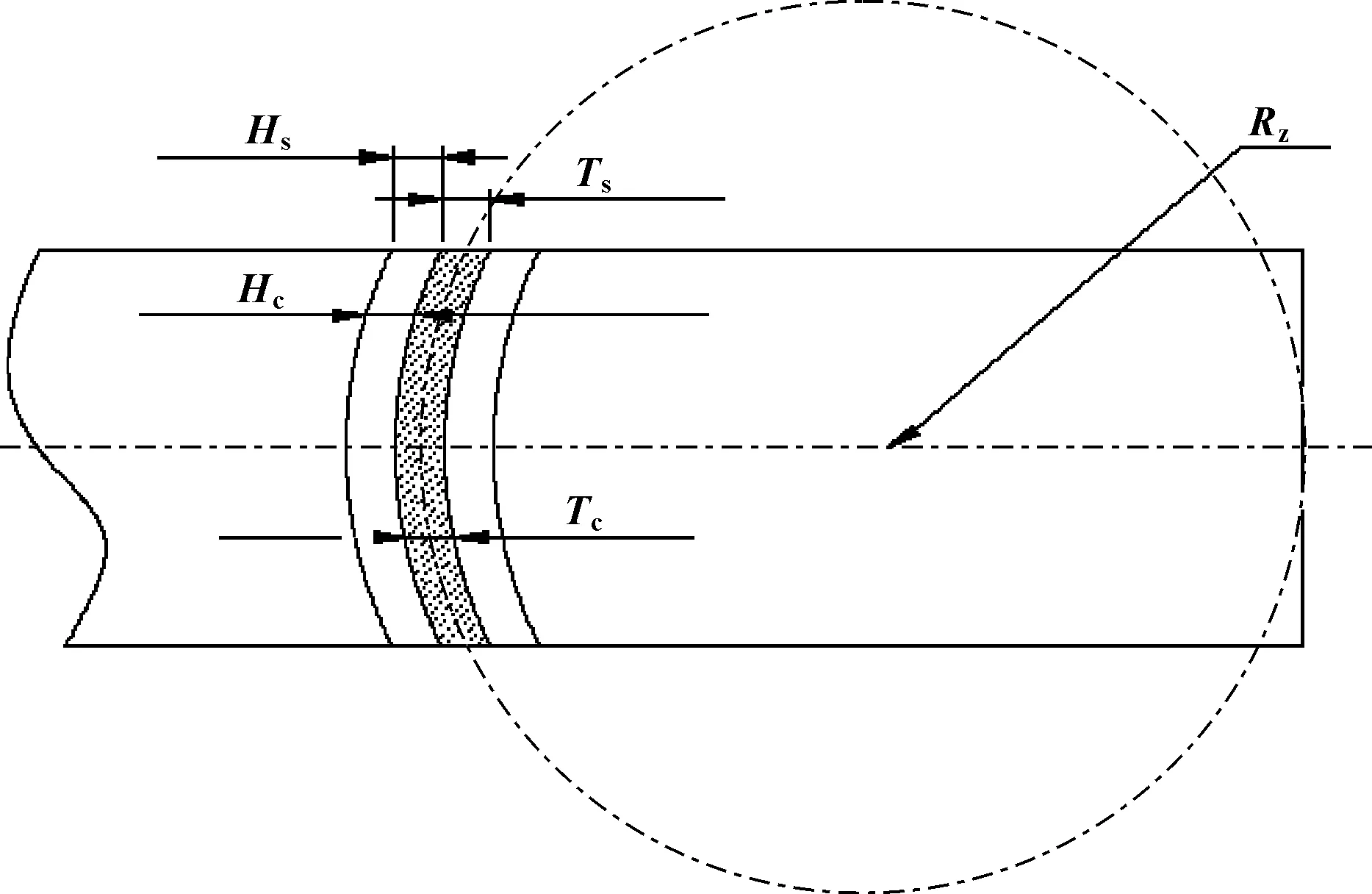
圖2 弧齒線擺線圓柱齒輪幾何參數

1.1.3 齒峰圓弧半徑及壓力角

弧齒線擺線圓柱齒輪的一些基本參數與傳統漸開線齒輪的參數類似，例如，對于傳統的漸開線齒輪，齒廓的不同位置有不同的壓角，弧齒形擺線圓柱齒輪也具有相同的特性。在圖3(a)中，齒峰為一段圓弧，力Fn朝向圓弧中心O3。假設βi是旋轉角，ai是齒峰圓的半徑，而αi是相應的壓力角。

如圖3(a)所示，根據三角形的正弦定理:

(1)

一對嚙合齒輪在分度圓處具有相同的壓力角，k是傳動比。假設齒輪1和齒輪2是一對嚙合齒輪。如圖3(b)所示，r1表示齒輪1齒峰圓的半徑，b1代表從齒輪的中心到齒峰圓弧的中心長度，a1表示齒輪1的分度圓半徑。齒峰圓弧的一半所對應的角度β1=π/2z1，齒谷擺線的一半所對應的角度也是相同的角度β2=π/2z1(其中z1為齒輪1的齒數)。在圖3(b)中，根據方程(1)，可以得到以下方程：

(2)

由圖3(c),同理可得與齒輪1相嚙合的齒輪2的方程:

(3)

其中：α表示齒輪1的節圓壓力角,γ和α是互余的角度。a2=ka1,b2=kb1,β2=π/2z2。

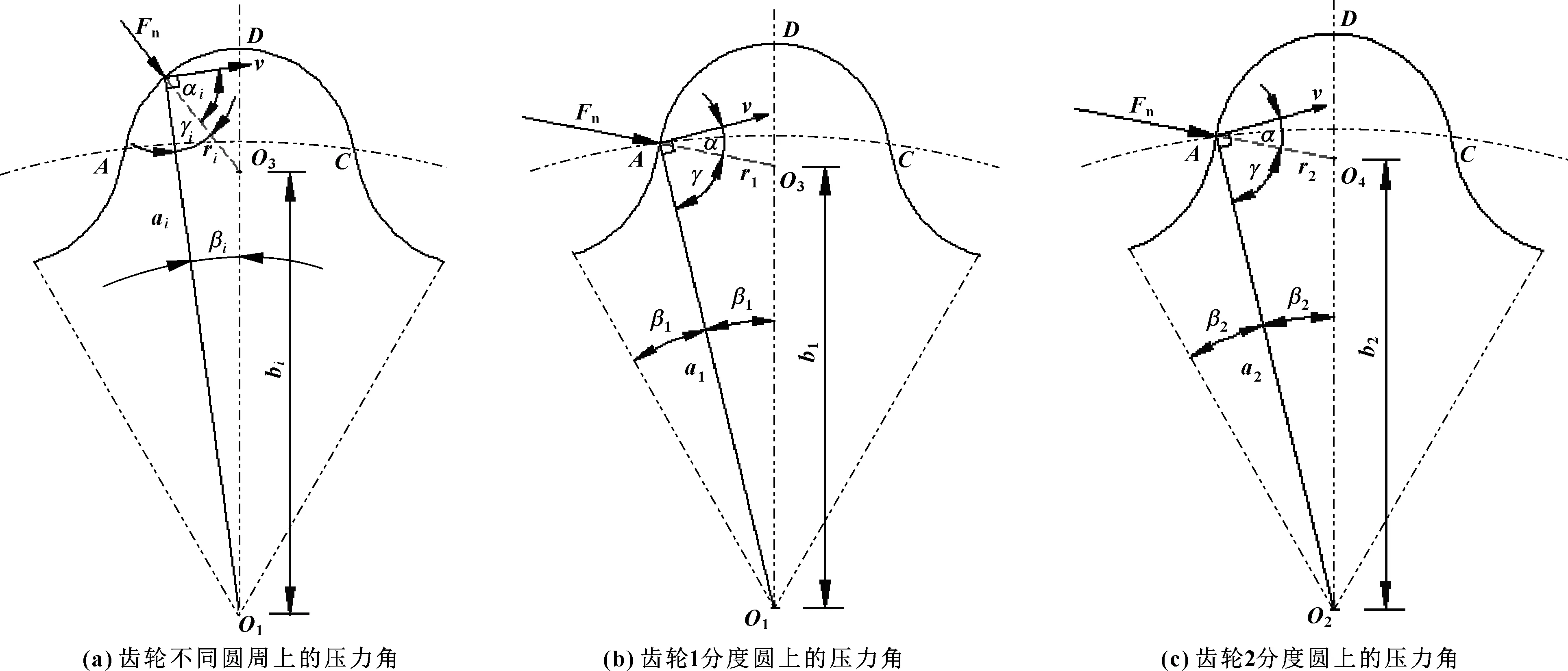
圖3 弧齒線擺線圓柱齒輪壓力角

1.2 齒廓方程

1.2.1 齒峰曲線方程

參照圖4，建立了一種笛卡爾坐標系XO1Y，假設齒數比k=z2/z1，齒輪1作為傳動齒輪。在△O1O3S1中，根據三角形的余弦定理：

(4)

齒輪1的半齒峰圓弧T1S1的參數方程可以表示為：

(5)

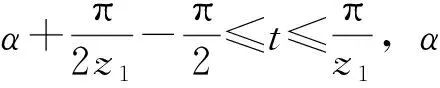
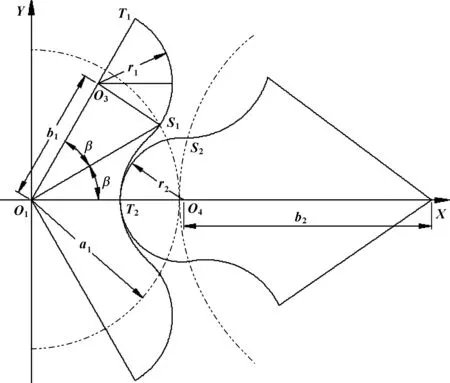
圖4 齒輪副嚙合齒廓

1.2.2 齒谷曲線方程

由圖5可知：當齒輪1沿著中心O1順時針旋轉角度θ,齒輪2將沿著中心O2逆時針旋轉角度θ/k。令齒輪2逆時針旋轉并令齒輪1不動。齒輪2曲線T2S2和齒輪1曲線Q1S1相嚙合,G(x2，y2)是嚙合點，P是兩個齒輪節圓的交點。嚙合點G的法線必然穿過齒輪2的齒峰圓中心點O4以及節點P。因此，點G、P、O4在直線GO4上。讓直線O1F∥O4G,F是直線O1F和直線O2O4的交點,δ是直線O1F和X軸的夾角。讓EF垂直于笛卡爾坐標系的X軸，E為垂足，讓直線O4A平行于X軸，A是交點。讓CG垂直于直線AC,C為垂足。通過幾何關系，可以得到以下關系：△O1FE∽△O4GC, △O2PO4∽△O2O1F, △O2O4A∽△O2FD，可以得出以下結論:

∠GO4C=∠FO1E=δ

(6)

(7)

(8)

(9)

O1F=(O1E2+FE2)1/2=

(10)

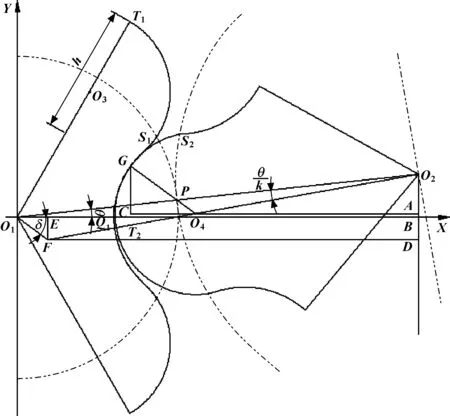
圖5 任意旋轉角度下的齒谷擺線的嚙合

齒輪1的齒谷擺線的1/2可以用笛卡爾坐標系表示為下面的方程：

x2=O1B-O4A-O4C=(k+1)·a1·cosθ-

(11)

y2=O2B-O2A+GC=(k+1)·a1·cosθ-

(12)

其中：

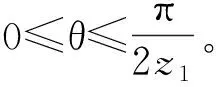
1.2.3 齒線半徑與位置角的關系

如圖6所示，有笛卡爾坐標系(O,X,Y,Z)。XOY平面穿過齒輪中間部分，Z軸與齒輪軸重合。將橫向剖面投影到中間部分，齒輪的中間部分可以被視為齒廓。

假設B是齒輪的齒寬，RZ是圓弧齒的半徑。弧齒線位置角對應弧長的方程為：

(13)

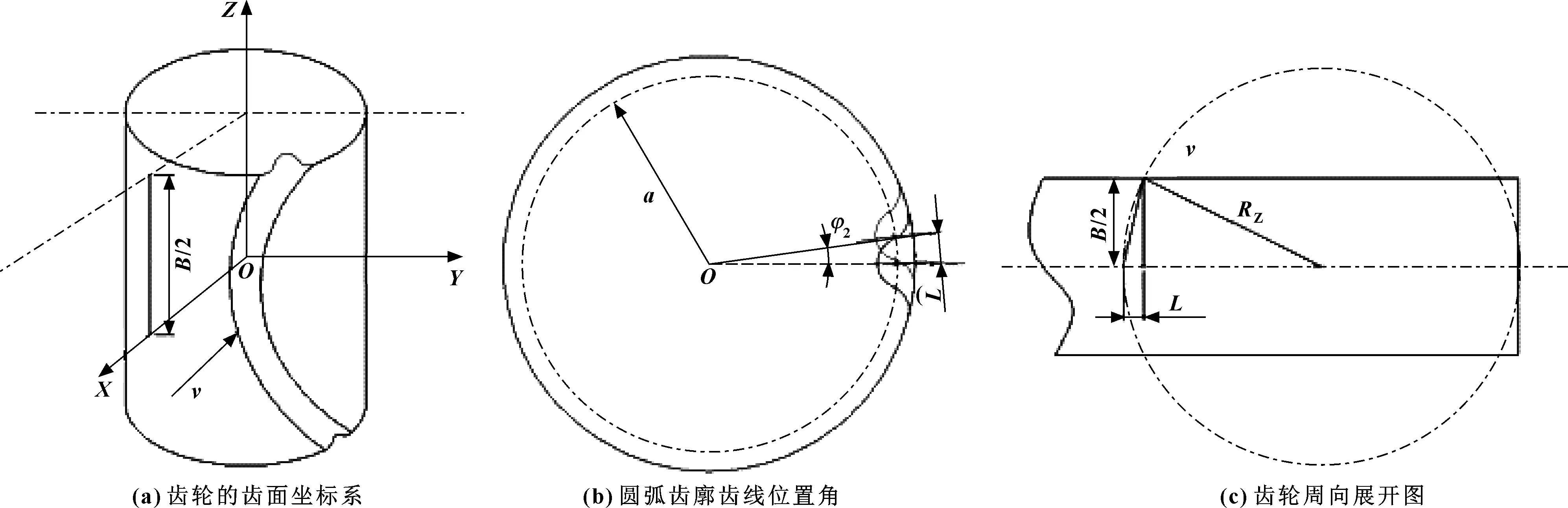
圖6 齒線位置角φ2與齒輪的周向展開

可以算出位置角φ2為：

(14)

其中：a為分度圓半徑。

1.3 重合度

重合度是齒輪傳動的一個很重要的概念,是齒輪傳動的連續性及平穩性評價的重要指標。實際嚙合線的長度與周節的比值稱為重合度。參照人字齒輪副重合度的計算方法，弧齒線擺線圓柱齒輪的重合度ε由端面重合度εα和軸向重合度εβ組成[4]，即

ε=εα+εβ

(15)

由于弧齒線擺線圓柱齒輪的齒廓比較特殊，用一般齒輪副重合度的計算方法比較困難，所以作者采取了重合度的另一種定義方法。首先介紹幾個概念：

齒輪作用角[5]:輪齒從開始嚙合到終止嚙合所轉過的角度, 用φ1表示。

周節圓心角:一個周節所對的圓心角，齒輪上不同圓(Ri)其周節(pi)是不同的,但是所有不同周節(pi)所對圓心角都是相同的[6],用φ表示,即

φ=2π/z

(16)

重合度定義為:齒輪作用角φ1與周節圓心角φ之比[6]。即:

(17)

周節圓心角與齒輪作用角的示意圖如圖7所示。

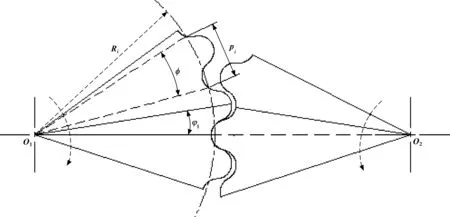
圖7 周節圓心角與齒輪作用角

因此，可以得到以下方程:

(18)

方程(18)表明：弧齒線擺線圓柱齒輪的端面重合度是常數,其值0.5。弧齒線擺線圓柱齒輪的軸向重合度εβ可以按弧線圓柱齒輪的軸向重合度[7]計算：

(19)

由式(18)和式(19)可以得到：

(20)

為了確保齒輪傳動可以持續和平穩,因此ε≥1,方程(20)重寫為:

RZ≤(B2+m2π2)/(4πm)

(21)

如方程(21)所示，增加B值或降低值RZ可以達到增加重合度ε值的目的。然而，如果RZ太小，則會導致正常的齒輪兩端法向厚度太薄，使得齒輪抗彎強度變弱[8]。如果RZ過大，弧齒軌跡與直線相似，不能體現弧齒的優點，而且可能會使重合度小于1。此外，RZ的值通常大于B值的一半，因此RZ值的范圍可以表示為:

B/2≤RZ≤(B2+m2π2)/(4πm)

2 弧齒線擺線圓柱齒輪副受力分析

由工業經驗和實驗室實驗數據可知，兩個高應力區域通常是漸開線齒輪失效的根源。這兩個區域是齒輪的齒根和齒輪的接觸表面[9]。利用三維建模軟件SolidWorks對一組弧齒線擺線圓柱齒輪副及漸開線直齒圓柱齒輪副進行齒面接觸受力分析。選定弧齒線擺線圓柱齒輪副的幾個參數：

(1)模數m為4 mm;

(2)小齒輪齒數z1為24;

(3)大齒輪齒數z2為48;

(4)齒輪寬度B為40 mm;

(5)齒線RZ半徑分別為24、26、30、32、34 mm;

(6)齒輪材料為合金鋼。

并添加約束，施加同樣大小的傳動轉矩1 000 N·m，在外界條件相同的情況下，對齒輪嚙合面進行接觸面選擇，然后劃分網格，最后進行受力分析。漸開線直齒齒輪副傳動采用同樣參數及步驟進行比較。RZ=34 mm時的弧齒線擺線圓柱齒輪副的應力圖如圖8所示，漸開線直齒圓柱齒輪副應力圖如圖9所示。在接觸齒側的彎曲應力被認為是拉應力，而對齒側的彎曲應力則被認為是壓應力。其余弧齒線半徑的應力數值結果統計如表1所示。

圖8 RZ=34 mm的弧齒線擺線圓柱齒輪副靜應力分析

圖9 直齒圓柱齒輪副靜應力分析

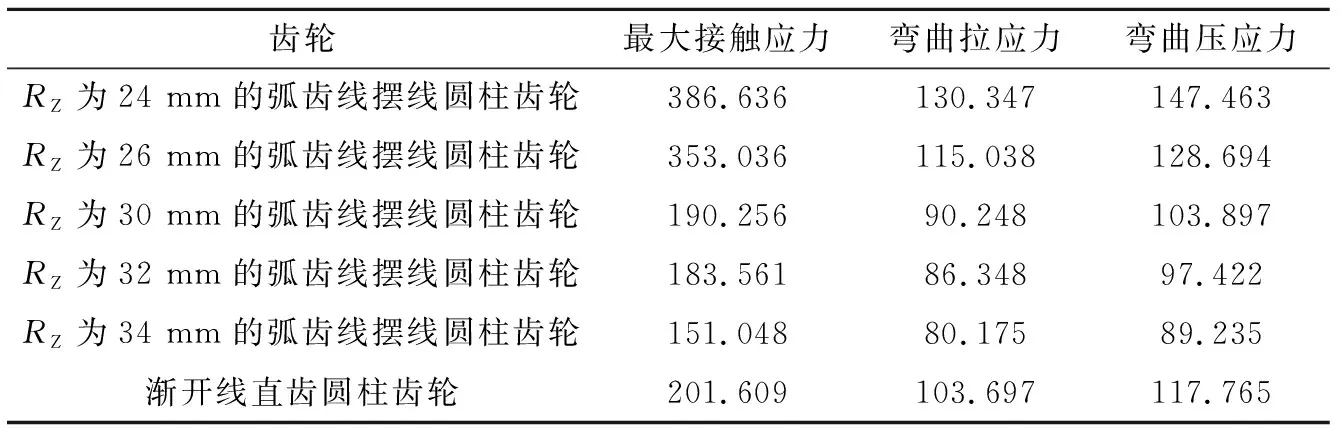
表1 靜應力有限元分析結果MPa

3 結論

以上闡述了弧齒線擺線圓柱齒輪的基本參數并利用有限元分析法對其齒面接觸應力和齒根彎曲應力進行了分析，可以得出以下結論:

(1)弧齒線擺線圓柱齒輪的接觸應力及彎曲應力隨著弧齒線半徑RZ的增大而逐漸減小。

(2)與漸開線直齒輪相比，當RZ為30、32、34 mm時(當弧齒線半徑RZ大于34 mm時，齒輪副重合度小于1，無法正常傳動，故未考慮RZ大于34 mm的情況)，在其他條件相同情況下，弧齒線擺線圓柱齒輪的最大接觸應力分別減少了5.63%、8.94%、25.07%，弧齒線半徑RZ越大，減小的百分比也越大。

(3)與漸開線齒輪相比，RZ為30、32、34 mm時，弧齒線擺線圓柱齒輪的齒根彎曲拉應力分別比漸開線齒輪低12.97%、16.06%、23.52%，齒根彎曲壓應力分別降低了11.12%、17.22%、24.14%。弧齒線半徑RZ越大，減小的百分比也越大。

(4)在保證齒輪副傳動重合度大于1的情況下，弧齒線RZ取值在0.75B～0.85B內時，與漸開線圓柱齒輪相比，弧齒線擺線圓柱齒輪具有更小的齒面接觸應力與齒根彎曲應力，具有比較好的接觸疲勞強度、彎曲疲勞強度和更長的使用壽命。