數學期望在工業企業經濟決策中的應用研究
劉昕琪
(江西財經大學, 江西 南昌 330013)
引言
隨著工業經濟的發展,工業企業經濟決策的科學性在企業發展過程中至關重要。工業經濟的發展依賴于對自然資源的占有和有效配置,以何種批量進行工業生產、投資何種機器設備等問題是工業企業經常面臨的經濟決策問題。數學期望作為一種科學的工具,通過相關理論知識將經濟問題量化為數學問題,能夠大大提高工業經濟決策的科學性與高效性。
1 數學期望的概念
數學期望是指在實驗中每種可能的結果與其相應的概率相乘的總和,是一種最基本的數學特征,反應了隨機變量的平均取值狀況。數學期望通過對每次實驗中的隨機變量進行相關計算,用統計學與概率論的思維來描述隨機變量的相關特征。
2 數學期望與工業企業經濟決策的關系
2.1 數學期望提高工業企業經濟決策的效率
工業企業的發展與工業企業管理者是否做出科學的決策息息相關。當工業企業管理者處于復雜環境背景下,數學期望的相關理論能夠幫助企業管理者將經濟問題來量化分析,通過一系列的數學計算,得出不同環境下的不同結果,并以計算結果作為決策標準,從而快速、高效、科學地解決復雜多樣的經濟問題。計算器、計算機等設備的使用更是加快了經濟問題的處理效率。可見,數學期望通過量化分析經濟問題,在保障決策科學性與準確的同時,大大提高了工業企業在復雜環境背景下經濟決策的效率。
2.2 數學期望提高了工業企業經濟決策的科學性
通過社會生活經驗總結出的理論知識在實踐中的應用,在一定程度上推動了人類對客觀世界的認知和改造,數學正是一種通過分析事物間的客觀規律來解決實踐中具體問題的科學、高效、準確的工具。在經營管理活動中,工業企業管理者有時是用感性的思維來分析問題,進行經濟決策時難免缺乏科學的理論指導,這使得不科學、不合理的執行結果在決策后時常發生,存在偏差或錯誤的決策結果嚴重影響了工業企業的正常經營。而數學期望的相關理論知識在工業企業經濟決策中的應用,能夠幫助管理者用科學、嚴謹的邏輯思維量化處理復雜的經濟決策問題,從而使管理者能夠做出科學的決策行為,大大提高工業企業經濟決策的科學性。
3 數學期望在工業企業經濟決策中的應用步驟
一般而言,數學期望在工業企業進行經濟決策時,可以按照以下步驟應用:
3.1 確定經濟決策的目標
確定經濟決策的目標,是工業企業管理層運用數學期望進行經濟決策的第一步。通過科學的篩選,以及綜合考慮多方面因素,使企業管理層能夠在特定條件與有效資源的約束下,做出可供選擇的多種方案。
3.2 計算影響因素的概率
在多種備選方案中,工業企業管理層應該全面、系統地分析對經濟決策具有影響作用的各種可控因素與不可控因素,在綜合分析各種影響因素的基礎上,運用數學期望方法計算出各種因素的概率,從而為下一步驟的計算提供數據支持。
3.3 計算企業預期收益值
在確定了不可控因素與可控因素等各類因素的發生概率后,工業企業管理者應依據統計學方法來計算企業收益值,并將該預期收益值與相應的概率對應。
3.4 選擇最優決策方案
首先,工業企業應以預期受益值與對應的概率為數據材料,根據數學期望的計算方法,計算出不同方案的數學期望,并以數學期望的大小作為決策標準,從而選在出最優的決策方案,提高工業企業的管理效率[1]。
4 數學期望在工業企業經濟決策中的應用案例
4.1 數學期望在工業企業最佳生產批量決策中的應用
最佳生產批量是指企業在成批生產中,使與之相關的生產費用最低的生產批量。工業企業在生產過程中,往往會遇到分幾批進行生產、每批生產產品多少個是最經濟合理的決策問題。以最佳生產批量進行生產,能夠幫助企業付出最小的生產成本或收取最大的經營利潤。數學期望在工業企業經濟決策中的應用,能夠幫助企業有效解決最佳生產批量這樣的決策經濟問題,期望利潤是常用的比較指標。
例如:在進行明年生產量決策時,某工業企業通過分析以往的生產資料及市場銷售情況,預測出市場銷路差、中、好的概率分別為 0.2、0.5、0.3,大、中、小的生產批量分別用A、B、C表示。通過市場經驗,明年銷路狀況與生產批量的關系如下表1所示。
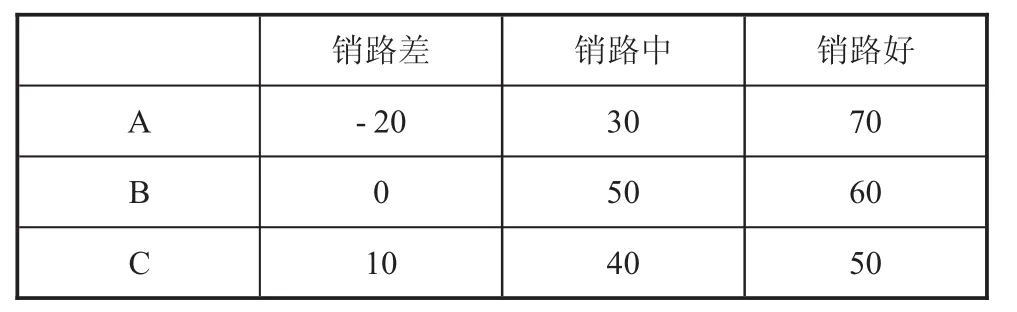
表1 A,B,C三者在不同銷路狀況的利潤表 萬元
通過分析,可以用數學期望法確定最佳生產批量,以預期利潤P的大小作為決策標準中。
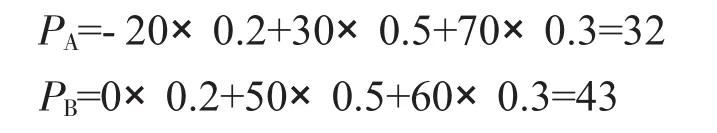
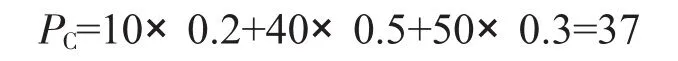
由于PB>PC>PA,生產批量B是該工業企業的最佳生產批量。
4.2 數學期望在工業企業投資決策中的應用
機器設備作為經營性長期資產,是工業企業發展的物質基礎,機器設備更新換代是工業企業一項重要的投資決策。工業企業在發展過程中,往往會遇到對機器設備購置或維修等多種提高產能的投資決策方案。通過數學期望方法,管理者能夠在綜合各種可預見因素與不可預見因素的前提下,從各種方案中得到期望值最大的決策方案,為工業企業的發展做出最優投資決策[2]。
例如:某工業企業需要一臺大型機床,企業管理者通過對市場上的a、b兩種機床進行調研,了解到兩種機床在相同環境下的次品數分別為c、d,通過分析長期產能表現,可得到c、d兩種機床的次品個數及概率為如表2、3所示。

表2 c種機床的次品個數及概率

表3 d種機床的次品個數及概率
通過分析,可以運用數學期望來分別計算兩類機床的次品率,將購置次品率E低的機床作為最優決策方案。
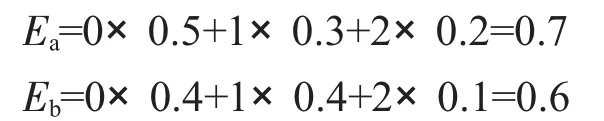
由于Ea

