模糊函數(shù)主脊切面特征提取的灰狼優(yōu)化方法

陳 磊 普運(yùn)偉 陳明偉 王 凌

1(昆明理工大學(xué)信息工程與自動化學(xué)院 云南 昆明 650504)2(昆明理工大學(xué)計(jì)算中心 云南 昆明 650500)

0 引 言

在現(xiàn)代戰(zhàn)爭中，各種新型復(fù)雜體制雷達(dá)逐漸在對抗雙方的電子裝備中占據(jù)了主流，電子威脅環(huán)境中的信號密度也已達(dá)到了每秒百萬個(gè)脈沖。電磁環(huán)境的惡化，致使基于傳統(tǒng)五參數(shù)—到達(dá)時(shí)間(TOA)、載波頻率(RF)、脈沖寬度(PW)、脈沖幅度(PA)以及到達(dá)角(DOA)的分選方法效果大大降低[1]。因此，補(bǔ)充新的針對各種新型復(fù)雜體制雷達(dá)輻射源信號分選的有效特征參數(shù)，以滿足當(dāng)前電子對抗領(lǐng)域?qū)Ψ诌x技術(shù)更高的要求，成為當(dāng)務(wù)之急。

脈內(nèi)特征是當(dāng)前分選特征中的研究熱點(diǎn)。它從信號自身結(jié)構(gòu)的角度出發(fā)，研究不同信號間的本質(zhì)差別，如瞬時(shí)頻率特征[2]、小波分析提取脈內(nèi)特征[3]、熵特征[4]、相像系數(shù)[5-6]、時(shí)頻原子特征[7]、脈沖相位線性度特征[8]、雷達(dá)指紋個(gè)體特征[9-10]等。但這些方法基本上只適用于幾種特定類型的雷達(dá)信號，沒有從本質(zhì)和普遍意義上系統(tǒng)的研究信號特征對于信號分選的意義。為此，在文獻(xiàn)[1]中，普運(yùn)偉博士首次將信號的模糊函數(shù)能量分布特征應(yīng)用于雷達(dá)輻射源信號的分選中，該方法首先提取到模糊函數(shù)主脊AFMR(Ambiguity Function Main Ridge)的切面，然后從圖像學(xué)的角度構(gòu)建主脊方向、切面的重心和切面的慣性半徑三個(gè)特征參數(shù)來描述不同輻射源信號的AFMR切面。仿真實(shí)驗(yàn)表明，所提特征即使在低信噪比下依然能夠很好地將六種雷達(dá)輻射源信號分開。但是，文獻(xiàn)[1]的提取方法初步解決了模糊函數(shù)主脊切面特征的提取問題，其提取效率與精度還有待提高。近年來新出現(xiàn)的一些群智能優(yōu)化算法憑借自身優(yōu)秀的算法設(shè)計(jì)，對大多數(shù)實(shí)際工程問題具有較好的全局啟發(fā)式尋優(yōu)能力，且較快的收斂速度大大提高了工作的效率。因此采用更有效的群智能搜索算法指導(dǎo)AFMR切面的搜索方向，進(jìn)一步提高AFMR切面搜索的效率，已被證明是一種可行方案，例如：PSO方法[11]和GA方法[12]。

為了進(jìn)一步提高搜索AFMR切面的搜索效率，本文構(gòu)建了一種新的改進(jìn)灰狼算法用于提取AFMR切面特征。為驗(yàn)證該算法的可行性與有效性，將所提方法用于提取六種典型復(fù)雜體制雷達(dá)輻射源信號的AFMR切面特征，并且與上述兩種智能搜索方法[11-12]進(jìn)行對比實(shí)驗(yàn)。實(shí)驗(yàn)結(jié)果表明，本文方法具有更高的搜索效率與準(zhǔn)確率，且在低信噪比下有更好的抗噪性能。

1 模糊函數(shù)主脊切面特征

任意窄帶雷達(dá)信號的模糊函數(shù)定義為：

(1)

式中，s*(t)為s(t)的共軛，τ為時(shí)延，ξ為頻移。該公式表明，信號的模糊函數(shù)實(shí)際上是信號在時(shí)延τ和頻移ξ平面上的聯(lián)合二維時(shí)頻表示。

Akay等定義了分?jǐn)?shù)自相關(guān)運(yùn)算，并指出其與模糊函數(shù)具有如下關(guān)系[13]：

?Cα(s,s)」(ρ)=χs(ρcosα,ρsinα)

(2)

式中:Cα是旋轉(zhuǎn)角為α的分?jǐn)?shù)域uα上的分?jǐn)?shù)自相關(guān)算子，ρ為uα域的徑向距離。該公式表明，旋轉(zhuǎn)角為α的分?jǐn)?shù)域的自相關(guān)等價(jià)于該分?jǐn)?shù)域上模糊函數(shù)的徑向切片。因此，利用分?jǐn)?shù)傅里葉變換的快速離散方法，便可計(jì)算模糊函數(shù)任意過原點(diǎn)的徑向切面。

文獻(xiàn)[1]中構(gòu)建了如下檢測量：

(3)

根據(jù)檢測量RS(a)，可得到AFMR的三個(gè)特征向量：

(4)

(5)

(6)

2 基于自適應(yīng)灰狼算法的AFMR切面智能搜索方法

灰狼優(yōu)化算法GWO(Grey Wolf Optimization)是受自然界中灰狼種群捕食行為的啟發(fā)而提出的一種新型智能優(yōu)化算法[14]。灰狼算法具有較強(qiáng)的全局搜索能力、簡單易于實(shí)現(xiàn)的結(jié)構(gòu)設(shè)計(jì)和較少的可調(diào)參數(shù)。因此，灰狼算法在PI控制器參數(shù)優(yōu)化[15]、多層傳感器訓(xùn)練[16]、電力潮流優(yōu)化[17]、多輸入多輸出電力系統(tǒng)[18]和K均值聚類優(yōu)化[19]等領(lǐng)域中被廣泛應(yīng)用。

在標(biāo)準(zhǔn)灰狼算法中，灰狼種群按照等級的高低劃分為四等，即α、β、δ和ω。第一等的頭狼稱為α，是種群的領(lǐng)導(dǎo)者與管理者；第二等狼稱為β，是頭狼α的助手，當(dāng)狼群中的頭狼α不在時(shí)，可以由它頂替；第三等狼稱為δ，是頭狼α和次等狼β的執(zhí)行者；最低等的狼稱為ω，它們則跟隨前三頭狼，負(fù)責(zé)平衡種群的內(nèi)部關(guān)系。每一只狼不斷地更新自己的位置來逐漸接近獵物，直到最終包圍找到獵物，即灰狼算法找到了最優(yōu)解。每只狼的位置更新公式如下：

(7)

(8)

(9)

(10)

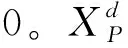
在實(shí)際的捕獵過程中，狼群并不知道獵物的具體位置，但是可以認(rèn)為α、β和δ三頭狼(保存的前三個(gè)歷史最優(yōu)值)是最接近獵物的。因此，其他狼是根據(jù)這三頭狼來大體判斷獵物的位置并確定自己的最終位置。

(11)

(12)

(13)

(14)

式(11)、式(12)和式(13)為保存的三個(gè)歷史最優(yōu)位置，式(14)表示的是灰狼個(gè)體的最終位置，即獵物所在的地方。

為了進(jìn)一步提高AFMR切面的搜索效率，本文構(gòu)建了一種新型自適應(yīng)灰狼算法用于搜索AFMR切面。具體步驟包括均勻初始化、新型非線性收斂因子和自適應(yīng)種群更新策略等，其中選取最大RS(a)值的切面作為AFMR切面。

2.1 均勻初始化

在標(biāo)準(zhǔn)灰狼算法中，采用的是簡單的隨機(jī)初始化策略，其缺點(diǎn)就是一開始所有的初始解可能分布不均勻，而使算法收斂到局部最優(yōu)解。而通過研究當(dāng)前幾種常見的灰狼算法初始化改進(jìn)策略可以發(fā)現(xiàn)，人們剛開始利用Logistic混沌映射模型產(chǎn)生初始種群，但隨后發(fā)現(xiàn)這種方法在兩個(gè)特定的區(qū)域內(nèi)取值概率偏高，對初值設(shè)置敏感，有一定的遍歷不均勻性[20]。后來更多地采用兩種改進(jìn)型的混沌映射模型—Tent映射與Cat映射，這可以在一定程度上進(jìn)一步改進(jìn)初始化的效果[21-22]。或者，可以采用對立學(xué)習(xí)初始化方法或用此種方法與上述混沌映射模型相結(jié)合來初始化種群[23]。上述幾種混沌映射模型可以在一定程度上改善隨機(jī)初始化方法均勻性較差的缺點(diǎn)，但這些模型仍受到迭代初值的影響，導(dǎo)致在某一區(qū)域內(nèi)取值概率偏高。而對立學(xué)習(xí)初始化方法的使用，會產(chǎn)生雙倍的種群，而且還需要對兩倍種群的個(gè)體計(jì)算適應(yīng)度值，最后擇優(yōu)選取個(gè)體，這對于一些高維復(fù)雜的優(yōu)化問題，會增加算法的復(fù)雜度，降低算法的效率。對于一些相對簡單且低維度的優(yōu)化問題，采用均勻初始化策略，可以在不增加算法復(fù)雜度和不降低算法效率的前提下，有效地保證了初始種群在搜索空間內(nèi)均勻分布，且沒有重疊點(diǎn)。在本文方法中，初始灰狼種群選取的是自變量取值范圍(-pi/2，pi/2)內(nèi)的20個(gè)等間隔值，調(diào)整分布的間隔距離使候選解盡可能地覆蓋所有可行解，為算法的全局搜索能力奠定良好的基礎(chǔ)。

圖1-圖3分別為隨機(jī)初始化方法、Tent映射初始化方法和均勻初始化方法初始化灰狼種群的個(gè)體分布示意圖。

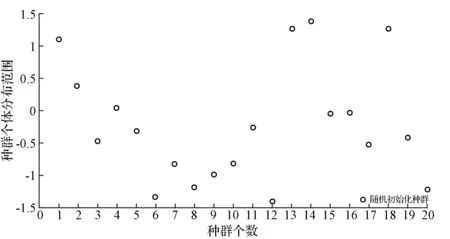
圖1 隨機(jī)初始化灰狼種群的個(gè)體分布示意圖

圖2 Tent映射初始化灰狼種群的個(gè)體分布示意圖

圖3 均勻初始化灰狼種群的個(gè)體分布示意圖

2.2 改進(jìn)的非線性收斂因子

一般來說，一種性能優(yōu)秀的群智能優(yōu)化算法應(yīng)該要達(dá)到前期較強(qiáng)的探索能力與后期較強(qiáng)的開發(fā)能力之間的平衡。否則，容易使算法陷入局部最優(yōu)或者早熟收斂。

在標(biāo)準(zhǔn)GWO算法中，其探索能力與開發(fā)能力之間的協(xié)調(diào)主要取決于收斂因子a。a的值是隨迭代次數(shù)的增加從2線性遞減到0，而在大多數(shù)情況下實(shí)際的優(yōu)化搜索過程卻是非線性的。因此，本文提出一種新的非線性收斂因子更新公式：

(15)

式中:l為當(dāng)前迭代次數(shù)；lmax為最大迭代次數(shù)，afinal為終止值，ainitial為初始值，本文取值為2.5和0；k為非線性調(diào)節(jié)系數(shù)，其值越大則a的非線性遞減曲線越彎曲，本文取值為3。該公式一方面使a在算法初期的值適當(dāng)提高，對應(yīng)于灰狼種群擴(kuò)大搜索范圍，有利于找到全局最優(yōu)解；同時(shí)，a的遞減曲線衰減快，防止a的取值始終過高，影響后期的局部搜索。另一方面，在算法后期，收斂因子a的取值適當(dāng)?shù)剡M(jìn)一步減小，對應(yīng)于灰狼種群縮小搜索范圍，有利于精細(xì)化搜索和提高解的精度，但遞減曲線衰減慢，保證了種群有足夠的時(shí)間進(jìn)行局部搜索。a的非線性遞減圖如圖4所示。

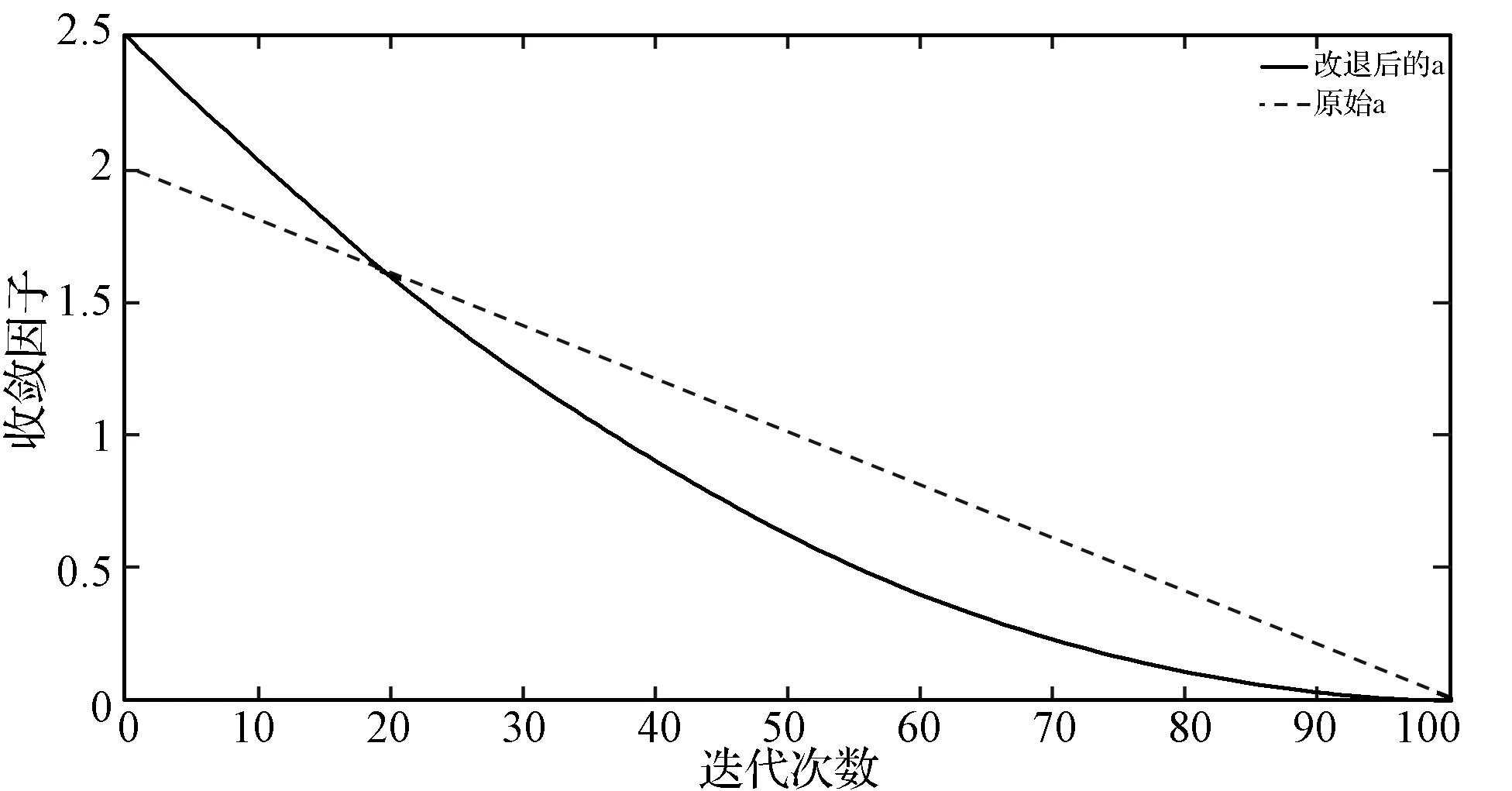
圖4 收斂因子對比圖

2.3 自適應(yīng)種群更新策略

在標(biāo)準(zhǔn)灰狼算法中，位置更新方程表現(xiàn)出α、β和δ具有同等重要性，這樣就沒有充分體現(xiàn)出灰狼算法中的等級制度思想，忽略了α狼的領(lǐng)導(dǎo)地位與作為最優(yōu)解應(yīng)該所占有的比例大小，從而造成算法無法始終保證在最優(yōu)解周圍進(jìn)行搜索，降低了算法的收斂效率。

本文提出一種新的自適應(yīng)調(diào)整策略，是將遺傳算法中遺傳與變異的思想引入到改進(jìn)的灰狼算法中，使新個(gè)體學(xué)習(xí)三頭狼的概率在不同的情況下采用不同的比重。具體方法是：首先比較當(dāng)前個(gè)體的適應(yīng)度值fi與灰狼種群的平均適應(yīng)度值favg。如果前者大于后者，則說明該個(gè)體較為優(yōu)秀，應(yīng)該繼續(xù)多向最優(yōu)的個(gè)體學(xué)習(xí)，即適當(dāng)增加學(xué)習(xí)種群中優(yōu)秀個(gè)體的概率，保證下一代種群能夠遺傳到優(yōu)良的基因，提高收斂的效率；如果前者小于后者，則說明該個(gè)體較差，進(jìn)化速度減緩，優(yōu)秀個(gè)體很有可能陷入局部最優(yōu)，這時(shí)要適當(dāng)增加自身變異的概率，減少學(xué)習(xí)優(yōu)秀個(gè)體的概率，盡可能跳出局部最優(yōu)，具體公式如下：

(16)

至此，基于自適應(yīng)改進(jìn)灰狼算法的AFMR切面智能搜索方法的具體步驟如下：

Step1以一定的采樣頻率fs對信號s(t)進(jìn)行離散化，得到信號s(n)；

Step2以有理分式M/N(M=1 024)對s(n)進(jìn)行重采樣，以使各信號保持相同的長度M；

Step3將自變量的取值范圍(-pi/2，pi/2)平均分成 20份，去掉兩邊端點(diǎn)極值中的一個(gè)后，取剩余的端點(diǎn)值作為初始灰狼種群；

Step4以RS(a)作為目標(biāo)函數(shù)，采用改進(jìn)的自適應(yīng)灰狼算法搜索AFMR切面；

Step5迭代終止，計(jì)算AFMR切面的三個(gè)特征值。

3 實(shí)驗(yàn)結(jié)果及分析

選取二頻率編碼(BFSK)、二相編碼(BPSK)、四相編碼(QPSK)、M偽隨機(jī)序列(M-SEQ)、線性調(diào)頻信號(LFM)和常規(guī)信號(CON)六種典型信號進(jìn)行實(shí)驗(yàn)。四種搜索方案的信號參數(shù)保持與文獻(xiàn)[1]相同，仿真平臺為MATLAB R2014a。另外，為便于比較并兼顧搜索速度和效率，三種智能搜索算法的運(yùn)行參數(shù)統(tǒng)一為：種群數(shù)量為20，最大迭代次數(shù)為100，當(dāng)適應(yīng)度值的相對變化幅度小于或等于0.001或迭代次數(shù)大于等于100代時(shí)迭代終止。各實(shí)驗(yàn)分別進(jìn)行100次蒙特卡洛隨機(jī)測試。

實(shí)驗(yàn)一 保持SNR為20 dB，每類信號各隨機(jī)產(chǎn)生100個(gè)不同初相的測試樣本，分別利用本文方法和窮舉法[1]、PSO方法[11]和GA方法[12]提取各信號樣本的AFMR切面特征并比較其搜索耗時(shí)、RS(a)值的大小及平均收斂終止代數(shù)。其中，搜索耗時(shí)是指提取100個(gè)信號切面特征的平均耗時(shí)，計(jì)時(shí)用函數(shù)tic和toc來統(tǒng)計(jì)。搜索耗時(shí)、平均收斂終止代數(shù)及RS(a)值的大小分別列于表1、表2和表3。圖5、圖6和圖7對比性地給出了某一次三種智能搜索方法搜索BPSK、QPSK和M-SEQ三種信號的迭代收斂情況。圖8-圖10為某一次上述四種方法下所提取的BPSK、QPSK和M-SEQ三種信號的AFMR切面。

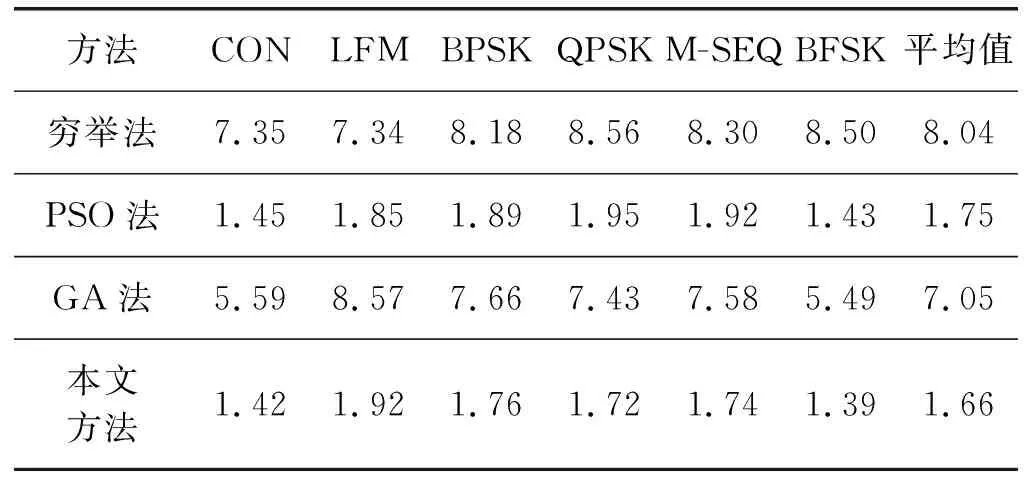
表1 AFMR切面特征提取耗時(shí)比較 s

表2 三種智能搜索算法平均收斂終止代數(shù)比較

表3 AFMR切面適應(yīng)度值比較

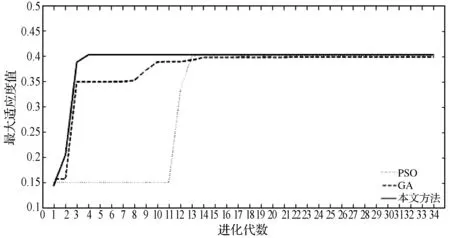
圖5 SNR=20 dB時(shí)，BPSK的優(yōu)化過程

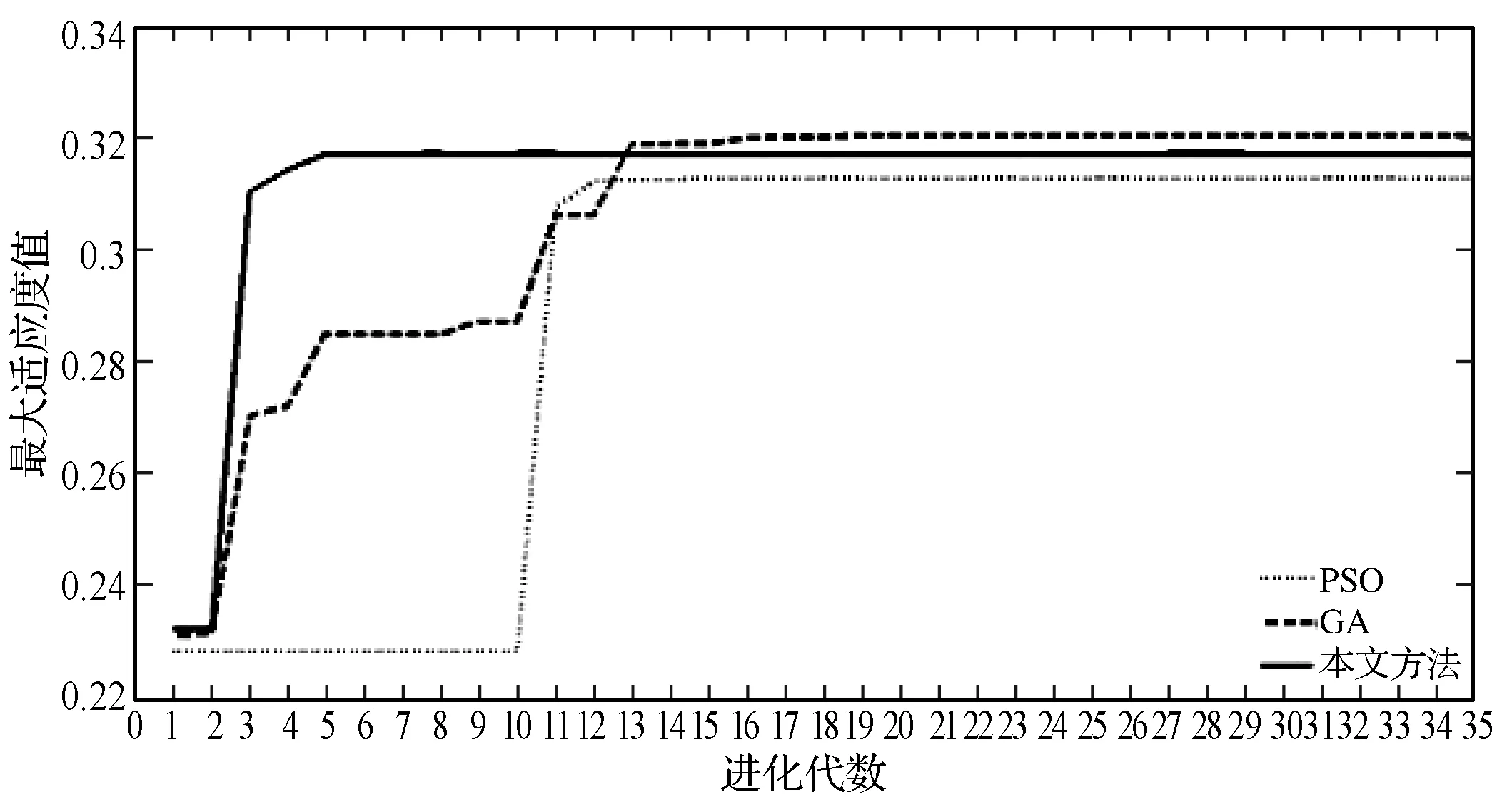
圖6 SNR=20 dB時(shí)，M-SEQ的優(yōu)化過程

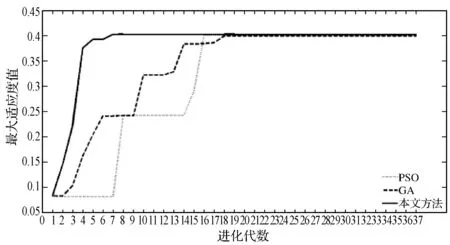
圖7 SNR=20 dB時(shí)，QPSK的優(yōu)化過程

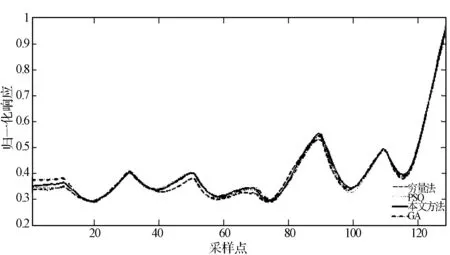
圖8 SNR=20 dB時(shí)，四種方法下BPSK信號AFMR截面

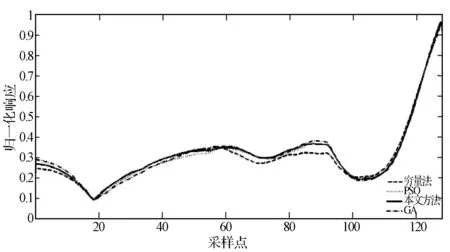
圖9 SNR=20 dB時(shí)，四種方法下M-SEQ信號AFMR截面

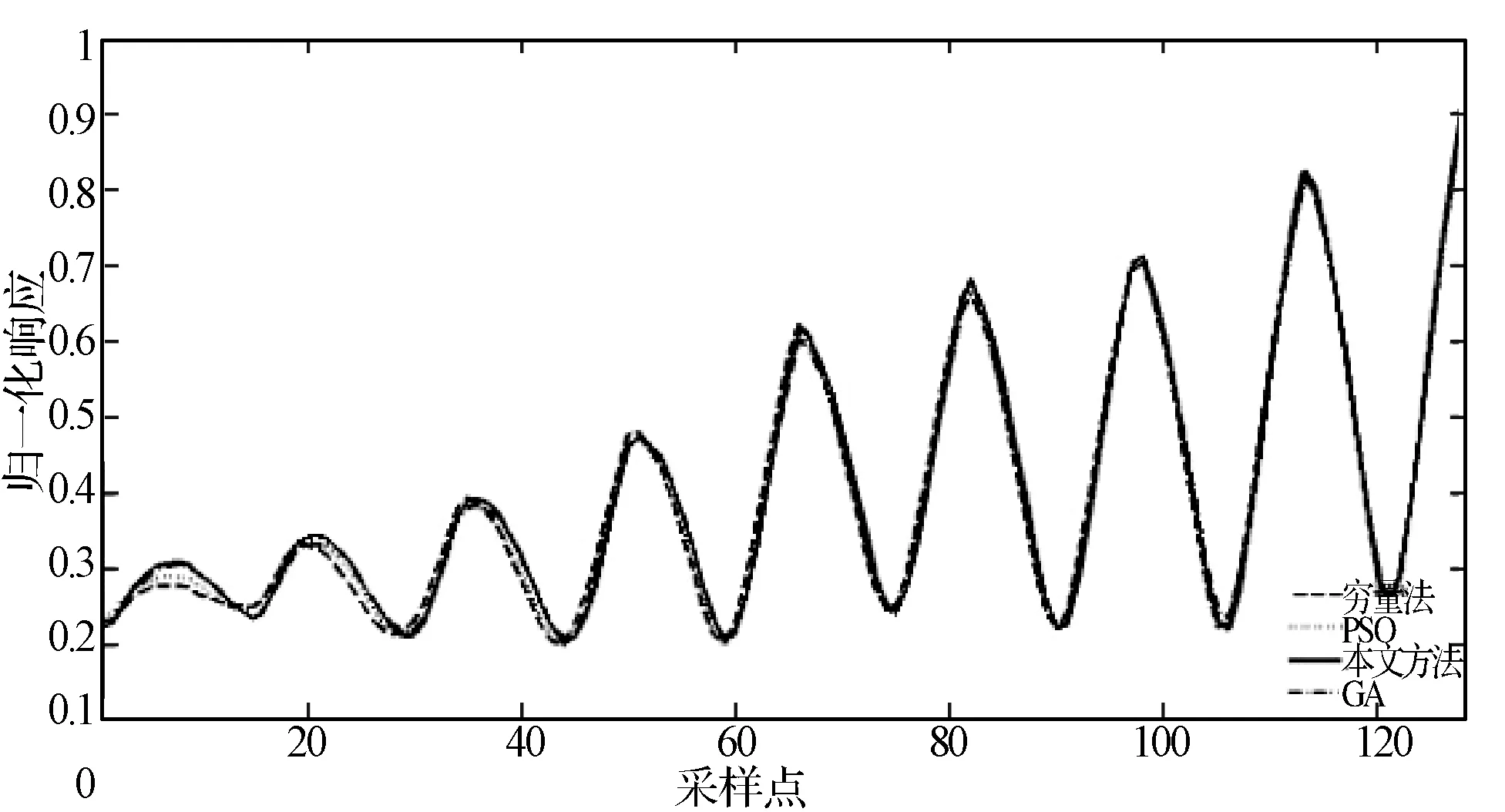
圖10 SNR=20 dB時(shí)，四種方法下QPSK信號AFMR截面

由圖5至圖7可見，本文方法能在較少的迭代次數(shù)內(nèi)快速搜索到全局最優(yōu)解，且相比于其他兩種智能搜索方法沒有出現(xiàn)收斂曲線中的“小平臺”——陷入局部最優(yōu)的情況，顯示出了較好的全局探索能力。圖8至圖10顯示了本文方法在快速收斂的同時(shí)，搜索到了更大的主脊切面，其局部精確搜索能力具有一定優(yōu)勢。

此外，由表1不難看出，三種智能搜索方法和窮舉法相比，平均計(jì)算耗時(shí)已大大減小，但本文方法是減小幅度最大的；其平均計(jì)算耗時(shí)僅為1.66 s，分別比其他的兩種智能搜索方法降低76.5%和5.1%。通過表2可以進(jìn)一步看出，本文方法對六種信號的平均收斂代數(shù)僅為35.5代，低于PSO法的37.6代，也低于GA法的39.9代。另外，表3的結(jié)果表明，本文方法搜索到的RS(a)值均大于窮舉法搜索到的RS(a)值，且與其他兩種智能搜索方法相比，精確度的改進(jìn)率分別為2.63%和0.73%，其局部開發(fā)能力也具有一定的優(yōu)勢。

實(shí)驗(yàn)二 為進(jìn)一步說明本文方法的抗噪性能，保持SNR為0、6、12和20 dB，每類信號同樣各產(chǎn)生100個(gè)隨機(jī)樣本，分別組成SNR固定的4個(gè)測試信號集。利用實(shí)驗(yàn)一的方法，統(tǒng)計(jì)各SNR情況下的三種智能搜索方法搜索各信號的搜索成功率，這里搜索成功的含義是指提取的三個(gè)AFMR切面特征均位于E±3δ范圍之內(nèi)，其中E和δ分別為文獻(xiàn)[1]中的某AFMR切面特征的均值和標(biāo)準(zhǔn)差。結(jié)果如表4所示。

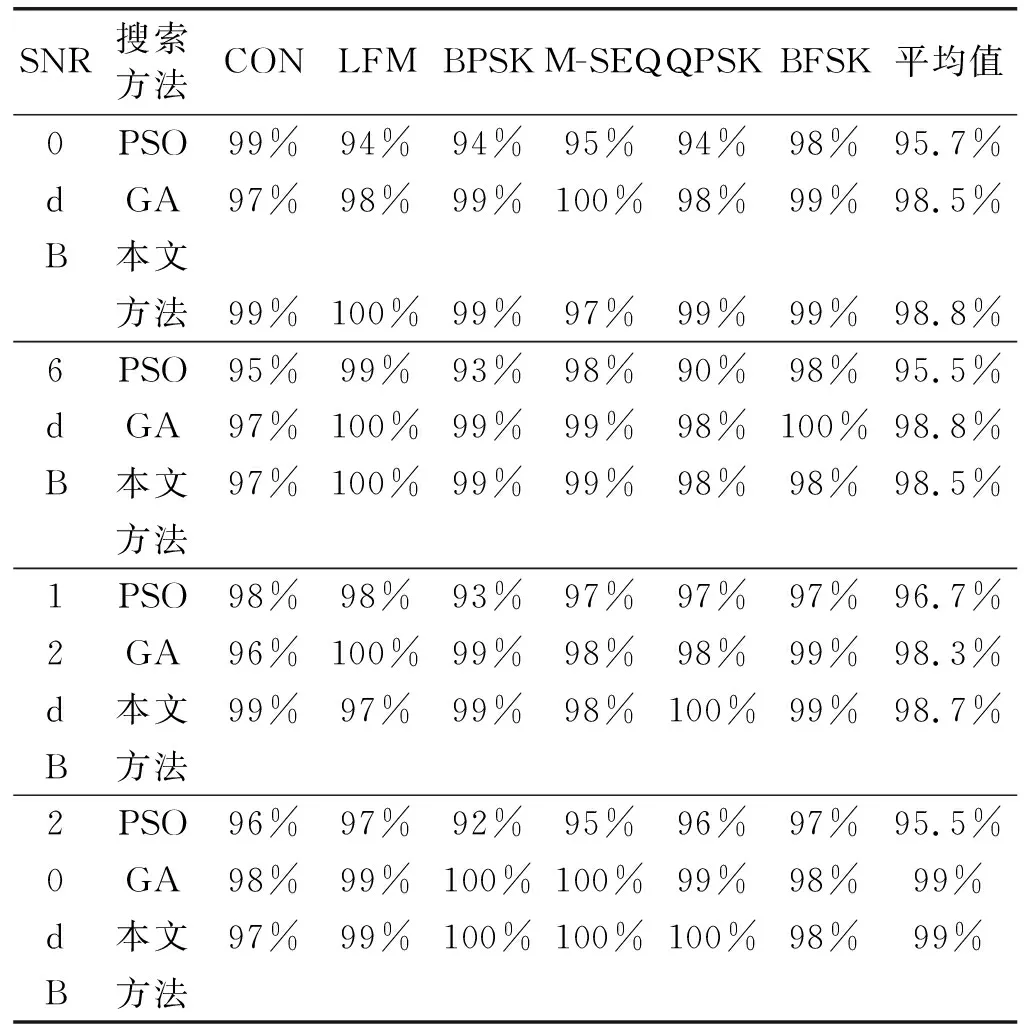
表4 SNR變化時(shí)各信號的搜索成功率

從表4的結(jié)果可知，本文方法在四種固定信噪比的情況下，對于大部分信號來說，具有三種搜索方法中較高的搜索成功率，分別為98.8%、98.5%、98.7%和99%，表現(xiàn)出了良好的穩(wěn)定性。同時(shí)，進(jìn)一步發(fā)現(xiàn)，本文方法在信噪比不低于0 dB的情況下，平均搜索成功率保持在98.8%左右，能以較高的概率提取到所需要的AFMR切面特征，表現(xiàn)出了較好的抗噪性能。

4 結(jié) 語

尋找并補(bǔ)充經(jīng)典五參數(shù)之外的有效特征將從根本上緩解當(dāng)今復(fù)雜體制雷達(dá)輻射源信號分選困難的現(xiàn)狀。從信號內(nèi)在結(jié)構(gòu)信息的角度，挖掘雷達(dá)輻射源信號本身的固有特征，AFMR切面特征顯示出了較好的信號分辨能力與抗噪聲性能，將有利于信號分選問題的解決。但傳統(tǒng)AFMR切面搜索方法效率較低，限制了其實(shí)際工程應(yīng)用。為了進(jìn)一步提高AFMR切面搜索效率，本文構(gòu)建了一種改進(jìn)型自適應(yīng)灰狼算法的AFMR切面特征快速提取新方法，并與其他兩種智能搜索方法在性能上進(jìn)行比較。實(shí)驗(yàn)結(jié)果表明，本文方法在三種智能搜索方法中具有較優(yōu)的搜索效率與搜索精度，且在低信噪比情況下，具有較優(yōu)的抗噪性能。如何進(jìn)一步優(yōu)化本文算法進(jìn)而設(shè)計(jì)更為高效的搜索方法將是下一步值得研究的工作。