基于免疫克隆選擇算法的爬升飛行方案優化設計

高 峰，李亞輝，師 嬌，趙 洪，馬奧家

（中國運載火箭技術研究院，北京，100076）

0 引 言

平飛俯沖擊頂彈道是目前先進無人飛行器的典型攻擊方式之一，可使飛行器從目標上方對較為薄弱的頂裝甲進行攻擊，增加毀傷效率。采用平飛俯沖擊頂彈道時，首先需要使飛行器爬升至一定高度，然后轉入定值高度平飛，滿足轉比條件時，按末制導律對目標進行俯沖攻擊。爬升段彈道即飛行器起控開始爬升直至進入平飛前的一段彈道，其任務是使飛行器能夠快速、穩定地爬升至平飛高度，并迅速地轉入平飛段飛行，是保證飛行器完成對目標攻擊的重要前提。由于飛行器在爬升段彈道的飛行過程中會受到爬升時間、爬升高度、可用攻角、導引頭框架角等諸多因素制約，既要求飛行器在短時間內快速爬升至一定高度，又不能在爬升過程中丟失目標，因此需要對其進行優化設計，以提高飛行器的爬升效率，縮短爬升段的飛行時間，盡快進入理想戰斗高度。為此，本文首先應用非均勻B樣條（Non-uniform B-spline，NUBS）對無人飛行器爬升段的飛行控制方案進行了參數化處理，然后基于免疫克隆選擇算法（Immune Clonal Selection Algorithm，ICSA）設計了爬升飛行方案優化流程，以爬升時間為主要優化目標進行了優化設計。

1 數學模型

1.1 問題描述

飛行器的爬升段彈道通常采用方案飛行，即按預定的飛行方案進行飛行，其中飛行方案是指設計彈道時所選定的某個運動參數隨時間的變化規律[1]。通過初步分析易知，爬升時飛行器的彈道傾角與速度越大，飛行器到達平飛高度所需要的時間越小。但在實際的飛行過程當中，爬升時的彈道傾角與速度將受到失速攻角、導引頭可用框架角等諸多因素的限制，且爬升時的彈道傾角越大，轉入平飛的過渡時間越長。因此，爬升段彈道設計是一類復雜的非線性問題。

飛行器爬升段彈道優化設計的實質就是對所采用的飛行方案進行優化，即尋求一組最優的運動參數變化規律，使飛行器在滿足各種約束條件的限制下，以最短時間爬升到指定高度轉入平飛。

1.2 飛行運動模型

平飛俯沖擊頂彈道的爬升段、平飛段以及末制導段是基于縱向平面內的彈道特征劃分的，因此本文爬升飛行方案的優化設計也基于縱向平面。飛行器縱向平面內的運動方程[1]為

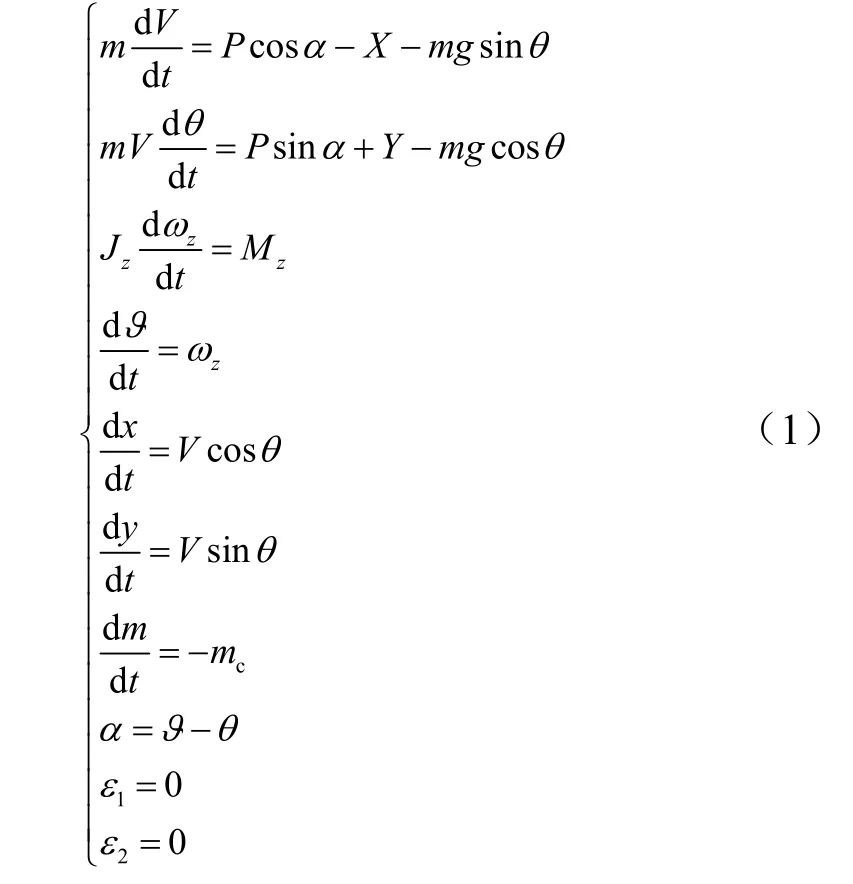
式中 m為質量；V為速度；t為時間；P為推力；α為攻角；X為阻力；g為重力加速度；θ為彈道傾角；Y為升力；為轉動慣量；zω為俯仰角速度；zM為俯仰力矩；?為俯仰角；x，y為飛行器質心位置坐標；為燃料質量秒流量；ε1，ε2為理想控制關系方程。

2 飛行方案參數化

爬升段飛行方案常用的運動參數控制規律包括俯仰角?變化規律、攻角α變化規律以及彈道傾角θ變化規律等。目前彈上的攻角傳感器與速度傾角傳感器的精度并不是很理想，且成本較高。因此出于采用成熟技術、控制成本的角度考慮，無人飛行器的飛行方案采用俯仰角?變化規律較為合適。式（1）中的理想控制關系式表示為

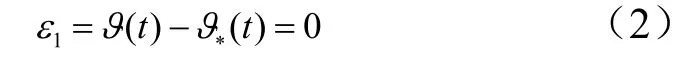
式中 ()t?為俯仰角?隨時間變化規律；()t??為給定的俯仰角?變化規律。為保證在優化過程中對其進行準確描述以使效果達到最優，本文并未采用傳統設計中常用的指數形式的變化規律，而是采用了計算機輔助幾何設計中常用的非均勻B樣條曲線[2,3]，其曲線方程可寫為

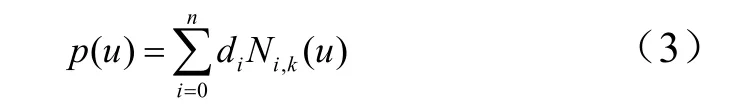
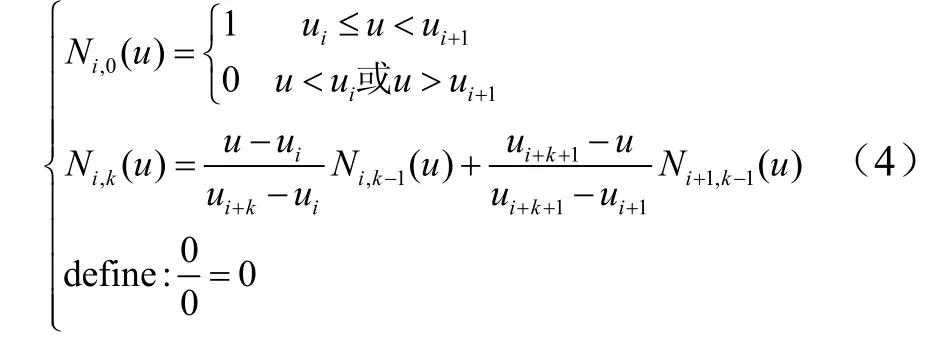
式中 lj為控制多邊形的各邊長，1,2,…,n)；L為總邊長，

這樣，通過NUBS將控制規律參數化，從而將對飛行方案優化轉化為對NUBS優化，優化設計變量為NUBS的控制頂點

3 飛行方案優化設計

3.1 約束條件

在飛行器爬升過程中，如果在飛行過程中超出了可用框架角的范圍，將導致導引頭碰框并丟失目標；如果超出了臨界攻角，將會導致飛行器升力急劇下降。因此，為保證飛行器在爬升段的正常飛行，應該對飛行過程中的框架角和攻角進行限定，約束條件為導引頭框架角為導引頭可用框架角）以及攻角為臨界攻角）。一般在彈道優化中多采用罰函數法將約束問題轉化為無約束優化問題進行考慮，但需要對懲罰因子進行設計。本文中根據罰函數法的基本原理，將約束條件轉化為多目標優化問題中的兩個目標1()gx和2()g x進行處理[4]，即：

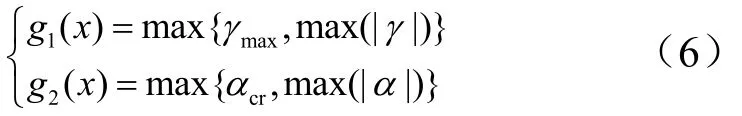
3.2 目標函數

飛行器爬升段的主要目的為爬升至指定高度，以及迅速完成爬升至平飛的過渡過程。因此，在爬升段結束時，飛行器應達到平飛高度，并滿足平飛初始狀態，一般主要指彈道傾角θ，在平飛時有lf0θ=。考慮到以上要求，本文目標函數取為飛行器爬升到平飛高度lfh后彈道傾角θ減小至0的所需時間T，綜合式（6），目標函數 ()fx為

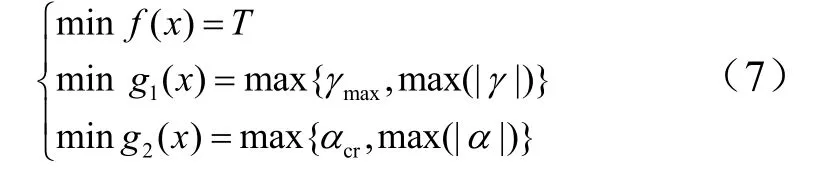
但應注意的是，雖然本文中將約束問題轉化為多目標優化問題來處理，但與一般多目標優化問題的區別是，轉化過來的目標函數在可行域內又退化成一個單目標優化問題 f(x)，此時有這樣最終得到的是最優解而不是向著最優 Pareto-前端逼近的最優解集。

3.3 優化算法設計

ICSA是基于人工免疫系統（Artificial Immune Systems，AIS）的基本原理而提出的一種進化算法[4]。ICSA在收斂速度和多樣性保持方面都有較好的效果，其核心步驟包括免疫克隆操作、免疫基因操作以及抗體更新操作等，其中免疫基因操作又包括克隆重組操作和克隆變異操作。

為提高優化效率，在本文的實際應用中，忽略了克隆重組操作。在克隆變異操作中，為防止算法出現類似于遺傳算法早熟的現象，同時也能根據自身適應度值調整搜索范圍，在本文中采用了將非一致性變異與自適應變異[5]相結合的方法。

在開始優化前，首先根據飛行力學模型進行初步彈道仿真，可有效縮小抗體向量的搜索空間，提高優化收斂速度。結合NUBS生成算法，將控制點作為抗體向量，得到基于ICSA的無人飛行器爬升飛行方案優化設計的步驟如圖1所示，具體如下：

a）初始化飛行力學模型，進行初步彈道仿真，確定抗體向量的搜索空間；

b）給定抗體群規模N、平均克隆規模R、最大迭代次數maxg 、隨機產生初代抗體群A；

c）用抗體向量所代表的控制頂點生成NUBS作為控制量，代入飛行器飛行力學模型進行解算，得到各抗體目標函數值；

d）根據抗體間親和力確定克隆規模，對抗體群A進行克隆操作，得到抗體群1A；

e）運用非一致性變異與自適應變異組合方式對抗體群1A進行免疫克隆變異操作，得到抗體群2A；

f）根據步驟c計算抗體群2A各抗體目標函數值，

進行克隆選擇操作，將抗體群2A劃分為支配抗體群和非支配抗體群 Anon；

g）根據nonA 的目標函數值求解各抗體適應度值，進行抗體群更新操作，將非支配抗體群nonA 擴充（）或縮小（nonNN＜）為抗體群3A（），其中nonN 與3N分別為nonA 與3A的抗體群規模；

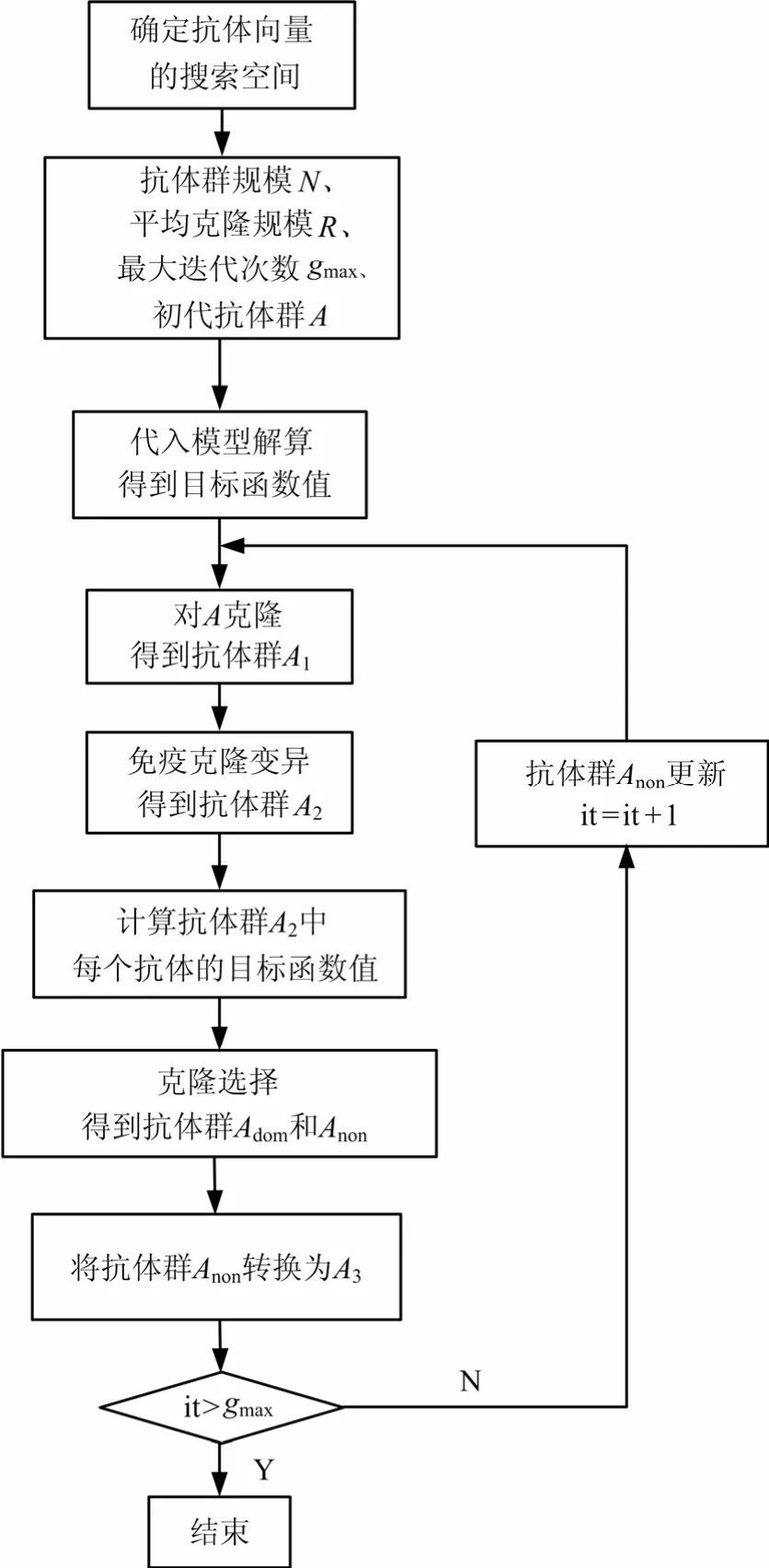
圖1 基于ICSA的爬升飛行方案優化設計步驟Fig.1 Procedure of Climbing Flight Scheme Optimal Design Based on ICSA

4 仿真分析

根據圖 1所示的優化設計步驟對無人飛行器的爬升飛行方案進行優化設計。在仿真過程中，將舵機簡化為比例環節，穩定回路由姿態自動駕駛儀和彈體組成；設定理想平飛高度為150 m；飛行器的初始狀態設定為：初始速度 16 m/s，初始射角 18°，啟控時間0.3 s，導引頭可用框架角限定為±25°，攻角限定條件設置為±15°；選用二次 NUBS，控制頂點id中，n=16；免疫克隆算法種群規模N=10，最大迭代次數爬升時間優化目標為不大于7 s；綜合目標函數：

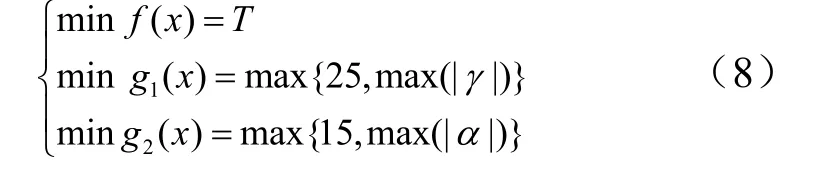
仿真結果如圖2～8所示。

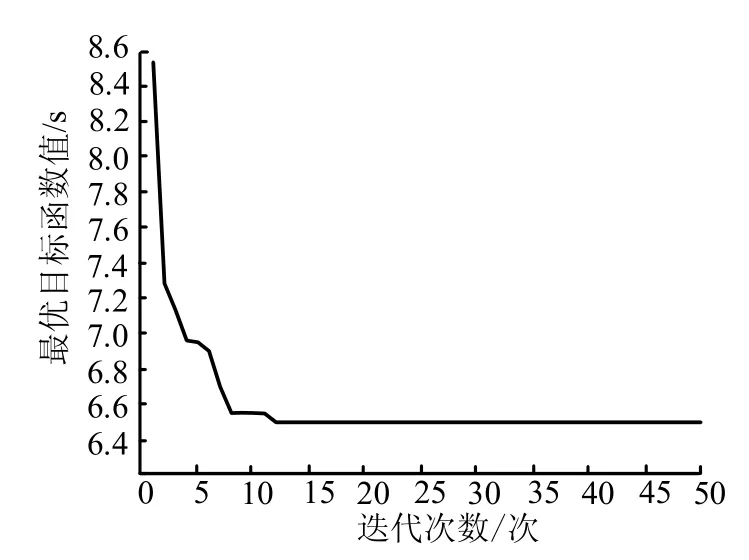
圖2 最優目標函數值f（x）變化曲線Fig.2 Curve of Optimal Objective Function Value

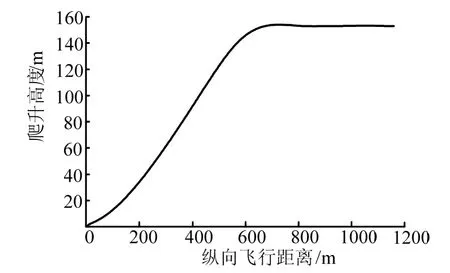
圖3 優化后的爬升段彈道曲線Fig.3 Curve of Ascent Trajectory

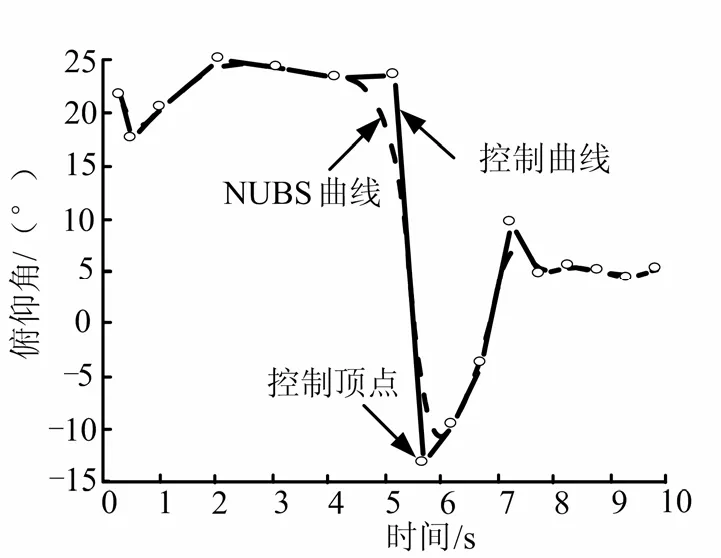
圖4 控制頂點、控制曲線以及NUBS曲線Fig.4 Control Points of NUBS and NUBS Curve

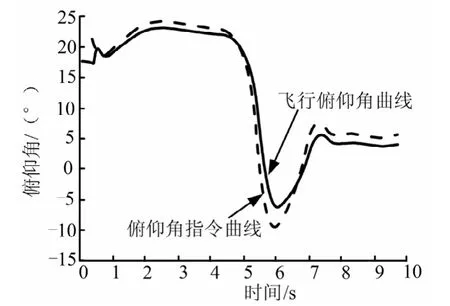
圖5 俯仰角及控制指令曲線Fig.5 Curves of Pitch Angle and Control Law

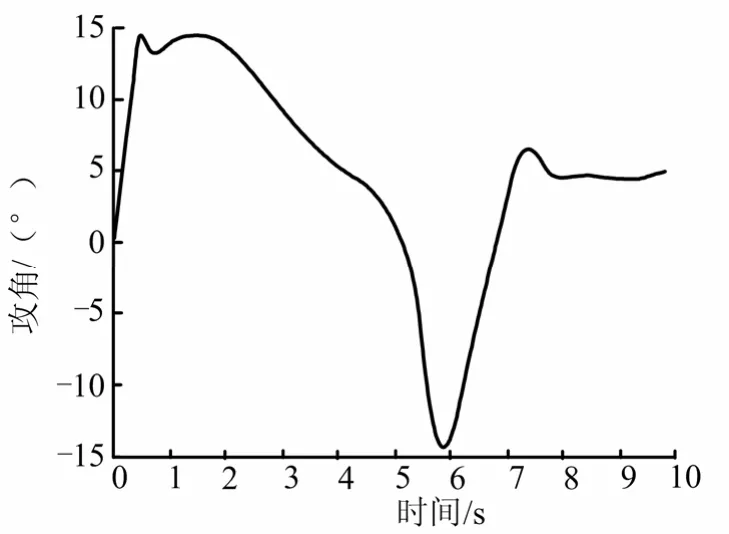
圖6 攻角曲線Fig.6 Curve of Attack Angle

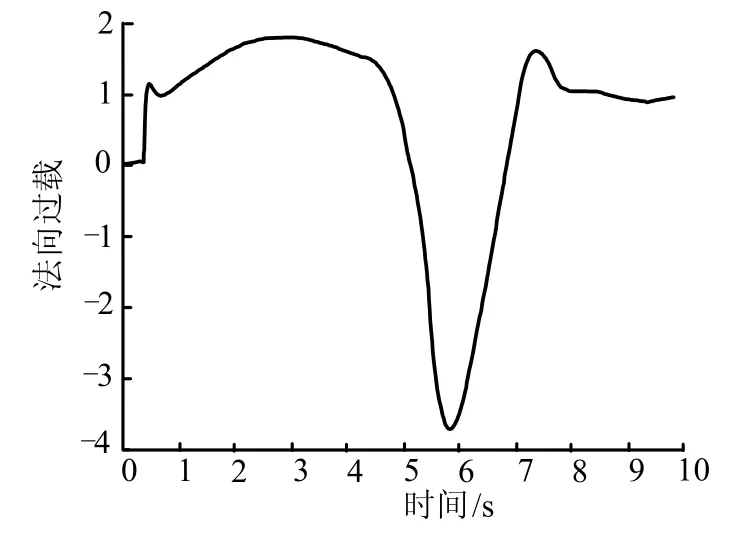
圖7 法向過載曲線Fig.7 Curve of Normal Overload

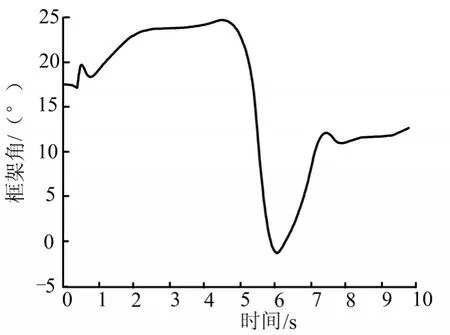
圖8 框架角曲線Fig.8 Curve of Gimbal Angle

如圖2所示，結合了非一致性變異及自適應變異的免疫克隆算法收斂速度較快，迭代開始后可迅速逼近最優值，且在第12次迭代就已經非常接近最優值。圖3為優化后的爬升段彈道曲線，根據優化后的控制指令，飛行器不僅可以在6.5 s內爬升到指定高度，而且滿足了導引頭框架角的約束條件，在不丟失目標的情況下順利地轉入平飛。

圖4為由控制頂點生成的NUBS曲線，由控制頂點聯接成的多邊形可以近似看作NUBS曲線的外接多邊形。通過圖5中俯仰角以及控制指令的對比可以看出俯仰角較好地跟蹤了指令的變化，說明控制系統在設計指令下始終處于平穩可控的工作狀態。

如圖6及圖7所示，在爬升初始階段以及轉平初始階段，即在t=0.5～2 s以及t=5.7 s時，攻角非常接近臨界攻角，法向過載絕對值也較大，說明飛行器在爬升段充分發揮了臨界攻角所允許的機動性能。根據圖8所示，框架角在爬升段全程均處于可用范圍。

分析表明優化后的飛行方案較好地滿足了飛行器對爬升段飛行方案的需求。同時優化方案簡單清晰，具有較高的效率，對免疫克隆選擇算法在其他飛行器設計領域的應用也具有一定的參考價值。

5 結 論

爬升段彈道的設計是彈道設計中的重要課題。本文結合無人飛行器爬升段采用的按俯仰角規律飛行方案，應用NUBS對飛行方案進行了參數化描述，采用ICSA進行了彈道優化設計，并根據實際應用設計了基于ICSA的無人飛行器爬升飛行方案優化流程。仿真結果表明優化后的飛行方案較好地滿足了飛行器對爬升段彈道的需求。同時優化方案簡單清晰，具有較高的效率，對免疫克隆算法應用在飛行器設計領域的其他方面也具有一定的參考價值。