基于代理模型和線性近似的快速氣動熱邊界求解方法

王 洋，袁軍婭，王洪興

（1. 北京航空航天大學，北京，100191；2. 航空工業第一飛機設計研究院，西安，710089；3. 北京衛星環境工程研究所，北京，100029）

0 引 言

高超聲速飛行器一般是指飛行馬赫數大于 5的飛行器，飛行器與大氣劇烈摩擦，產生強烈的氣動加熱。同時與結構之間發生復雜的耦合作用。在流固耦合分析中，表面熱流是流固邊界傳遞的關鍵參數。高超聲速氣動熱與來流條件（飛行高度、馬赫數、攻角等）、表面溫度和結構形狀密切相關。目前，在高超聲速流固耦合研究中，氣動加熱的計算方法主要分為工程計算和計算流體力學（Computational Fluid Dynamics，CFD）數值計算。工程算法基于邊界層理論或者實驗經驗關系式，主要用于求解簡單外形飛行器的氣動熱問題，對于復雜外形，由于其流場復雜，存在流動分離、激波-附面層干擾等現象，單純的工程方法難以滿足要求[1,2]。隨著計算機和CFD數值計算方法的不斷發展，已經能夠針對復雜外形開展全尺寸三維流場仿真計算，但是效率仍舊較低，不能滿足快速工程研制的需求。CFD降階模型的研究成為解決這類高超聲速氣動熱問題的一種有效途徑，可以克服工程方法不夠精確和CFD計算耗時的問題。

本文從兩個方面著手，減少流固耦合分析中熱邊界的計算耗時。一方面應用本征正交分解（Proper Orthogonal Decomposition，POD）降階代理模型，建立一種快速計算高超聲速氣動熱的方法。另一方面引入基于換熱系數的線性近似方法進行熱邊界傳遞，通過減少因壁溫引起的流場計算迭代次數來縮短流固耦合計算時間。以三維翼面為例，驗證了該方法有效性。

1 本征正交分解與代理模型

降階就是利用一個簡單的模型來代替CFD的來流條件和計算結果之間復雜的非線性關系，其中POD方法已經被很多研究人員采納，并得到一定的成果。Burkardt等人[3]用該方法得到了N-S方程的降階模型；Carlson和Roveda[4]將弱化形式的動量守恒方程投影到由速度相關的POD基函數形成的降階空間，建立了一組低維的POD系數為狀態變量的微分方程組來預測和控制翼面上的氣動力，對 CFD和降階模型（Reduced Order Model，ROM）的數據結果進行對比研究指出ROM利用少量的POD基模態能夠準確地反映系統的動態特征。除此之外，POD方法還被應用在最優控制[5～7]、流體力學[8～10]、熱傳導[11,12]分析中，極大地縮短了計算時間，提高計算效率。

POD方法是一種將復雜系統分解為數個基本模態的方法，在基本模態中包含著原始系統的主要特征，利用少量的基本模態就可以表達復雜的原始系統的特征，得到原始系統的ROM。利用實驗或者CFD數值計算得到一系列不同輸入條件下的響應輸出采用列向量的形式構成向量組，通過矩陣運算得到一組規范正交基，使得數據集合在這組基上的投影最大。通過對矩陣進行奇異值分解就可以得到正交基Φ以及特征值，由于矩陣S并非方陣，所以得到的特征值應該是方陣的特征值。特征值的大小表征了該特征值對應的特征向量，即POD基所包含的響應輸出集合的特征的多少。通常通過廣義“能”E來表征[13]前n個POD基所包含原系統特征的權重，廣義能定義為

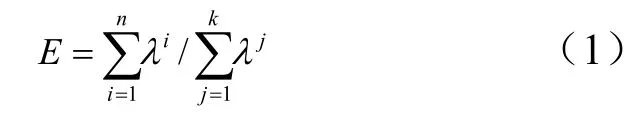
式中 λ為特征值；n為POD基的個數；k為系統樣本點個數。

通常特征值從大到小衰減很快，這樣廣義能 E會趨近于1，前面幾個POD基就能包含絕大部分的集合特征。通過對特征向量的個數進行截斷，取前面部分基來表達整個系統，從而將全階系統投影到低維空間。

代理模型的基本思想是通過數學方法，利用已有的輸入和輸出參數，構造出一個和原始計算結果相近的數學模型[14]。目前常用代理模型有多項式響應面模型、Kriging模型和徑向基函數等，本文采用 Kriging模型。

式中 f(X)為回歸模型，代表確定的函數； z(X)為一個均值為0，方差為σ2的隨機過程，其協方差為

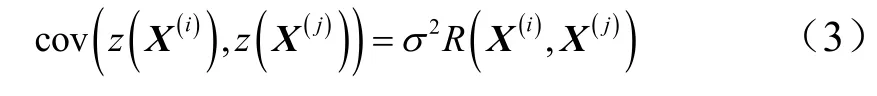
式中 R為兩個輸出參量 X(i)和 X(j)的相關函數，與兩點在空間的位置相關，關系式為

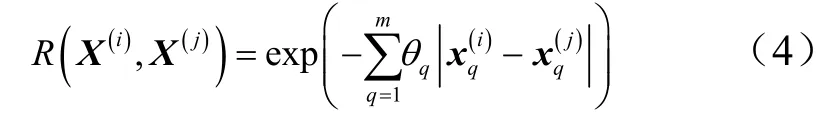
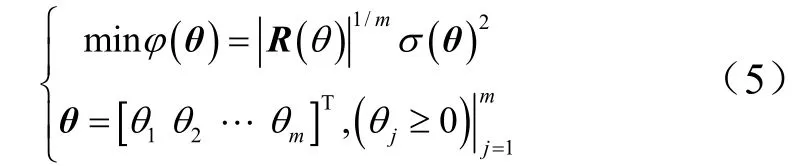
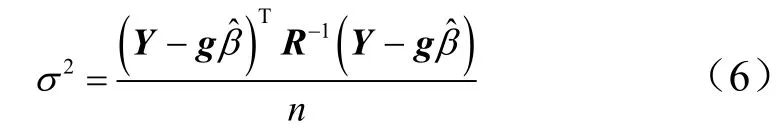
其中，

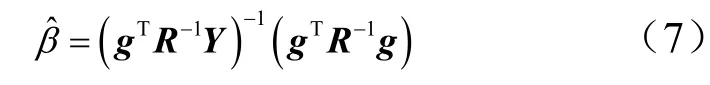
式中 g為所有元素為1的向量。這樣Kriging模型可以表示為

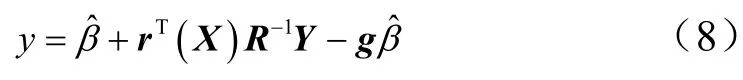
給定一個新的輸入參數向量X，即可通過該模型預測輸出參數。因此只需要將帶約束的優化問題解決，得到θ，就可以構建出此模型來。一般通過遺傳算法來求解最優的θ向量。

POD方法通過利用全階模型計算結果建立一組最佳充分描述全階系統動力學特性的正交基來描述系統的主要特性[16]。代理模型的目的是得到原系統樣本點與截斷后POD基投影系數的一一對應關系。本文以高超聲速飛行器機翼氣動熱計算為例，建立POD-Kriging代理模型，過程包括：

a）選取馬赫數、飛行高度和飛行攻角為設計變量，根據飛行軌道設計變量變化范圍，確定設計變量空間，采用拉丁超立方試驗設計方法在給定的變量范圍內獲得設計空間樣本I=[Ma,α,H]。

b）采用數值計算方法得到各樣本點對應響應輸出，以表面熱流為例，輸出即為飛行器表面所有網格點給定壁溫條件下的熱流q，構建系統的特征矩陣

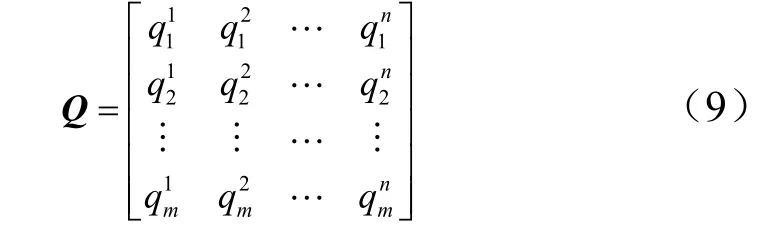
式中 n為樣本點個數；m為網格點個數。

c）將系統矩陣Q進行奇異值分解，利用公式[15]：

對于給定樣本空間范圍內的任意計算狀態，利用這個近似擬合關系得到POD基系數，從而得到q的近似響應值。

2 模型以及算例分析

2.1 模型和設計空間的選取

本文以戰斗機 F-104機翼模型為例，分析基于POD-Kriging代理模型獲得高超聲速氣動熱的過程、精度和計算效率。該模型常被用來做高超聲速分析，機翼相關參數如圖1所示。

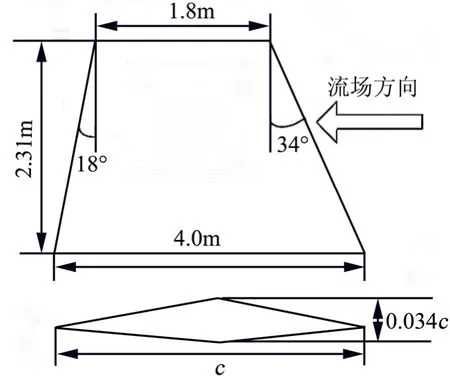
圖1 機翼外形Fig.1 Shape of the Wing c—弦長

機翼外流場模型采用ICEM網格繪制軟件劃分，分為8個block，對機翼附近網格進行附面層加密，網格如圖2所示，網格數為197.6萬。

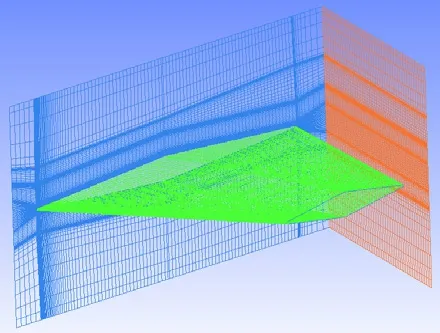
圖2 機翼外流場網格Fig.2 Wing Outflow Field Grid

機翼的氣動熱設計變量和設計空間如表1所示。

表1 機翼氣動熱設計變量和設計空間Tab.1 Aerodynamic Heat Design Variables and Space of Wing

2.2 POD-Kriging代理模型的建立

在給定的設計空間內，經過拉丁超立方抽樣，得到的100個樣本點的初始來流條件，如表2所示。

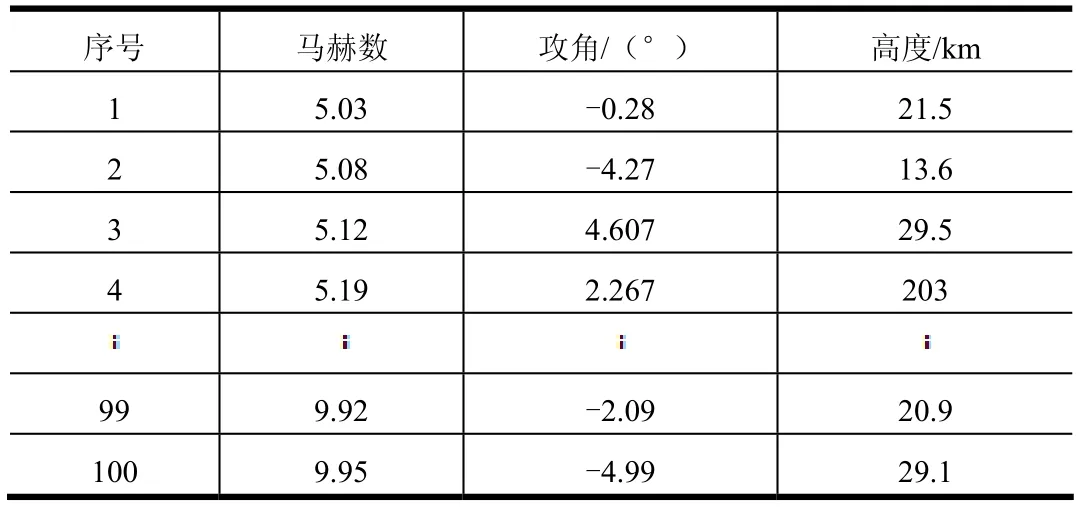
表2 樣本點數據Tab.2 Sample Point Data

對于每一個樣本點，本文采用CFD-Fastran軟件計算翼面熱流分布。CFD-Fastran常用于高超聲速飛行器外流場計算，文獻[17]通過數值計算與試驗對比，得出結論CFD-FASTRAN軟件的k-ε及B-L兩種模型求解高超聲速氣動熱問題均能達到較好的準確度，且 B-L模型計算速度快、使用方便。本文采用 B-L湍流模型，空間采用高階AUSM格式，時間采用隱式迭代格式。以計算得到的不同來流條件下恒壁溫的熱流分布Q為基礎，建立POD-Kringing代理模型。

2.3 代理模型計算結果分析

以熱流Q為例，說明代理模型的計算精度。經過POD方法分解得到100個基模態的熱流分布，圖3為每一個基模態對應的特征值的對數曲線，特征值的大小表征了基模態對于熱流分布的貢獻，可以看出前10階包含了大部分熱流的特性。

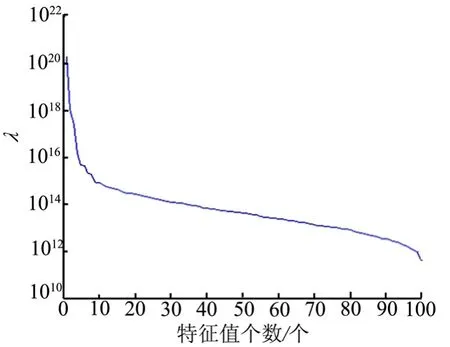
圖3 基模態對應的特征值Fig.3 Eigenvalues of the Corresponding base Mode

2.3.1 典型工況算例分析

在給定的樣本空間里隨機取某一個測試點，進行CFD計算，然后與POD-Kriging代理模型的預測結果進行比較，在每個網格點進行相對誤差計算，誤差計算公式為

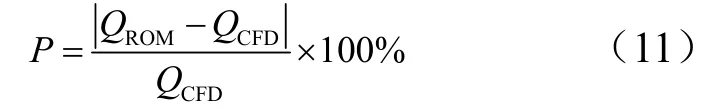
式中 ROM為用代理模型方法得到的熱流預測值；CFD為用CFD-Fastran計算得到的熱流值。

圖 4為在流條件為飛行高度 H=20 km，攻角α=0°，馬赫數Ma=7.5的情況下CFD計算的熱流值與 POD-Kriging模型預測的熱流值的相對誤差分布。由圖4可以看出，在機翼前緣處，二者的結果比較接近，在后緣部分，誤差有所增加，誤差最高的地方集中在前緣后部靠近翼根處，達到7%左右。結果表明，對于單個測試點，POD-Kriging代理模型的預測結果比較準確。

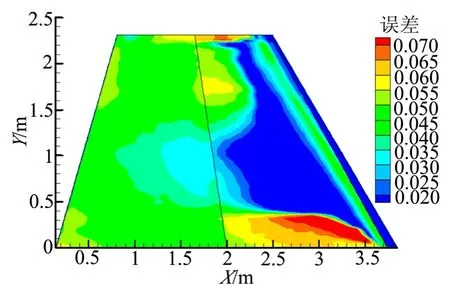
圖4 馬赫數為7.5來流翼面平均誤差分布Fig.4 Average Error Distribution of the Wing Surface with the Maher Number of 7.5

2.3.2 測試樣本點的相對平均誤差

在輸入參數的空間內隨機選取10個測試樣本點，測試樣本點的輸入參數如表 3所示。分別采用CFD-Fastran計算和代理模型計算熱流分布，利用式（11）計算每個測試樣本點的誤差值Pi，10個樣本點的相對平均誤差為

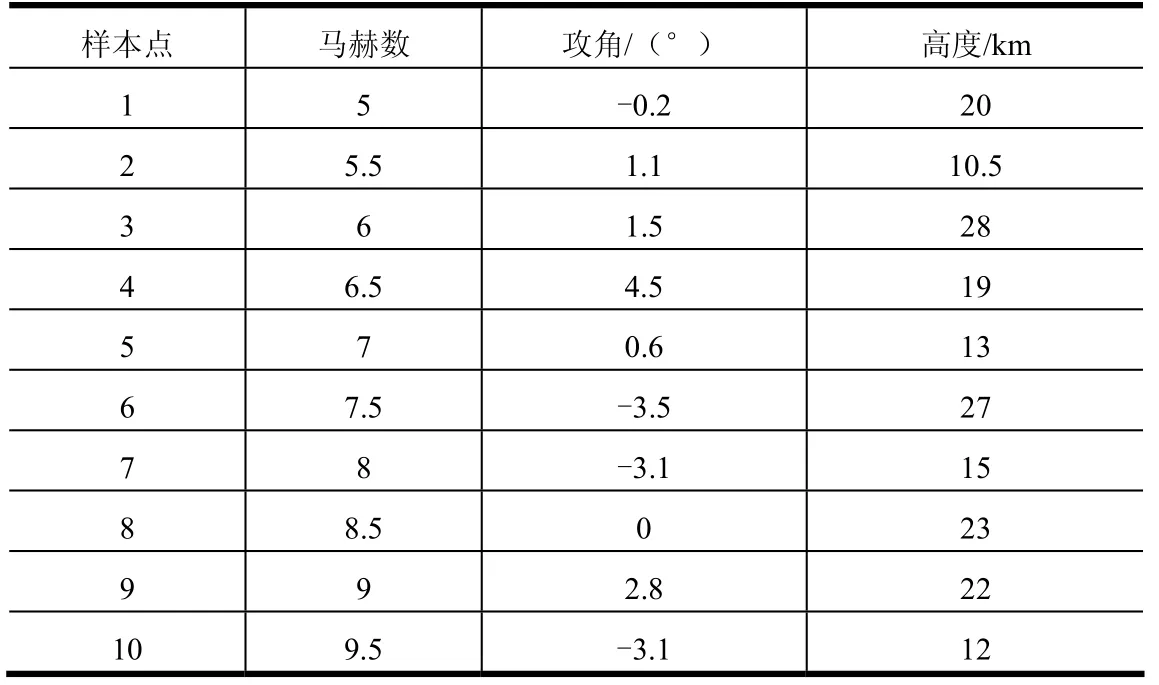
表3 隨機選取的10個樣本點輸入參數Tab.3 Input Parameters of Randomly Selected 10 Sample Points

用POD-Kriging方法得到的10個測試樣本點的翼面熱流平均相對誤差云圖，如圖5所示。

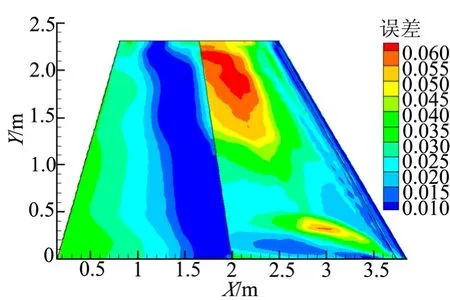
圖5 10個樣本點翼面熱流密度平均誤差分布Fig.5 Average Error Distribution of Heat Flow Density of Wing Surface at 10 Sample Points

從圖5中可以看出，翼面誤差基本小于6%，前緣處誤差較小，誤差較大的地方集中在上翼面凸起處和下翼面局部。

2.3.3 POD基模態個數影響

預測的準確程度與POD基模態的個數有關，圖6顯示的是基模態為15，20，25，30時，代理模型的熱流預測值和CFD計算值的相對誤差。

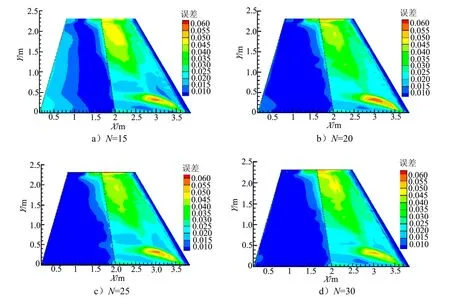
圖6 不同基模態個數下平均誤差分布的變化云圖Fig.6 Variation of Mean Error Distribution under Different Fundamental Mode Numbers

由圖 6可知，隨著基模態個數的提高，平均誤差逐漸變小，而且當基模態個數在20以后，平均誤差的變化較小，誤差最明顯的地方集中在翼面凸起處，且最高誤差在6%左右。

3 熱邊界線性化近似

3.1 熱邊界線性化近似方法

在一定樣本基礎上，通過建立 POD-Kriging代理模型，可以快速得到高超聲速飛行器不同飛行條件下給定壁面溫度的表面熱流分布。而在一般的高超聲速飛行器流固耦合研究中，通常會采用松耦合的方式，即將流場、固體結構場和溫度場分開計算。以假定表面溫度得到熱流，再進行結構計算，不斷迭代到誤差在要求范圍內。每一次CFD計算都要耗費大量的計算時間，給耦合仿真的工程應用帶來困難。引入線性化近似的方法[18]可以改善CFD迭代耗時問題，即：傳遞熱邊界時，采用線性近似來計算新壁溫條件下高超聲速飛行器表面氣動熱，以代替CFD迭代計算熱流，必要時再采用CFD或者代理模型迭代計算，某些情況下，這種近似在不進行CFD迭代的情況下也可以獲得滿足工程需要的計算結果。

熱流計算表達式為

式中 h為換熱系數；wT為壁面溫度；awT為絕熱壁面溫度。

如果壁面溫度對換熱系數的影響較小，就可以以飛行器的換熱系數和絕熱壁溫作為對象，建立POD-Kriging模型，那么熱流就是壁面溫度的線性函數。在耦合計算過程中，當表面溫度變化時，可以通過換熱系數和絕熱表面溫度直接得到變化后的表面熱流，而不需要通過新的CFD計算得到表面熱流。

建立絕熱壁溫的 POD-Kriging模型過程與建立熱流的 POD-Kriging模型過程相同，只是樣本點計算的響應輸出是絕熱壁溫。建立換熱系數的 POD-Kriging模型，需要同時計算定壁溫表面熱流和絕熱溫度來獲得。

假設壁面溫度與來流溫度T∞相同時，表面熱流為

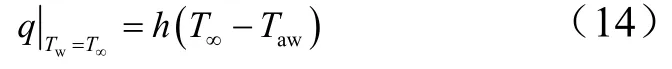
忽略壁面溫度對換熱系數的影響，則換熱系數可以通過下式計算：

對于每個樣本點，需要計算壁溫為來流溫度的熱流分布和絕熱壁溫分布，以此數據為基礎，建立換熱系數和絕熱壁溫的POD-Kriging模型。

3.2 換熱系數誤差分析

取來流條件為飛行高度 H=29.9 km，攻角α=0.9°，馬赫數 Ma=9.08，采用CFD分別計算此條件下絕熱壁面的溫度分布awT和給定溫度為300 K條件下的熱流分布由式（15）求出換熱系數1h。改變壁溫為500 K，求出此時的熱流同樣求出換熱系數對比熱流和換熱系數的變化。

圖7為改變壁溫前后，各網格點的熱流變化。

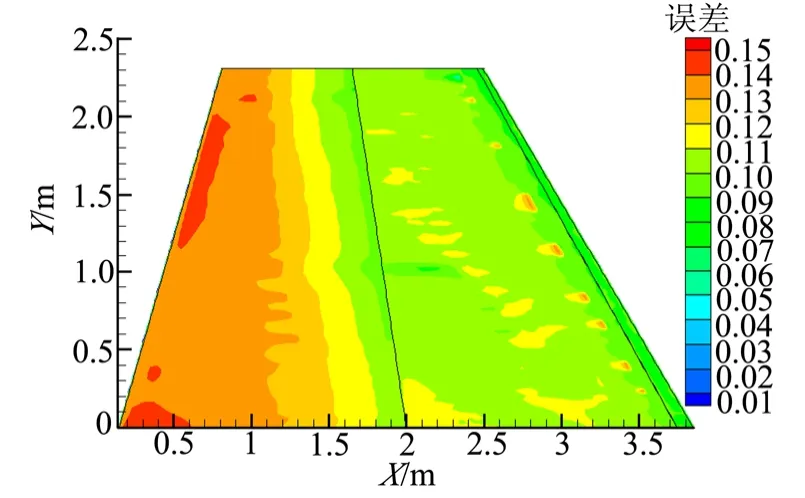
圖7 改變壁溫引起的熱流的變化Fig.7 Change of Heat Flux Caused by Wall Temperature

圖8為換熱系數在溫度改變前后的變化。

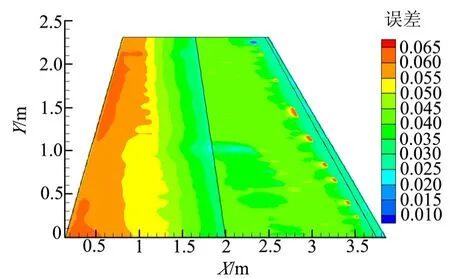
圖8 改變壁溫引起換熱系數的變化Fig.8 Change of Heat Transfer Coefficient Caused by Changing Wall Temperature

由圖7、圖8可以看出，與對熱流的影響相比，溫度變化對于換熱系數的影響較小，變化率在6.5%以內。

溫度改變后，由式（13）利用線性化方法求解新的熱流，與CFD得到的熱流進行比較，圖9為二者計算熱流結果的相對變化。

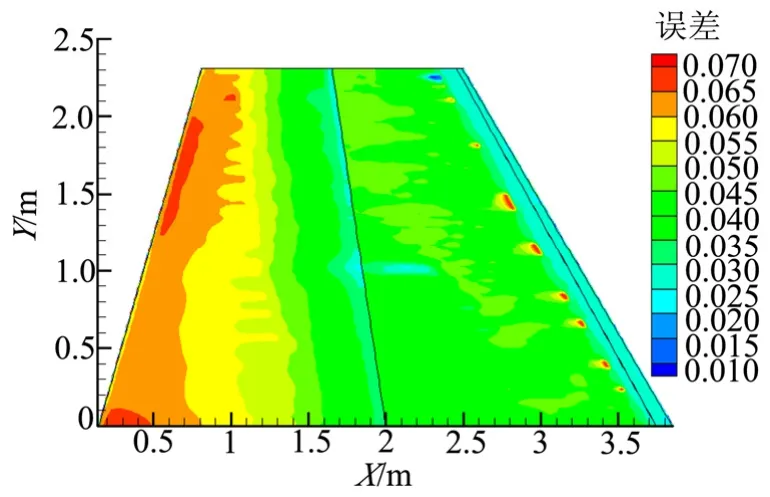
圖9 線性化處理和CFD結果的相對變化Fig.9 Relative Change of Linearization and CFD Results

由圖9可以看出，線性化處理得到的壁溫變化后熱流與CFD計算結果相對誤差基本在7%以下。在計算過程中，CFD計算一次需要10 h以上，而采用線性化處理只需不到1 s，極大提高了計算效率。

3.3 代理模型結合線性化近似結果分析

取飛行高度 H=29.9 km，攻角α=0.9°，馬赫數Ma=9.08作為來流條件，利用POD-Kriging代理模型快速計算該狀態下冷壁熱流和絕熱壁的溫度，再利用式（13）可以求出壁溫改變為500 K后的表面熱流，同時采用CFD-Fastran計算壁溫改變為500 K后該狀態的表面熱流，圖10顯示的是二者的相對誤差。從圖10中可以看出，前緣誤差較小，在2.5%以內，后緣誤差較大，整個翼面的誤差值在7%以內。和圖9相比，誤差較大的網格點有所增多，這是因為絕熱壁溫是經過POD代理模型的預測值，增加了誤差。

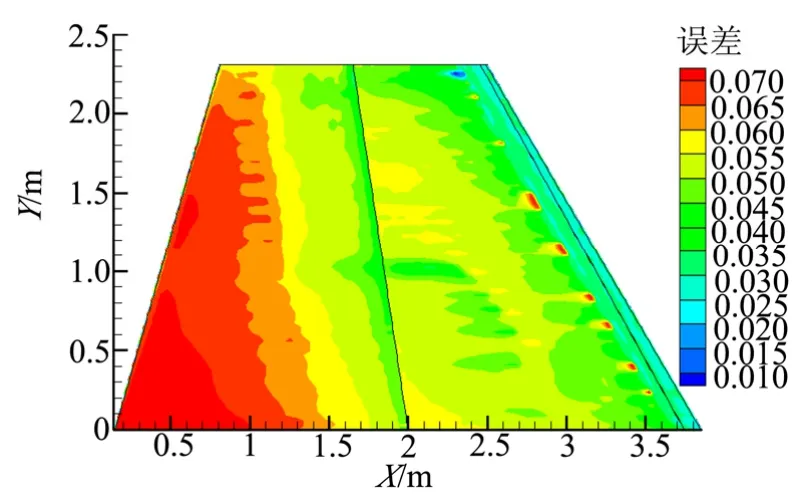
圖10 POD-Kriging模型和CFD結果的相對誤差Fig.10 Relative Error of the POD-Kriging Model and the CFD Result

4 結 論

本文以減少流固耦合過程中熱邊界的求解時間為目標，一方面基于 POD-Kriging代理模型建立快速計算不同狀態的氣動熱參數分布的方法；另一方面提出基于換熱系數的線性近似方法確定熱邊界，以三維機翼為例，分析了方法的可行性，得到以下結論：

a）對高超聲速飛行器機翼氣動熱提出的POD-Kriging代理模型結合的方法，成功實現模型的降階，代理模型的熱流計算誤差在7%之內；

b）在POD-Kriging建模過程中選取的基模態個數對代理模型預測結果會產生影響，結果表明增加基模態個數在一定程度上能夠提高預測精度，當其達到20后，預測誤差變化很微小；

c）引入換熱系數線性近似的方法，能夠節省耦合計算過程中因壁溫變化引起的流場迭代步驟，在不降低熱流計算精度的前提下，可以縮短計算時間。

本文建立的方法在滿足一定計算精度的條件下，極大地提高計算效率，促進高超聲速飛行器再入過程中的流固耦合分析或多物理場優化設計的工程應用。