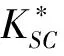基于模型約束逆建模的儲層物性參數估計方法

劉 倩， 董 寧， 季玉新， 陳天勝

(中國石油化工股份有限公司 石油勘探開發研究院，北京 100083)

0 前言

儲層物性參數是了解油氣儲層的物理特性和幾何特性的必備要素，因此將儲層彈性參數轉換為儲層物性參數的方法一直是儲層地球物理的研究熱點之一。最簡單、也是早期儲層物性參數估計中常用的策略是基于統計學理論建立彈性參數(速度、密度、阻抗等)和物性參數之間的經驗關系實現物性參數的間接估計[1-4]。

對于復雜的儲層而言，簡單的統計擬合得到的經驗關系不足以準確描述彈性參數和物性參數之間的復雜關系。巖石物理模型作為連接儲層的彈性性質與物理性質的紐帶，被越來越多地應用于儲層物性特征的描述中。針對不同巖石的礦物組成、孔隙類型等物理性質，學者們建立了不同的巖石物理模型。Voigt - Reuss - Hill模型和Hashin-Shtrikman-Walton模型建立了礦物的彈性性質與巖石基質的彈性性質之間的關系[5-6]；接觸模型(CT模型)和接觸膠結模型(CCT模型)可以用于計算高孔隙或弱膠結的巖石的彈性性質[7-9]；Kuster-Toks?z模型、微分等效介質模型(DEM模型)和自相容近似模型(SC模型)可以用于膠結程度較強的巖石的彈性性質的研究[10-13]。

巖石物理建模理論的發展推動了儲層物性參數估計技術的發展。Mukerji等[14]和Eidsvik等[15]基于信息論提出了統計巖石物理方法來反演儲層物性參數；Bachrach等[16]綜合運用巖石物理隨機建模方法和貝葉斯反演理論來反演孔隙度和含水飽和度；Yin等[17]建立了基于FFT-MA模擬方法和GDM擾動方法的地質統計學物性參數反演方法；Alvarez等[18]基于巖石物理理論提出了多屬性旋轉技術來估計儲層物性參數；Gui等[19]基于貝葉斯反演框架建立了彈性參數加權統計的儲層物性參數反演方法；李志勇等[20]利用疊前地震同步反演來實現儲層物性參數和彈性參數的同步預測；Boateng等[21]基于Caianiello神經網絡算法和Levenberg-Marquardt最優化算法提出了高精度的孔隙度反演方法。

筆者以巖石物理理論為基礎，在三維儲層參數域進行巖石物理建模，選取三種彈性參數作為輸入數據，計算出彈性參數在儲層參數域的等值面，利用三個等值面的空間交會，在模型約束條件下同時估計出孔隙度、泥質含量和含水飽和度三種儲層物性參數。通過模型實驗和實際工區應用實例，檢驗了方法的有效性和實用性。

1 方法原理

巖石物理模型建立了儲層物性參數和彈性參數的聯系，這種聯系是儲層物性參數估計的基礎，因此根據目標儲層的性質建立合理、準確的巖石物理模型是準確估計物性參數的前提[23]。

建立巖石物理模型[24]，建模過程中的基本參數如表1所示。

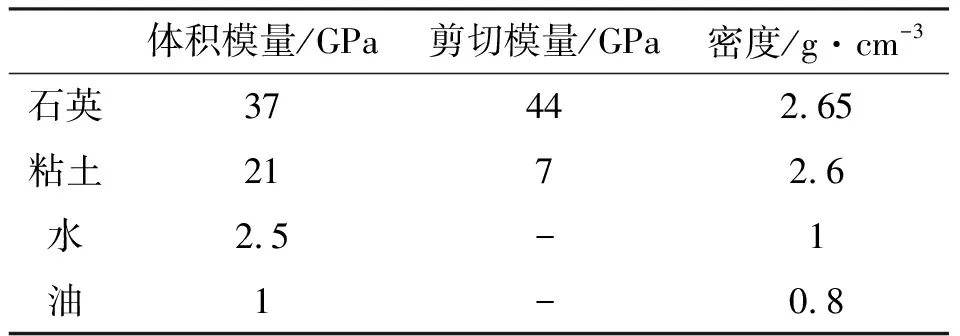
表1 基本組分參數表

儲層特征描述最常用的參數是孔隙度φ、含水飽和度Sw和泥質含量Vsh，建立一個三維直角坐標系，分別以Vsh、φ、Sw作為x、y和z軸，坐標軸的范圍分別是0～1、0～0.4和0～1，各坐標軸均勻采樣，該坐標系稱為一個儲層參數域。在這個儲層參數域中，每個點的坐標就是一組儲層物性參數，根據巖石物理模型正演方法計算彈性參數值，并在整個參數域內對彈性參數進行插值就建立了彈性參數的三維數據體d。

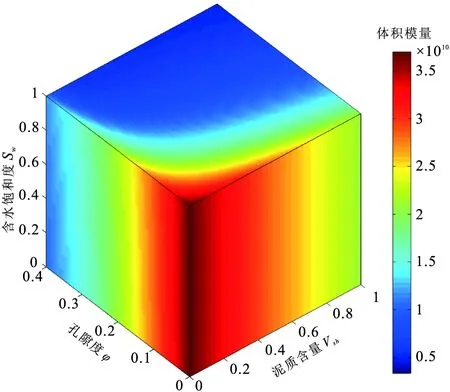
圖1 儲層參數域的彈性參數數據體圖Fig.1 Elastic parameter data cube in reservoir parameter domain

圖1是體積模量的三維數據體，根據相同的原理可以建立剪切模量和密度的三維數據體。已知地下儲層中某點的實測彈性參數數據d0(K0,μ0,ρ0,λ0,σ0)，要同時進行三種物性參數的估計需要至少有三種彈性參數，可以根據儲層特點靈活選取彈性參數種類(如體積模量K0、剪切模量μ0和密度ρ0)。

采用Marching Cubes算法分別在體積模量、剪切模量和密度的數據體中計算出值為K0、μ0和ρ0的等值面[23]。在等值面的拓撲結構比較簡單的情況下，經典的Marching Cubes算法就可以完成；在等值面的空間構型較為復雜情況下，需要使用改進的Marching Cubes算法[25]，以保證曲面擬合的精度和效率。

如圖2(a)是值為K0的體積模量的等值面圖，該等值面可以用SK0(Vsh,φ,Sw)表示。同理可以得到密度在儲層參數域的等值面Sρ0(Vsh,φ,Sw)，將等值面SK0(Vsh,φ,Sw)和等值面Sρ0(Vsh,φ,Sw)交會在同一個儲層參數域中，即可找到同時滿足體積模量為K0和密度值為ρ0的點，如圖2(b)所示，這些點就分布在兩個等值面的交線lK0 ρ0上。

為了得到交線上各點的坐標，建立如方程(1)的目標函數，在兩個等值面的定義域交集內求取目標函數的最小值。

J1=‖SK0-Sρ0‖2

(1)

其中：SK0、Sρ0是等值面SK0(Vsh,φ,Sw)和Sρ0(Vsh,φ,Sw)內的所有點。

作為輸入數據的彈性參數通常是地震反演的結果或者測井數據重構的結果，因此其中通常包含一定的誤差。為了提高算法的穩定性、減少輸入數據的誤差對估計結果精度的影響，在方程(1)加入模型約束項，目標函數變為式(2)。

‖Sρ0-m‖2

(2)

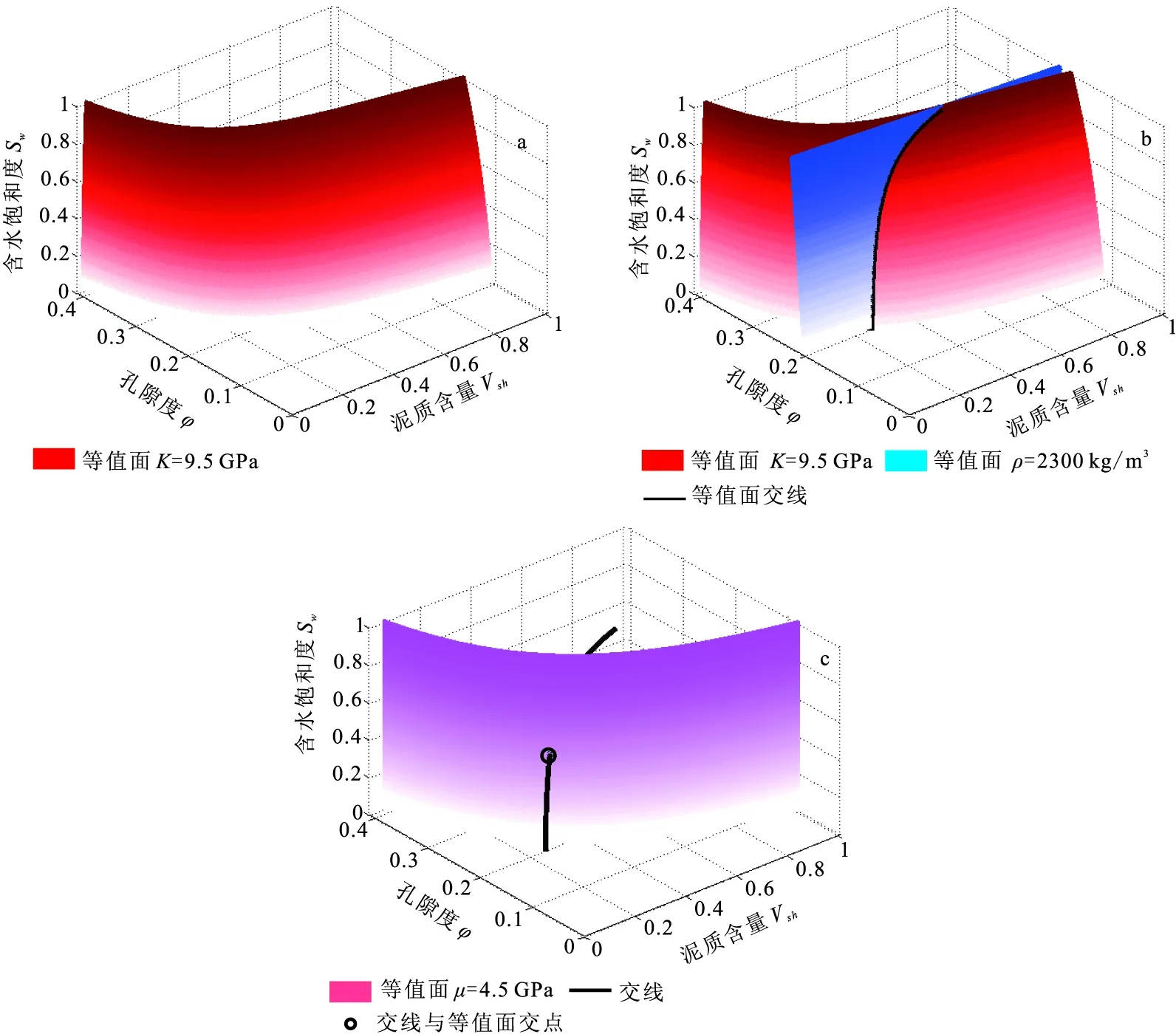
圖2 儲層參數域的等值面圖及其交會圖Fig.2 Isosurfaces and intersection of isosurfaces in reservoir parameter domain(a)體積模量等值面圖；(b)兩個等值面的交會圖；(c)交線與剪切模量等值面的交會圖

其中，在井位置處m是實際測井測得的儲層物性參數，作為模型約束；在井旁道的位置沒有測井數據，可以利用井間插值、地質統計學建模等方法建立的模型作為m進行約束。

計算出剪切模量為μ0在儲層參數域的等值面Sμ0(Vsh,φ,Sw)，將其與圖2(b)中的兩個等值面的交線交會在一起，結果如圖2(c)所示。圖2(c)中交線與等值面的交集部分是圖中黑色圓圈標出的點，這個點的體積模量為K0、剪切模量為μ0和密度為ρ0，則這個點的坐標就對應要估計的儲層物性參數。

建立如方程(3)的目標函數，同樣加入模型約束項。利用最優化算法在交線lK0 ρ0與等值面Sρ0的定義域交集內求取目標函數的最小值即可得到交點的坐標(0.20,0.30,0.49)。

J3= ‖LK0 ρ0-Sμ0‖2+ ‖LK0 ρ0-m‖2+

‖Sμ0-m‖2

(3)

其中:Sμ0是等值面Sμ0(Vsh,φ,Sw)內的所有點；LK0 ρ0是等值面SK0(Vsh,φ,Sw)和Sρ0(Vsh,φ,Sw)的交線上的所有點。

2 模型試算

2.1 抗噪性分析

為了檢驗本文提出的儲層物性參數估計方法的有效性，建立一個包含27個點的儲層物性參數模型，其孔隙度、泥質含量和含水飽和度數據如圖3所示。將這些模型數據與表1中的基本參數結合，利用參考文獻[20]中的巖石物理建模方法計算出一系列彈性參數：體積模量K、泊松比σ、密度ρ、拉梅參數λ和μ、縱波阻抗IP、橫波阻抗IS、楊氏模量E等。這里選取體積模量K、泊松比σ和密度ρ作為輸入數據進行儲層物性參數估計，結果如圖4所示。圖4中的黑色圓圈是模型數據，綠色實心點是估計結果，通過對比可知，估計結果與模型數據基本一致。

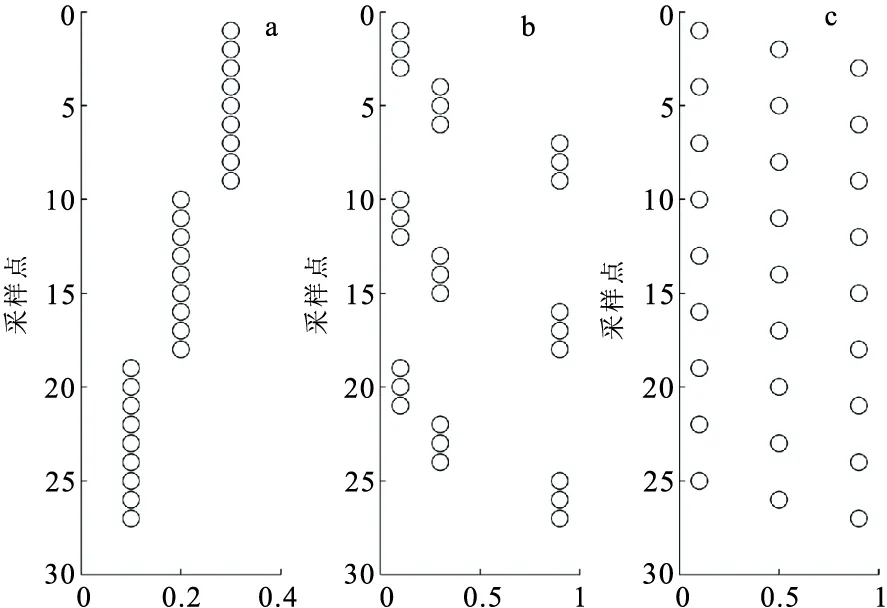
圖3 原始模型Fig.3 Original model(a)孔隙度;(b)泥質含量;(c)含水飽和度

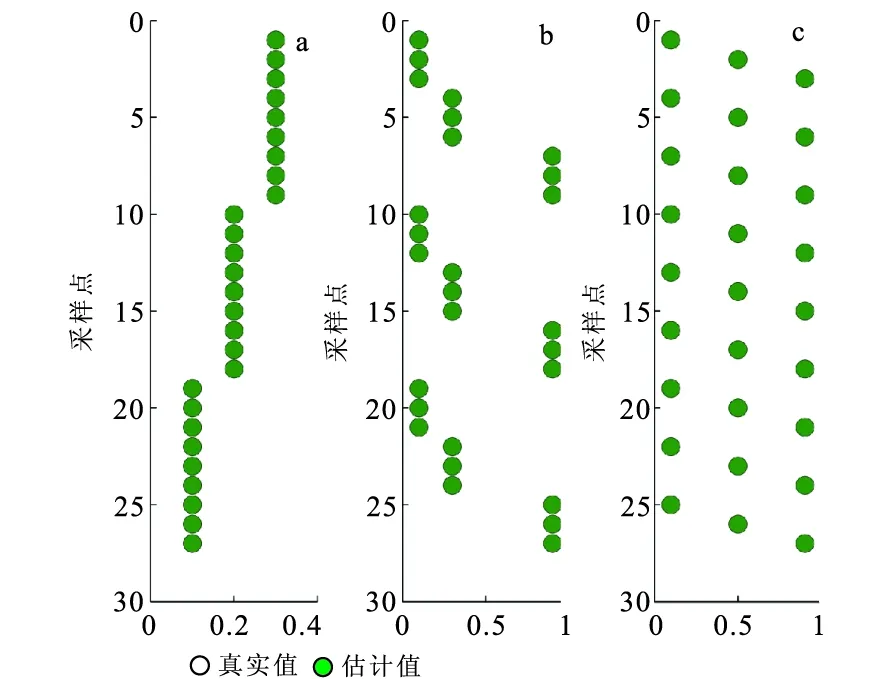
圖4 估計結果與原始模型的對比Fig.4 Comparison of estimations and original data(a)孔隙度；(b)泥質含量；(c)含水飽和度

實際數據(測井數據、地震數據、反演結果)都包含一定的噪音或者誤差。因此實際應用中，物性參數的估計過程會受到輸入數據誤差的影響。為了檢驗該方法的穩定性，在輸入數據體積模量K、泊松比σ和密度ρ中均加入8%的擾動，用于模擬包含誤差的輸入數據，然后分別進行無約束和有約束的估計。由圖5～圖7可以看出，有約束情況下的估計誤差遠小于無約束情況的估計誤差，證明了加入約束的必要性和有效性。

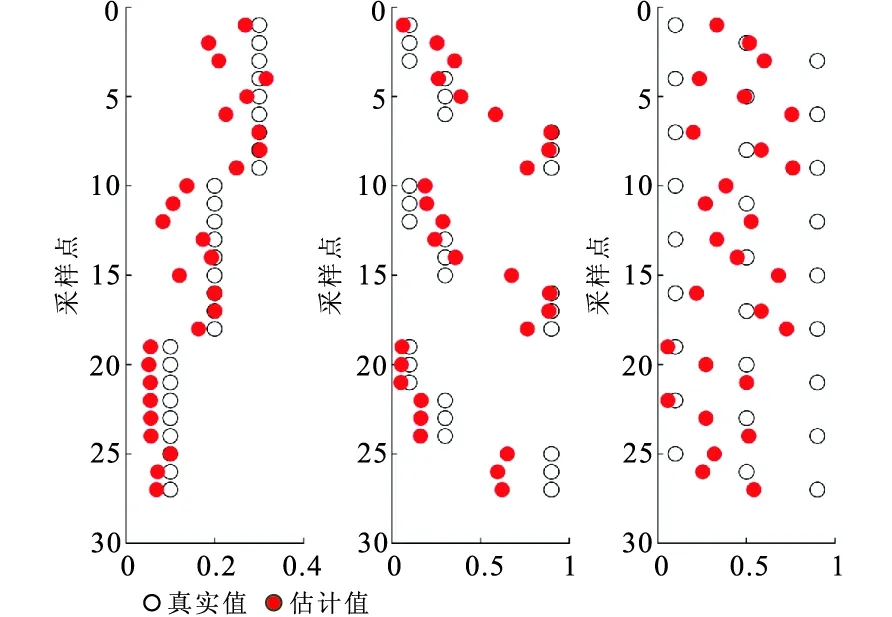
圖5 加入擾動后的無約束估計結果 與原始模型的對比Fig.5 Comparison of unconstrained estimations with perturbation and original data(a)孔隙度；(b)泥質含量；(c)含水飽和度

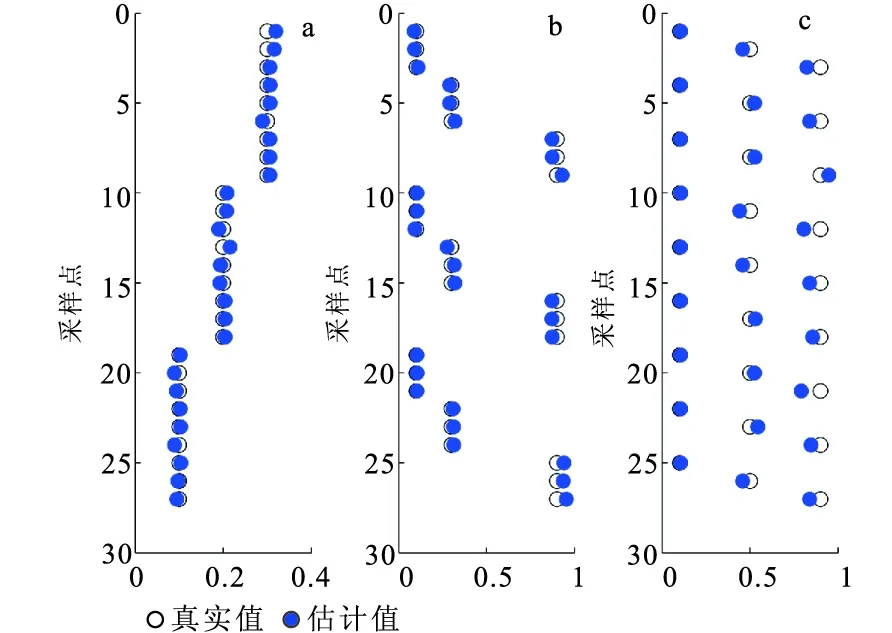
圖6 加入擾動后的有約束估計結果 與原始模型的對比Fig.6 Comparison of constrained estimations with perturbation and original data(a)孔隙度；(b)泥質含量；(c)含水飽和度

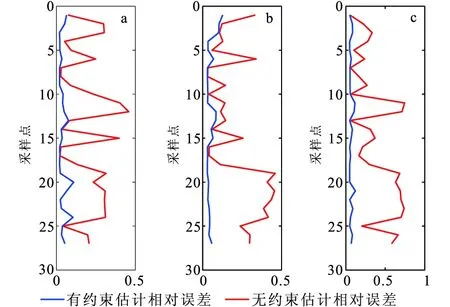
圖7 有擾動情況下有、無約束估計結果 的相對誤差絕對值對比Fig.7 Relative error comparison of constrained and unconstrained estimations with perturbation(a)孔隙度；(b)泥質含量；(c)含水飽和度

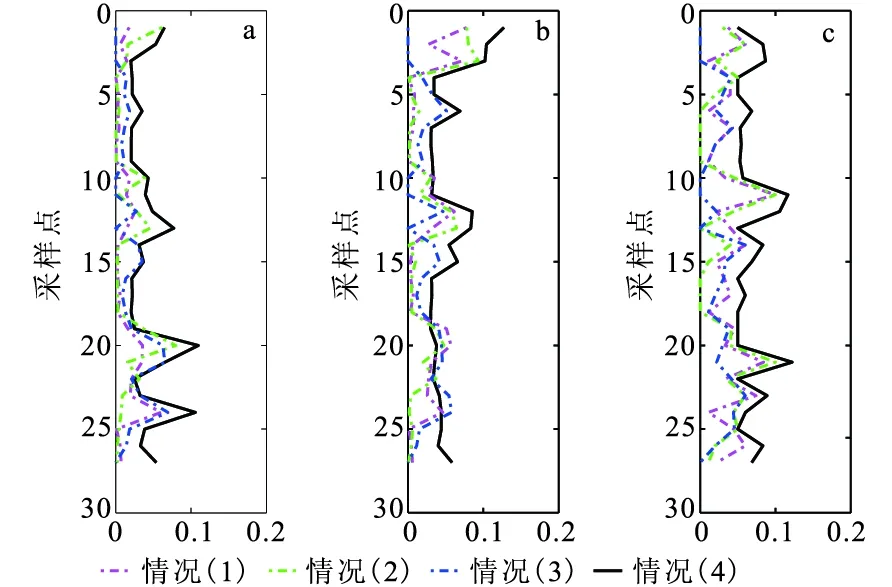
圖8 不同的輸入數據擾動引起的估計結果 的相對誤差絕對值對比Fig.8 Comparison of relative estimations errors from input data with different perturbations(a)孔隙度；(b)泥質含量；(c)含水飽和度

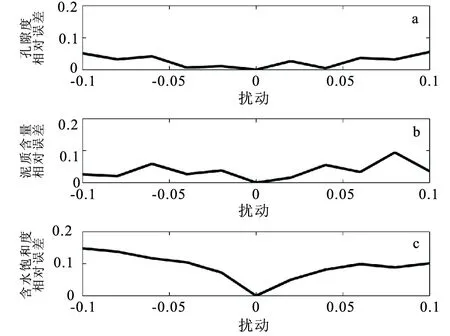
圖9 不同擾動情況下的估計結果的相對誤差絕對值Fig.9 Comparison of relative estimations errors from input data with different perturbations(a)孔隙度；(b)泥質含量；(c)含水飽和度

為了進一步檢驗本文方法的穩定性，在輸入數據中加入不同程度的擾動，加入的擾動包含如下三種情況：①體積模量8%，泊松比0%，密度0%；②體積模量0%，泊松比8%，密度0%；③體積模量0%，泊松比0%，密度8%；④體積模量8%，泊松比8%，密度8%。在這四種情況下分別進行物性參數估計，得到的結果如圖8所示。由圖8可以看出，前三種情況得到的估計結果精度接近，第四種情況誤差最大，而孔隙度和泥質含量的估計結果中第①種情況的結果略好。綜合四種情況而言，孔隙度和泥質含量的誤差小于含水飽和度的誤差。

在輸入數據體積模量、泊松比和密度中加入相等的擾動，擾動范圍是-8%到8%。利用有擾動的輸入數據進行有約束估計，然后將27個點的估計結果按照輸入數據擾動大小分別取平均值。圖9是估計結果的相對誤差的絕對值隨著擾動變化的變化圖。從圖9中可以看出，孔隙度受擾動影響最小，含水飽和度受擾動影響最大，且擾動絕對值越大，三種儲層物性參數的估計結果的誤差越大。

2.2 巖石物理模型的影響

為了研究不同的巖石物理模型對于儲層物性參數估計結果的影響，分別用微分等效介質模型(DEM模型，見附錄)和自相容近似模型(SC模型，見附錄)進行實驗。

利用Xu-White模型、DEM模型和SC模型計算圖4中的數據得到體積模量、泊松比和密度作為輸入數據。在輸入數據中各加入8%的擾動，分別進行儲層物性參數估計，結果如圖10所示。通過對比圖10可以看出，基于三種模型估計得到的儲層物性參數精度基本一致，證明模型的不同不會給估計結果帶來較大的影響。因此本文方法可以適用于多種不同巖性、不同巖石物理特點的儲層，只需在應用過程中根據儲層特征建立合理的巖石物理模型，獲取準確的模型參數。

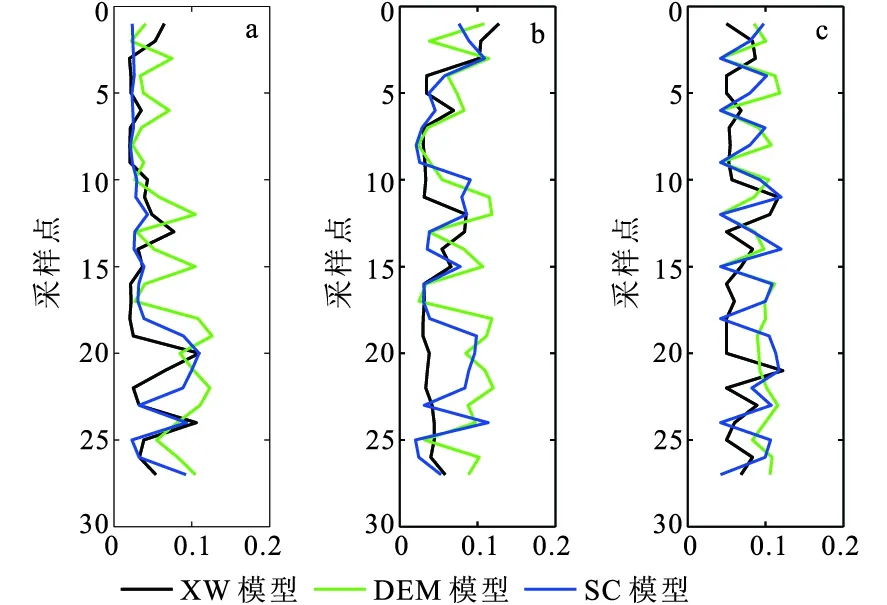
圖10 不同模型的估計結果相對誤差比較Fig.10 Comparison of relative estimation errors with different models(a)孔隙度；(b)泥質含量；(c)含水飽和度

3 實際應用

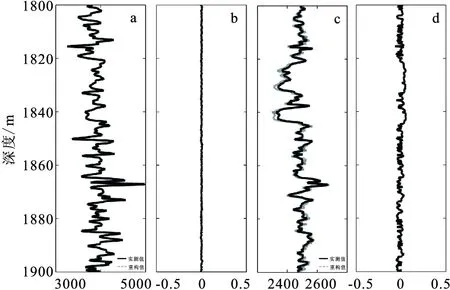
圖11 利用Xu-White模型重構得到的縱橫波 速度及相對誤差Fig.11 Comparison of rebuilt velocity data and measured data using Xu-White model(a) 縱波速度實測值和重構值；(b)縱波速度相對誤差；(c) 橫波速度實測值和重構值；(d) 橫波速度相對誤差

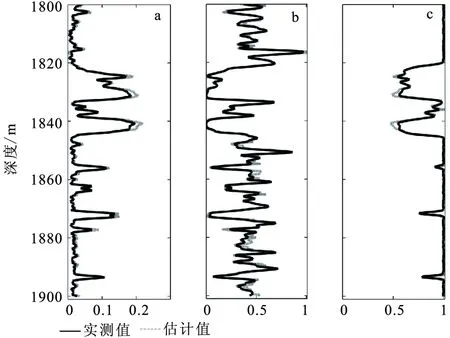
圖12 儲層物性參數的估計結果與實際測量值的對比Fig.12 Comparison of estimated reservoir parameters and the measured data(a) 孔隙度； (b)含水飽和度；(c)泥質含量

將筆者提出的儲層物性參數估計方法應用于中國某油田的實際資料。該工區的儲層是碎屑巖儲層，主要礦物組成是石英和粘土。為了利用測井得到的彈性參數數據估計出儲層的物性參數，首先需要結合巖心實驗等數據建立合適的巖石物理模型并確定模型的基本參數。經研究發現Xu-White模型能夠較好地描述儲層的巖石物理特點。利用Xu-White模型進行地層縱、橫波速度曲線的重構，結果如圖11所示。由圖11可以看出與實際測量值相比，縱波速度的重構值非常準，誤差極小；橫波速度的重構值較為準確，誤差略大于縱波速度的誤差，在1 820 m～1 850 m之間的兩處儲層處誤差相對大一點。但是誤差的絕對值小于5%，精確程度可以滿足儲層物性參數估計的需要。準確的重構結果進一步證明了Xu-White模型對于該工區的儲層是合適的。

基于Xu-White模型進行儲層物性參數的估計。以體積模量、泊松比和密度的測井曲線作為輸入數據，其中密度曲線是實際測井得到的，體積模量和泊松比需要利用實際測井得到的縱橫波速度和密度計算得到。利用本文方法可以得到如圖12所示的儲層物性參數估計結果。通過對比圖12(a)、圖12(b)、圖12(c)以看出，估計結果較為準確，證明方法具有一定的實用性。

4 結論

基于巖石物理理論提出了一種模型約束的巖石物理逆建模方法，可以從彈性參數中同時估計出孔隙度、泥質含量和含水飽和度三種儲層物性參數。在輸入參數沒有誤差的情況下，估計結果是較為準確的；當輸入數據中包含誤差時，由于模型約束可以有效地提高估計結果的穩定性，估計結果的精度也較高。本文儲層物性參數估計方法是在巖石物理建模的基礎上提出的，巖石物理模型的建立至關重要，根據儲層特點建立準確的巖石物理模型有利于得到高精度的估計結果。

附錄

微分等效介質模型(DEM模型)

微分等效介質模型是通過往固體礦物相中逐漸加入包含物相來模擬雙相混合物的。利用微分等效介質模型(DEM模型)計算巖石骨架的模量，等效模量K*和μ*的耦合微分方程分別是：

(A-1)

(A-2)

初始條件是K*(0)=K1，μ*(0)=μ1，其中K1、μ1是基質的體積模量和剪切模量；K2、μ2是逐漸加入的包含物的體積模量和剪切模量，y是包含物的含量，P(*2)和Q(*2)是背景介質中包含物形狀的表達式。

自相容近似模型(SC模型)

自相容近似模型通過用暫時尚未知的有效介質來替換背景介質，以此來近似包含物之間的相互作用，該方法考慮了包含物之間的相互作用，因此可以用于孔隙度較大的巖石。自洽模型公式是由Berryman給出的N相介質混合物的自相容近似表達式：

(A-3)

(A-4)