基于小波包分解的光纖振動特征提取方法

何志勇

（上海海事大學信息工程學院，上海201306）

0 引言

當今社會發展和科技進步十分迅速，與之前傳感器所用材料相比，光纖具有很多優異的性能，以光纖作為傳感器的分布式周界安防系統也就應運而生。為了保證系統具有實時性和有效性，對于信號的特征提取成為了關鍵一步，光纖振動信號特征提取的好壞直接決定了振動信號識別的優劣，由此引起了國內外的重視，也做了大量的研究和實驗。在信號處理中最常用的特征提取算法包括時域分析、頻域分析和時頻域分析[1]。時域分析主要包括時域波形、短時能量、過閾值率等，但如果信號的采樣頻率較低，就不能用時域分析更好地進行處理。而頻域分析主要采用傅里葉變換（DFT）來提取振動信號的頻譜分析方法，但是這種方法也有一定的局限性：傅里葉變換具有較高的頻率分辨率，但是由于其時間分辨率存在弊端的缺點，使其分析非平穩信號時就不太合適。近年來小波包變換受到廣泛關注，它是一種時頻分析方法，它在高頻部分時間分辨率高和低頻部分頻率分辨率高的特點使其在特征提取和信號處理中應用非常廣泛[2]。本文為解決區分無入侵信號和敲擊信號的問題，利用小波包分解提取信號頻域特征，建立能量特征向量，觀察不同頻段的能量分布來發現無入侵信號和敲擊信號的特征，進而達到區分效果。

1 實驗數據

本文研究所用數據是基于φ-OTDR的分布式光纖振動探測系統采集到的數據，該系統輸出的光脈沖周期和脈寬分別為100μs和100ns。以10KHz采樣頻率采集到的數據為一維數據，為了方便分析，將一維數據轉換成“采樣點—位置”的二維數據，實驗開始先選取某個單元作為實驗對象，隨之應用小波包對所取單元開始分解與重構處理，再截取敲擊位置點的數據作為敲擊數據樣本作為特征提取的對象與無入侵位置點的數。

2 小波包分析

2.1 小波包理論

小波變換中的基函數的特性是和尺度有著密切關系的，當尺度增大時，基函數的時寬隨之也會增大，但對應的頻寬會隨之變小[3]。正交小波變換的多分辨率分解只將尺度空間進行分解，高頻點的頻率分辨率是低的但時間分辨率是高的，相反的低頻處的頻率分辨率是高的而時間分辨率是低的，這是正交小波基的不足之處。但小波包有一大優勢能夠彌補這一不足，它能夠通過提高分辨率，將變寬的頻譜窗口分割的更細，進而能將小波空間最大程度的分解[4]。對于給定的信號，通過一組低通濾波器和高通濾波器組合成的正交濾波器組，可以將信號劃分到任意頻段上。

其具體定義為：

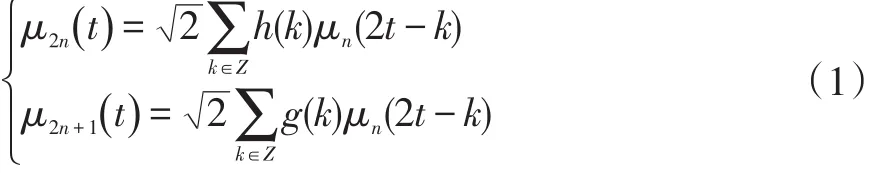
式中所定義的μn(t（)n=1，2，3，…）稱為由正交基函數 μ0(t)=h(t)確定的正交小波包[5]。其中g(k)和h(k)為多分辨分析中的濾波器系數。 μ1(t)=φ(t)。

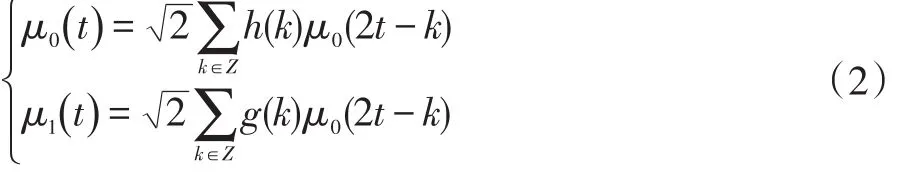
式中：μ0(t)表示正交尺度函數φ(t)；μ1(t)表示小波基函數；φ(t)是通過φ(t)生成的。

2.2 小波包分解

小波包分解是通過把頻帶分成多個層次，將小波分解中簡單劃分的高頻頻段再更細致的分解，意思就是基于在小波分解上再將全頻帶上的信號頻帶做多層次的劃分，然后進行信號特征的分析，利用小波包分解的適應性這一特點去抉擇合適的頻帶，讓它能夠對應于信號頻譜，由此提高了時域與頻域的分辨率，使小波包更具有價值已得到普遍應用。

小波包的分解算法如下:

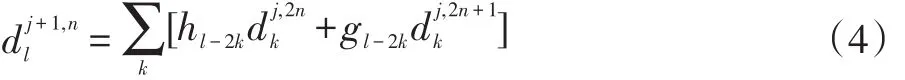
下面以3層小波分解為例進行說明。小波包3層分解結構圖如圖1所示。

圖1中D1,0一層分解低頻部分包含有二層分解DD2,0低頻部分以及GD2,1高頻部分，DD2,0包含三層分解的DDD3,0低頻部分以及GDD3,1高頻部分，以此類推；經過逐層的分解，低頻部分不斷地濾除中、高頻部分，高頻部分也在不斷的細化，通過 GGG3,7、DGG3,6、GDG3,5、DDG3,4、GGD3,3、DGD3,2、GDD3,1、DDD3,0可實現對原信號的重構，分解具有關系：S=DDD3,0+GDD3,1+DGD3,2+GGD3,3+DDG3,4+GDG3,5+DGG3,6+GGG3,7。

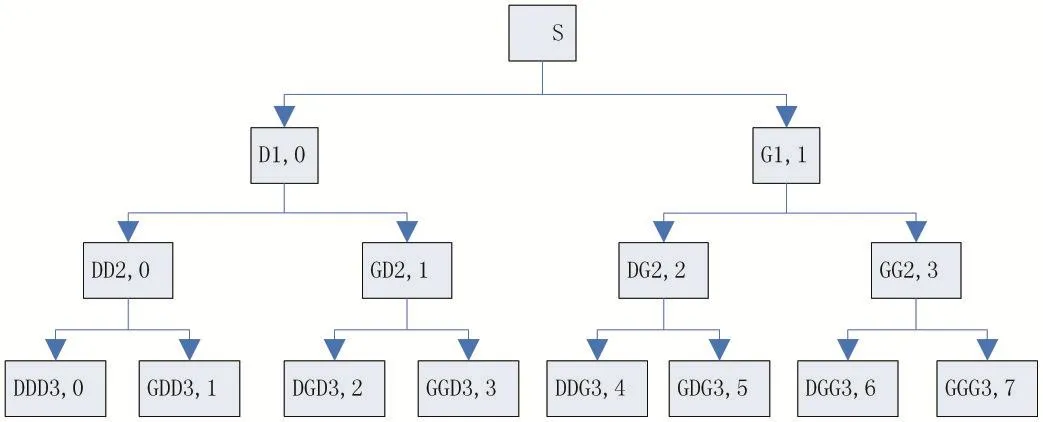
圖1 小波包分解樹結構

對于小波包分解，其中必須要了解的是小波函數。為了仿真達到最佳效果，對于小波基的選擇至關重要，小波基的選擇標準一般從支撐長度、對稱性、消失矩、正則性和相似性著手。這里所需要用到的是Daubechies小波函數，縮寫為db，一般表現形式為dbN，其中N表示小波的階數。則小波函數和尺度函數中的支撐區為2N-1，小波函數的消失矩為N。dbN小波具有較好的正則性，即該小波作為稀疏基所引入的光滑誤差不容易被察覺，使得信號重構過程比較光滑。dbN小波的特點是隨著階次（序列N）的增大消失矩階數越大，其中消失矩越高光滑性就越好，頻域的局部化能力就越強，頻帶的劃分效果越好。綜合考慮，本文對信號進行分解采用的是db2小波包函數。

3 小波包特征提取算法

在小波包分解的過程中，濾波器組每作用一次，數據點數減半。若原始數據長度為2L，分解N次，則每個頻段數據長度變為L/2N-1，是原長的1/2N。如需知道某一頻段內的頻率成分，直接做傅里葉變換不合適[6]。本文所用到的小波包信號特征提取算法，利用了小波包可將信號按任意時頻分辨率分解的特點，將不同頻段的信號正交分解到相應頻段內，并根據先驗知識保留分解序列中任意一個或幾個頻段序列進行重構[7]。重構信號長度仍為2L，具有較窄的頻帶寬度和較高的信噪比[8]。具體算法如下：

（1）對數據進行3層小波包分解，分別提取第3層的8個頻段的頻率成分的信號特征，圖1所示即為該分解結構。其中：

S為原始信號：X00；

D1,0表示第一層第一個節點的系數:X10；D1,1表示第一層第二個節點的系數:X11；

DD2,0：X20；GD2,1：X21；DG2,2：X22；GG2,3：X23；

DDD3,0：X30；GDD3,1：X31；DGD3,2：X32；GGD3,3：X33；

DDG3,4：X34；GDG3,5：X35；DGG3,6：X36；GGG3,7：X37；

（2）對（1）中得到的各個節點的系數進行重構，獲得各個頻率范圍的信號。Xij的重構信號用Sij代表。分析第三層的各個節點，則總信號S可表示為：

假設在待測信號S中，頻率成分范圍是0～1，采用歸一化頻率，則提取的 S3j（j=0，1，…，7）8個頻率成分所表示的范圍見下表。

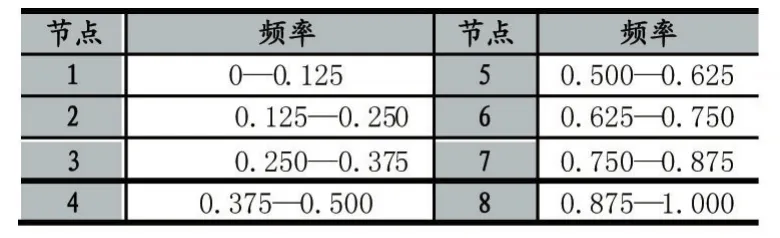
表1 小波包分解后節點對應的頻率范圍

實驗結果顯示，對無入侵信號和敲擊信號小波包分解重構后各節點系數信號圖如圖2所示。

（3）求第三層各頻帶信號的總能量。令各個頻帶信號 S3j（j=0,1,…,7）對應的能量為 E3j（j=0,1,…,7），那么就有：

其中，xjk(j=0,1,…,7)表示重構信號S3j的幅值，m表示分解信號序列S3j的離散點的個數。

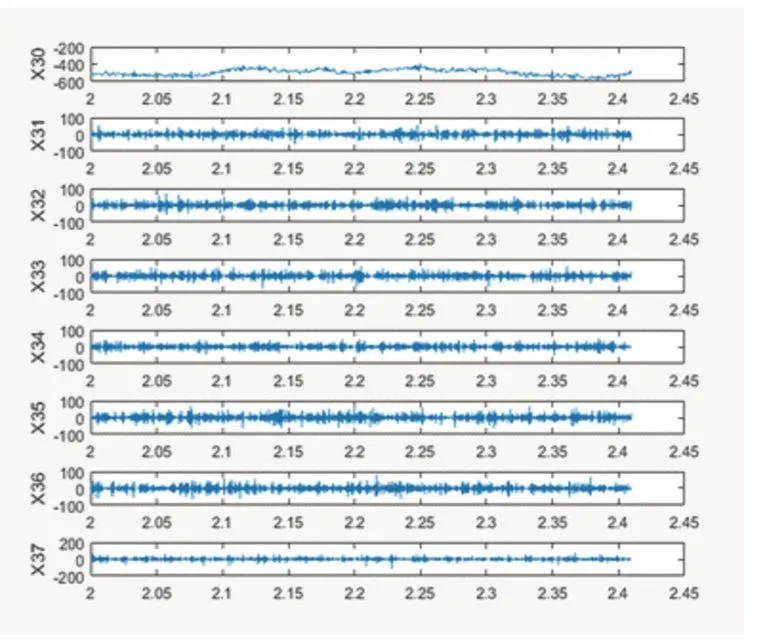
圖2 無入侵信號

（4）構造特征向量。當存在待測信號的時候，處理過程中會對所有頻段中信號的特性造成不小的影響，所以，能夠通過能量建一個用來研究的特征向量。可以將特征向量 T 表示為：T=[E30，E31，E32，E33，E34，E35，E36，E37]。

考慮到當信號能量很大的時候，E3j（j=0,1,…,7）的能量值也可能會很大，所以為了在數據分析上帶來便利，我們選擇先對特征向量進行進一步的處理——特征向量歸一化處理，令：

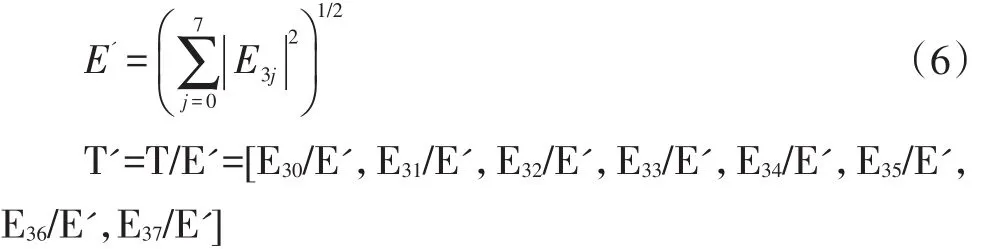
T'即為最后所需進行分析的向量。

4 實驗結果及分析

針對圖4所示仿真信號，分別對其進行時域特征提取、傅里葉變換分析和小波包分析，對所得結果進行對比分析。其中含敲擊信號的開始點位置設為從141開始，單處敲擊142處，全部位置在5.05s-5.4596s內。

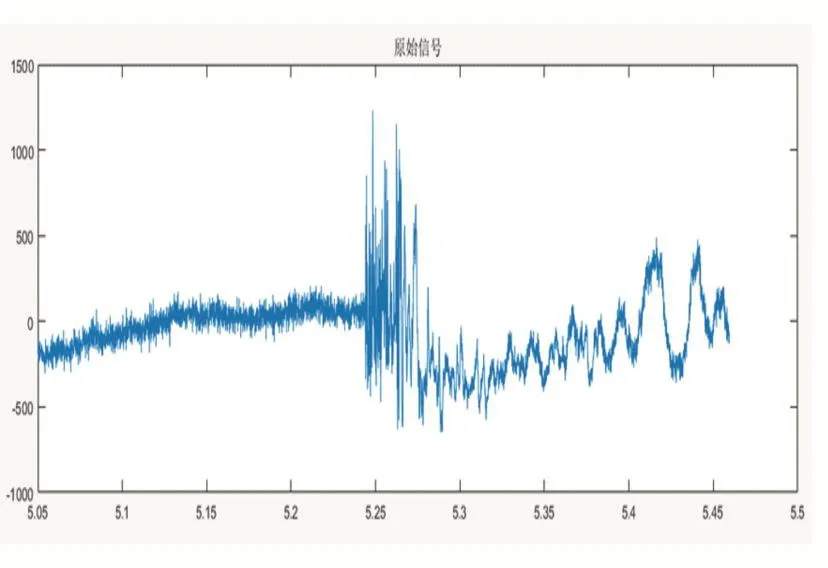
圖4 仿真信號的時域波形

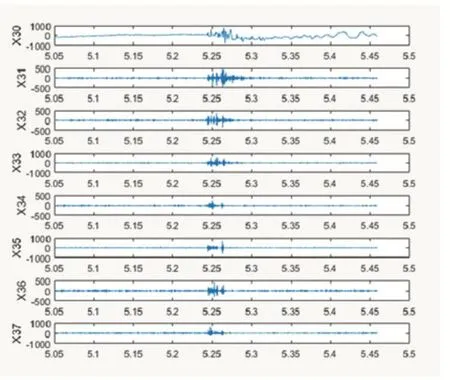
圖3 敲擊信號

通過對比圖5和圖6含敲擊信號和不含敲擊信號的時域特征幅均比計量圖，兩者雖然在各個位置點的比值有所差異，但是區別不是很明顯，尤其是當受到外界因素干擾的時候，更會造成最后檢測結果的異常。

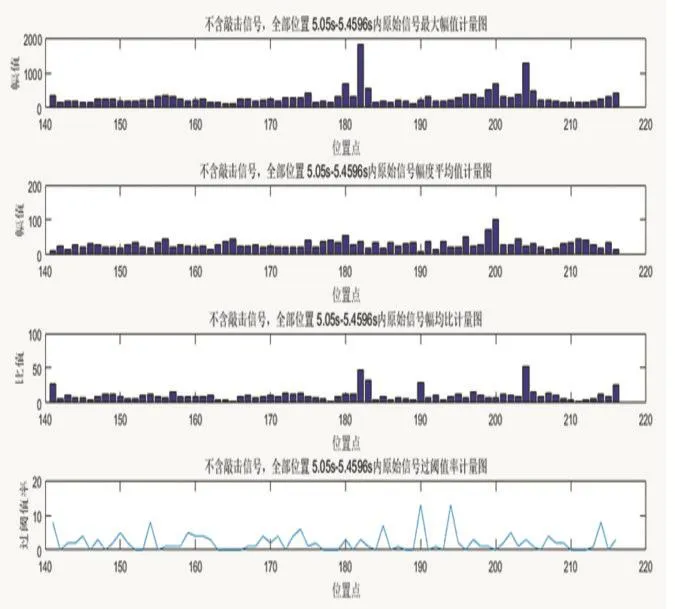
圖5 不含敲擊信號的時域特征提取

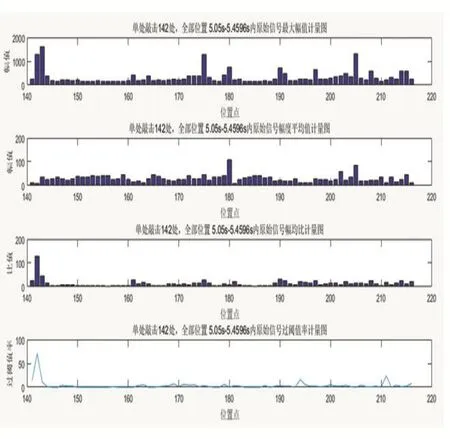
圖6 含敲擊信號的時域特征提取

通過對比圖7和圖8的含敲擊信號和不含敲擊信號頻域特征的歸一化頻率分布直方圖，兩者在各個頻域段的能量分布區別不是很大，而且對于非平穩信號和瞬變信號，傅里葉變換對信號的反映極差，此時的傅里葉變換再用于特征提取就不會有太大的意義。

利用小波包db2對仿真信號進行三層分解，再通過式（5）和（6）分別計算各頻帶歸一化能量，得到能量統計直方圖，獲取各個頻段的歸一化能量如圖4和圖5所示。進行簡單的比較會發現，不含敲擊信號頻段1低頻所占比例幾乎為1，其他頻段所占比例幾乎為0；含敲擊信號的處理結果，雖然頻段1低頻所占比例也很大，但是頻段2～頻段8部分相對較高，這與不含敲擊信號相比具有明顯的區分度，所以本文所用的基于小波包分解光纖振動特征提取方法相較于時域分析和傅里葉變換更具有優勢，是切實可行的。

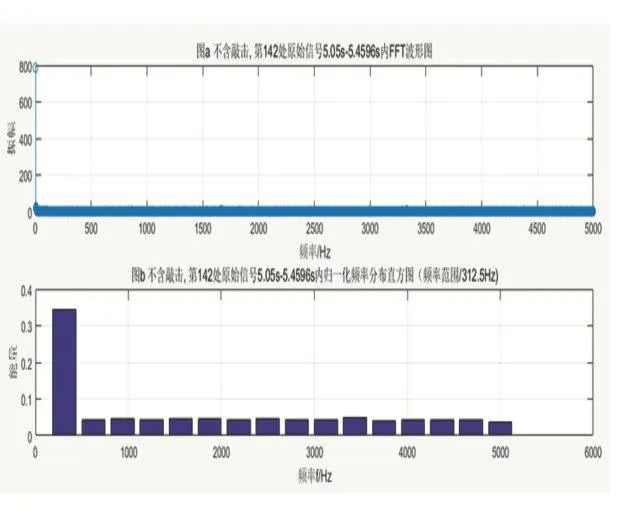
圖7 不含敲擊信號的頻域特征提取

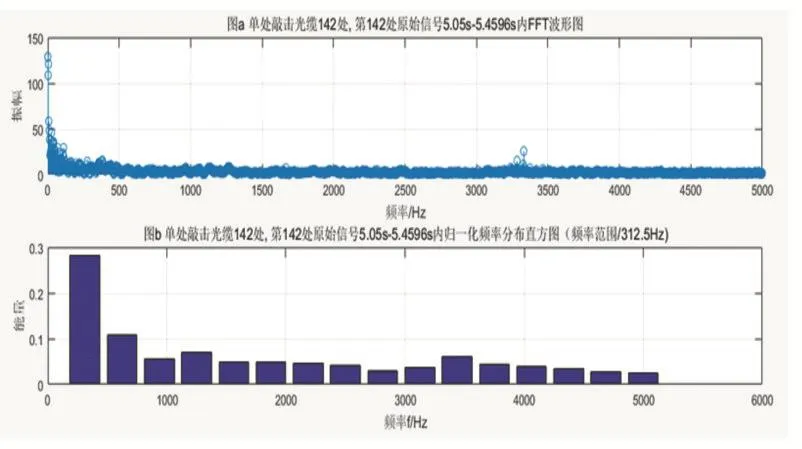
圖8 含敲擊信號的頻域特征提取

5 結語

本文簡單介紹了小波包的理論以及算法流程，利用小波包對含敲擊信號和不含敲擊信號分別進行處理和對比。因為小波包基比一般的小波基具有更高的時頻分辨力，所以該方法能夠提取仿真信號中更為精細的時頻局部信息作為目標的特征，使其識別精度大大提高。由本文實驗結果可以看出，對于含敲擊信號和不含敲擊信號的能量統計直方圖中各頻段所占比例區別十分明顯，所以本文中所用到的特征提取方法能夠有效地解決不同信號的區分問題。同時本文利用的小波包分解提取特征向量的方法為之后更復雜的研究工作提供了基礎，具有較好的參考價值。

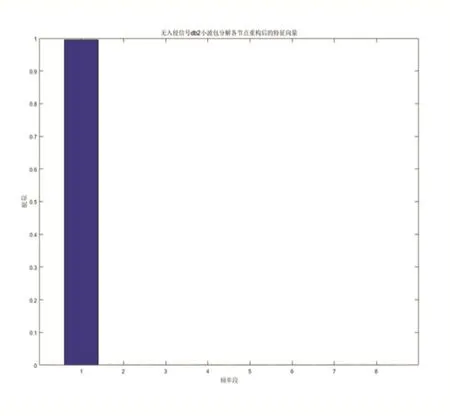
圖9 不含敲擊信號

圖10 敲擊信號

[3]梁瑞勝,孫有田,周希亞.小波包變換和神經網絡的某型導彈故障診斷方法研究[J].海軍航空工程學院學，2008-23(2):217-220.

[4]Ariyani.The Generalized Continuous Wavelet Transform on Hilbert Modules[D].University of New South Wales,2008.

[5]胡昌華，張軍波，夏軍，等.基于MATLAB的系統分析與設計——小波分析[M].西安:西安電子科技大學出版社，1999：20-23.

[6]朱洪俊.非平穩信號瞬時特征提取的諧波小波方法[J].機械工程學報,2008-33(5):191-195.

[7]黃艷芳,張宏斌,仝云崗.基于小波包處理直升機噪聲的研究[C].第二十屆全國直升機年會.宜賓:中國航空學會直升機專業分會,2004:79-83.

[8]許允之,許璟等.基于振動信號分析的異步電機轉子故障特征提取[J].實驗室研究與探索，2012:32-35.