A＊尋路算法的并行化設計及改進

徐唐劍

（江西財經大學軟件與物聯網工程學院，南昌330013）

0 引言

啟發式搜索算法是一種在人工智能等領域中常用的方法。對于人工智能系統來說，問題可能的狀態隨著搜索的深入呈現指數遞增或者階乘遞增，啟發式搜索通過模擬人腦的認知模式，對部分可能的狀態而不是每個可能的狀態進行權衡，找到一個或幾個可能性最大的路徑排除其他可能性較小或為零的路徑，降低算法復雜性。具體的搜索方法就是在搜索過程中不斷評估狀態空間中的每一個狀態，根據其評估值有選擇性地得到相對最優的狀態，然后以這個狀態繼續擴展至最終狀態。常用的搜索算法包括三種：深度優先搜索（Depth-First Search）、廣度優先搜索（Breadth-First Search）、以及最佳優先搜索（Best-First Search）。A*算法是一種基于最佳優先搜索的啟發式搜索算法，其應用取得了不錯的效果。

算法就是一個定義明確的計算過程，在這個計算過程中取一個值或者值的集合作為程序的輸入并產生一個值或者值的集合作為程序的輸出。同時為了更好地解決在生活、工作中遇到的某些問題，有些時候需要對所設計的算法做出優化，如時間復雜度、空間復雜度、正確性和健壯性等方面。而為了讓計算機每秒執行更多的計算，計算機芯片通常被設計成具有多個處理“核”，可以把這些多核計算機當做工作在某一芯片上的幾臺計算機，即“并行計算機”。隨著多核處理器的普及，為了使多核計算機獲得最佳的性能的同時提高程序的運行速度，在設計算法時必須考慮算法的并行性。

1 Dijkstra算法

1.1 算法概述

Dijkstra算法是在1959年的時候由荷蘭的科學家Edsger Wybe Dijkstra提出，它能夠有效解決單源最短路徑問題，該算法要求有向圖中邊的權重都為非負。算法的主要特點是從起點開始不斷向外搜索和擴展，直至達到目標為止，同時在擴展的過程中通過“松弛”操作不斷更新shortest值和pred值，最后在結果中可以得到起點到圖中其他所有結點的最短路徑及其權重和。通過簡單的數組實現的Dijkstra算法，那么它的時間復雜度是O（n2）。但采用更優的數據結構實現的話，如使用斐波那契堆實現的Dijkstra算法，它的時間復雜度可以達到O（nlgn+m）。

1.2 算法思想

Dijkstra算法中最關鍵的部分是維護結點集S。算法不斷從結點集Q中選取具有shortest最小的結點u，將結點u加入到結點集S，然后對所有與該結點有關的邊進行松弛操作。Dijkstra算法每次都是從結點集Q中選取與結點u“最近”的結點加入到結點集S中，這是一種典型的貪心策略。但不是使用貪心策略一定能夠獲得最優解，但是可以通過一些定理和推論可以證明Dijkstra算法的解確實是最優解。

（1）松弛操作

首先將從起點到結點u的所花費最短路徑的值與邊（u,v）的權重之和與起點到當前結點v所花費的最短路徑值進行比較。如果加上邊（u,v）的權重得到的值更小，那么需要將shortest[v]的值更新為當前shortest[u]+weight（u,v），并且將最短路徑上結點v的前驅設置為結點u。

程序RELAX（u,v）

輸入：邊（u,v）的頂點 u,v

結果：

如果shortest[v]的值減小了，那么令pred[v]取u。

如 果 shortest[u]+weight（u,v）＜shorest[v]，那 么 將shortest[v]賦值為shortest[u]+weight（u,v），同時將pred[v]賦值為u。

（2）算法步驟

Dijkstra算法通過重復對具有最小shortest值的結點相關聯的每條邊執行松弛操作來工作。首先，需要將有向圖中所有結點加入結點集Q，然后還需要唯一確定一個源點s，并將shortest[s]的值初始化為0，對于圖中其他所有頂點v的shortest[v]值設為無窮大，對所有結點的pred[v]值將其設為NULL，算法不斷從結點集Q中選取具有shortest最小值的結點u，并將該結點從結點集Q中移除，再對所有與結點u相關的邊執行松弛操作。

程序DIJKSTRA（G,s）

輸入：有向圖G、源點s

結果：對于有向圖G中的任何一個非源點v，shortest[v]的值指的是從源點s到結點v的最短路徑上所有邊的權重和。pred[v]表示在最短路徑上結點v的父結點。對于源點，將其shortest[s]的值置為0,pred[s]的值置為NULL。規定如果從源點s與結點v不存在路徑，那么shortest[v]的值是無窮大，而pred[v]的值是NULL。

①初始化。將除起點s以外的任何結點v的shortest[v]值設為無窮大，其pred[v]的值設為NULL。然后將 shortest[s]的值置為 0，pred[s]置為 NULL。

②將所有的結點加入結點集Q。

③只要結點集Q不為空：

A.在結點集Q中選取一個具有shortest[u]最小值的結點u，然后將這個結點從結點集Q中移除。

B.找出每個與頂點u鄰接的結點v：

執行松弛操作，即調用RELAX（u,v）。

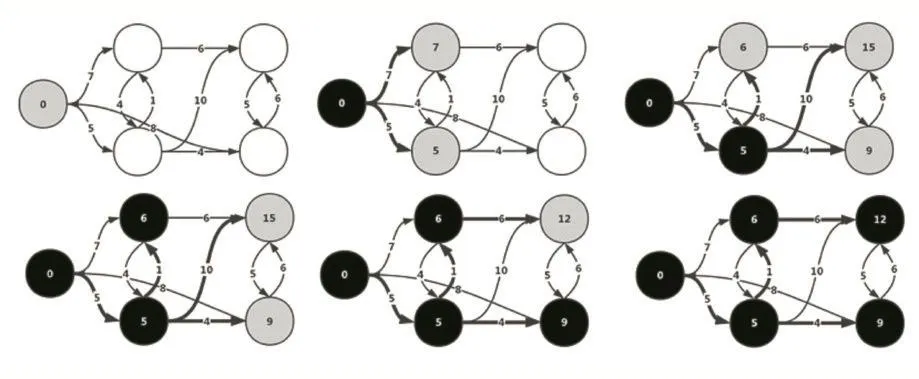
圖1 Dijkstra算法運行流程圖

（3）核心代碼

Python是一種面向對象的解釋型計算機程序設計語言，于1989年由Guido van Rossum發明。Python具有豐富庫而且這些庫的功能強大，由于它可以與其他語言很好的合作所以常被稱為“膠水語言”。近些年來，尤其是人工智能逐漸成為人們關注的重點，而其首選編程語言就是Python。其次Python在網絡爬蟲方面的運用也是非常廣泛的，加上其“優雅”、“明確”、“簡單”的設計特點，Python得到了大多數人的青睞。Python于2017年7月在IEEE發布的編程語言排行版位居首位。為了適應互聯網時代發展的要求，本文使用了Python作為算法實現的主要編程語言，以下是Dijkstra算法實現的核心代碼：

2 A＊算法

2.1 算法概述

2.2 算法思想

A*算法是建立在經典Best-First Search和Dijkstra算法的基礎上的一種啟發式搜索算法，算法通過引入評估函數減少搜索范圍和降低空間復雜度。通常將評估函數定義為：

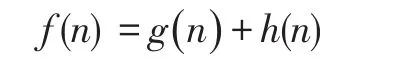
g（n）表示從起點到當前點n的實際移動距離，即從起點移動到當前點n所花費的移動代價。h（n）表示從當前點n到終點或目標點的估算距離，即對當前點n移動到終點的估算移動代價。通過比較評估函數f（n），選取具有最優值的結點用作下一次的擴展。

（1）算法特性

①當只計算g（n）時，即只計算和考慮起點到當前點n的實際耗費距離，不考慮當前點n到終點的估算耗費距離。那么算法就會被轉換為經典的Dijkstra算法，此時需要考慮所有位置的狀態。

②當只計算h（n）時，即只計算和考慮當前點n到終點的估算耗費距離，不考慮起點到當前點n的實際耗費距離。那么算法就會被轉化為使用貪心策略的Best-First Search，速度最快，但是可能得不到實際最優的解。

③如果估算距離不高于實際距離，即h（n）不高于g（n），那么算法則一定可以得到最優解。常見的估算方法有：歐幾里得距離、曼哈頓距離以及切比雪夫距離。

（2）算法步驟

A*算法一般通過Open和Closed兩張表維護在搜索過程中擴展得到的結點。將擴展得到的且有效的結

A*算法是目前來說最有效的一種直接搜索算法，同時也是目前常用的一種啟發式搜索算法（Heuristically Search）。該算法由 Peter Hart、Nils Nilsson和 Bert ram Raphael三人于1968年在斯坦福研究院提出。A*算法是對Dijkstra算法的一個擴展，同時也是一種高效的搜索算法。A*算法運用非常廣泛，可以在游戲領域看到它的身影，如NPC移動計算。點置入Open表，將已經搜索過的結點置入Closed表。具體算法可描述如下：

步驟1初始化Open表和Closed表；

步驟2將起點A加入到Open表，此時待搜索的結點只有一個，即起點A的估價值肯定為最優值；

步驟3若Open表非空，則取出具有評估最優值的結點，進行下一步操作，否則跳轉至步驟8；

步驟4將具有評估最優值的結點n取出，并將這個結點加入到Closed表中，如果結點n就是終點B或者就是最終狀態，那么跳轉至步驟8，否則進行下一步操作；

步驟5對結點n進行擴展，即取與結點n相鄰且滿足未在Closed表中、非不可操作等條件的結點N1至Nt；

步驟6對結點N1至Nt進行評估，即計算起點A到當前結點的實際移動距離和當前結點到終點B的估算距離之和；

步驟7將結點n作為N1至Nt的父結點，并將N1至Nt加入到Open表中，跳轉至步驟3；

步驟8根據父結點進行回溯生成最短路徑，銷毀Open表和Closed表，程序結束。

圖2 A*算法運行結果圖

（3）核心代碼

根據實際的需求選擇選擇下一步可以移動的位置，通常在2D游戲中下一步通常可以有八個可以移動的方向，當然也可以設置只有四個可以移動的方向。同時根據障礙物，可以設置相應的規則，如當前結點的右鄰有障礙物時，規定當前結點的右上、右、右下三個方向是不可行的。

3 雙向A＊算法

3.1 算法概述

通過對傳統A*算法進行實現和分析，發現其實際運行時間性能較差且存在一些缺點，很難滿足實際運用的需求。可以通過對其搜索方式進行改進和設計，使其滿足實際需求。與傳統A*算法不同的是，傳統A*算法使用的搜索方式為從起點一直搜索擴展到終點為止，由在此過程中生成一條最短路徑。而雙向A*算法采取的搜索方式是從兩個方向同時進行搜索，即一個從起點向終點擴展，另一個從終點向起點擴展。當兩個搜索路線匯合到同一個位置時，就可以得到一條最短路徑。

3.2 算法思想

雙向A*算法的主要思想是：傳統A*算法的搜索結果會在圖上呈現為一個扇形展開的樹結構。而一個大的搜索樹的搜索展開速度遠遠不如兩個較小的搜索樹，使用兩個較小的搜索樹在一定情況下可以加快算法的運行速度。同時對傳統A*算法引入并行化設計，滿足時代發展要求，即符合如今多核計算機已經非常普及的現狀。

在理想情況下，雙向A*算法的運行速度相比于傳統A*算法的運行速度將會提高一倍，理想運行過程如圖3所示：

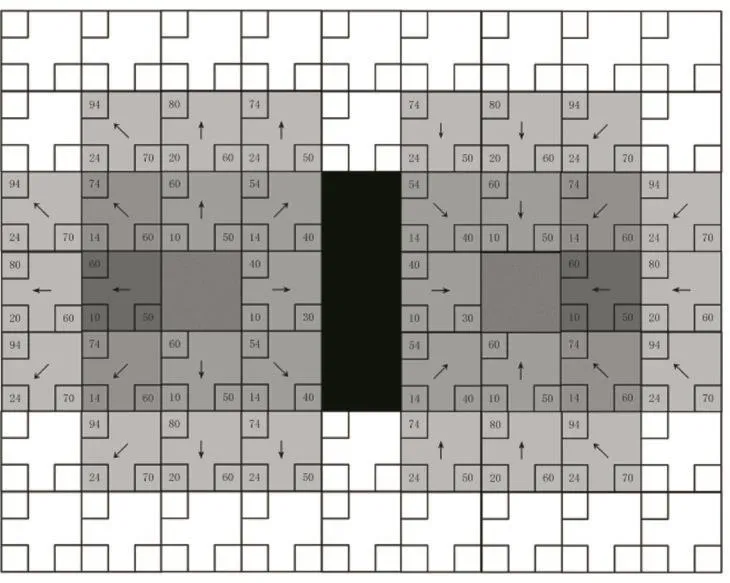
圖3 雙向A*算法理想情況下的運行流程圖

（1）核心代碼

雙向A*算法通過開啟兩個線程執行兩個不完全相同的搜索過程，即一個線程處理從起點到終點的搜索過程，另一個線程處理從終點到起點的搜索過程。當兩個線程處理到同一個結點時，以此可以判定算法已經找到一條最短路徑。

（2）雙向A*算法實際運行情況

通過實際運行對比，可以發現雙向A*算法的運行速度在復雜路徑問題的求解中的運行效率是高于傳統A*算法的。另外，傳統A*算法在求解復雜路徑問題是往往只能得到一個固定的解，而雙向A*算法在某些路徑問題的求解過程中可以得到實際存在的多個不同最優解。

傳統A*算法和雙向A*算法在某個特定路徑問題中求解情況如下（小括號內為算法運行時間）：

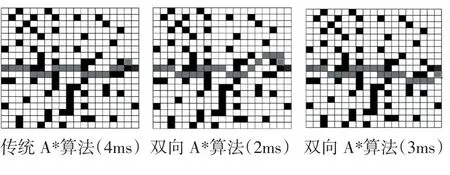
圖4

4 其他改進方法

4.1 定向搜索

在傳統A*算法的搜索過程，Open列表用于保存可能需要被擴展的結點。定向搜索是在傳統A*算法的基礎上，通過限制Open列表的大小而得到一種改進方法。這種改進方法的好處是，當Open列表太大時即待搜索的結點太多時，會將可能性最小的即評估值最低的節點排除，從而一定程度上減少了算法的搜索空間。但這種改進方法會帶來一定的缺陷，即需要對Open列表進行篩選所以對數據結構的選擇增加了限制條件，同時這種改進方法可能會得到不到最優解，即無法找到實際最短路徑。

4.2 動態加權

該改進方法假定需要在搜索開始時快速達到某個狀態或位置。通過一個權值w（w＞=1）和估算函數相關聯。在不斷接近終點時，權重w的值也不斷減少，通過這種改進方法可以降低在對某個狀態評估時估算函數的重要性，提高實際花費代價的重要性。算法的思想為搜索前期以搜索速度為重點，搜索后期重點考慮搜索正確率。

4.3 雙向搜索變體

為了繼續對雙向A*算法的性能等方面進行優化和改進，眾多文獻討論了不同的方法。

重定向方法不同于一般雙向搜索算法，這種方法放棄了完整的前向搜索或者后向搜索，首先從起點開始進行一次短暫的前向搜索并選取一個最佳的前向候選結點。然后進行后向搜索，不同于完整的后向搜索。此次后向搜索的起始結點為終點，目標點為上一步選擇的前向候選結點，這個搜索過程也不是完整的，同樣也可以得到一個最佳的后向候選結點。接著從前向候選結點向后向搜索結點繼續進行擴展，重復這個過程，直到前向搜索結點與后向搜索結點匯合。

面對面方法通過將前向搜索的結果和后向搜索的結果整合在一起。即評估函數滿足以下公式：

5 結語

A*算法是廣泛應用在圖論、人工智能、智能控制領域的一種啟發式搜索算法。但是由于在很多情況下它的搜索狀態空間非常龐大從而導致其運行及搜索效率不高，所以傳統的A*算法并不能在實際生活和工作中得到有效的應用。通過對A*算法引入并行化技術，可以有效減少其運行時間。目前有很多文獻對A*算法的優化提出了解決方案，這些方案也成功運用在各個領域，改進后的A*算法可以更好地解決在工作和生活中遇到的路徑問題。