從歷史發(fā)展的視角看中學概率教學

張蜀青，曹廣福，羅荔齡

?

從歷史發(fā)展的視角看中學概率教學

張蜀青1，曹廣福2，羅荔齡2

（1．廣州市執(zhí)信中學，廣東 廣州 510095；2．廣州大學 數(shù)學與信息科學學院，廣東 廣州 510006）

按照歷史發(fā)展的脈絡，從古典概型到統(tǒng)計意義下的概率，再到公理化的概率論，對概率論的發(fā)展做了簡明扼要的闡述，方便一線教師對概率論基本歷史有一個初步的了解．同時，通過一系列問題情境的創(chuàng)設，針對中學一線課堂中隨機事件、樣本空間、古典概型與幾何概型等概念的教學提出了具有可操作性的建議．概率教學應遵循幾個基本原則：（1）適應學生的認知水平；（2）在尊重歷史的基礎上改進教學內(nèi)容；（3）杜絕偽情境．概念的定義應該準確，不同概念之間（基本事件、樣本空間、隨機事件等）的邏輯關系應該清晰明了．中學階段不宜設計一些類似貝特朗問題的陷阱，這些問題除了增加學生對幾何概型理解的困難，并不能為學生學習概率帶來更多的幫助．

隨機事件；樣本空間；幾何概型；古典概型；隨機變量

1 引言

概率是中學數(shù)學的重要組成部分，也是中學數(shù)學教學中的難點，之所以難，主要原因或許來自兩個方面：一是很多中學教師對概率論了解不多，有些甚至沒有學過概率論；二是一些教材對概念的闡述不夠清晰，導致理解上的困難．中學教材首先從頻率的角度定義概率，將概率定義為重復隨機試驗中頻率的極限，然后回到古典概型．統(tǒng)計意義下的概率定義是存在邏輯問題的，而且，中學階段雖然學習微積分，但并不介紹極限概念，教學過程中也很難實現(xiàn)從頻率到概率的極限過度，一些教師通過拋硬幣或計算機模擬的方法引入概率概念，但顯得很不自然，而且任何有限次重復試驗的頻率與概率都可能相去甚遠．所以概率的教學是個值得好好研究的課題．

2 概率論簡史

在研究教法之前，首先需要了解一下概率論的前世今生，不清楚其來龍去脈，教學有如盲人摸象．

2.1 賭徒梅累的問題

概率論出身“卑微”是眾所周知的，它很長一段時間得不到數(shù)學家們的普遍認同與它的出身或許有一定關系．但更重要的是，早期的概率論缺少嚴格的數(shù)學基礎，這恐怕是概率論很長時間不能登堂入室的根本原因．一些數(shù)學史甚至沒有把概率論列入其中，例如M·克萊因的《古今數(shù)學思想》[1]甚少提及概率論，這也許與這套巨著偏重于確定性數(shù)學有關．

擲骰子始于什么時候無從考證，但數(shù)學家研究這個問題還是有據(jù)可查的，發(fā)明了一元三次方程求根公式的16世紀意大利數(shù)學家卡爾丹（1501—1576）同時也是個賭徒，他曾說過一句：“誠實的骰子”，意思是說，擲骰子是公平的，機會均等，這是古典概型的基本前提．但擲骰子作為一個學術問題被數(shù)學家們研究可能最早開始于17世紀中葉，據(jù)說法國數(shù)學家帕斯卡（Blaise Pascal，1623—1662）在度假旅途中偶遇賭徒梅累，梅累向帕斯卡提出了一個分賭注的問題．梅累向帕斯卡介紹說，他在一次與賭友擲骰子時，每人押了32個金幣，并事先約定：如果梅累先擲出3個6點，或其賭友先擲出3個4點，便算贏家．然而當梅累擲出兩次6點，賭友擲出一次4點時梅累接到通知，要他馬上陪同國王接見外賓，賭博不得不中斷，但就此收回各自的賭注心有不甘，于是決定按照已經(jīng)取得成績分取這64個金幣．但梅累與賭友不知道該如何分配這筆賭注．帕斯卡告訴梅累：如果再擲一次，甲勝，甲獲全部賭注，乙勝，甲、乙平分賭注，兩種情況可能性相同，所以這兩種情況平均一下，甲應得賭金的3/4，乙得賭金的1/4．帕斯卡的回答或許讓人一時難以理解，費馬則給了一個令人信服的解答．首先把問題簡化一下：甲、乙兩人同擲一枚硬幣，規(guī)定若正面朝上，則甲得一點，若反面朝上，則乙得一點，先積滿3點者贏取全部賭注．假定在甲得2點、乙得1點時，賭局由于某種原因中止了，問應該怎樣分配賭注才算公平合理．費馬認為：結束賭局至多還要2局，結果為4種等可能情況：

情況 1 2 3 4

勝者 甲甲 甲乙 乙甲 乙乙

前3種情況，甲獲全部賭金，僅第4種情況，乙獲全部賭注．所以甲分得賭金的3/4，乙得賭金的1/4．顯然費馬的解答比帕斯卡的解答更容易理解一些．

2.2 古典概型

帕斯卡與費馬雖然并未在研究這類問題時給出明確的定義，他們只是定義了使某賭徒取勝的機遇，也就是贏得情況數(shù)與所有可能情況數(shù)的比，這實際上就是后來人們定義的概率．對賭博問題感興趣的人不只是帕斯卡與費馬，1655年，荷蘭數(shù)學家惠更斯在巴黎時了解到帕斯卡與費馬的工作，也興味盎然地參加討論，這就是《關于賭博中的推斷》（1657年）一書的由來，它是早期概率論的奠基之作．直到19世紀初，人們關于概率的研究大多限于古典概型，法國數(shù)學家拉普拉斯（1749—1827）在他的《概率的分析理論》一書中是這樣定義概率的：“事件A的概率等于一次試驗中有利于事件A的可能結果數(shù)與該事件中所有可能結果數(shù)．”古典概型有兩個基本特征：（1）可能結果總數(shù)是有限的，用現(xiàn)在的語言敘述就是“樣本空間”有限；（2）每個結果的出現(xiàn)有著同等的可能性，或者說樣本空間中的點是等可能的．

由于貝特朗問題的出現(xiàn)使得人們對拉普拉斯的古典概型定義大肆抨擊，這對拉普拉斯實在有點不公正，貝特朗問題研究的是無限樣本空間情形，拉普拉斯說的是樣本空間有限的情形，把貝特朗奇論的罪過歸到拉普拉斯頭上有點莫名其妙．在樣本空間有限的情形，拉普拉斯的定義并無什么問題，否則類似擲骰子問題就不存在公平了，正如賭場出老千一樣，在骰子里灌鉛，或者在桌子下面放磁鐵，擲骰子或轉盤出現(xiàn)的數(shù)字顯然就不是等可能的了，事實上，貝特朗問題在古典概型中是不會出現(xiàn)悖論的．貝特朗問題出現(xiàn)悖論是由于關注了隨機試驗結果的不同屬性從而導致不同度量所帶來的，而非樣本空間的等可能性假設不同所致．這里不妨以擲骰子為例，假設骰子出現(xiàn)6個面是等可能的，也就是出現(xiàn)1到6六個數(shù)字的可能性是相同的，人們通常認為，相對于這個隨機試驗的所有可能結果即樣本空間應該是{1, 2, 3, 4, 5, 6}，其中各個數(shù)字的出現(xiàn)是等可能的，所以每個數(shù)字出現(xiàn)的概率都是1/6．如果要計算出現(xiàn)某幾個數(shù)字的概率，直接用出現(xiàn)這些數(shù)字的可能結果與結果的總數(shù)去比就可以了，例如出現(xiàn)偶數(shù)的概率與出現(xiàn)奇數(shù)的概率都是1/2．但如果機械地理解古典概型與隨機試驗的樣本空間就會導致貝特朗問題的爭論．

假設立方體（骰子）的6個面分別標注1至6六個不同的數(shù)字，只要立方體的材質密度分布均勻，出現(xiàn)6個數(shù)字的可能性可以認為是相同的，這也叫無差別原則．這時的樣本空間為{1, 2, 3, 4, 5, 6}，如前所述，可以計算出出現(xiàn)奇數(shù)的概率與出現(xiàn)偶數(shù)的概率均為1/2．現(xiàn)在換一種說法，把1、3、5三個數(shù)字用黑色的顏料涂抹掉，將2、4、6三個數(shù)字用白色的顏料涂抹掉，隨機擲這個只有黑白兩色的骰子，出現(xiàn)每個面的可能性是相同的，這時的樣本空間是什么？顯然是{黑色，白色}，出現(xiàn)黑色的概率與出現(xiàn)白色的概率均為1/2．除了把六面體的數(shù)字用黑白兩色涂抹掉，骰子的隨機性并沒有發(fā)生改變，但樣本空間卻不同了．人們通常認為{1, 3, 5}是一個隨機事件，其概率可以根據(jù)1、3、5出現(xiàn)的概率來計算，3個點的概率相加，自然是1/2．

在一個隨機試驗中，可能出現(xiàn)具有多種屬性的結果，如果你關心的某種屬性沒有共性，那么所有可能的結果都是樣本點，如果你關心的某種屬性具有共性，也可以將具有共同屬性的結果放在一起作為樣本點．上面的隨機試驗說明，當你關心的是骰子的每一面出現(xiàn)的具體數(shù)字，而這些數(shù)字又是互不相同的，那么樣本空間就是可能出現(xiàn)的每一個數(shù)字，例如上面的{1, 2, 3, 4, 5, 6}．如果關心的是這些數(shù)字的某種共同屬性，例如奇偶性，那么可以將這種共同的屬性作為可能的結果，即樣本點，具體地說，如果上面擲骰子試驗關心的是數(shù)字的奇偶性，那么樣本空間可以看成{{1, 3, 5}, {2, 4, 6}}或者{奇數(shù)，偶數(shù)}．這里蘊含著分類的思想，將同為奇數(shù)的數(shù)字放在一起看成一點，同為偶數(shù)的數(shù)字放在一起也看成一點．這就是分類的思想，即將奇數(shù)與偶數(shù)各自分成一類．如果不理解分類思想，就無法理解貝特朗問題的3種不同解答．

即使是樣本空間有限的情況下關注隨機試驗結果的不同屬性也可能導致不同的概率問題．以摸球問題為例，假設箱子里有7個分別標注有1到7不同數(shù)字的球，形狀、大小、質地都一樣，隨機從箱子里摸一只球，出現(xiàn)每個數(shù)字的概率都是1/7．如何計算出現(xiàn)奇數(shù)與偶數(shù)的概率？一種方法是傳統(tǒng)的，把奇數(shù)偶數(shù)都看成樣本空間的子集，即隨機事件，然后計算其概率，另一個辦法與前面類似，把7個數(shù)字按奇數(shù)與偶數(shù)分類，則得到樣本空間{奇數(shù)，偶數(shù)}，但這時候的樣本點顯然不是等可能的，出現(xiàn)奇數(shù)的概率為4/7，出現(xiàn)偶數(shù)的概率則為3/7，按定義，這就不是個古典概型．由此可見關注隨機試驗結果的不同屬性可能導致不同的概率問題．但對于有限的樣本空間來說，只要隨機假定是一樣的，無論采用哪種方法，不會出現(xiàn)不同的答案，也就是說不會產(chǎn)生類似貝特朗問題的悖論．這是因為有限樣本空間中的度量方法是統(tǒng)一的，都是計算所有可能結果的數(shù)量．這個問題對于實際生活有意義嗎？其意義是不言而喻的．例如，工商管理部門要抽檢市場上幾個不同品牌的同類產(chǎn)品，如何抽取樣品？比較公平合理的做法是根據(jù)各品牌投放市場的總量按比例抽取一定數(shù)量的樣品，這樣得到的合格率才是客觀可信的．舉例來說，廠商甲投放了100萬件，廠商乙投放了50萬件，這時工商部門分別從兩個品牌中各抽檢1?000件顯然是不合理的．

2.3 統(tǒng)計意義下的概率定義

古典概型要求樣本空間是有限的，雅各布·貝努利認為：“這種方法僅適用于極罕見的現(xiàn)象．”他主張通過觀察來確定結果數(shù)目的比例，這或許可以認為是統(tǒng)計意義下概率的早期定義．貝努利說：“即使是沒有受過教育與訓練的人，憑天生的直覺，也會清楚地知道，可利用的有關觀測的次數(shù)越多，發(fā)生錯誤的風險就越小．”在古典概型下，貝努利證明：“當試驗次數(shù)越來越大時，頻率接近概率．”這個論點不僅適用于古典概型，也適用于更一般的情形，1919年，德國數(shù)學家馮·米塞斯（1883—1953）在其《概率論基礎研究》一書中提出了概率的統(tǒng)計意義上的定義：“在做大量重復試驗時，隨著試驗次數(shù)的增加，某個事件出現(xiàn)的頻率總是在一個固定數(shù)值的附近擺動，顯示出一定的穩(wěn)定性，把這個固定的數(shù)值定義為這一事件的概率．”這個定義的確擺脫了“等可能性”假設的束縛，它適用的范圍更廣泛．

然而，等可能性假設并非一個脫離經(jīng)驗的單純主觀假設，焉知擲骰子出現(xiàn)各個數(shù)字是等可能的假設不是一個統(tǒng)計意義下的結果？賭場規(guī)則雖然是一種人為的約定，但這樣的約定要得到廣大賭徒的認同必定有基于經(jīng)驗的成分，正是在多次擲骰子的重復試驗中發(fā)現(xiàn)了這樣的規(guī)律．也就是說，拉普拉斯關于古典概型的定義應該也是基于人的直覺，并非拉普拉斯的主觀約定．正如一個箱子里有7個球，其中4個黑色，3個白色，只要7個球外形、大小都是一樣的，隨機從箱子里摸球，不可能有人認為出現(xiàn)黑色與出現(xiàn)白色的概率相同，這不是基于理論的推導，而是經(jīng)驗判斷．

中學階段雖然不學一般意義下的概率，但教師在介紹頻率與概率的關系時至少應該向學生說明幾個問題：（1）“頻率接近概率”只有在樣本量非常大的情況下才有意義，任何有限的實驗數(shù)據(jù)中，其頻率與概率很可能相距甚遠．（2）很多概率的估算可能不是大量重復試驗的結果，例如炮彈合格的概率不可能根據(jù)頻率來估算，只能是通過有限的試驗再結合工程師的經(jīng)驗以及制造炮彈的各種參數(shù)來判斷．再如天氣預報一般也并非根據(jù)某種氣象出現(xiàn)的頻率來估算該現(xiàn)象出現(xiàn)的概率是多少，而是根據(jù)各種氣象數(shù)據(jù)綜合分析得出的結論．

2.4 公理化的概率論

（1）公理化概率論的緣起．

在公理化概率論誕生前，概率論一直遭人詬病，以至于始終不能為數(shù)學家們普遍接受．1900年的國際數(shù)學家大會上，希爾伯特（1862—1943）提出的23個著名問題中，建立概率論的理論基礎便是其中之一（希爾伯特第六問題），但希爾伯特沒有將它放在數(shù)學類，而是放在數(shù)學物理類．

自從希爾伯特倡議建立概率論的公理化基礎之后，很多數(shù)學家開始為概率論尋找它作為數(shù)學而“存在”的理由．數(shù)學史上完全從不同的角度研究同一類問題或者研究不同的問題卻采用了類似方法的例子十分常見．就概率論而言，它最終能堂而皇之走進數(shù)學殿堂成為數(shù)學的一個重要分支跟那個時期數(shù)學的發(fā)展有著密切關系．很難想象，如果沒有勒貝格（Lebesgue，1875—1941）發(fā)明的測度論（雖然這之前關于測度的研究已經(jīng)有很多，特別是波萊爾測度對數(shù)學的影響很大，迄今依然經(jīng)常為人們使用，但都很不完善，波萊爾的學生勒貝格的工作幾乎取代了前人所有的工作），還能有后來柯爾莫哥洛夫（Kolmogorov）的偉大工作．20世紀30年代，柯爾莫哥洛夫正是基于測度論為概率論建立了一套公理體系，從而給一直不能跨進數(shù)學之門的概率論奠定了嚴密的數(shù)學基礎，使得概率論成為數(shù)學殿堂中名正言順的一員．

試圖對中學生講清楚公理化概率論恐怕是一件異想天開的事，即使是曾經(jīng)在大學學過概率論的中學教師，他們中的大多數(shù)人可能也不清楚公理化概率論為何物，因為早期大學的概率論教材很多并不介紹公理化的概率論，僅僅局限于微積分意義上的連續(xù)型分布，其分布密度函數(shù)是一個非負的黎曼可積函數(shù)．但作為教師，不了解概率論的前世今生而去教概率論似乎是一件不可思議的事情，事實上，經(jīng)典的幾何概型不僅存在類似貝特朗問題的理解上的歧義，概念也是很不嚴謹?shù)模@里采用通俗的方式介紹一下什么是公理化的概率論，以便讀者對這一理論有一個大概了解，從公理化的概率論便可以看出幾何概型的漏洞在哪里．

回顧一下，無論是古典概型還是幾何概型，計算隨機事件的概率時都需要采用合適的度量方法去測量樣本空間子集的大小．古典概型使用的是計數(shù)方法，即用隨機事件可能的結果數(shù)量去比所有可能結果（樣本空間）的數(shù)量．幾何概型情形下樣本空間是無限的，用隨機事件可能的結果數(shù)量作為度量顯然是沒有意義的．所以需要使用不同的度量方法，一維情況下使用長度，二維情況下則使用面積．無論是古典概型使用隨機事件可能結果的數(shù)量還是幾何概型中使用長度或面積，他們都有一些共同的特點．不妨用X表示樣本空間（有限或無限），E表示隨機事件（樣本空間的子集），(E)表示隨機事件E的概率，那么(E)有這樣幾個特征：

（1）對任意X的子集E，有(E)≥0，(ф)=0；

（2）(X)=1；

（3）如果E、F是X中兩個互不相交的子集，則(E∪F)=(E)+(F)．

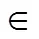
(∪=1∞E)=Σ=1∞(E)？

這個等式稱為可數(shù)可加或可列可加．可以證明，如果可加性恒成立，那么可數(shù)可加性必定也成立，有興趣的讀者要證明這件事并不困難，或者可以從任何一本實變函數(shù)書籍中找到答案．因此問題的關鍵是可加性是否恒成立？或許你以為這個問題再平凡不過，先別急于下結論，姑且回頭來重新審視一下樣本空間及其隨機事件．假設隨機試驗的樣本空間是開單位圓盤，樣本點遵循無差別原則，按照幾何概型的一般解法，隨機事件E的概率(E)等于該事件所有可能結果所形成區(qū)域E的面積(E)與單位圓的面積(D)之比，即

(E)=(E)/(D)．

一切顯得如此自然，似乎沒什么問題．現(xiàn)在不妨深究一下：相對于樣本空間單位圓盤，其事件域是什么？是開圓盤的一切子集還是部分子集？哪部分子集？教師在教學過程中交代清楚了嗎？理論上講，飛鏢落在圓盤的任何位置都是可能的，如果問：“假設E是圓盤內(nèi)坐標為有理數(shù)的點，飛鏢落在E中的概率是多少？”這個問題在數(shù)學上并非沒有意義，因為既然做了等可能性假設，一切皆有可能．可是在這里，E的面積是什么？有定義嗎？甚至可以假設E為圓盤內(nèi)的任意子集，然后問飛鏢落在E中的概率是多少？這時(E)又是什么？這說明經(jīng)典的幾何概型概念是不嚴密的，幾何概型中樣本空間的事件域并不清楚．測度論的誕生是概率論之大幸，如果沒有測度論，概率論的這一致命傷恐怕迄今無法補救，是勒貝格與柯爾莫哥洛夫拯救了概率論．

（2）公理化概率論的誕生．

從幾何概型可以看出，概率的定義依賴于“面積”的定義，所以關鍵是如何定義一般集合的“面積”，所謂一般集合的“面積”即是測度．遺憾的是，在一個具有不可數(shù)個點的空間（例如直線上的某個線段或平面內(nèi)的某個區(qū)域）中無論怎么度量集合，在這個度量下，總會有一些集合是不滿足可加性的，如果沒有可加性，所謂概率就無從談起，因為如前所述，可加性是概率的基本特征．因此，不能指望對樣本空間的所有子集定義測度，而只能對其中部分子集定義測度，也就是那些滿足可加性的集合，這就是可測集的由來．有一個問題是自然的，樣本空間中有多少集合不滿足可加性？很不幸，非常多，與可測集一樣多，不過要搞清楚這個問題需要一點集合論與測度論的專門知識，這里就不贅述了，有興趣者可以參考實變函數(shù)或測度論的相關書籍．

具體到一般的樣本空間，對于給定的樣本空間X，其事件域是什么呢？它是由X中的某些（未必是全部）子集構成的集合F，這個集合需要滿足幾個基本條件：

（1）空集ф與全空間X在F中；

從前面的分析可以看出，要求F中的元素滿足上述3點是自然的，將滿足（1）-（3）的集合稱為由X中子集構成的-域，也把F中的元素稱為可測集，通常把(X, F)稱為可測空間．由此可見，可測空間并不依賴于具體的測度．但一般情況下，如果用到可測集，當然就需要給它一個測度，這個測度應該滿足：

（1）(E)≥0，(ф)=0（非負性）；

換句話說，只要滿足（1）與（2），就說它是可測空間(X, F)上的一個測度，所以測度不是唯一的，對應到同一個F，可以定義多種測度．但如果研究一個測度空間（概率空間）則通常與具體的測度有關，或者說測度空間涉及3個要素：空間（樣本空間）X、-域（事件域）F、測度（概率），把(X, F,)稱為測度空間．

那么概率與測度有何不同？回顧概率的定義，概率不僅需要滿足非負性、可加性，還需要滿足全空間的概率為1，因此如果測度空間(X, F,)除了滿足上面的（1）和（2），還滿足：

（3）(X)=1，則稱為概率測度，簡稱為概率，(X, F,)稱為概率空間．簡而言之，所謂概率測度即歸一化的測度（全空間的測度為1），這就是所謂的公理化概率．

從公理化的概率定義可以看出，先有樣本空間才有事件域，最后才有概率，對于同一個樣本空間與事件域，概率分布可能有多種．相對于具體的隨機試驗，其樣本空間未必唯一，關鍵要看關注隨機試驗結果的何種屬性，這在古典概型情形下已經(jīng)做過闡述．所以在研究概率問題時首先需要確定樣本空間、事件域及概率．在同一個隨機試驗中，如果試驗的結果存在不同的屬性，樣本空間可能有多個，如何確定隨機試驗的樣本空間才是合理的？在沒有特別說明的情況下，樣本空間不應該根據(jù)隨機性假設來確定，而應根據(jù)問題的目標來確定，也就是說根據(jù)所關注隨機試驗結果的屬性來確定樣本空間，當樣本空間確定后，談概率問題才是有意義的．按照目標確定隨機試驗樣本空間的原則，如果在一個隨機試驗中事先給出了隨機假定，那么即使是一種等可能性假設，也未必導出古典概型或幾何概型．由于在中學階段僅限于古典概型與幾何概型，所以不宜將類似貝特朗奇論容易產(chǎn)生歧義的概率問題放到中學從而造成人為的陷阱，甚至產(chǎn)生相互矛盾的結果．教材中飛鏢問題的解答與教輔材料（參見文[2]）中從直角三角形的直角頂點向斜邊隨機引射線問題的解答就是典型的兩種相互矛盾的解答，因為飛鏢也可以看成從擲鏢人手中發(fā)出的射線，這無疑大大增加了學生對概率的理解難度．

現(xiàn)在按公理化概率論重新審視一下幾何概型，不妨假設樣本空間是單位圓盤，相對于這個樣本空間的事件域是什么？顯然不可能是圓盤的所有子集構成的集合，否則無論怎么定義測度，總會有一些子集是不可測的．按照勒貝格的測度論，此時合適的事件域是圓盤中所有勒貝格可測子集全體，記為(D)，測度可以是通常的勒貝格測度，它是面積概念的自然推廣，對應的測度空間就是(D,(D),)，將勒貝格測度歸一化，就得到概率空間了．或者按照幾何概型通常的做法，對任意E∈(D)，E的概率(E)=(E)/(D)．

對于勒貝格測度有興趣但又不想了解太深入的讀者不妨參考克萊因的《古今數(shù)學思想》第三冊第44章．

3 重組概率論課堂教學

數(shù)學教育應該遵循幾個基本原則：（1）適應學生的認知水平；（2）在尊重歷史的基礎上改進教學內(nèi)容；（3）杜絕偽情境．就概率而言，首先要幫助學生解決的一個重要問題是認識隨機現(xiàn)象，進而定義隨機事件．不妨就從擲骰子問題開始．例如可以通過如下一些問題展開．

問題1 如果拋一個骰子（或任何物體），骰子會落向哪個方向？地上還是天花板？

這顯然是一個必然事件，因為萬有引力的作用，骰子一定會落到地上．

問題2 假設骰子是一個正立方體，6個面上分別刻有1、2、3、4、5、6六個數(shù)字，并且骰子的密度是均勻的，如果拋這個骰子，當骰子落到地上時，能確定哪個數(shù)字朝上嗎？能確定是偶數(shù)朝上還是奇數(shù)朝上嗎？

學生回答這個問題不會有任何困難，而且學生憑借生活經(jīng)驗多半也能判斷，出現(xiàn)任何數(shù)字的可能性是相同的．退一步說，如果學生不能發(fā)現(xiàn)出現(xiàn)任何數(shù)字的可能性是相同的這一規(guī)律，教師可以進一步引導學生分析問題中的條件“骰子的密度是均勻的”意味著什么？問題2中最后一個問題無疑在暗示學生，在一個隨機試驗中，隨機事件有兩種類型：基本事件以及由若干基本事件組成的隨機事件，基本事件是特殊的隨機事件．

問題2雖然不那么高雅，但它確實是一個真實有效的問題情境，也與概率的“身世”相吻合．如果覺得這個問題不夠高大上，還可以換一個問題．

問題3 學校為了檢查每個班的體育鍛煉情況，決定從每個班級任意抽調一位同學去參加體育測試，為了反映班級真實情況，不得有選擇性地抽調同學．請問比較合理的抽調方法是什么？

這個問題比問題2稍微困難一點，因為需要學生自己想出“合理”的方案．對于高中生而言，他們有足夠的能力回答這個問題：抓鬮．假設班級有50個人，準備50張小紙片，其中一張紙片上寫著參加，另外49張紙片上寫著不參加，可以設計這樣幾個引導式的問題：

（1）能肯定哪個同學一定抽到參加的紙片嗎？

（2）每個同學抽到參加的可能性是否相同？

由于歷史上出現(xiàn)得最早的概率問題正是古典概型，所以沒有必要急于讓學生了解一般的隨機事件，就針對古典概型來討論就可以了．

通過上述幾個問題的討論，學生對必然事件、隨機事件已經(jīng)有了初步認識，在此基礎上不妨給出古典概型的嚴格定義．同時，應該給出基本事件、樣本空間及隨機事件的數(shù)學定義．什么叫基本事件？不能簡單地用隨機試驗所有可能的“基本結果”來定義基本事件，因為并沒有給出基本結果的定義．為了說清楚基本事件，不妨引入互斥事件的概念，這在理解上并無任何困難：“兩個不可能同時發(fā)生的隨機事件稱為互斥事件．”當然，不作這種調整也不妨礙對基本事件與隨機事件的理解．按照標準的定義，隨機試驗所有可能的結果組成的集合稱為樣本空間，每一個可能的結果都稱為基本事件或樣本點．教材中正是因為將“在一定條件下，可能發(fā)生也可能不發(fā)生的結果稱為隨機事件”導致后面對基本事件的定義帶來了含混．基本事件應該滿足兩個基本條件：（1）任何兩個基本事件是互斥的；（2）任何隨機事件都可以表示成若干基本事件的和（即若干基本事件組成的集合）．基本事件A與B互斥即指若A發(fā)生則B不可能發(fā)生，反之亦然．可以通過擲骰子中任何兩個數(shù)字不可能同時出現(xiàn)來說明這個問題，或者通過同學抓鬮時不可能既抓到參加的紙片又抓到不參加的紙片說明．

初識樣本空間、基本事件以及隨機事件之后，需要對基本事件與隨機事件加以辨析，也就是什么叫任何隨機事件都可以表示成若干基本事件的和？仍然可以通過擲骰子來說明，例如可以進一步設計這樣的問題．

問題4 隨機擲一枚骰子，如果問出現(xiàn)偶數(shù)的概率是多少，這時所指的隨機事件是什么？如何計算該隨機事件的概率？

有了以上的討論，可以由學生自己提供一些隨機現(xiàn)象的例子，善于思考的學生也許不僅僅想到擲硬幣，樣品抽檢之類的隨機現(xiàn)象，甚至可能想到天氣、地震之類的現(xiàn)象也是隨機的，但這些隨機現(xiàn)象就不是上述方法可以處理的了．

清楚了古典概型及其概率的計算，接下來的單元是幾何概型，這是教學中的難點，教材中幾何概型的定義是不嚴格的，給出一般的幾何概型定義并不會增加學生對幾何概型理解的困難，幾何概型的難點在計算而不是概念，所以教材應該給出嚴格的數(shù)學定義．課堂上可以通過類似下面的問題展開．

問題5 士兵在練習實彈射擊時，能肯定子彈會射中靶子上的哪一點嗎？

這與擲飛鏢本質上是一個問題，而且現(xiàn)實的扔飛鏢與實彈射擊都不是幾何概型，不過，不妨假設擲鏢人或士兵是初學咋練，鏢或子彈射中靶子的任何一點是等可能的，這個問題也為后面引入非等可能性概率問題埋下伏筆．通過這個問題的討論，可以引出樣本空間無限的概率問題．即

定義 如果一個隨機試驗所有可能的結果有無限多個，且每一種結果都是等可能的，則稱這樣的概率模型為幾何概型．

在此基礎上可以引導學生找出一些幾何概型的例子，包括一維、二維甚至三維情形下的幾何概型．在學生對幾何概型有了比較多的了解后，有必要向學生說明幾何概型未必如想象的那樣一定是空間中某些區(qū)域構成的樣本空間，但不宜太詳細，因為以學生的知識積累尚不足以理解一般的無窮集以及測度，教師如果清楚，可以做科普式的介紹，不清楚則一帶而過．

無論是教材還是在課堂都不宜將類似教輔材料（參見文[2]）中從直角三角形直角頂點隨機引射線等問題放在中學階段學習，這會引起學生對幾何概型的困惑，只有當學生在概率方面有了相當?shù)乃仞B(yǎng)后才適合研究那類問題．具體地說，中學階段的概率問題最好都是樣本空間比較容易明確的那些問題，設置一些類似貝特朗問題的陷阱并不能給學生理解概率帶來任何實質性幫助，即使作為課外參考，也不應該與教材在邏輯上相悖．例如教材中擲飛鏢等問題也可以理解成從擲鏢人手中隨機拋出的射線，按照這樣的邏輯來理解，很多概率問題都會帶來歧義甚至是不可解的．例如隨機拋一粒沙子的問題就不是中學生能解決的，如果拋沙子的角度不定，問題就不可解．解決這個問題的比較好的辦法是命題人在擬定題目時將目標（隨機事件的概率）與等可能性假設相一致．正如擲飛鏢問題中，因為目標關注的是飛鏢的著靶點，所以針對靶子上的點做等可能性假設比較合適，否則擲鏢人站在不同的位置，就會得到不同的概率問題．在學習了一般的概型之后再適當研究這類問題并無不可，只是這些問題不適合中學生．

概率必修教材在幾何概型之后便是互斥事件，如果不講選修內(nèi)容，概率到互斥事件就算結束了．僅就必修教材的編寫看，概念的定義稍顯粗糙，邏輯也不夠嚴謹．可以考慮首先介紹一般的隨機試驗，然后定義隨機事件與互斥事件，在此基礎上定義基本事件與樣本空間，再介紹古典概型與幾何概型．按照這樣的體系編寫既符合概率論發(fā)展的歷史脈絡，概念也不失嚴謹．

說到選修2-3中的概率章節(jié)，教學內(nèi)容可能需要做比較大的改進．

學生對隨機現(xiàn)象與隨機事件已經(jīng)有所了解，沒有必要每章每節(jié)開頭必要以不同的“生活化”例子開頭，好的例子可以反復使用，從不同的角度進行研究．為了引入隨機變量，首先需要引導學生思考，如何利用數(shù)學語言表示現(xiàn)實中的隨機現(xiàn)象？或者說如何用符號化的語言表示隨機現(xiàn)象或隨機事件？不妨還是從擲骰子開始．

問題6 首先回憶一下在利用數(shù)學方法研究確定性實際問題時，首先要做的一件事是什么？擲骰子試驗的樣本空間是什么？如何用合適的方法表示擲骰子試驗？

問題7 拋硬幣試驗的樣本空間是什么？如何用數(shù)學方法表示這個試驗？

問題8 如果知道了隨機試驗的樣本空間，如何用數(shù)學方法把這個試驗表示出來？

通過上述3個問題的分析，不難逐步引入隨機變量的概念，完全沒有必要通過左一個右一個的例子做直觀的闡述，可以給出隨機變量的嚴格數(shù)學定義，直觀解釋可以幫助學生理解概念，但不能代替概念的嚴格定義．

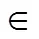
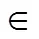
問題10 在擲骰子試驗中，樣本空間為{1, 2, 3, 4, 5, 6}，如何用隨機變量表示出現(xiàn)偶數(shù)或奇數(shù)的隨機事件？

限于篇幅，對于更一般的隨機試驗將另文討論．

[1] M·克萊因．古今數(shù)學思想（第三冊）[M]．上海：上海科學技術出版社，2014：201-210．

[2] 高中新課程學習指導編寫組．成才之路（數(shù)學必修3）[M]．北京：中國和平出版社，2012：64-65．

On the Teaching of Probability in Middle School from the Perspective of Historical Development

ZHANG Shu-qing1, CAO Guang-fu2, LUO Li-ling2

(1. Zhixin High Middle School, Guangdong Guangzhou 510095, China;2. Faculty of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China)

In the context of historical development, this paper made a brief and concise exposition of the development of the theory of probability from the probability of classical probability to statistics and then to the probability theory of axiomatic. It was convenient for teachers to have a preliminary understanding of the basic history of probability theory. At the same time, through the creation of a series of problem situations, it put forward some practical suggestions for the teaching of random events, sample space, classical probability and geometric probability model in the middle school class. The article thought, probability teaching should follow a few basic principles: 1, adapt to the student’s cognition level; 2. Improving teaching content based on respect for history; 3. No false situations. It also argued that the definition of concepts should be accurate and the logical relationship between different concepts (basic events, sample spaces, random events) should be clear. In high school, it was not appropriate to design some trap of Bertrand problem, which, apart from increasing the difficulty of students’ understanding of geometrical models, did not help students’ learning probabilities.

random events; sample space; classical probability; geometric probability model

[責任編校：周學智]

2018–04–19

國家“萬人計劃”領軍人才、廣東省“特支計劃”、廣州市教育名家工作室聯(lián)合資助

張蜀青（1973—），女，廣東廣州人，高級教師，博士生，主要從事中學一線教學與數(shù)學教育研究．

G420

A

1004–9894（2018）04–0035–06

張蜀青，曹廣福，羅荔齡．從歷史發(fā)展的視角看中學概率教學[J]．數(shù)學教育學報，2018，27（4）：35-40．