一種基于à Trous算法的水下圖像增強算法

黃允滸，韓燕，吐爾洪江·阿布都克力木

（1.新疆師范大學數學科學學院，新疆 烏魯木齊 830017；2.新疆和靜縣第九小學新疆 和靜841304）

由于水體本身性質，光學特性和懸浮體等的存在，造成水下圖像對比度差，噪聲大等缺陷。然而這些缺陷影響著水下圖像的后期處理，如圖像分割、特征提取以及目標識別等，這也使得水下圖像增強也越來越受到重視[1]。

現有的水下圖像增強的方法主要有變換域增強，空間域增強[2-3]。其中基于變換域增強方法主要基于多尺度分析，如傅里葉變換，小波變換，二進小波變換[4]，Contourlet變換[5]，非下采樣Contourlet（Nonsubsampled Contourlet Transform ，NSCT）變換[6-7]等，而傅里葉變換在變換時會造成信號細節損失；小波變換只能描述點奇異性，往往使圖像邊緣變得粗糙；二進小波變換在分解和重構時未進行采樣操作，因此圖像（信號）在二進小波域表達是及其冗余的，平移不變性在圖像去噪，增強等眾多領域的應用中有著重要的意義，它保證了圖像原有的重要信息的位置在二進小波域中不會有很大的偏移，不會使圖像在預處理時而平滑掉某些重要信息，部分系數擾動不會引起重構圖像的嚴重失真，可以有效避免由于非線性變換引起的視覺形變；NSCT克服了Contourlet變換由于缺少平移不變性，有效降低了信號在重構時引起的偽吉布斯振蕩問題，且在保留圖像細節信息同時能達到良好去噪效果，但其缺點是運算量大的缺點，相比之下，二進小波變換數學結構較為簡單，運算復雜度更低，能提高算法的時間效率，適用于圖像增強，去噪和融合領域。

基于空間域增強方法是直接對圖像的灰度值進行處理。利用本文方法對大量水下圖像進行實驗分析，為避免主觀性和經驗主義帶來的局限性，根據主觀效果及清晰度，信噪比（PSNR）和絕對均值差（MAE）作為對水下圖像的客觀評價方式，并與目前圖像處理中最具代表性的多尺度增強方法對比，實驗結果表明，本文提出的方法在主觀上能有效改善水下圖像的視覺效果，客觀指標中，圖像的清晰度，信噪比都有大幅提升。

1 算法原理與分析

二進小波變換是對連續小波變換的頻域抽樣。因此，它既彌補了連續小波變換在處理圖像時所存在的不足，又繼承了其平移不變性表示的優點，致使完備的子帶系數適用于圖像增強。由于該變換不需要嚴格的子采樣，因此可以保留圖像的細節信息，從而避免偽像和空間變形。二進小波平移不變性和各尺度上系數相關性，不會使圖像在預處理時而平滑掉某些重要信息，部分系數擾動不會引起重構圖像的嚴重失真，有效改善圖增強過程中噪聲放大，對比度差的問題。為了提高該算法的時間效率，本文采用二進小波變換快速算法－à Trous算法[8-9]。該算法是在Mallat提出的二進小波變換基礎上的改進，其基本思想并沒有發生改變，由于能描述信號的局部特征，在一定程度上克服了“Mallat小波變換單純增強細節信息，存在噪聲放大等問題”。其基本思想是把信號或圖像的高低頻信息分離，將其分解為不同頻率通道上的近似信號和小波平面。

通過利用二進小波變換域內數據表達很大冗余性，便于對每個尺度下的細節和概貌進行頻譜分析，可以有效避免由于非線性變換在邊緣不連續所引起的偽吉布斯現象，在相同誤判概率下，二進小波變換可改變圖像重建效果，可以降低圖像在重建過程中產生的人工噪聲。相比于其他去噪算法，二進小波變換的圖像去噪方法對噪聲水平有很強的穩定性[9]。因此，現將一維à Trous算法進行推廣并將其應用于圖像的變換和反變換過程中，本文利用二進小波來處理水下圖像，以求獲得更高質量圖像。

在城市規劃中，不僅要考慮城市布局問題，還要考慮城市規模。首先應在災害評估的基礎上，做好防災規劃，然后進行城市發展的其他規劃編制。

文中選取r=2,m=1時具有線性相位，緊支撐，高階消失矩的B-樣條二進小波濾波器作為初始濾波器作為初始濾波器。基于二進提升方案，通過調整提升參數的形式，能夠構造出具有更高階消失矩的提升二進小波濾波器[8-9]。初始濾波器尺度函數和小波以及提升二進小波對應的尺度函數和小波分別如圖1和圖2所示。

2 算法實現

2.1 二進小波域低頻子帶系數處理

噪聲具有很大隨機性，在二進小波域中不具有固定的幾何結構特征，經二進小波變換產生的低頻子帶中幾乎不含噪聲信息，它就像是源圖像的縮略圖[10]，包含了原始輸入圖像邊緣亮度等關鍵信息，它對原始圖像最大影響是對比度，為了有效改善圖像亮度分布均勻性，用線性拉伸方式提高圖像整體對比度，增加圖像的層次感。采用如下線性映射方式，將低頻子帶系數映射到[0，255]區間內。

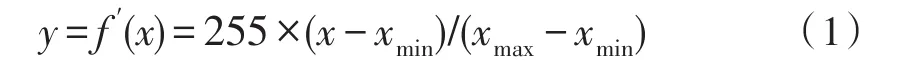
其次利用式（1）將處理后的系數映射到[xmin,xmax]區間內，式中xmin與xmax分別為低頻系數中的最小值與最大值，f′(i,j)為線性變換的結果。

2.2 二進小波域高頻子帶抑噪處理

圖像經二進小波變換后，高頻子帶系數包含圖像中大量的細節信息和噪聲，對高頻子帶系數調整目的是去除噪聲，增強弱邊緣和細節信息[11]。本文選取如下連續非線性函數H(x)來調整高頻子帶系數

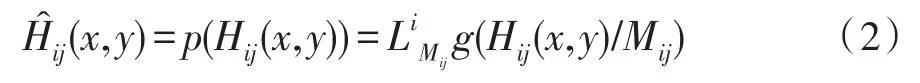
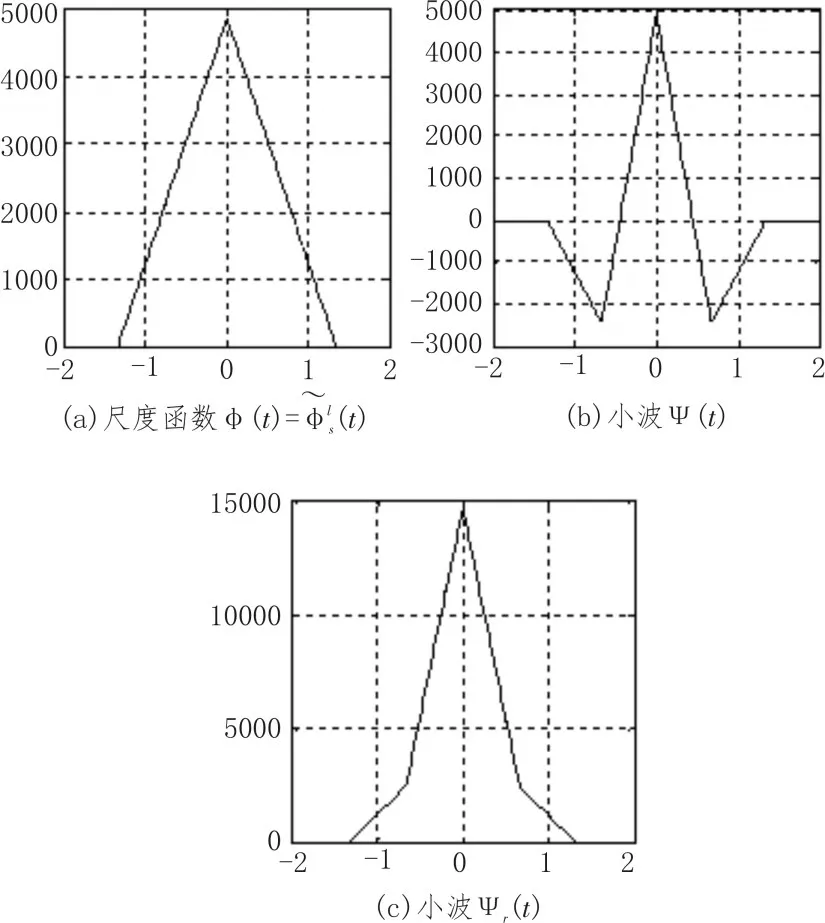
圖1 尺度函數與小波(?(t)='s(t),ψ(t),ψr(t))的圖像

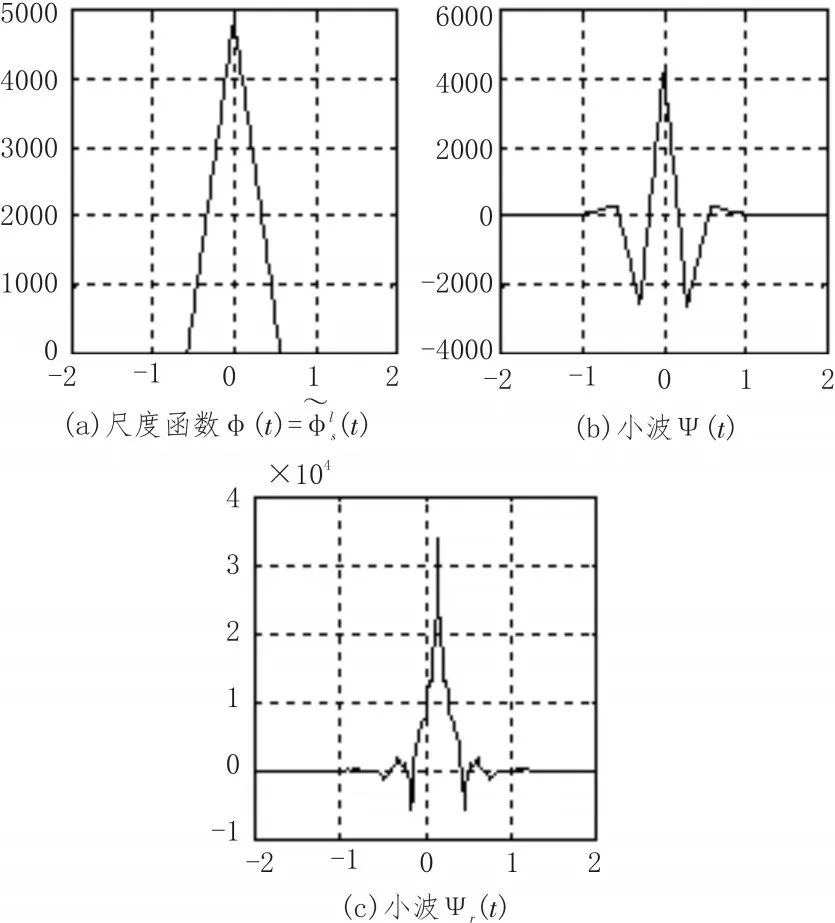
圖2 提升二進小波尺度函數和小波

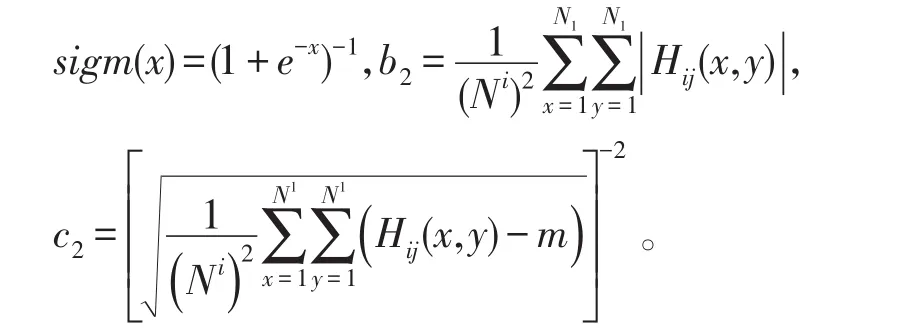
其中Ni為i尺度子帶大小，Li的值是與尺度相關的最重要參數，b2為控制著非線性增強函數的形狀參數，控制著曲線斜率的變化。為保證Hij中的大部分系數能得到增強，其增益倍數必須滿足大于1，因此參數b2由下式自適應確定，即：

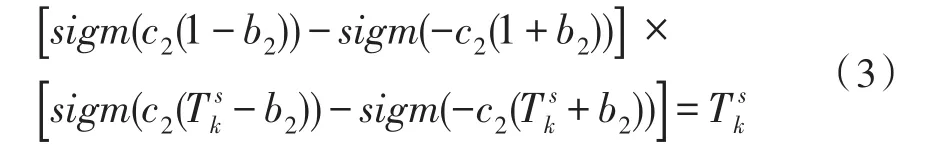
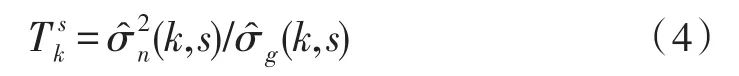
改進的閾值公式可表示為：

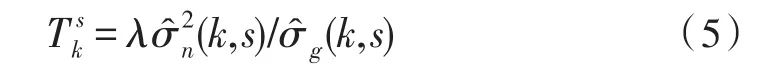
λ為第k尺度，s子帶內閾值的改正因子，可以表示為，其中和分別表示為二進小波域內第k尺度第s子帶系數絕對值的平均值和第k尺度的所有子帶系數絕對值的平均值[12-13]。整體系數較小的子帶通過改正因子使得閾值因子也相對較小，能夠保留更多的系數，而對于較大的子帶系數通過增大閾值以抑制更多的噪聲，減少重構圖像的嚴重失真，提高圖像的重構質量。

與分別為噪聲方差和信號方差，取值分別由下式得到：

根據上述分析，高頻子帶系數可按下式進行調整

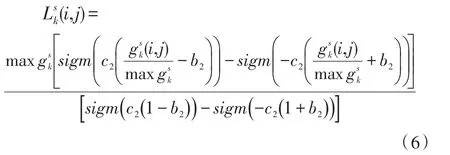
3 改進的模糊對比度

經過二進小波反變換得到水下重構圖像，基本上已經除去了噪聲的影響，但細節和對比度有待進一步提升。但還是存在對比度較低，邊緣不夠清晰。因此可以直接利用模糊對比度增強來處理二進小波反變換后的圖像，這樣既能提高水下圖像整體對比度又能避免噪聲放大。

1981年，Pal和King等人首次在將模糊理論應用于圖像增強中[14]，并取得良好的效果，究其原因在于：圖像的不確定性是由于圖像模糊性導致的。因此，可以把圖像的灰度認為是一模糊概念而采取模糊處理的技術[15-16]。一幅大小為M×N，具有[0,L-1]個灰度級的水下圖像可以作為一個模糊點集看待：

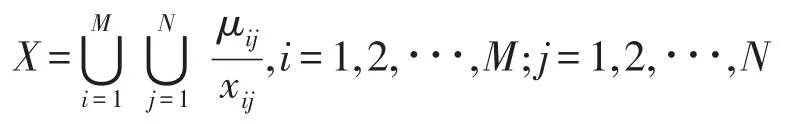
xij表示圖像在(i,j)處的灰度值，μi,j/xi,j表示xij相對于某種特征μij的隸屬度。文獻[15]給出了歸一化模糊對比度概念：

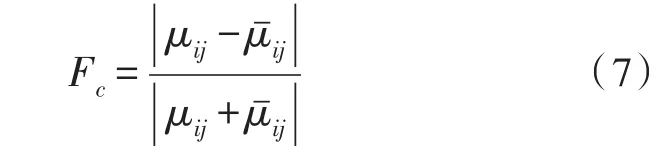
其中為3×3窗口的去心領域的均值，即

本文選用線性隸屬度函數將圖像由二進小波域變換到模糊特征平面：

L表示水下圖像的灰度級，模糊對比度改進公式如式所示

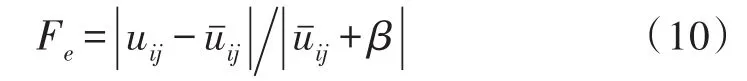
式中β為微調因子，文中取β=0.4，為適應不同類型圖像的處理，一般β取值為[0.3,0.5]，這樣做使得Fe有了更明確的定義：即像素點xij隸屬度與其領域均值隸屬度之差的絕對值相對于像素點灰度均值的隸屬度的比值。

對Fe進行非線性變換Fe′=ψ(Fe)，ψ(Fc)為一凸函數，且使得ψ(0)=0,ψ(1)=1，ψ(x)≥0.本文選取增強函數定義如下：

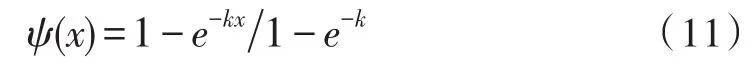
改進的隸屬度函為：

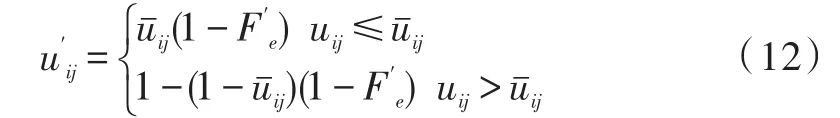
將隸屬度函數從模糊域轉回二進小波域

4 本文算法實現流程

圖像增強算法按如下步驟進行：

1）對輸入水下圖像進行直方圖均衡化，以提高圖像整體對比度；

2）取r=2,m=1的B-樣條二進小波濾波器作為二進小波分解與重構基，按文獻[8]中的（1）式～（4）式對直方圖均衡化的水下圖像進行二進小波變換，得到一個低頻子帶系數和多個高頻子帶系數；

3）通過（1）式對低頻子帶系數進行線性拉伸提高圖像整體對比度；按照（2）式～（6）式對不同子帶的高頻系數進行Bayes閾值估計和非線性增益調整，得到對比度增強和噪聲抑制的圖像；

4）對低頻子帶系數和高頻子帶系數進行二進小波反變換，得到的圖像按照（9）式～（12）式進行模糊對比度增強。

5）通過（13）式將圖像從模糊域變換回二進小波域，得到增強后的水下圖像。

5 實驗結果與分析

為了檢驗本文算法對于水下圖像的增強效果，選取紋理信息較為豐富的圖像，大小分別為512像素×512像素的淡水魚圖像，并截取其中大小為256像素×256像素的潛水員水下作業圖像的一部分作為測試樣本，實驗中采用的濾波器為T.Abdukirim構造的二進小波濾波器[8-9]，本文選取具有緊支撐，對稱性和高階消失矩特點的B-樣條二進小波濾波器(r=2,m=1)作為二進小波分解和重構的初始基。同時將本文方法與文獻[6，11，18]的方法進行比較，并分別從客觀和主觀上分析提出的算法對性能進行評估。

因為仿真實驗過程中，不同濾波器的選取，參數的選取和分解層數的確定，都直接影響到圖像的視覺效果，分解層數不宜過多，否則圖像會由于失去較多高頻成分而模糊，所以文章對基于非下采樣Contourlet變換[6]（NSCT）分解均為3層分解。通過主觀和客觀方式來比較各種算法的增強效果，主觀評價主要通過視覺方式對比各種算法增強效果，選取清晰度、均值、絕對均值差（MAE）作為對水下圖像的客觀評價方式。清晰度也稱平均梯度，它反映圖像的紋理特征，其值越大說明圖像越清晰；均值反映圖像的平均亮度，亮度適中（一般在128附近），表明視覺效果良好[21]；信噪比能客觀反映出各算法的抗噪性能；絕對均值差反映圖像對比度大小，其值越小表示圖像的整體對比度越好。所有方法的實現是基于Matlab2010a實驗平臺，硬件設備為 Intel（R）Core（TM）i5 CPU2@2GHz/2GB內存，PC機。參數設置如下：基于NSCT變換中，選用非下采樣塔形‘maxflat’濾波器進行尺度分解，非下采樣方向濾波器組選用‘dmaxflat7’，所對應的方向數目分別為 8，16，16。多尺度Retinex算法選取3個尺度，尺度N取3，標準差σk分別取值為25，73，87，權重都為1/3。算法增強效果如圖3，圖4所示。

圖3 淡水魚圖像增強效果比較

從圖3和圖4分別為淡水魚圖像，潛水員水下作業圖像采用不同增強方法進行增強處理的效果圖。由增強結果可以看出，原水下圖像整體偏暗，對比度差和細節模糊。增強結果可以發現，文獻[6]，文獻[11]和文獻[18]方法均不同程度提升了圖像的對比度，圖像細節、紋理信息進一步得到改善。其中文獻[11]方法對部分細節描述不足，圖像的紋理細節和總體對比度沒有明顯提高；文獻[6]方法提升了圖像的可讀性、層次感更好，但并未顯著提高圖像對比度；文獻[18]增強方法處理后，細節和紋理信息描述不足，出現過度增強，使原本暗的地方更暗，亮的地方更亮，如潛水員水下作業圖像的細節沒有明顯改善。本文方法獲得了最佳的視覺效果，較好地呈現淡水魚，潛水員水下作業圖像的紋理和細節信息，有效突出水下圖像的陰影和背景部分，在有效提升對比度同時，能夠對淡水魚圖像，潛水員水下作業圖像的魚群和海底生物進行清晰的描述。

表1 對應圖3的客觀評價標準

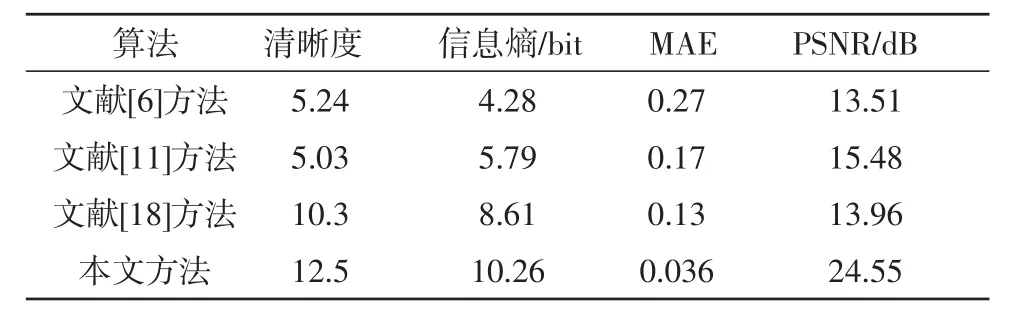
表2 對應圖4的客觀評價標準

圖4 潛水員水下作業圖像增強效果比較

從視覺效果來分析實驗有一定局限性，帶有主觀性和經驗主義，然而在實際應用中水下圖像包含著豐富的空間高頻分量和地貌地形等細節信息。因此表1，表2給出了圖3和圖4的客觀評價標準，表1，表2的數據結果客觀上說明了各個方法的差別，文獻[18]方法增強后的水下圖像的清晰度和灰度平均值與本文方法接近，但PSNR明顯低于本文方法。文章提出的增強方法在絕對均值差（MAE）都低于其它算法，說明本文方法比其他方法對比度更高。

綜上可知本文的算法由于其他增強算法，取決于以下3個方面，一方面充分利用二進小波平移不變性和各尺度上系數相關性，選擇具有緊支撐，對稱性和高階消失矩特點的B-樣條二進小波濾波器作為二進小波變變換的分解和重構基，不會使圖像在預處理時而平滑掉某些重要信息，部分系數擾動不會引起重構圖像的嚴重失真，且數據表達有很大冗余性，便于對每個尺度下的細節和概貌進行頻譜分析，有效避免了由于非線性變換在邊緣不連續所引起的偽吉布斯現象，其次對高頻子帶信息進行Bayes閾值估計和非線性增益調整，有效增強水下圖像對比度和改善圖增強過程中噪聲放大，對比度差的問題；另一方面對重構的子帶系數通過模糊對比度處理增強水下圖像邊緣細節，提高圖像對比度的同時，更好緩解了水下圖像邊緣處引入噪聲與水下圖像模糊間的矛盾。

6 結束語

提出一種基于à Trous算法的水下圖像模糊集增強算法。該方法利用二進小波變換，模糊對比度增強的特點，增強圖像邊緣細節，提高圖像對比度的同時，更好緩解了圖像邊緣處引入噪聲與圖像模糊間的矛盾，利用改進的帶可調因子的Bayes閾值去噪法對高頻子帶系數抑噪處理，最大程度濾除由于圖像本身的噪聲和變化過程可能產生的噪聲，并通過模糊對比度增強進一步提高圖像全局對比度，可以在圖像失真和噪聲放大中尋找到平衡點。與目前圖像處理中最具代表性的多尺度增強方法:二進小波變換，NSCT變換等相比。實驗結果表明，本文方法對水下圖像增強在主觀上能使圖像紋理細節信息更突出，對比度明顯提高，視覺效果更好，客觀上圖像的清晰度和信噪比都有很大的提升。