船用離心泵低頻振動特性分析

，，，

(武漢理工大學 a.能源與動力工程學院；b.高性能船舶技術教育部重點實驗室；c.船舶動力系統運用技術交通行業重點實驗室,武漢 430063)

離心泵在正常工作時會引起艦船殼體的低頻振動，進而會向流場周圍輻射噪聲，對艦船的聲隱身性能極為不利。目前已有的離心泵振動相關的研究主要針對泵體的振動特性[1-3]，或者針對內部非定常流動誘發的流體激勵特性[4-8]，關于離心泵不同工況下的機腳振動特性研究未見報道。由于離心泵內部流場受到結構影響而產生的交變壓力脈動是產生振動的主要原因之一，而流固耦合方法適用于解決離心泵的結構與內部非定常流場相互影響的問題[9-12]，因此考慮建立流體域、離心泵、轉矩轉速傳感器、三相異步電動機以及機座的有限元模型，采用流固耦合方法對離心泵在不同工況下0～400 Hz內的機腳振動特性進行分析。

1 計算模型

1.1 模型參數

以IS100-65-315單級單吸臥式離心泵為研究對象，其設計參數見表1。

1.2 三維建模和網格劃分

利用Pro/E分別建立離心泵流道計算域、整個泵體(包括蝸殼、葉輪、支架)、轉矩轉速傳感

表1 離心泵設計參數

器、三相異步電動機以及機座的三維模型。為保證計算的可行性，提高運算速度和運算精度，未考慮泵體上的小孔、凸臺和倒角。此外，在保證轉矩轉速傳感器和三相異步電動機質量不變的情況下，將其簡化成實心圓柱體。機座材料是結構鋼，其他結構材料是鑄鐵，材料的屬性見表2。

表2 材料特性參數

利用Workbench的網格自動劃分功能實現結構區域網格的生成，網格尺寸d應小于薄板振動波長λ的1/6，即d≤λ/6。經計算，d≤64 mm，因此單元尺寸取為4 mm，滿足要求，網格數量為813 681。利用ICEM CFD軟件對流體區域進行網格劃分，由于流體域的形狀比較復雜，因此，采用非結構化四面體網格進行劃分。網格尺寸和結構體網格尺寸相同。由于蝸殼隔舌的曲率變化較大，生成的網格質量較差，因此，對該部分進行局部加密，最終流體域的網格總數為2 395 477。計算域網格見圖1。

圖1 計算域網格

2 數值計算理論

2.1 流體域計算控制方程

對離心泵內部流場采用RANS法進行計算，選用標準k-ε湍流模型，其控制方程組如下[13]。

1)連續方程。

(1)

2)動量方程。

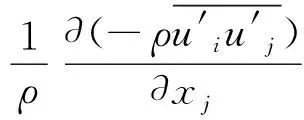
(2)

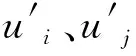
湍動能和湍動能耗散方程分別為

(3)

(4)

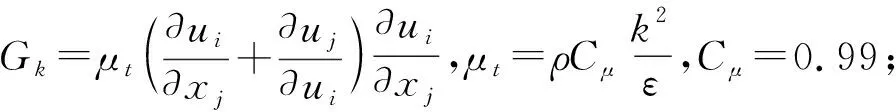
2.2 結構域計算控制方程

離心泵在運行過程中，系統結構每一時刻都承受著流體運動產生的壓力，從而引起結構的振動，運用有限元法進行瞬態動力學分析，控制方程為[14]

Mx″+Cx′+Kx=F(t)

(5)

式中：M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；x、x′、x″分別為位移矢量、速度矢量、加速度矢量；F(t)為力矢量。

2.3 數值計算方法

用CFX對流體計算區域進行流場的非定常計算，用Workbench 對結構區域進行瞬態動力學分析。取定常計算結果為其初始條件。在進行流固耦合計算時，分別將結構域的蝸殼、葉片、葉輪前蓋板、葉輪后蓋板與流體接觸的面設置為流固耦合面，對控制方程采用有限體積法進行離散，湍流模型選用標準k-ε模型。進出口條件分別采用壓力進口、均速出口，采用標準壁面函數對近壁區進行處理。對流場每隔9°計算一個時間點，即每個計算時間步長為10-3s，葉輪旋轉3個周期，一共120個時間步，對3個周期內的流場和結構場的響應進行計算。采用Second Order Backward Euler格式對流場進行瞬時求解，殘差收斂目標設置為10-5。流固耦合計算數據傳遞過程的松弛因子設置為默認值0.75，收斂標準設置為10-3。通過設置不同出口速度對0.60Q～1.40Q5種工況的流動進行模擬。

3 模擬結果

3.1 離心泵外特性和振動特性試驗驗證

搭建離心泵試驗臺架，進行清水試驗。對離心泵5種工況的揚程和效率進行測量，同時在每個機腳上布置兩個測點，對其設計工況下的機腳振動加速度進行測量，測點位置見圖2。將數值模擬結果與試驗結果進行對比，從而對流固耦合計算結果的可靠性和模型的正確性進行驗證。

提取離心泵流固耦合最后一個周期內計算得到的瞬時進、出口壓力和轉矩，每隔4個時間步長提取1次，并對數據按照式(5)、(6)進行處理，得到各個工況下的揚程與效率，由此繪制出Q-H、Q-η外特性曲線，并與試驗所得到的外特性曲線進行對比，見圖3。泵揚程和效率的計算式如下。

(6)

(7)

圖2 測點布置示意

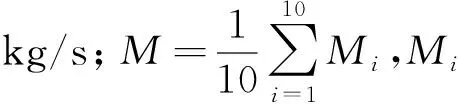
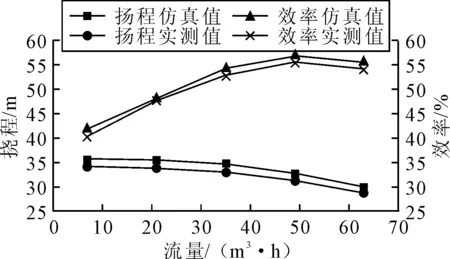
圖3 離心泵外特性

由圖3可見，流固耦合計算得到的離心泵的外特性曲線與試驗得到的趨勢基本一致，即揚程隨著流量的增大而減小，效率隨著流量的增大先增大后減小，且在流量為1.20Q時達到最大。該離心泵比轉數為46，屬于低比轉數泵，揚程、效率曲線也符合低比轉數泵的變化趨勢。在設計工況附近，揚程的仿真值與試驗值誤差為5%，其余工況誤差均在4%左右，不超過5%。對于效率曲線，在小流量工況時誤差最大，為3.20%，其余工況誤差均在3%以內。

分別提取離心泵設計工況下1號、3號、6號測點振動加速度的仿真值和試驗值，對6個頻率點處的振動加速度級進行對比，見表3。

由表3可見，設計工況下機腳的振動加速度級仿真值和實驗值相差不大，所有頻率點處加速度級差值的平均值為1.97 dB，其中只有3個頻率點處的差值超過了3 dB，其余頻率點處的平均值為1.33 dB。因此，仿真計算結果基本反映了離心泵機腳在設計工況下的振動特性。從總體來看，流固耦合計算的結果比較可靠，所建立的模型也滿足仿真的要求。

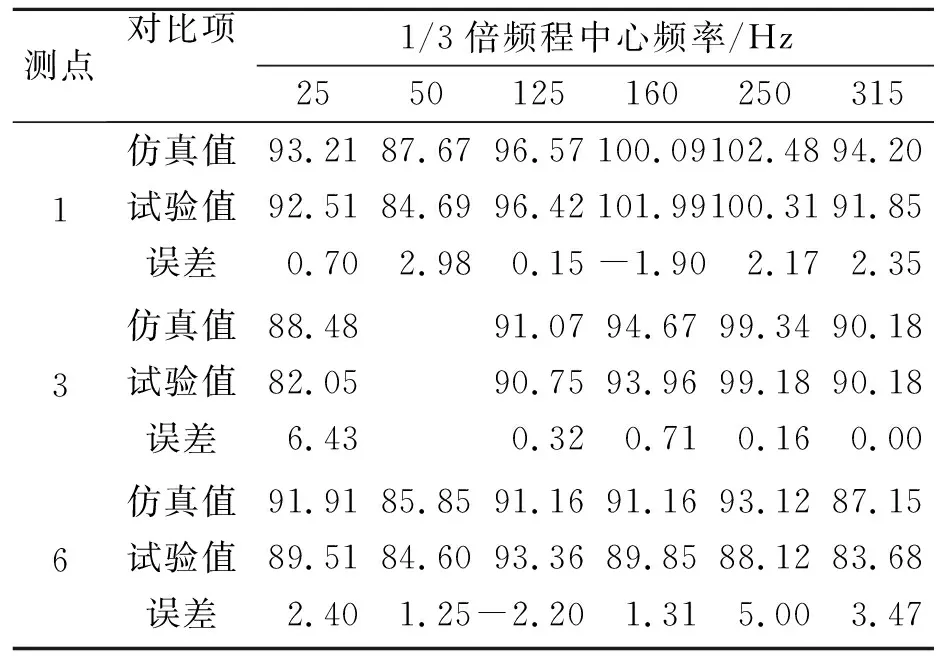
表3 離心泵機腳振動加速度級對比 dB

3.2 離心泵在設計工況下的流場分布

分別對第3個計算周期內T/4、T/2、3T/4、T時刻的流場進行比較，見圖4。

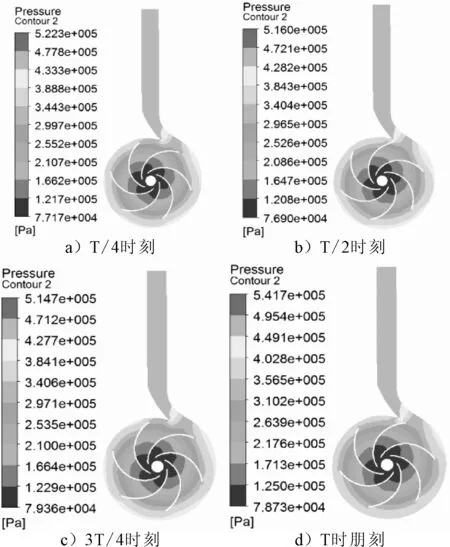
圖4 不同時刻的流場壓力云圖

由圖4可見，在這4個時刻，最小壓力均出現在葉輪的中心位置，為7.87×104Pa；最大壓力均出現在出口延長段，為5.42×105Pa，約為最小壓力的6.59倍。葉輪區域的流場壓力自葉輪中心沿著半徑方向逐漸增大，直到葉梢達到最大，這是因為葉輪在旋轉時對流體產生離心力，并且沿著半徑逐漸增大，最終在葉梢達到最大。蝸殼區域的流場壓力在蝸舌處最小，并且沿著流道逐漸增大，直到蝸殼出口處達到最大，這是因為蝸殼截面面積沿著流道逐漸變大，有擴壓的作用。

3.3 離心泵在設計工況下的振動特性

對離心泵在設計工況下的流動進行仿真，得到的加速度云圖見圖5。

由圖5可見，離心泵出口處的振動加速度比機腳處的大，這是因為機腳處施加了約束，出口端沒有施加約束，是自由狀態。

提取離心泵設計工況下機腳處的加速度仿真值，分別對6個測點最后2個葉輪旋轉周期內的數據進行傅里葉變換，得到0～400 Hz范圍內的頻譜，見圖6。

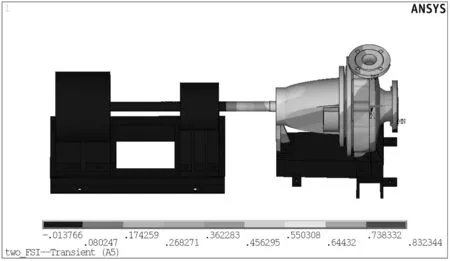
圖5 離心泵振動加速度云圖

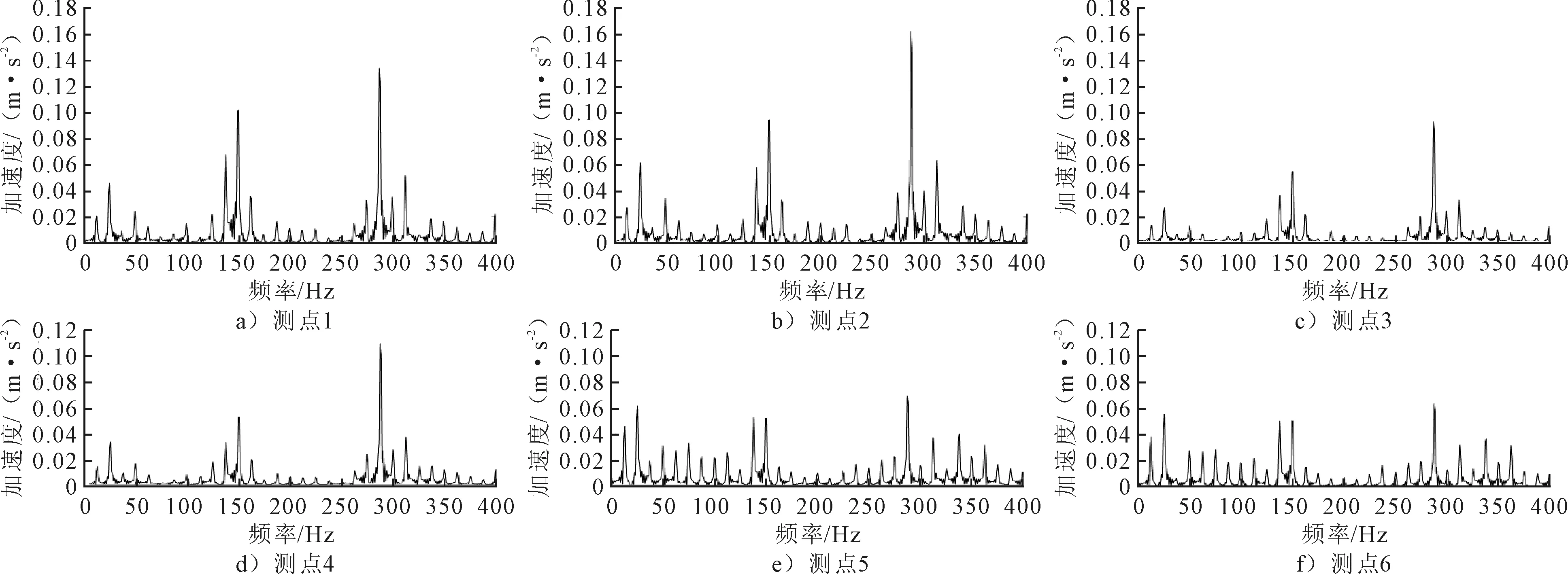
圖6 離心泵機腳振動加速度頻譜

由圖6可見，6個測點均在25.39 Hz出現第1個峰值，離心泵的轉速為1 450 r/min，轉頻為24.17 Hz，說明離心泵在其轉頻處振動比較強烈。此外，在150.40、287.10 Hz也出現了很明顯的峰值。該離心泵有6個葉片，其葉頻為145.02 Hz，說明離心泵在葉頻和葉頻2倍頻處也會產生強烈振動，其中1、2、3、4測點在150.40、287.10 Hz處的峰值均比24.17 Hz處高，5、6測點在此頻率下的峰值與24.17 Hz處的相差很小，這是由于1、2、3、4測點位于蝸殼一側，而離心泵在正常工作時旋轉的流體會對蝸殼產生周期流體激勵力，導致蝸殼處的機腳在葉頻和葉頻的倍頻處產生比較強烈的振動；5、6測點位于遠離蝸殼的一側，沒有受到周期流體激勵力的直接作用，因此在葉頻和葉頻2倍頻處產生的振動比較小。

從圖6還可以看出，測點1與測點2、測點3與測點4、測點5與測點6的頻譜圖均比較相似，為方便比較，分別對其中8個頻率點處的加速度級進行對比，見表4。

由表4可見，相同機腳不同測點處相同頻率下的振動加速度級相差很小，所有頻率點處差值的平均值小于1.30 dB，其中只有4個頻率點處的差值超過了2 dB，最大差值為3.28 dB，其余頻率點處的差值皆小于2 dB，其中75%的頻率點處的差值小于1.50 dB。因此判斷每個機腳可以只提取1個節點的加速度進行振動特性分析；同時，在搭建離心泵機腳振動試驗臺架時，只需在每個機腳處布置1個測點就可滿足要求。

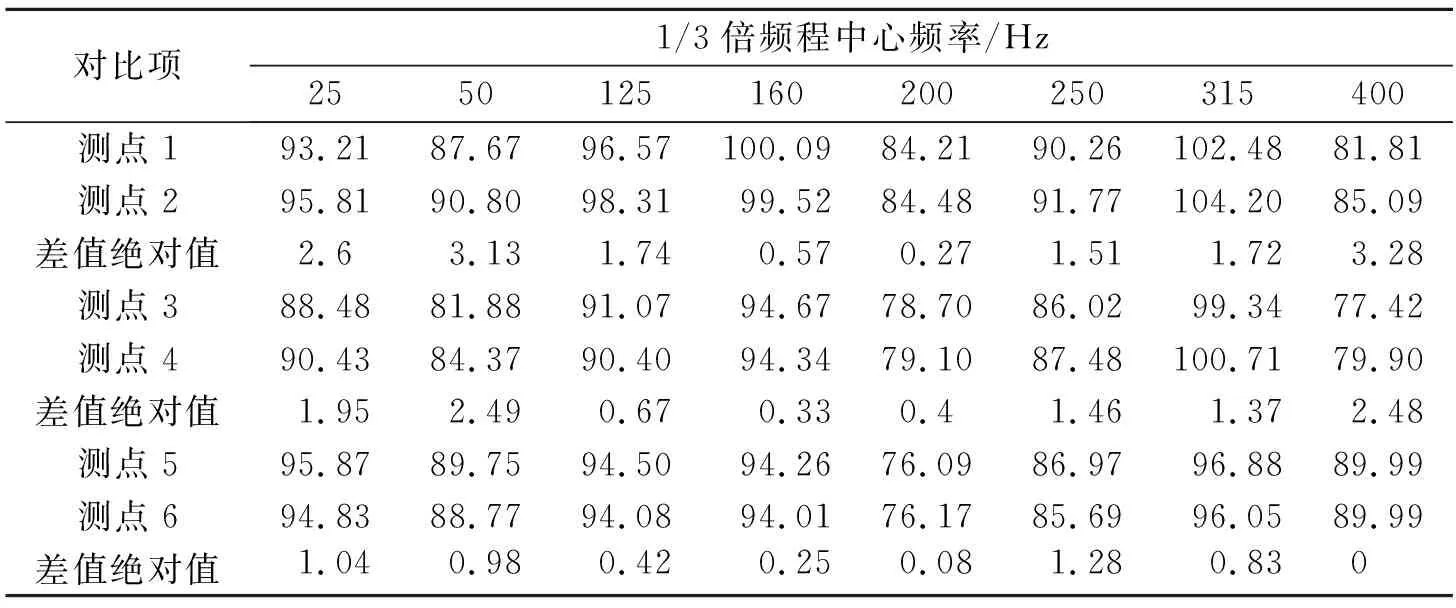
表4 相同機腳不同測點處振動加速度級對比 dB

從圖6還可看出，1、2、3、4測點的頻譜圖較相似，由于1、2測點，3、4測點分別在相同的機腳上，為方便比較，分別對比1、3測點頻譜圖中11個頻率點處的振動加速度級，見圖7。

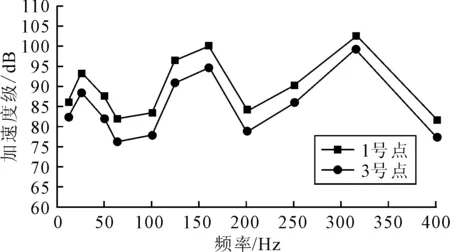
圖7 1、3測點處振動加速度級對比

由圖7可見，測點1每個頻率點的振動加速度級均大于測點3，所有頻率點處的差值平均值為4.89 dB，其中最小差值為3.14 dB，最大差值為5.78 dB。測點3所在的機腳靠近離心泵出口側，測點1所在的機腳遠離出口側，而離心泵蝸殼的截面直徑沿著流道逐漸變大，在出口達到最大，有擴壓的作用，因此水在蝸殼內流動時動能轉化為壓力能，流速減小，水壓增大，從而水的動量減小，測點3所在的機腳受到的流體激勵力小于測點1所在的機腳，最終導致測點1的振動比測點3強烈。

3.4 離心泵在不同工況下的振動特性

分別對0.60Q、0.80Q、1.20Q、1.40Q流量時的流動進行流固耦合模擬。提取各工況下測點1、3、5的振動加速度數據并進行傅里葉變換，3個峰值頻率(25.39、150.40、287.10 Hz)處的振動加速度級，見圖8。

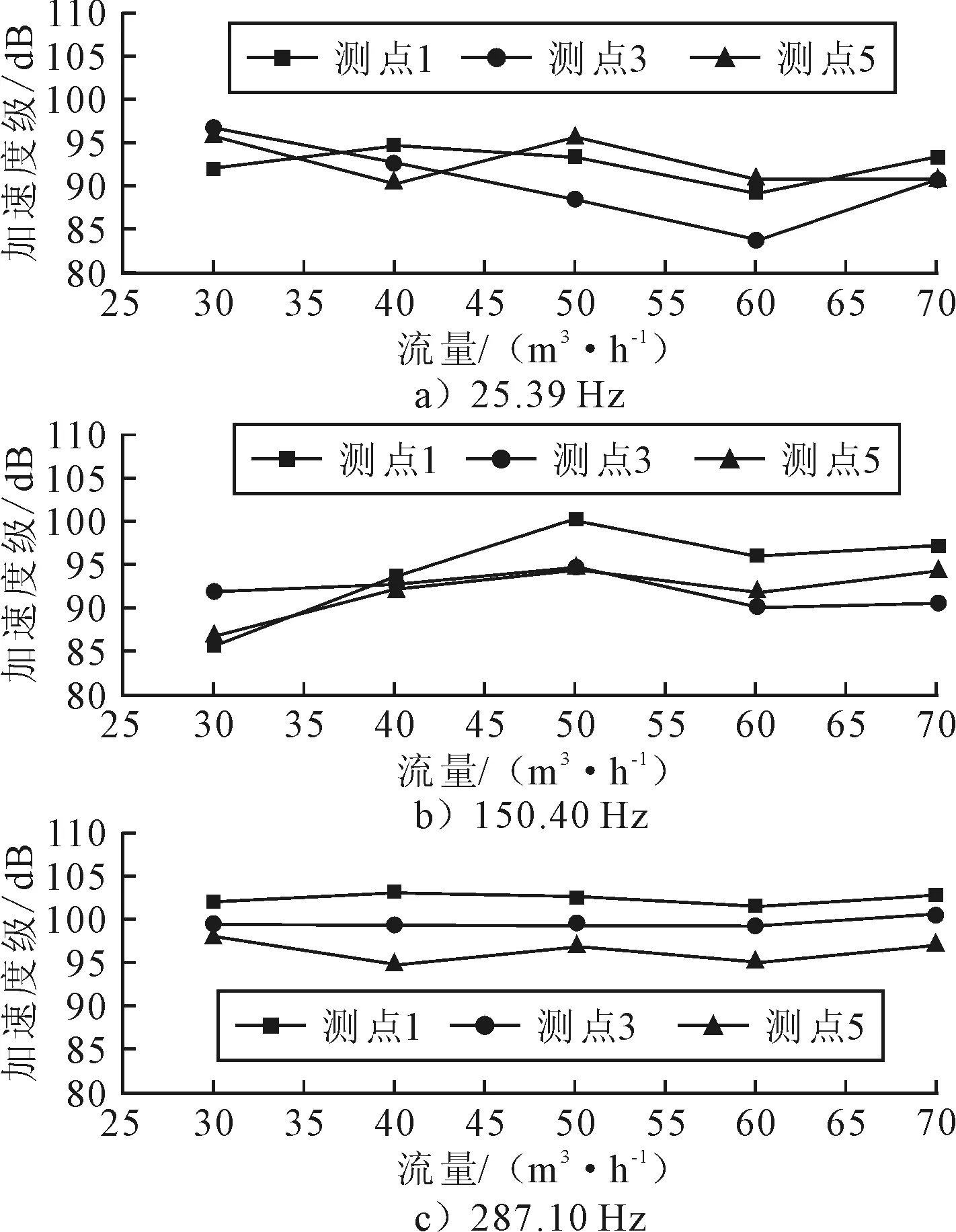
圖8 不同工況在峰值頻率處的機腳加速度級對比

由圖8可見，c)圖中的曲線比a)、b)圖中的平穩，其中25.39、150.40 Hz2個頻率點處加速度級變化量的平均值分別為3.95、3.34 dB，而287.10 Hz處的為1.18 dB，說明測點1、3、5在25.39、150.40 Hz處的振動加速度級隨著工況的變化而產生的變化比287.10 Hz處大。此外，a)、b)、c)中的曲線均在1.20Q時出現低谷，說明離心泵3個機腳的振動在1.20Q工況時呈現下降趨勢，結合前述Q-η曲線顯示離心泵在該工況下效率最高，因此建議同類型的離心泵工作時盡量采用1.20Q工況。

4 結論

1)在0～400 Hz內，離心泵的機腳在轉頻、葉頻以及葉頻的2倍頻處會產生強烈的振動，而且蝸殼一側的機腳在葉頻和葉頻兩倍頻處的振動比轉頻處的強烈，建議在實際安裝中針對轉頻、葉頻以及葉頻2倍頻處的振動采取減振措施。

2)在對離心泵機腳進行振動特性分析時，每個機腳只需提取1個節點的振動數據就可滿足分析要求，同時在對離心泵機腳的振動進行測試時，只需在每個機腳布置1個測點。

3)對于蝸殼處的機腳，由于蝸殼流道的擴壓作用，遠離離心泵出口側的機腳振動加速度級比靠近出口側的機腳 大4.89 dB，實際安裝中應著重對遠離出口側的機腳采取減振措施。

4)離心泵在轉頻、葉頻處的振動隨著不同工況而產生的變化比葉頻2倍頻處大，且3個機腳在轉頻、葉頻以及葉頻2倍頻處的振動在1.20Q工況時均呈下降趨勢，建議同類型的離心泵在工作時盡量采用1.20Q工況。

仿真計算時只考慮了轉矩轉速傳感器和三相異步電機的重力對離心泵機腳振動特性的影響，未能模擬實際工作狀況。因此，下一步應開展能精準模擬轉矩轉速傳感器和三相異步電機正常工作的建模方法的研究。