大動態光纖陀螺標度因數雙線性插值補償模型

姚俊杰，王 磊，陳杏藩，王金芳，劉 承

（1. 浙江大學 光電科學與工程學院，杭州 310027；2. 上海航天控制技術研究所，上海 201100）

光纖陀螺是一種重要的角速度傳感器[1]，在航空、航天、航海等軍用領域和地質、石油勘探等民用領域具有廣闊的應用前景[2]。對于高速旋轉的導航系統，如旋轉導彈、火箭彈的旋轉速度高達1500 r/min[3]，常規陀螺儀無法同時滿足測量范圍和測量精度的要求。近年來快速發展的大動態光纖陀螺技術具有測量范圍大、精度高等優點，是解決高速旋轉角度測量和圖像解耦的有效手段之一。

標度因數誤差是表征大動態光纖陀螺動態特性的重要參數之一[3]，其誤差大小直接影響光纖陀螺的動態精度。但是，受光纖環、光源等光電器件的影響，標度因數會隨溫度變化而發生改變[4]。對于大動態光纖陀螺，工作在高階條紋區間時，除了干涉條紋的對比度存在明顯的下降之外，光源光譜的非對稱會破壞干涉條紋的周期性，使標度因數的非線性誤差進一步惡化，影響陀螺的輸出精度[1]。在航空、航天等對動態精度要求較高的應用場合，需要對標度因數的溫度特性和非線性誤差進行補償。

關于標度因數誤差建模補償方面的研究，前人做了大量的工作。文獻[3]采用多項式擬合的方法對標度因數的溫度特性和非線性進行補償，在曲線具有多項式特征的情況時，多項式模型的補償精度高，但對測試誤差敏感，穩定性較差。文獻[5]提出并分析了光纖陀螺溫度與標度因數模型的遲滯現象，提升標度因數模型的補償效果，但未對標度因數的非線性進行補償。文獻[6]提出了基于多模型分段擬合的光纖陀螺溫度誤差補償方法。文獻[7-10]提出了多種基于神經網絡算法的標度因數溫度補償模型，得到了優于5′10-6的補償精度，補償精度較高，但這些方法需要大量的預先學習，并在使用時不斷更新模型，運算量大，實時性有待提高。大動態光纖陀螺的速率范圍大，一般超過了104(°)/s，模型樣本點多且規律性較差，尚未報道有合適的補償建模方法。

本文提出一種基于雙線性插值的補償模型，對溫度、角速率雙參量進行線性插值。標度因數誤差從補償前超過 1.3′10-3降低到小于 5′10-6，標度因數精度提升了兩個數量級，驗證了補償模型的有效性。所采用的算法復雜度低，補償精度高，易于工程實現。

1 大動態光纖陀螺標度因數誤差分析

大動態光纖陀螺基于數字閉環光纖陀螺技術，數字閉環光纖陀螺的結構如圖1所示。利用旋轉引起的Sagnac相移信號作為誤差信號反饋回系統，數字處理單元接收到誤差信號，通過D/A、相位調制器這條反饋通道產生一個附加的反饋相位將干涉儀固有的正弦響應轉換線性響應[1]，降低光纖陀螺標度因數在整個動態范圍內的誤差。

在數字閉環光纖陀螺中，干涉信號強度為：

大動態光纖陀螺根據閉環反饋控制，使總相位被伺服控制在零附近，如式(4)(5)所示：

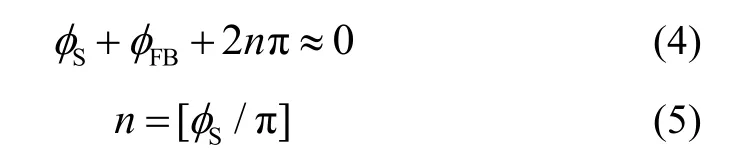
式中：n為所處的條紋級數，與產生的Sagnac相位相關。

光纖陀螺所用光纖環的長度及平均直徑會隨溫度改變而發生變化。光纖環幾何參數的溫度變化系數約在10-5/℃，且變化是線性的[11]。在溫度范圍（?40℃～ +60℃）內，引起的標度因數變化達到了10-3。

典型光纖陀螺所用的SLD光源波長的溫度漂移為10-4/℃[13-14]，對光源采用控溫可以有效提高波長穩定性，將光源波長的溫度系數減小到了1.7′10-6/℃左右。在?40℃～+60℃溫度范圍內引起的標度因數變化減小到 1.7′10-4。

大動態光纖陀螺跨條紋檢測，寬譜光源的特征也會影響標度因數的非線性。工作在高階條紋區間時，除了干涉條紋的對比度存在明顯的下降以外，光源光譜的非對稱會破壞干涉條紋的周期性，干涉響應發生變化，帶來了使標度因數非線性這一新特征。不同輸入角速率下，陀螺輸出存在變化為引起的光纖陀螺的標度因數相對誤差為[15]：

采用典型的超輻射發光二極管（Super Luminescent Diode, SLD）光源時，光源由于非對稱導致的光纖陀螺標度因數的變化如圖2所示。在0～104(°)/s的輸入角速率區間內，標度因數變化變化超過6′10-5。

圖2 標度因數與輸入角速率關系Fig.2 Relationship between scale factor and input angular velocity

2 雙線性插值補償模型

根據第1節的誤差理論分析可知，大動態光纖標度因數誤差主要由環境溫度和輸入角速率兩個因素影響。將標度因數K表示為：

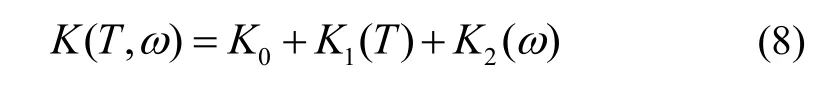
首先利用圖3中點1和點3的標度因數數據進行溫度插值得到點a的標度因數，利用點2和點4的標度因數數據進行溫度插值得到點c的標度因數，然后利用點a和點c的數據進行角速度插值得到點b的標度因數。計算過程如下：

根據雙線性插值算法對其余未知標度因數點進行計算，得到大動態光纖陀螺的標度因數補償模型。

圖3 標度因數網格示意圖Fig.3 Grid chart of scale factor

3 大動態光纖陀螺標度因數補償實驗

利用轉臺高精度的角位置基準搭建定角測試系統，對大動態光纖陀螺標度因數進行標定。對得到的模型樣本點進行雙線性插值，計算得到大動態光纖陀螺的標度因數補償模型。模擬實際應用環境，對所建立的大動態光纖陀螺標度因數雙線性插值補償模型的有效性進行驗證。實驗所用的 ZDH型大動態光纖陀螺[15]的速率范圍為±1.44′104(°)/s，零偏不穩定性為0.5 (°)/h，標度因數的重復性指標優于 5′10-6。根據實際應用需求，對溫度范圍?40℃～+60℃、角速率范圍0～7200 (°)/s條件下大動態光纖陀螺的標定因數進行標定實驗，并建立補償模型。

3.1 樣本點的獲取與建模

本文采用定角測試系統，利用轉臺角位置為基準進行大動態光纖陀螺標度因數標定，測試系統的結構框圖如圖4所示。采用FPGA同步采集光纖陀螺輸出數字量和高精度溫控轉臺輸出的角度脈沖，通過轉臺角位置信息獲得陀螺轉過的實際角度高精度計時器得到經歷的旋轉時間使用陀螺累積輸出數字量除以平均角速率得到陀螺在該溫度、速率點下的標度因數

高的標定精度有助于減少建模誤差。實驗所采用的高精度溫控轉臺的角位置定位精度為±32，轉臺的角位置精度達到4.6′10-6/圈，角位置定位精度與轉臺轉過的角度無關。轉臺轉動5圈以上時，位置誤差小于1′10-6。

圖4 標度因數標定實驗模塊框圖Fig.4 Function block diagram of scale factor calibration

式中，d為插值間隔。

根據二階連續導數的大小，選取樣本點的間隔，分別對溫度、角速率雙參量進行線性插值，計算得到三維網格圖，如圖5所示。該網格圖包含了溫度范圍?40℃～+60℃、角速率范圍0～7200 (°)/s條件下大動態光纖陀螺的標度因數數值，網格的交叉點代表了實測樣本點數據，其余數據點均由雙線性插值算法獲得。溫度引起的標度因數的變化超過了1.3′10-3，輸入角速率引起的標度因數非線性誤差達到了6′10-5左右。

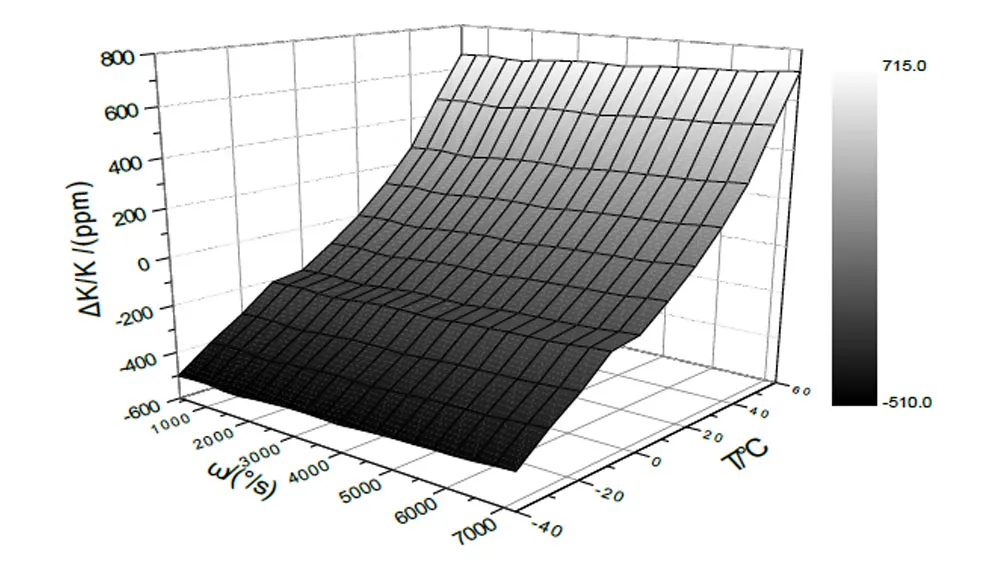
圖5 標度因數綜合模型三維網格圖Fig.5 There-dimensional grid map of scale factor integrated model

3.2 模型驗證

模擬實際應用環境，分別進行定角速率實驗和變角速率實驗。選取樣本點以外的溫度點、角速率點進行模型驗證。補償模型的評測系統如圖6所示。以轉臺輸出的絕對角度為基準，轉臺定位精度為± 32，測量陀螺累積輸出角度與轉臺絕對角度輸出的偏差，計算得到標度因數補償模型的誤差，綜合評估模型的有效性。

圖6 標度因數補償效果驗證實驗模塊框圖Fig.6 Function block diagram of scale factor compensation experiment

3.2.1 定角速率實驗

以一定的角速率間隔，設置角速率序列，進行不同角速率下的模型驗證。該方法可以對大動態光纖陀螺的標度因數進行分立檢驗，獲取不同角速率下補償模型的性能。

選取?25℃、15℃、45℃三個非樣本點的溫度點下1080 (°)/s、3600 (°)/s、4320 (°)/s、5400 (°)/s、6480 (°)/s、7200 (°)/s這六個非樣本點的角速率點進行定角速率實驗，將轉臺的角度基準與陀螺解算得到的角度進行對比，得到陀螺累積輸出角度偏差，將角度偏差除以轉臺的絕對角度輸出，計算得到標度因數補償模型的誤差。對所建立的雙線性插值補償模型在固定角速率情況下的補償效果進行驗證，實驗結果如圖7所示。結果表明雙線性插值補償模型在定角速率情況下輸出的角度偏差小于 5′10-6。

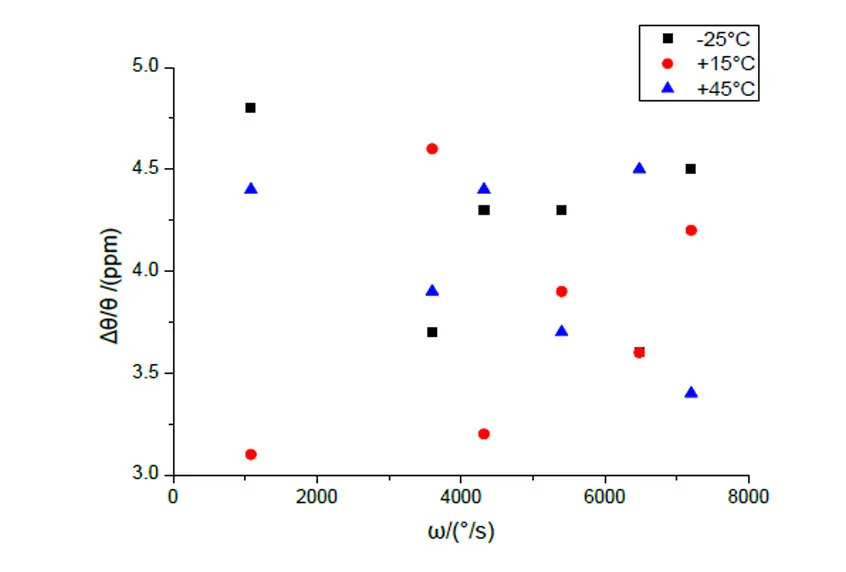
圖7 定角速率實驗結果Fig.7 Fixed-rate experimental results

3.2.2 角速率掃描實驗

以角速率掃描的方式，對陀螺進行角速率范圍為0～7200 (°)/s的測試，可以檢驗補償模型的綜合性能。相比定角速率測試，其更接近實際陀螺的實際應用。

選取?25℃、15℃、45℃三個非樣本點的溫度點進行角速率掃描測試，控制轉臺進行勻加速、勻減速轉動(0～7200 (°)/s)，模擬陀螺的實際應用情況。將轉臺的角度基準與陀螺解算得到的角度進行對比，對所建立的雙線性插值補償模型在變角速率下的補償效果進行驗證，測試結果如表1所示。結果表明雙線性插值補償模型在變角速率情況下輸出的角度偏差小于5 ′10-6。

表1 角速率掃描實驗結果Tab.1 Experimental results of angular velocity scanning

4 結 論

本文通過對大動態光纖陀螺標度因數的誤差分析表明，標度因數誤差主要受到環境溫度和輸入角速率大小影響。提出了一種基于雙線性插值的補償模型，對大動態光纖陀螺的標度因數的溫度特性和非線性進行綜合補償，在溫度范圍?40℃～+60℃、角速率范圍0～7200 (°)/s的條件下將標度因數誤差從補償前超過1.3′10-3降低到補償后小于 5′10-6，標度因數精度提升了兩個數量級，改善了大動態光纖陀螺的動態性能。該補償算法復雜度低，易于工程實現。