自主泊車路徑規劃一致性方法*

余卓平 夏浪 熊璐

（同濟大學，上海 201804）

主題詞：自主泊車 一致性路徑規劃 凸優化

1 前言

自主泊車路徑規劃作為智能汽車技術的典型代表，要求在極其狹窄的環境中找尋汽車從當前區域到指定停車位之間的可行駛路徑。輪式機器人所具有的不完整約束性質，以及車輛在復雜、狹窄環境里的碰撞檢測，都使自主泊車路徑規劃更具挑戰性。

在對當前泊車環境完全理解的基礎上，幾何法以其簡單、高效的特點，在路徑規劃中得到大量應用，它通過獲取當前車輛、環境障礙物、目標泊車位三者的幾何關系，采用直線或曲線求解車輛可行駛泊車路徑。具有開創性的幾何法當屬Dubins曲線[1]和可倒車Dubins曲線[2]。為彌補Dubins曲線曲率不連續的缺點，更多學者采用樣條曲線[3]、多項式曲線[4]以及回旋曲線[5]路徑規劃。然而，基于幾何的方法對環境要求高，通常每一套算法僅對應一種或一類環境，在停車環境日益復雜化的今天，幾何法已很難滿足自主泊車的“自主”需求，以快速隨機擴展樹（Rapidly Random Tree，RRT）或A*為基礎的各種變形搜索算法普遍用于輪式機器人的路徑規劃。然而，這些算法并未廣泛應用于自主泊車路徑規劃研究。Schwesinger U等人[6]在對歐洲代客充電（Valet Charge，V-Charge）項目的調研中提出將Hybrid A*算法應用于第3階段自主泊車路徑規劃，但該文僅限于思路，并未提及相關仿真及實車試驗。Kwon H等人[7]提出KPP（Korea University Path Planner）算法，對標基礎RRT算法，仿真結果表明，在泊車工況下，KPP算法在提供可選路徑寬度、曲率連續性等方面較基礎RRT算法有更佳表現。此外，一種基于數值優化求解的方法引起了關注。浙江大學的Li Bai[8]采用拉格朗日差值點的方法，將動態連續規劃問題離散為非線性優化問題，以數值求解的方式迭代求解出自主泊車可行路徑。然而仿真結果表明，該方法存在實時性差、優化過程初值敏感等缺點，實用效果并不理想。Zips P[9]與Gao H[10]等人分別針對泊車過程道路狹窄以及保障泊車過程安全性開展研究，核心部分同樣以數值求解的方式離散車輛狀態點，求解車輛路徑。

針對自主泊車工況，現有研究大多針對平行庫位與垂直庫位，鮮見關于斜庫位的泊車研究。根據我國公安部1988年頒布的《停車場規劃設計規則（試行）》，標準庫位包含不同角度的斜庫位。本文基于數值優化求解的特點，提出一種自主泊車路徑規劃的一致性方法，針對不同角度的庫位均可規劃出滿足需求的路徑，環境適應性強。

2 問題描述

2.1 問題背景

路徑規劃本質是兩點邊值問題的求解。針對泊車規劃的場景，統一約束方程，構造最優目標函數：

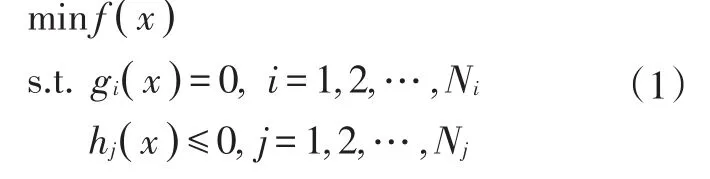
式中，gi(x)為等式約束；hj(x)為不等式約束；f(x)為優化目標。

針對一般的軌跡優化問題，優化對象包含T·K個變量，其中T為整個問題離散的狀態數目，K為優化對象狀態數。本文依次分析泊車問題中的等式約束、不等式約束以及優化目標，對整個泊車問題進行全面的數學表述。

2.2 等式約束

現實生活中，泊車過程車速較慢，本文忽略懸架作用，避免復雜的動力學模型，采用經典線性2自由度汽車運動學模型如圖1所示。

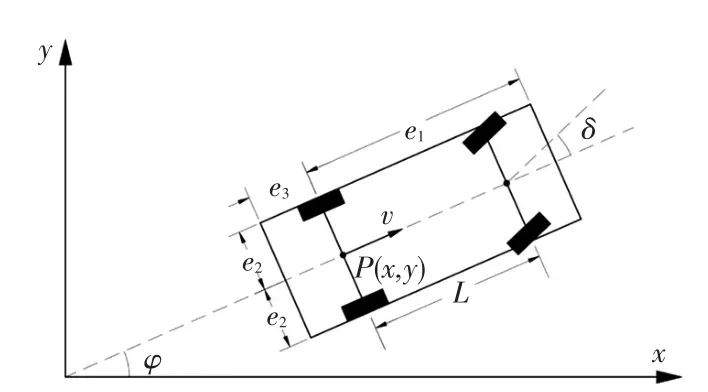
圖1 汽車運動學模型

其運動學方程為：

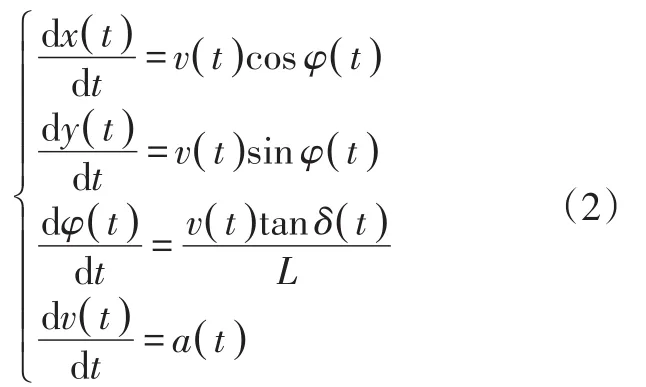
式中，(x(t),y(t))為車輛當前位置參考點（車輛后軸中心）P的坐標；φ(t)為車輛航向角；v(t)為車輛后軸中心線速度；δ(t)為前輪轉向角；a(t)為車輛切向加速度；L為軸距。

本文將整個泊車過程離散為(N+1)個狀態，假設任意兩相鄰狀態時間間隔top相等，離散后車輛的前后時刻狀態變換滿足：

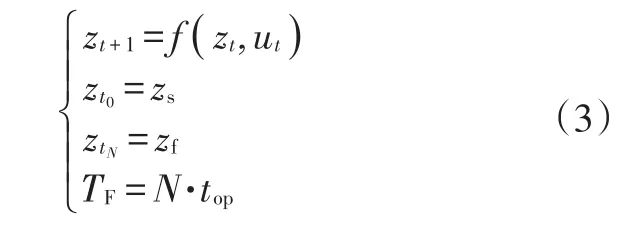
式中，zt∈Rnz為系統在（tt∈{t0,t1,…,tN}）時刻的所有狀態變量；zs為系統初始狀態；zf表示系統目標狀態；nz為狀態變量個數，包括x(t)、y(t)、φ(t)、v(t)；ut∈Rnu為系統在t時刻的輸入變量；nu為輸入變量個數，包括δ(t)、a(t)；Rnu→Rnz表示系統的狀態變換；TF為整個泊車過程所需時間。

2.3 不等式約束

假設障礙物OM與車輛E均為定義在R2上的真錐（Proper Cone），即含有非空內部且有界[11]。當前環境t時刻車輛占據的空間表示為Et?R2，障礙物占據的空間為OM?R2，OM=O1∪O2∪…∪Om。t時刻車輛與障礙物不發生沖突可表示為Et∩OM=?。通常上述問題是非凸的，因此需要對該問題進行進一步描述。

假設車輛與障礙物均為定義在R2上的多胞形（Poly?tope），那么，障礙物與車輛所占據的空間可表示為：

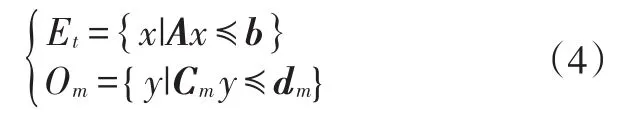
式中，A∈Rl·n；b∈Rl；Cm∈Rkm·n；dm∈Rkm；n為空間維度；l、k為組成凸集的超平面個數。

定義在R2上兩凸集Et、Om間的距離可表示為dist(Et,Om)=inf{||x-y||2|x∈Et,y∈Om}，如圖2所示，其中連接兩凸集的虛線為歐幾里得2范數（Euclidean Norm 2）最小值，即車輛與障礙物的距離。對于泊車過程的避障約束，通常設定車輛與障礙物之間的安全距離dmin，即dist(Et,Om)>dmin,?t∈{1,2,…,N}。進一步描述為：

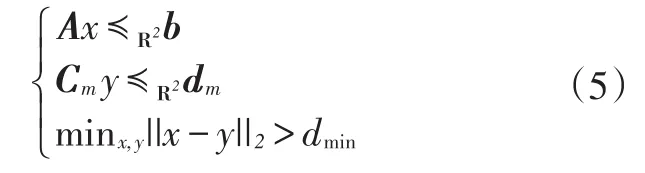
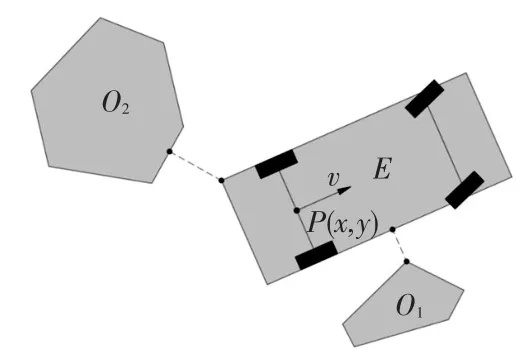
圖2 車輛與障礙物間距離示意

由于OM、Et的非空凸集性質，原問題滿足Slater條件，即?x∈Et，y∈Om，Ax=b，Cmy=dm，滿足強對偶性要求[11-12]，且對偶問題的最優解即原問題的最優解。上述不等式的對偶問題可以表示為 maxλ,μ{-bTλ-dTmμ}>dmin，ATλ+CTmμ=0，||ATλ||*≤1，λ?0，μ?0[13]，即：

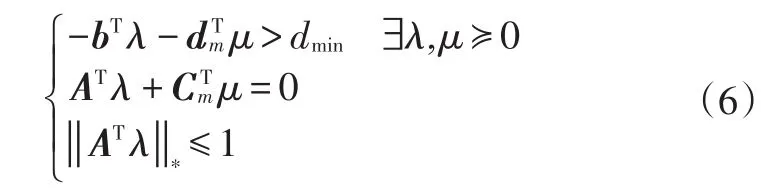
式中，λ、μ均為拉格朗日變量；||?||*為對偶范數。

針對障礙物，可通過獲得障礙物角點坐標求取矩陣Cm、dm。針對車輛本身，當車輛在P(xt,yt)點以航向角φ行駛時，車輛4個角點坐標分別為：

式中，e1、e3分別為車輛后軸到前、后端的距離；e2為車輛后軸中心至左、右端的距離。

將式（7）代入式（4），通過變換可得：

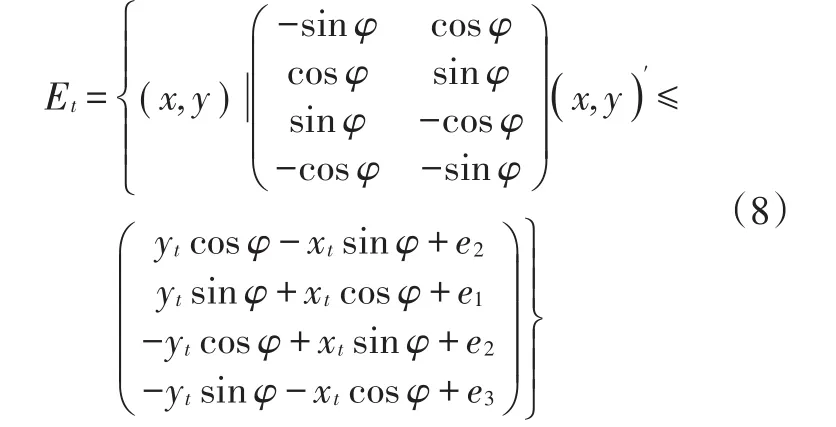
2.4 優化目標

文獻[8]針對自主泊車工況，將總時長TF設為優化目標，即整個過程用時最少、路徑最短。然而最短路徑在實際工況中可能并非最佳路徑。泊車過程希望在獲得最短路徑以及最小時長的前提下，車輛控制輸入應盡量小，在實際工況中表現為轉向角度盡量小、加速度盡量小，因此，本文設定目標函數為：

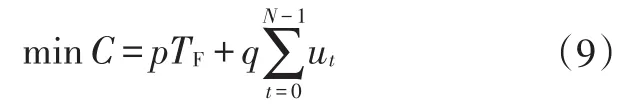
式中，ut表示每一個迭代步驟的控制量（前輪轉角δ(t)、切向加速度a(t)）；p∈R、q∈R分別為時間和控制量的權重，在實際仿真過程作為經驗值進行適當選取。

2.5 內點法

內點法（Interior-Point Methods）是一類解決線性或非線性凸優化問題的算法，通過引入懲罰函數，將約束問題轉換成無約束問題，隨后在迭代過程中不斷更新懲罰函數，將可行解“固定”在一定區域內，最終得到最優解。代表性的內點法有障礙法（Barrier Methods）和原始對偶法（Primal-Dual Methods）。無論面對線性規劃（Linear Programming，LP）問題還是二次規劃（Quadratic Programming，QP）問題，內點法在算法復雜度上都展示了極好的性能。

對泊車問題的統一優化框架包含上述等式約束、不等式約束以及優化目標，依據該優化框架，以及對當前環境的完整描述，運用內點法即可進行泊車路徑的求解。

3 仿真驗證

3.1 仿真描述

本文基于Ubuntu 16.04.4 LTS環境Atom JunoLab Plug-in:Julia-client/uber-juno對提出的方法進行仿真驗證，程序語言為Julia，處理器為Intel Core i5-7200U，最高睿頻3.1 GHz，內存8 GB，DDR4，2 133 MHz。數值優化求解器為開源優化庫IPOPT v3.12.9。仿真車輛模型采用某小型純電動轎車的參數，庫位大小參照國家停車場規劃設計規則，其余具體參數見表1。

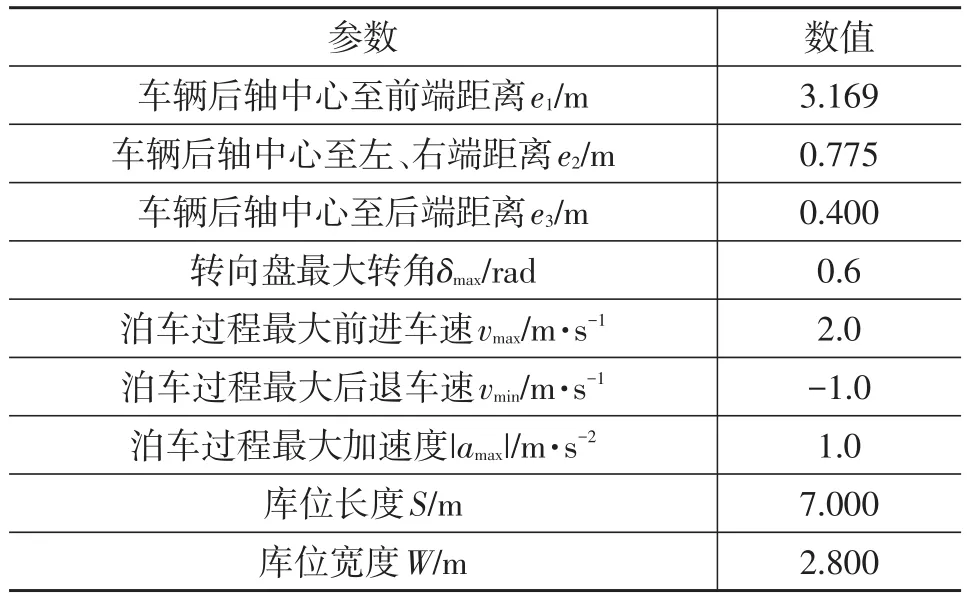
表1 泊車場景相關參數

3.2 仿真結果與討論

仿真泊車場景模擬實際生活中各種角度的庫位，與道路夾角分別為0°、30°、45°、60°、90°，仿真結果如圖3～圖7所示。其中，陰影矩形表示障礙物，在實際工況中可能表示非目標庫位、對向車道等。從圖3～圖7可以看出，針對各種角度的庫位，本文提出的一致性算法均可成功規劃出車輛起點至目標庫位的可行路徑，各車輛狀態與運用學參數均滿足車輛本身物理要求，滿足了自主泊車“自主”的要求。

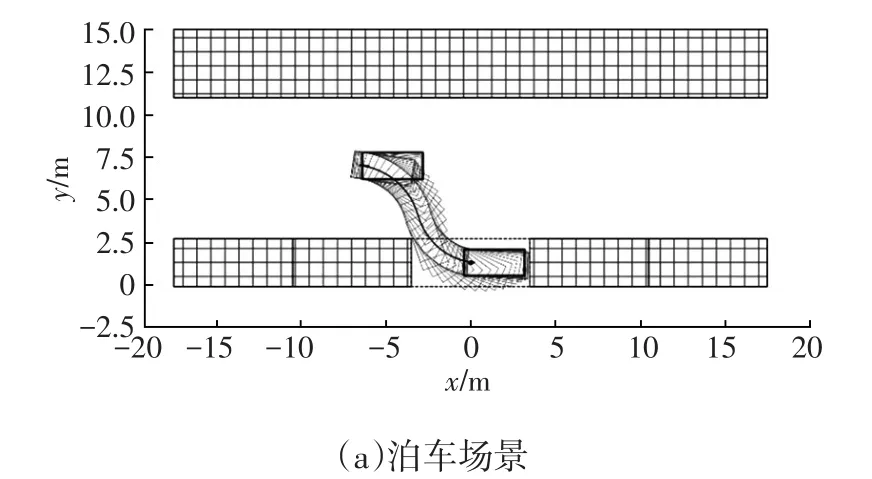
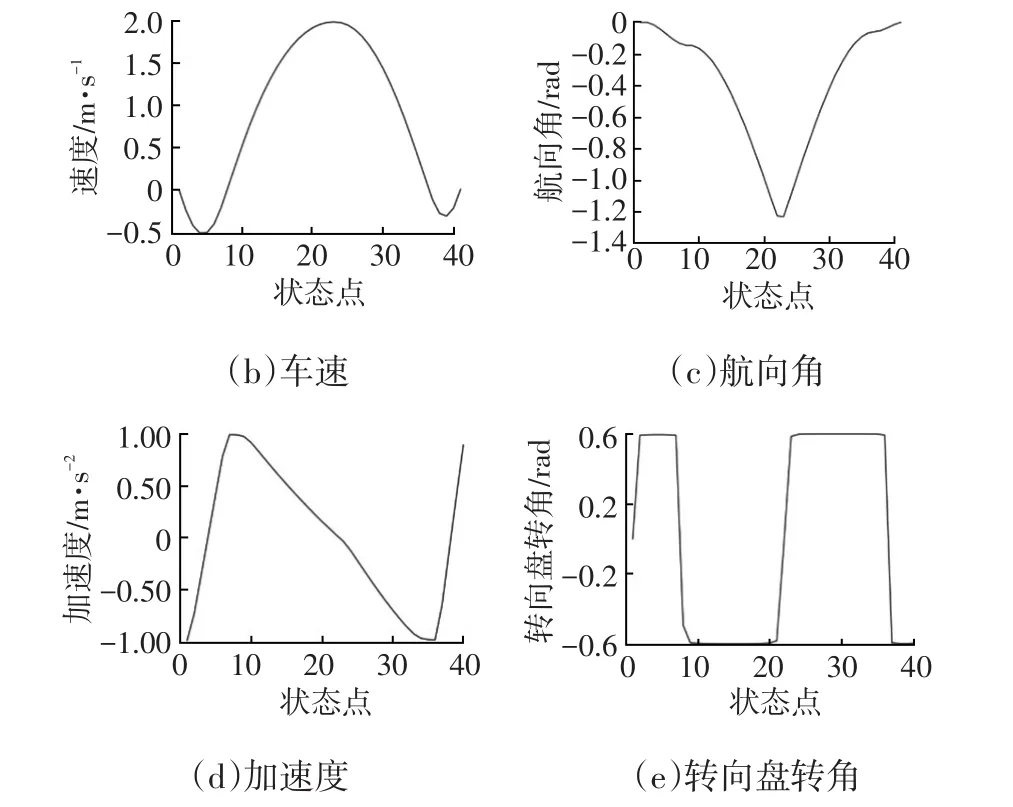
圖3 0°庫位角仿真場景及相應運動學參數

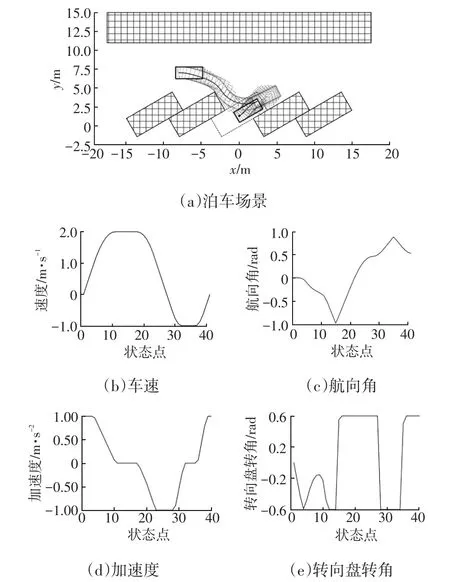
圖4 30°庫位角仿真場景及相應運動學參數

3.2.1 實時性

由于泊車工況車輛自身速度較低，且周圍通常無其他行駛車輛，與無人車路徑規劃相比，自主泊車路徑規劃實時性不足通常不會帶來安全隱患。然而，如果當前環境突然變化等情況發生，車輛不得不停止并等待計算出新的路徑，等待時間過長勢必極大影響用車體驗。表2給出了5個場景的計算總用時。

由表2可知，針對不同庫位角度，規劃時間有些許差異，總體上，實時性在可接受范圍，但并不能令人滿意。本次模型的一致性，使得問題所需要的求解器強大而可行，由于工具有限，本文采取數值求解的方法。該方法將連續變量進行離散化處理，變量個數為離散點個數與系統變量個數之積。龐大的變量數量給提升算法實時性帶來不小的挑戰。

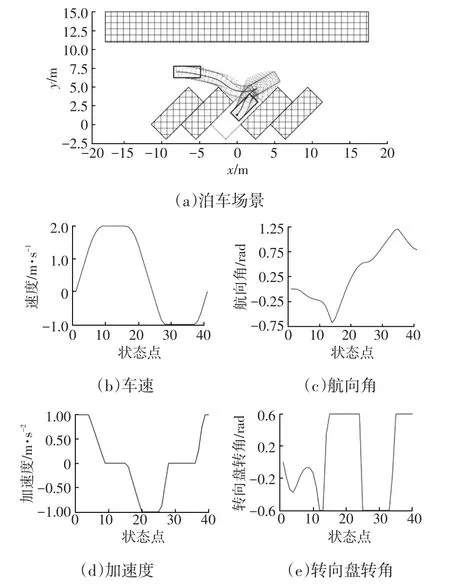
圖5 45°庫位角仿真場景及相應運動學參數

圖7 90°庫位角仿真場景及相應運動學參數

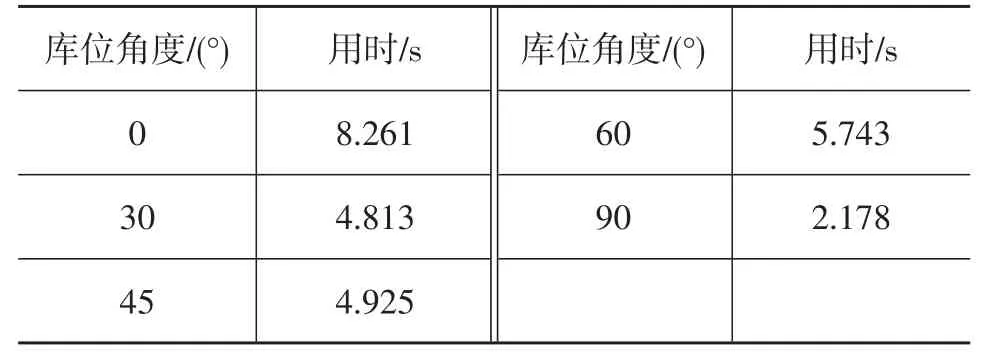
表2 不同場景規劃用時

眾所周知，對每一個優化問題來說，初值的選取極為重要。求解的過程是否收斂、求解所需的時間、求得全局解還是局部解，都與初值的選取息息相關。理想狀況下，所選取的初值應滿足上述所有約束，包括等式約束和不等式約束，然而由于車輛航向角的存在，適當的初值選取并不容易。本文首先假設泊車過程無任何障礙物，將線性離散起始點至目標點坐標值作為x(t)、y(t)的初值，其余變量φ(t)、v(t)、δ(t)、a(t)各值均置為零，求取該泊車場景的可行解，隨后將該解所對應的所有變量作為初值，求取障礙物存在時的泊車軌跡。

然而仿真表明，隨意的初值選取，使得算法的實時性并不理想。針對此問題，本文進行了進一步仿真，將上一個場景得出的解作為下一個場景的初值進行計算，如90°庫位角度得出的解作為60°的初值，60°庫位角度的解作為45°的初值，依次類推，90°采取最新60°庫位角求得的解。通過這樣初值選取，仿真時間如表3所示。

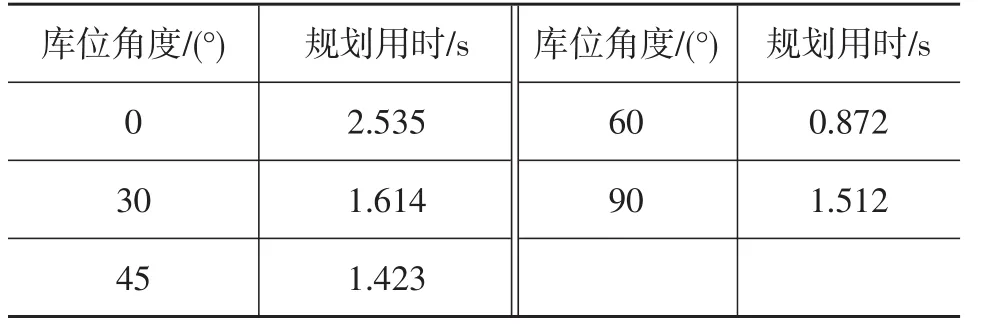
表3 改變優化初值后不同場景規劃用時

從表3可以看出，重新選取初值后，計算速度得到了顯著提高。這給實際泊車提供了一個新思路：為了提升泊車規劃實時性，可預先存取一定數量的解在規劃器中，針對實際具體泊車場景，提取與當前場景相近的離線場景所對應的解作為初值，在提高算法實時性的同時也極大地保障了問題的可收斂性。

3.2.2 車輛行為

由圖4～圖6可以看出，車輛泊車過程中，相比于調整自身位置，車輛希望更快向目標庫位靠近，遇到障礙物后再進行轉向操作。這與優化過程的初值密切相關，特別是車輛坐標初值。依上文所述，泊車過程初值選取的是不存在障礙物情況下的可行解，由于該解無視環境中障礙物，在當前迭代優化目標的驅動下，軌跡希望更快靠近目標庫位。由此，該初值所得出的最終解通常會有一段路徑離障礙物很近。實際工況中，駕駛員可能希望車輛距離障礙物較遠，然而從數值優化本身的角度看，所求出的路徑滿足不等式約束，且滿足優化目標的最小值，便是可行解。

4 結束語

本文驗證了自主泊車路徑規劃一致性方法在仿真環境中的可行性，尚未進行實車試驗。本算法要求車輛當前信息與環境信息準確可靠，然而實際情況下，傳感器輸入信息極有可能前、后時刻不一致。此時須在當前基礎上進一步提升算法實時性，根據更新后的輸入信息實時求取路徑。

此外，非線性數值優化求解器數量多達數十種[14]，本文僅討論Ipopt使用情況。針對自主泊車路徑規劃問題，是否有其他求解器在求解成功率、實時性等方面有更佳表現，值得研究。