毫秒激光輻照光學元件的多雜質損傷模型

王 斌,鄧 超,江修娥,潘云香,莫緒濤

(1.安徽工業大學數理科學與工程學院,安徽 馬鞍山 243032;2.南京理工大學理學院,江蘇 南京 210094)

1 引 言

隨著高功率激光器輸出能量密度的不斷提高,光學元件的抗損傷能力成為提高激光器輸出能量密度的制約因素。20世紀70年代以來,很多學者致力于激光誘導透明光學元件損傷的研究,發現通過實驗測試材料的損傷閾值常低于理論閾值[1]。為此,人們提出了多個模型來解釋這種現象,這些模型包括加熱雜質模型[2]、色心模型[3-4],熱電子碰撞電離模型[5]和多光子電離模型[3]等。其中,加熱雜質模型是解釋材料損傷的典型模型,它最初由Hopper提出,用于解釋光學玻璃激光損傷[6]。后來,加熱雜質模型較多地應用于薄膜激光損傷的解釋[7-8]。該模型假設材料中存在一定密度的雜質。其主要原因是:這些雜質的吸收系數大,在脈沖激光的照射下迅速升溫,使周圍的溫度瞬間高于熔點或沸點,這樣就在雜質周圍形成高溫微腔,且該微腔的范圍在熱傳導作用下不斷擴大；另外,材料內部溫度的不均勻分布使材料發生不同程度的熱膨脹,不可避免有某些部分材料的膨脹受到阻礙從而產生熱應力[9]。當材料中溫度大于熔點或應力超過拉伸/壓縮強度時,材料就發生破壞[10]。因此,在激光損傷光學元件的過程中熱吸收溫度和應力效應是激光損傷材料的主要機制[11]。

由于材料內部雜質的形狀、大小各異,為了對損傷形貌、損傷機理進行深入地理解,人們研究了包含已知性質的加熱雜質模型,如在研究薄膜損傷和玻璃損傷時假設雜質的形狀為球形[12]或圓柱形[7]；雜質的材質為金屬或非金屬(陶瓷雜質)[6]；雜質尺寸對損傷的影響[13]等。

有關激光損傷光學元件方面已經有了較多的研究,但大多研究主要集中在高功率短脈沖激光損傷方面,結果表明其損傷主要在淺表面極小范圍,損傷范圍為微米量級,損傷形貌近似為點狀[14-16]。有關短脈沖激光的損傷機理多利用前文所述加熱雜質模型進行解釋。然而隨著激光技術的發展,脈寬為毫秒量級的長脈沖激光越來越廣泛地應用于激光加工領域,其對光學元件損傷形貌和損傷大小均與短脈沖有很大不同,對應的損傷大小為毫米量級,損傷形貌近似為錐形[10,12]。此時用于解釋短脈沖激光的單個雜質加熱模型無法獲得與實驗現象吻合的理想結果,由于長脈沖激光的熱影響范圍遠大于短脈沖激光,必須考慮到光學元件內部相鄰多個雜質之間的相互熱傳遞及產生的熱團簇效應。

本文建立了毫秒激光輻射下的多雜質加熱模型,利用有限元法計算了涂有SiO2/Al2O3增透薄膜的K9玻璃光學元件在毫秒激光輻照下的溫度場和熱應力場,研究其溫度場和應力場分布的發展歷程,理論上分析毫秒激光的損傷效果,進而與實驗損傷形貌進行比較。數值模擬溫度分布與應力分布云圖顯示結果與實驗損傷形貌吻合較好。

2 模型建立及理論分析

激光與光學材料相互作用的過程中,光學材料中的雜質等缺陷能夠引起局部和周圍區域快速升溫,并隨之產生熱應力。因此,雜質使光學材料變得更容易破壞。在激光損傷光學材料的過程中,溫度場效應和熱應力起到很大的作用。

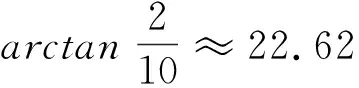
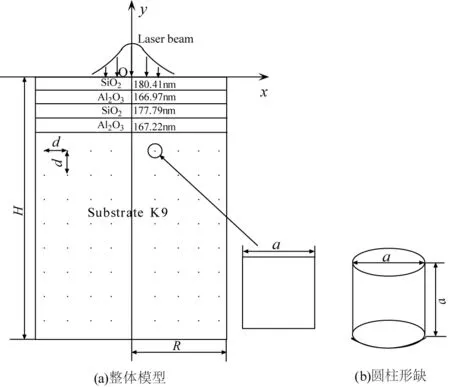
圖1 模型示意圖Fig.1 General View of the model

薄膜、基底以及缺陷對激光能量的吸收可表示為[17]:

T(x,y,0)=T0

(3)

式(2)和(3)分別為邊界條件和初始條件，T(x,y,t)為t時刻(x,y)處的溫度；Ci、ρi、ki分別為比熱容、密度和熱導率。下標i取1、2和3,分別代表薄膜、基底和缺陷；T0=293.15 K為環境溫度；Qi(x,y,t)為熱源,薄膜和基底的熱源可表示為:

Qi(x,y,t)=αi|E(y)|2niIlaser(i=1，2)

(4)

雜質的熱源可表示為:

Q3(x,y,t)=α3|E(y)|2n3Ilaser×exp{-α3[a-(h+y)]}

(5)

式中,αi為材料的吸收系數；E(y)為材料中的電場強度分布,可由麥克斯韋方程組和薄膜特征矩陣得到；ni為材料的折射率；h為雜質距樣品上表面的距離,其大小與雜質的位置有關；Ilaser為激光入射功率密度,可表示為:

Ilaser=I0f(x)g(t)

(6)

其中,I0為峰值功率密度;f(x)和g(t)分別為激光脈沖的空間和時間分布,且:

式中,R0為光束半徑;τ為脈沖寬度。

材料吸收激光能量后溫度升高,由于Pt雜質的吸收系數遠大于玻璃基底以及激光光束的空間分布不均勻,材料內部各個部分的溫升不同,從而產生熱應力。溫度變化產生的應力、應變則用熱彈性力學的原理計算。熱彈性方程可表示為[18]:

基本關系式可表示為:

幾何變形關系可表示為:

其中,e=εx+εy+εz,e=(σx+σy+σz)(1-2μ)/E,E、μ和β分別為楊氏模量、泊松比和線性膨脹系數；ε、σ和u分別為應變、應力和位移；下標x、y、z分別代表三個方向上的應力和應變；xy、yz、zx分別代表不同方向上的剪應力和剪應變。

忽略雜質對光場的調制,采用有限元法計算薄膜和K9玻璃中的溫度和應力場分布,計算所需參數在表1中給出[10]。

表1 計算所需參數值Tab.1 Parameters used in the simulation

3 計算結果和討論

3.1 溫度場和應力場的分布

圖2為作用于光學元件的激光能量為21 J時的溫度場分布圖,(a)～(d)分別對應于t=0.1 ms、0.3 ms、0.7 ms、1.0 ms時刻,圖中標出了T=293.15～638.15 K、638.15～983.15 K、983.15～1328.15 K、1328.15～1673.15 K區域。在激光作用時間內,溫度隨作用時間的增長而增大,這些區域的形狀近似為錐形,這與光束在元件中的分布有關。K9玻璃的熔融溫度為1673 K,從圖中可以看出靠近薄膜部分的K9玻璃基底溫度達到了熔點,這主要有兩方面的原因,一方面,該部分靠近激光光束焦平面,能量密度較其他各處大,吸收的熱量更多,溫度上升的幅度也就更大；另一方面,薄膜對激光的吸收強度大于玻璃,薄膜內的溫升更大,薄膜通過熱傳導加熱玻璃,致使靠近薄膜部分的玻璃溫度進一步上升。此外,由于Pt缺陷的吸收系數達到7×107m-1,在激光作用過程中,這些缺陷大量地吸收激光能量使自身溫度迅速上升,并通過熱傳導的作用在其周圍形成高溫“微腔”。

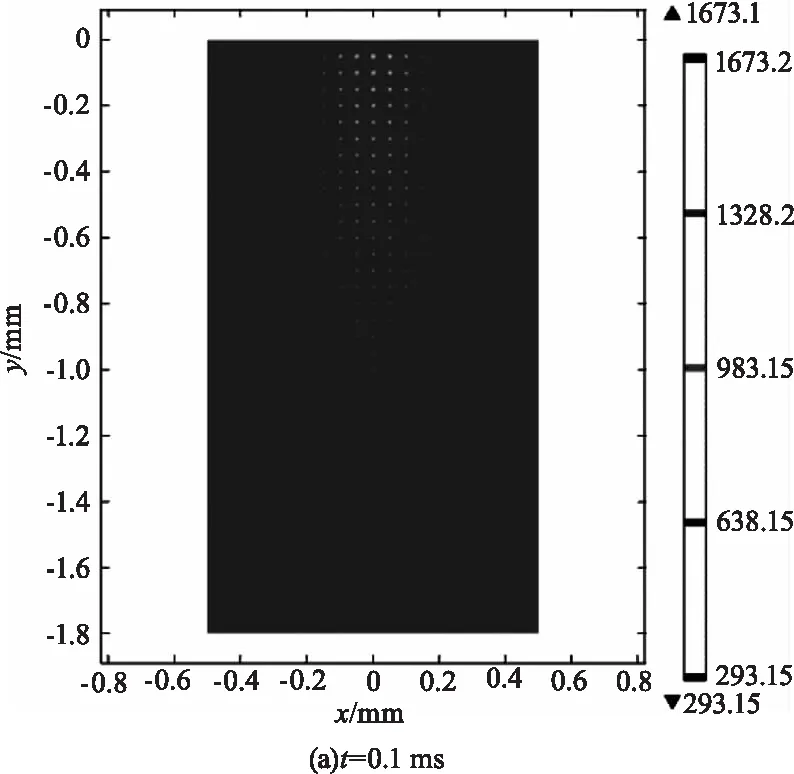
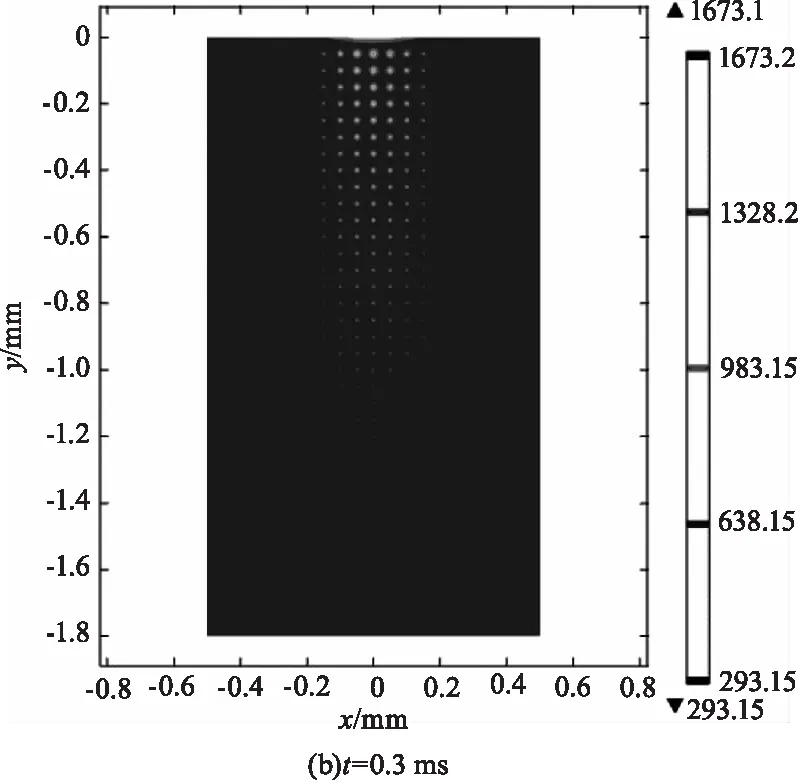
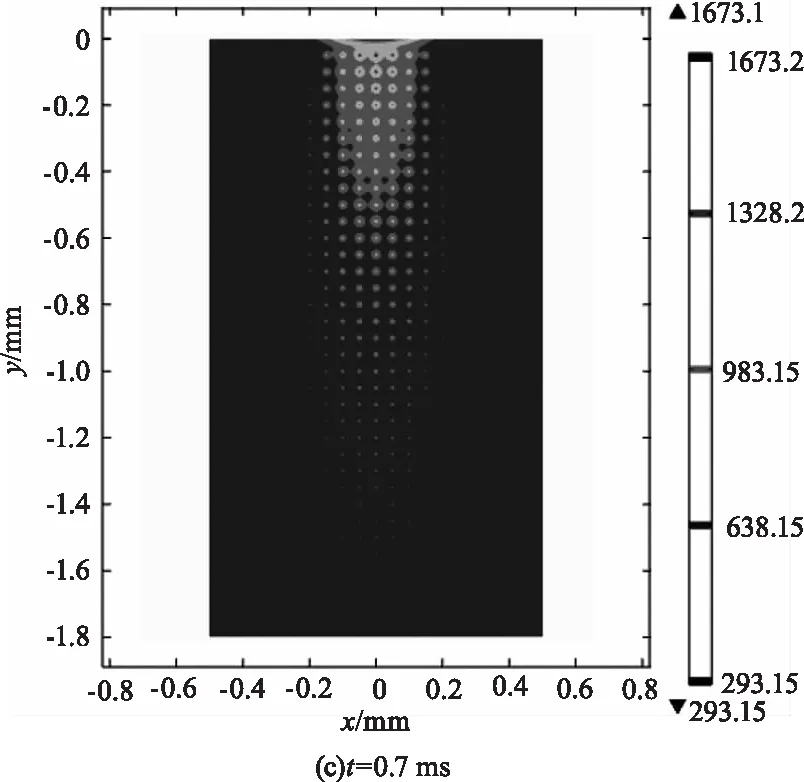
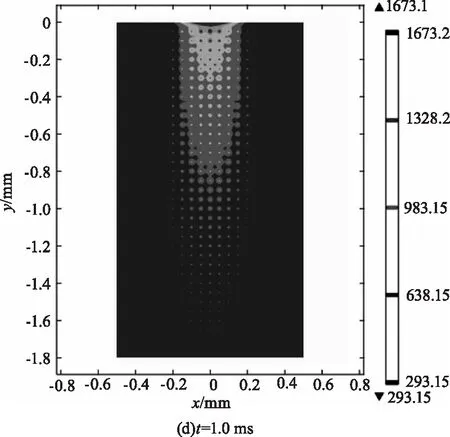
圖2 溫度分布圖Fig.2 Temperature field distribution

溫度的升高使材料內部產生不均勻膨脹,進而產生壓縮應力和拉伸應力。圖3為相同能量密度下,樣品內部x向熱應力分布圖,圖中負值代表壓應力,正值代表拉應力。激光照射過程中,K9玻璃與激光作用部分因溫度升高而引發熱膨脹。以Pt雜質為中心形成的高溫微腔由于溫升幅度高于周圍玻璃,熱膨脹受到周圍的限制,從而在微腔內形成壓縮應力。在Pt雜質周圍直徑約為1 μm的范圍內,壓縮應力大于K9玻璃的壓縮強度σC=650 MPa,玻璃會產生微小破損。微腔周圍外部則相應形成拉伸應力,當拉伸應力值大于玻璃拉伸強度σT=28 MPa時,就會產生裂紋。

圖3中分別標出了拉伸應力為28 MPa和56 MPa的等值線。從圖中可以看出,在缺陷間隔處形成一個個拉伸應力大于拉伸強度的小區域,這些小區域最先遭到破壞。值得注意的是,在圖3的(b)-(d)中,基底的下表面有一部分的應力值超過28 MPa,也就是說這部分將會遭到破壞。

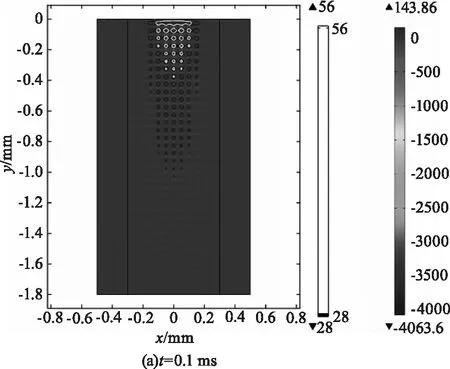
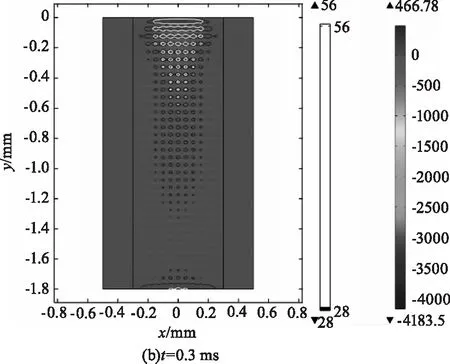
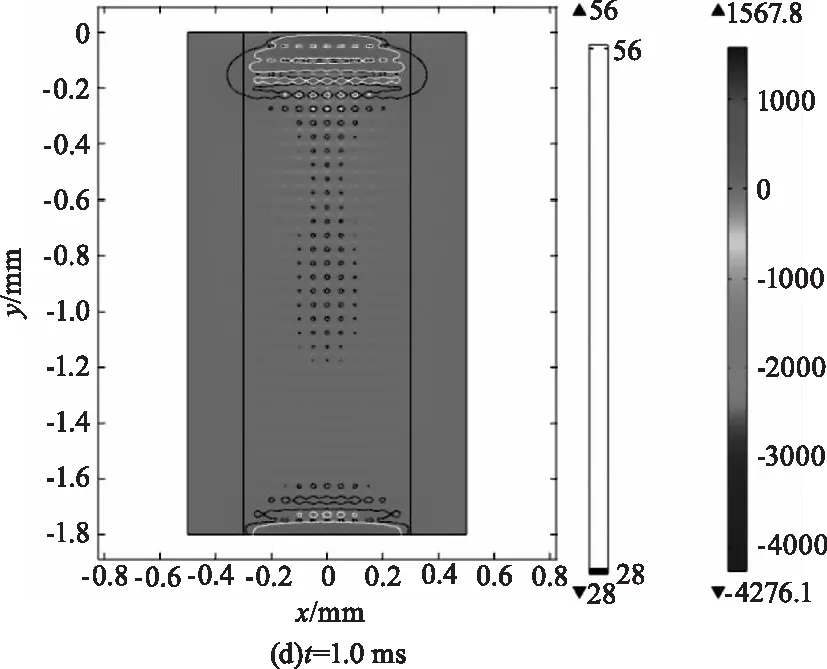
圖3 x向應力分布圖Fig.3 Stress distribution alongx direction

從以上數值模擬的溫度與應力分布云圖中可以看出,該光學元件在毫秒長脈沖激光輻照下,不僅前表面將出現損傷,后表面也將出現損傷。前表面的損傷由于溫度和應力的共同作用導致,后面主要由于應力所致。

3.2 分析與討論

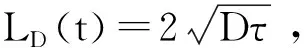
雜質周圍形成的微腔的平均溫升可表示為[9]:

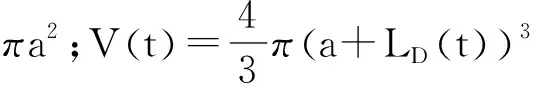
由此可以看出,對于納秒激光,只有雜質附近的區域受到影響,并且微腔的溫度達到105K量級,說明該部分已經熔融氣化甚至可能產生等離子體；而對于毫秒激光則完全不同,由于毫秒激光的持續時間長,雜質周圍很大一片區域的溫度都將受到影響。這也是對于毫秒激光損傷機理探討需要引入多雜質模型的原因,且我們發現,雖然長脈沖激光熱影響范圍大,但由于熱擴散效應,雜質團簇周圍的總體溫升小,因此不易產生熔融損傷,應力損傷成為長脈沖激光損傷不可忽略的一個因素。

4 實驗損傷形貌特征

本課題組進行了相關的毫秒長脈沖激光損傷實驗。實驗裝置如圖4所示,所用為一Nd3+∶YAG毫秒級脈沖可調脈沖激光器,波長1064 nm。實驗中調節并固定脈沖寬度為1 ms。激光器發出的光束經過分光器后被分成兩束,一束經透鏡聚焦到樣品表面,一束到達能量計進行測量。被輻照樣品為K9玻璃基底上鍍SiO2/Al2O3抗反射膜層的光學元件,元件結構及厚度尺寸與圖1所示一致。

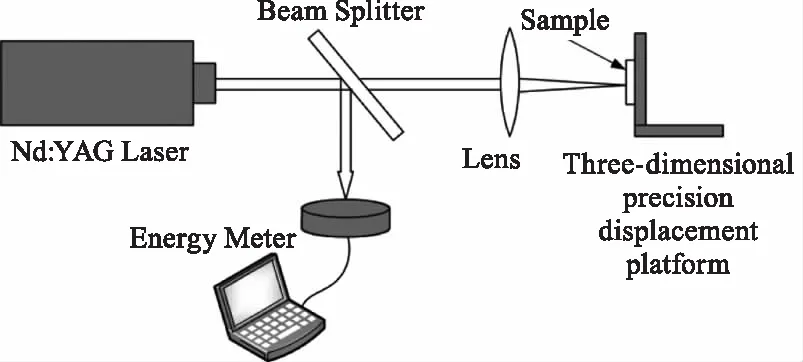
圖4 激光損傷實驗裝置Fig.4 Experiment setup of laser induced damage

圖5為實驗獲得的損傷形貌照片。從這些損傷照片可以看出,損傷形貌近似為錐形,且下表面也有不同程度的損傷。這一損傷特征區別于短脈沖激光的情況,同時也是單雜質模型無法得到的。將多雜質加熱模型的數值模擬溫度分布與應力分布云圖結果與實驗結果進行比較可知,從損傷形貌上看,二者具有一定的吻合度。

圖5 激光損傷形態圖Fig.5 Cross section photos of laser induced damage

需要附加說明的是,數值模擬云圖與實驗損傷形貌仍然存在一些差異,如損傷尺寸,損傷深度與強度等。這主要是由于多雜質模型中作了一些簡化或近似所致:①未考慮材料參數隨激光作用過程中溫升的變化；②未考慮雜質本身對光場的影響；③未考慮相變或裂紋產生對后續激光作用的影響。數值結果顯示,在激光作用初期(如圖3(a)所示),已有部分區域應力值超過玻璃所能承受的臨界強度,也就是說,這些部分已經遭到破壞。事實上,這些破壞處將使局部光場增強或局部光吸收增強,進而增強后續激光的破壞效應,在后續激光的作用下,原先遭到破壞的小區域將加速擴張。由于數值模型中并未考慮該動態過程影響,因此,實際過程中后續損傷的擴張速度與強度可能會強于數值模擬結果。這些都是今后研究對多雜質加熱模型進一步優化的有效途徑。

5 結 論

本文建立了毫秒激光輻射下的多雜質加熱模型,對涂有SiO2/Al2O3增透薄膜的K9玻璃光學元件在毫秒激光輻照下的溫度場和熱應力場進行了數值模擬,分析了溫度場和應力場分布的發展歷程,結果表明在毫秒激光作用下,微小雜質團簇能夠導致毀滅性的損傷,且損傷同時出現在元件的前后表面,前表面為溫度與應力效應共同作用,后表面為應力效應主導。數值模擬結果與實驗結果吻合良好。本文所建立的多雜質加熱模型可以為長脈沖高能激光損傷光學元件機理的進一步研究提供幫助。