旋風除塵器最優化設計及CFD數值驗證

郗 元 ，霍 浩 ，代 巖

1 引言

隨著我國工業的迅猛發展，工業生產過程中產生的粉塵已成為造成霧霾的主要原因。究其根本必須做好對粉塵源頭的控制，這是最直接也是最有效的治理方法[1]。旋風除塵器作為高效率、低能耗的除塵設備，廣泛應用于能源及環保行業中。文獻[2]設計了一種用于回收煙氣余熱的套管換熱式旋風除塵器，熱回收量可以提高（1.33～3.06）倍。文獻[3]通過引入噴霧降塵技術提高了旋風除塵器的除塵效率，并結合MATLAB對其進行了不同壓力的計算。文獻[4]結合神經網絡對旋風分離器進行了多目標優化研究。

上述研究均從不同角度提高了旋風除塵器的性能，但很少有學者針對全局結構參數進行整體優化分析。通過建立除塵效率理論計算模型，綜合考慮各結構影響參數，并結合MATLAB進行尋優計算，對新結構下旋風除塵器內部流速、壓力及除塵效率進行數值模擬分析，驗證理論模型，確定最優結構參數的可行性。

2 物理模型

某型號旋風除塵器結構示意圖，如圖1所示。其主要結構包括旋風除塵器入口高度a、入口寬度b、筒體高度H；出氣口直徑Dc、插入筒體深度 L；筒體直徑 D0、高度 Hc；排灰口直徑 Dd。

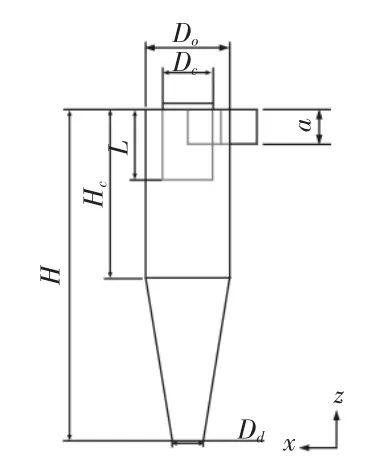
圖1 旋風除塵器結構示意圖Fig.1 Structure Diagram of Cyclone Dust Collector

3 數學模型構建

選取除塵效率作為旋風除塵器分離性能的優化目標，并結合Leith-Licht設計法[5]，建立數學模型。

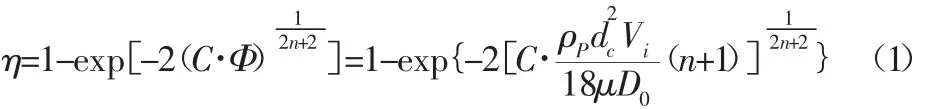
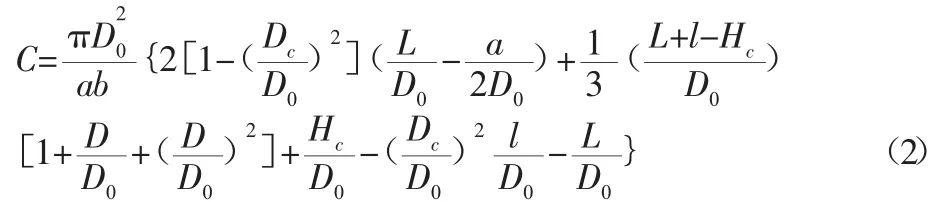
結合井伊谷鋼一的普通直入型旋風分離器的壓力損失公式[6]：

式中：K—常數，取16；Vi—進風口速度；ρ—氣體密度。

將Vi=Q/ab代入式（3），并整理得

結合除塵器設計手冊等[7]，旋風除塵器各結構參數應滿足如下要求：入口寬度與排氣管壁到器壁的距離應該滿足以下關系：

旋轉渦流延伸到的位置應到達錐筒底部，即滿足以下等式（6）關系

令D20/ab=M，則CΦ=CM·Φ/M，對于任何固定值Φ/M，都代表著一定性質的粉塵和運載介質（如空氣）的流動情況。當CM取得最大值時，除塵效率ηi取得最大值。故把G=CM作為優化設計得目標函數，通過整理得出目標函數表達式如下：

優化設計所需約束條件如下：

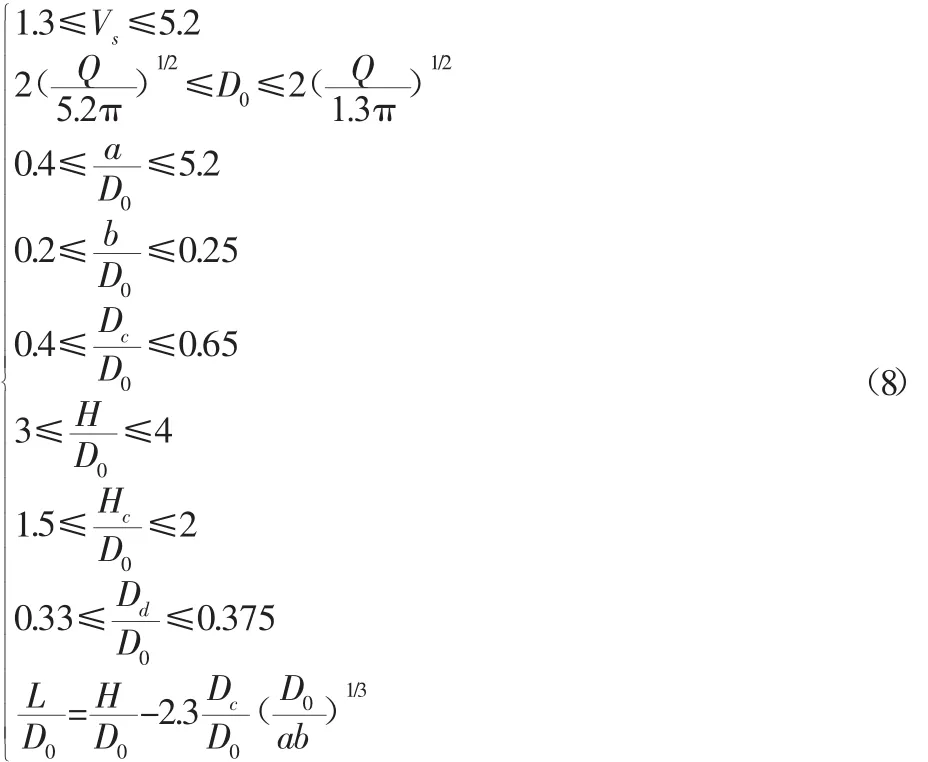
在設計旋風除塵器時，通常處理風量Q和壓力損失ΔP為給定量，通過目標函數表達式不難看出，在Q和ΔP給定的情況下，目標函數的大小只與旋風分離器的各結構尺寸有關，故選取優化設計變量X如下：

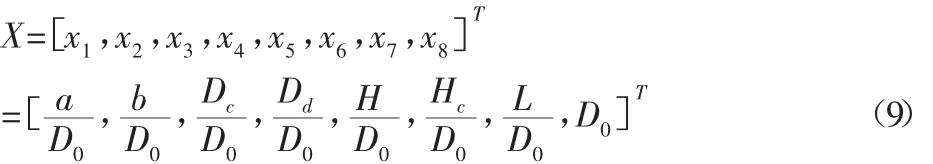
結合MATLAB對該非線性極小值優化問題進行求解，計算結果，如表1所示。

表1 旋風除塵器最優結構計算結果（單位：mm）Tab.1 Optimal Structure Results of Cyclone Dust Collector（unit：mm）

MATLAB優化得到的目標函數最大值為G=4431.0430，而G=C·M=C·D20/ab，從而求得幾何特性因數C=354.4834。結合式（1）進行分級除塵效率計算，以粉塵粒密度為1960kg/m3，氣體粘度μ為1.72×105Pa·s，室溫T為293.15K。選用文獻[8]的顆粒粒徑分布模型，代入各粒徑值和各已知物理量值得到的分級效率列，如表2所示。

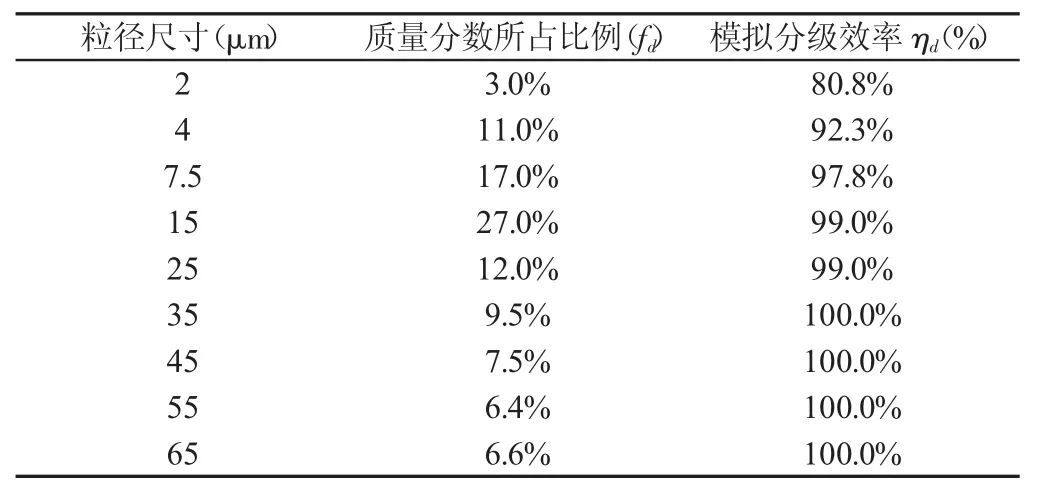
表2 理論計算各粒徑分級效率Tab.2 Theoretical Value of Fractional Efficiency for Each Particle Size

旋風除塵器的總除塵效率，如式（10）所示。

式中：fd—不同粒徑尺寸的質量分數所占比例；ηd—分級除塵效率因此，求得旋風除塵器總的除塵效率為97.1%。

4 CFD數值模擬驗證

根據最優結構參數進行流道模型建立，并對其進行劃分網格處理。經過網格無關性分析后，最終確定網格數量為597292，網格模型，如圖2所示。

圖2 旋風除塵器網格模型Fig.2 Cyclone Dust Collector Mesh Model

邊界條件設置：速度進口，速度為12.76m/s，入口速度分布均勻且垂直于入口截面；排氣口為壓力出口，壓力值為標準大氣壓；壁面為無滑移壁面。考慮旋風除塵器內部的氣固兩相流動，因顆粒相與氣相比所占體積分數較小且低于10%，可采用DPM模型[9-10]。

算法選取：湍流模型采用標準k-ε湍流模型[11]；對流項采用適用于強旋轉流具有三階精度并能減少假擴散的QUICK格式；壓力梯度項插補格式的選取最能真實地反映旋風分離器內的強旋流場特性的PRESTO格式；數值計算方法為非交錯網格下的SIMPLE算法。

塵土顆粒主要是依靠旋轉時受到的離心力來實現分離，因此在旋風分離器的速度場中切向速度占主導地位。旋風除塵器不同Z軸高度位置的切向速度隨橫坐標x的變化曲線，如圖3所示。從圖中可以看出，在中心軸兩側隨半徑的增大，切向速度也隨之增大該曲線在中心軸兩側分別存在一個峰值，近似為對稱形式。

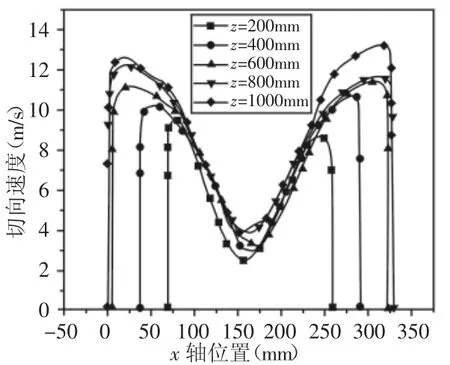
圖3 切向速度分布Fig.3 Tangential Velocity

從切向速度的分布曲線可以看出，切向速度呈現為駝峰狀，即在軸心處的切向速度最小，在軸心兩側分別有以個峰值，并且該峰值出現在排氣管壁位置附近，切向速度具有較好的軸對稱性，并且軸心與排氣管壁面之間，切向速度的大小沿半徑方向隨半徑增大而增大，而在排氣管壁面外部流場區域，隨著半徑增大而減小，排氣管壁面位置處剛好是切向速度峰值。

圖4 y=0截面速度云圖Fig.4 Section Velocity y=0

圖5 y=0截面靜壓力云圖Fig.5 Section Static Pressure y=0

y=0截面速度云圖，如圖4所示。從圖中可以看出，含塵氣流流入后從旋風除塵器的入口開始做加速運動，氣流繼續加速流動進入旋風除塵器的圓柱形筒，在轉彎時速度達到峰值。隨后氣流沿筒壁作切向速度逐漸減小的圓周運動。排氣管中間區域存在明顯的低速區域，由于此處速度較低，流場中夾帶的粉塵顆粒在這個停留區域容易出現沉積現象。另外，從該截面可以看出，由于排風管底部具有較大的切向速度，這便解釋了升氣管底端為什么容易發生短路流，從而影響了分離性能[5]。旋風除塵器y=0截面的靜壓云圖，如圖5所示。從圖中壓力分布可以看出靜壓沿徑向的分布比較均勻，并且在軸兩側比較對稱，靜壓的大小沿著半徑方向由內到外，壓力逐漸增大，并且壓力隨半徑變化的變化率較大。中心軸線附近靜壓值相對入口處的靜壓值要小得多，并且中心軸區域靜壓力值為負，負壓區很好的解釋了旋風除塵器的中心處于真空狀態。沿著軸向來看可以發現，由于在強旋流場中，靜壓同樣受切向速度的影響較大，所以軸向上靜壓值基本沒有變化。另外兩個速度分量對靜壓值的影響相對較小。旋風分離器中心軸線處的靜壓值在整個流場中相對是最低的，整個中心低壓區一直延伸至排塵口端，這便是旋風除塵器錐體底部容易發生滯流或返流問題的原因，如果灰斗底部密封不嚴，由于中心軸處于負壓區很容易倒吸外界氣流，這就直接導致了旋風除塵器的分離性能變差。

注入顆粒計算除塵效率時，顆粒射流源類型選用面射流源，面射流源的顆粒初始位置設定在速度進口端面上，并使入射點的位置在進口端面上均勻分布。采用單顆粒相噴射注入法，即每次注入一定直徑的單種顆粒。噴射點源為160個，每個點源產生10個顆粒，對總計1600個粒子進行追蹤。設置入口噴射速度為12.76m/s，分9次注入流場中顆粒分別檢測上排氣口逃逸粒子數，從而計算出各分級效率。各粒徑分級效率數值模擬結果，如表3所示。

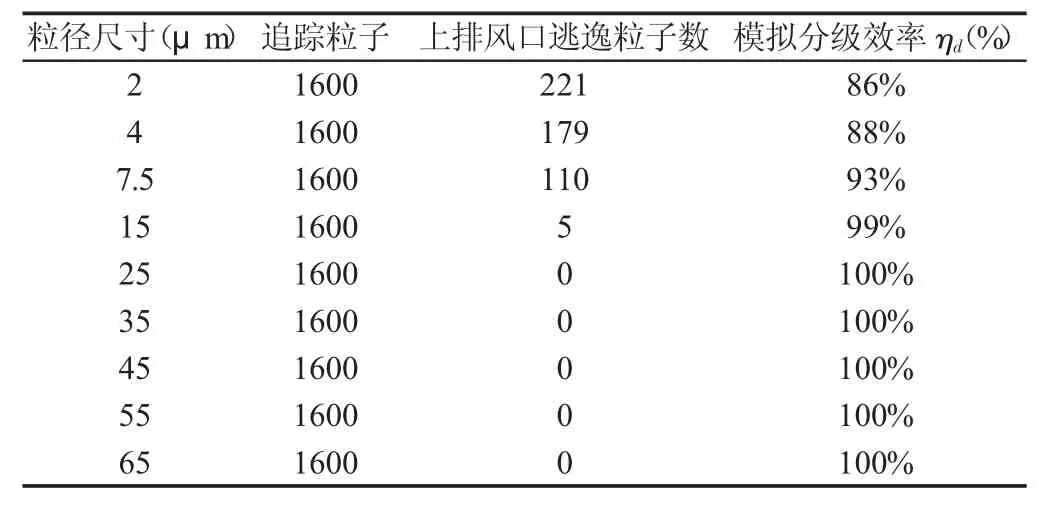
表3 各粒徑分級效率數值模擬結果Tab.3 Numerical Simulation Results of Particle Size Fractional Efficiency

根據式（10）可以求得數值模擬計算的總除塵效率的η=98.1%，與理論計算結果97.1%相比，相對誤差為：

相對誤差為1.03%，滿足誤差允許范圍[12-13]，說明數值模擬計算結果與理論計算結果吻合較好，表明設計的優化設計方案是可行的。

5 結論

（1）結合各結構參數對旋風除塵器進行除塵效率數學模型建立，當筒體直徑為328.0mm、總高度為1287.5mm、排氣管直徑為195.1mm、插入深度為246.2mm、入口高度為131.3mm、寬度為65.6mm、筒體高度為656.5mm時，總除塵效率最高，最大值為97.1%。

（2）計算旋風除塵器除塵效率時，不僅可以采用經驗公式選型設計，還可以借助CFD技術進行科學驗算，縮短設計周期，降低試制成本。