基于動態柔度極小目標的光電跟蹤設備拓撲優化方法研究

王強龍，謝軍，宮鵬，2，王曉明，劉震宇

（1.中國科學院長春光學精密機械與物理研究所，長春 130033；2.中國科學院大學，北京 100049）

光電經緯儀[1]設備用于跟蹤和測量動態目標的運動軌跡和運動姿態。車載、船載光電經緯儀需要結構部分輕量化、動態剛度好，尤其是在快速跟蹤測量過程中，需要結構的動態剛度足夠大[2]，光軸扭動足夠小。光電經緯儀在觀測狀況下引起結構振動的激勵來源是電機或旋轉伺服等周期載荷，而有限帶寬諧激勵下的響應峰值影響成像精度和穩定性[3-8]。因此，目標區域或指定點的動態柔度特性極小化設計是夠保證跟蹤系統跟蹤性能以及光學系統精度的重要手段。

本工作利用經典SIMP拓撲優化設計方法，以Du[3]等人定義的內積平方形式的動柔度目標作為基礎，提出多工況動柔度寬頻激勵優化模型并推導其敏度表達。通過定義多工況寬頻段激勵目標，利用動柔度設計的方法進行結構的優化設計。針對經典的立柱支撐結構，綜合參考結構負載和激勵目標頻段后對光學支撐找準架三維結構提出多工況優化設計方法；并對兩工況（靜載+扭轉動載）以及三工況（靜載+扭轉動載+晃動動載）下的優化模型及其優化算法進行數值驗證，獲得了多工況下動柔度極小的拓撲優化構型以及間接實現多特征值極大化優化方法，以期為同類負載下的結構設計提供參考。

1 基于動態柔度極小的多工況拓撲優化模型

1.1 基于SIMP方法的拓撲優化模型簡述

基于微結構和均勻化[4，9，10]方法擴展的 SIMP[5]（Solid Isotropic Microstructure/Material with Penal?ty）拓撲優化模型，通過帶懲罰項的材料相對設計變量ρ插值。結合濾波[6]等方法避免掉網格依賴、棋盤格等問題后，通過優化迭代將設計變量收斂到接近0或者1。本文所使用的單材料SIMP插值模型如下：

1.2 考慮工況的多頻（頻帶）動態柔度最小化拓撲優化模型

對于光電跟蹤設備而言，伺服控制頻率通常為某一頻率段的激勵頻率，有必要考慮在工況激勵頻率下，綜合分析結構動態響應特性頻率，對區段內動態柔度特征進行多目標極小分析。本文采用Du[3]定義的動態柔度模型，將外載荷幅值和載荷作用點處的結構位移的穩態響應幅值的乘積在整個作用域的積分作為優化目標。結構在多頻激勵下的動態柔度最小化問題實則為多目標優化問題，將各個頻率下的子目標寫成加權求和形式作為新目標進行優化。在指定的頻率區間內選定若干采樣點ωk∈[ ]ωl,ωh,k=1,…,Nω，分別計算各采樣點處的目標函數的頻響，最終的目標采用加權求和的形式表達。在目標頻率區間內的動態柔度最小化拓撲優化模型（忽略阻尼）如下：

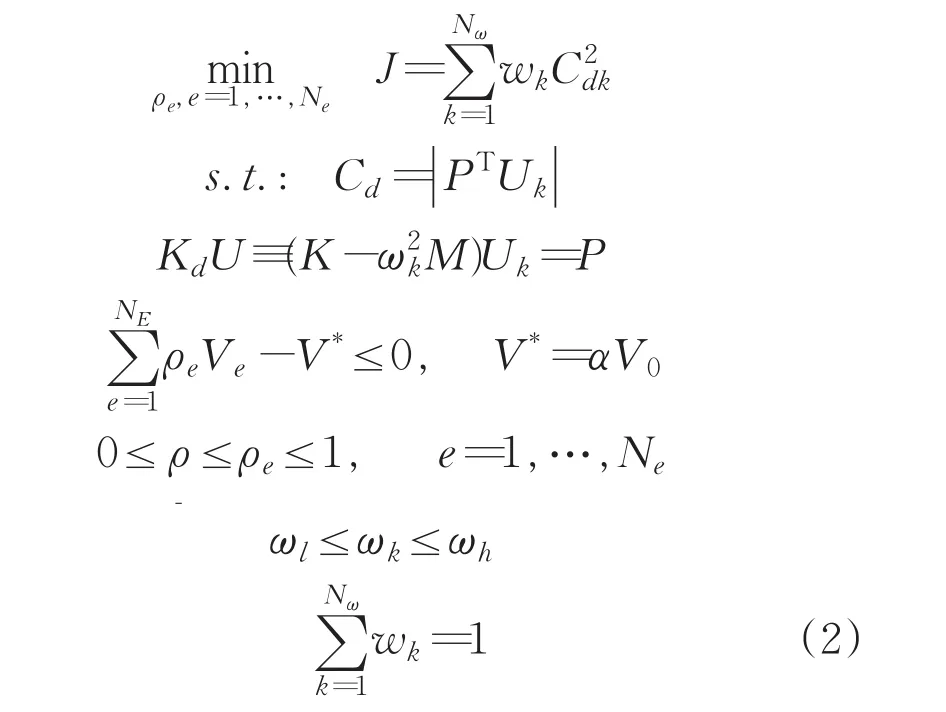
其中約束的第二式為結構穩態響應方程，ωk為給定簡諧變化的外載荷的圓頻率，wk為預先給定的與頻率ωk對應的權重系數。為動態剛度矩陣；ωk為給定簡諧變化的外載荷的圓頻率；外載荷表示形式為p(t)=Peiωkt，ωk∈[ωl，ωh]，k=1,…,Nω；對應穩態位移響應為x(t)=Ueiωkt。α為材料體積上限V*；相對于設計域體積V0的體積比。其中P和U分別代表有限元離散后的外載荷幅值向量和結構穩態位移響應向量幅值。考慮到多目標優化的復雜性，下文中暫取wk=1。ρe為設計變量。對應穩態位移響應為x(t)=Ukeiωkt ωk∈[ωl，ωh]，k=1,…,Nω。進行優化正問題求解時，進行掃頻步進諧響應分析從而得到待計算區段內最小柔度累加目標。敏度分析后對設計變量進行迭代更新。

1.3 多目標動態柔度最小化拓撲優化模型敏度分析

目標函數對拓撲設計變量ρe直接求導：

利用優化準則方法（OC）對優化模型進行迭代求解。

1.4 靜態柔度極小目標及敏度分析

靜載荷下的優化設計模型相當式（2）及式（3）中諧激勵頻率w＝0的情況，其優化模型和敏度表達式只需將ωk置零即可。

2 光電跟蹤設備找準架動態剛度極大化設計

光電經緯儀在其工作運轉時，光學主系統的轉動要求其支撐系統的動態剛度足夠大，否則將對跟蹤精度和成像質量產生明顯的影響。因垂直軸在跟蹤過程中系統激勵載荷為扭轉形式載荷，找準架（如圖1）承接光學設備和立柱，左右立柱的扭轉剛度同時影響伺服系統和光學成像質量。因此找準架在伺服激勵輸入下的動態剛度極大十分重要。

圖1 經緯儀結構以及找準架設計域和載荷工況示意圖

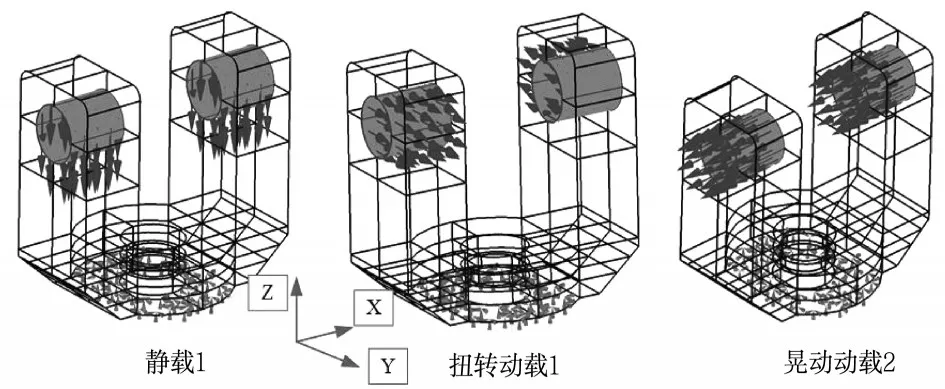
圖2 載荷工況視圖和約束視圖

2.1 找準架的跟蹤優化模型和負載設計

找準架計算模型如圖1所示，網格模型中單元總數為136224個，全部采用正六面體網格劃分左右立柱在X和Y方向上的一階動態彎曲動剛度影響中間四通的跟蹤穩定性和精度，因此下面主要針對左右立柱進行設計優化。經緯儀在跟蹤中，沿X方向和Y方向中的晃動對于跟蹤精度影響最大，四通和鏡筒在跟蹤找準架下以等效加速度的形式作用于垂直軸上。如圖2所示為半周期載荷作用的工況，載荷加載于軸承座上。其中，支撐靜載荷為立柱負載載荷，扭轉動載荷為Y方向左右扭轉載荷，晃動動載荷為X方向彎曲載荷。三個工況都約束底部邊界進行計算。計算正問題時，針對半周期下結果進行計算，之后將解對稱求解即可得。

2.1.1 設計目標

在伺服激勵跟蹤狀態下，保證設備足夠的靜態剛度之后，需要在伺服激勵頻段內有足夠的剛度以穩定光軸。本文選取的初始設計域是在經典找準架基礎上提煉而來，根據以往的測試和伺服試驗，將Y方向也即扭轉動載Dynamic Load 1（DL1）的優化頻段選取為50～60Hz，將X方向也即晃動動載Dy?namic Load2（DL2）的激勵頻段選取為20～30Hz。另外，為考慮到設計完整性，經緯儀結構的主要承載目標特性也需要考慮在內，也即添加Static Load1靜載，一并進行優化設計。

在靜載荷Static Load1作用下，設計目標為JST1；在DL1也即扭轉動載作用下，設計目標為JDL1：50-60Hz。在晃動動載DL2動載作用下，優化目標為JDL2：20-30Hz。有鑒于找準架在扭轉載荷下影響更為明顯，下面將對如下兩個多工況算例進行優化設計：

兩工況：靜載（ST1）+扭轉動載（DL1）

其中，α1和β1為目標權重配比系數，為使得計算目標在總目標中權重量級匹配，后文中取α1=100，β1=1。

三工況：靜載（ST1）+扭轉動載（DL1）+晃動動載（DL1）

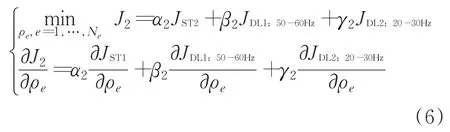
其中，α2、β2和γ2為目標權重配比系數，為使得計算目標在總目標中權重量級匹配，下文計算中取α2=100，β2=γ2=1。

2.1.2 初始設計目標的選取

動剛度優化和靜載荷優化所不同，存在目標參數非正定的情況。另外，初值區間和優化路徑嚴重影響優化的結果[7]。而本文的優化目標在于，在圖1的初始設計域內找出目標區間內扭轉動態剛度極大和晃動動載剛度極大的設計。有鑒于全填充設計域內扭轉剛度已經很高，將全填充的設計域作為初始設計變量顯然并不可取。因此，本文借助于SIMP插值方法找尋初始設計點。

Step1：分析全填充情況下圖1中Point A點頻響，此時在 SIMP 插值模型中，ρe=1,p=1，計算頻響曲線。

Step2：扭轉載荷下，頻響曲線峰值點若不在設計目標頻段內，改變SIMP插值參數。直到找到合適的插值初始點為止。

設計變量改變時，A點頻響函數曲線如圖3所示。

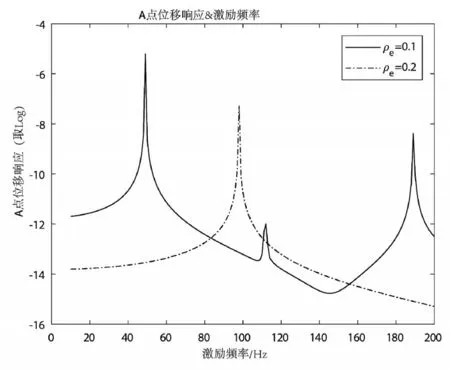
圖3 ρe=0.1，p=3；ρe=0.2，p=3點A頻響曲線

設計變量不同時，A點頻響函數曲線借助以上設計思路，在初值為ρe=0.1，p=3情況下，初設設計域共振頻率見表1所示。其中，與DL1載荷非正交的第1、2、5、6、7、8階模態可能影響結構在目標頻段的動柔度設計，與DL2載荷方向非正交的第3、4、5、6階模態可能影響結構在目標頻段的動柔度設計。

表1 ρe=0.1，p=3各階共振頻率

2.2 找準架優化動載荷下優化分析結果討論

2.2.1 兩工況優化算例結果

靜載荷ST1和扭轉動載荷DL1作用，在體積分數約束為Vol=0.1情況下，優化結果如圖4和圖5所示。優化設計后結構在動載荷DL1作用下Point A頻響曲線如圖6所示。從圖4和圖5的ZY投影視圖可以看出，當體積分數為Vol=0.1時，優化結果和二維梁結構基頻極大化設計結果類似[8]，在YZ投影方向呈現X形結構，且僅在另外一個維度上做平移拓展。而當體積分數Vol=0.2時，優化設計結果雖然在ZY投影方向上仍舊和小體積分數下的結果類似，但在另外一個維度上則有所差別。對比圖4（b）和圖5（b）可以看出，在兩工況下最終優化拓撲并未明顯受到體積分數的影響，也就是在扭轉諧激勵下的優化計算呈現保拓撲特性。

圖4 靜載+扭轉動載優化結果Vol=0.1

圖5 靜載+扭轉動載優化結果Vol=0.2

圖6的優化后頻響曲線表明，在扭轉動激勵載荷（Dynamic Load 1，Y方向）載荷作用下，結構在此方向的共振頻率趨向于遠離激勵頻段以降低響應幅值。從圖6中可以看出，在100～200Hz之間有較小的峰值，此峰值為軸承孔部位局部模態導致。而當體積分數變為Vol=0.2時，相對應的峰值則上升到300Hz左右。

圖6 靜載+扭轉動載優化后頻響曲線Vol=0.1&Vol=0.2

2.2.2 三工況優化算例

在靜載荷ST1、扭轉動載DL1以及晃動動載DL2三工況作用下，優化結果如圖7（體積分數Vol=0.1）和圖8（體積分數Vol=0.2）所示。圖7（c）為ZY方向投影視圖。Vol=0.1時，三工況優化結果和兩工況結果類似，以立柱加十字叉形式為主。在另外一個方向上圖7（b）中，由于晃動動載Dynamic Load 2諧激勵作用下正方向和反方向在立柱和回轉圓盤連接處的剛度不一致，導致優化出的結構并未呈現對稱X形。

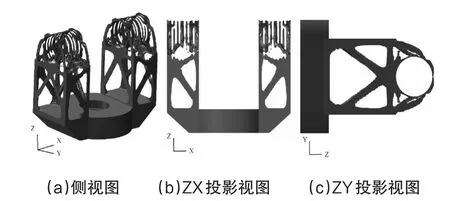
圖7 三工況（靜載+扭轉動載+晃動動載）優化結果Vol=0.1

圖8 三工況（靜載+扭轉動載+晃動動載）優化結果Vol=0.2

在體積分數Vol=0.2時，設計材料更傾向于分布在結構內側立柱，而最終呈現的拓撲構型則和Vol=0.1時類似。圖9是體積分數Vol=0.1時，經過優化設計后結構在扭轉動載Dynamic Load1和晃動動載Dynamic Load2作用下的點A頻響曲線。圖10是體積分數Vol=0.2優化設計后，結構在扭轉動載Dynamic Load1和晃動動載Dynamic Load2諧激勵載荷作用下的頻響曲線。Vol=0.2時，優化設計后的結構無論時在扭轉動載DL1載荷作用方向上，還是在晃動動載DL2載荷作用方向上，共振頻率都要高于Vol=0.1激勵下的設計結果。對比圖10和圖6，增加工況下，在扭轉方向（DL1載荷作用方向）共振頻率要稍低一些以滿足另外一個工況下的設計。

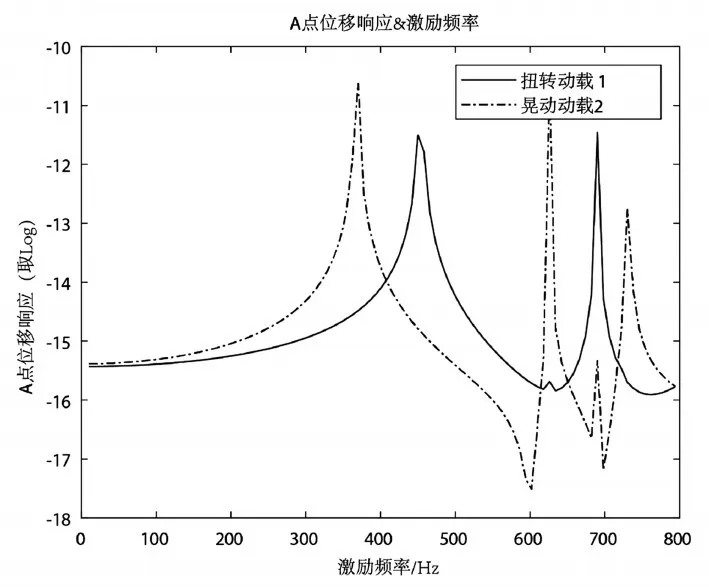
圖9 三工況優化設計后頻響曲線Vol=0.1，扭轉動載Dynamic Load 1載荷作用下A點頻響&晃動動載Dynamic Load 2載荷作用下A點頻響

從表2中對比兩工況和三工況下的頻率可知，在加入X方向晃動動載DL2諧激勵后，X方向一階彎曲基頻相較于兩工況結果有所提升，而在Y方向則有所降低。更多工況下呈現的結果以平衡各階響應幅值為主。

表2 優化設計后體積分數Vol=0.2的結構前八階共振頻率

3 結語

本文給出了利用SIMP拓撲優化方法，以動柔度平方形式作為目標進行的多工況寬頻段三維結構拓撲優化模型。目標頻段的動柔度極小設計思路可用于諧激勵下結構響應幅值極小化的設計，結構在激勵頻段下的極小化也意味著振動噪聲的降低以及系統穩定性和控制精度的提升。加入靜載工況后，拓撲優化呈現的結構接近于設備實際工作狀態。針對光電經緯儀找準架結構的拓撲優化結果表明此方法有如下特點：

（1）多目標特性下的動柔度極小拓撲優化能夠降低特定點的頻響峰值，從而保證在指定諧激勵下的響應量級極小。

（2）動柔度極小拓撲優化使得結構基頻遠離特定伺服頻率，最終呈現的優化結果和基頻極大化設計結果類似。

利用多工況動柔度極小作為目標進行結構拓撲優化，在合適的激勵頻率以及適當的非正交諧激勵載荷下，此方法給出的拓撲構型在滿足在動柔度極小的情況下能間接實現多個特征頻率極大化設計，無需考慮重頻以及模態交換等對于優化過程的干擾。相較于單一基頻極大化設計方法，對于工程設計有很好的應用參考價值。