基于貝葉斯推論的大壩潰口參數預測研究

2018-08-31 04:41:04趙敏，孫勇

水利科技與經濟 2018年1期

關鍵詞：模型

趙敏，孫勇

(貴州大學喀斯特環境與地質災害重點實驗室，貴陽 550002)

1 概述

大壩是極其重要的基礎設施，是綜合防洪工程體系和水力發電工程的重要組成部分，往往規模較大，其價值體現在防洪、發電、灌溉、航運、旅游、水產養殖等多個方面[1]。然而，一旦大壩發生潰決，不僅會造成社會經濟損失，更者會導致人員傷亡、生態環境問題等。國內外潰壩事故均有發生，我國1975年的板橋事件造成河南省29個縣市、1 100萬人受災，2.6萬人死亡，直接經濟損失近百億元[2]。1979年印度曼朱二號水庫潰壩事件，造成5 000～10 000人的死亡，經濟損失巨大。

大壩潰口形成過程和泄洪過程線(可細分為潰口特征參數、水庫蓄水量和下泄流量)的分析對已發洪水的危害評估至關重要[3]。分析大壩破壞以及泄洪水位線有許多模型，其中DAMBRK和HEC-1應用較廣，Singh和Snorrason采用這兩個模型對20個潰壩案例進行了關鍵潰口參數的敏感度研究[4]。Petrascheck和Sydler提出了一個數學模型來模擬洪水的外泄過程，研究潰口泄量、洪水位和洪水抵達時間對潰口寬度及潰口形成時間的變化的敏感度。該研究表明，可靠的估計大壩附近及下游區域洪水情況，準確地預測潰口參數是必要的[5]。

對潰口參數的評估有多種方式，Wahl總結為3種：類比法、基于物理原理的模型和預測方程[6]。類比法的前提是大壩間具有相似的幾何和水文情況；基于物理原理的模型運用水文學、泥沙運動學模擬潰決過程，往往因為缺乏對潰決機理的了解而過于簡化；而預測方程法在今天依然使用最為廣泛。預測方程參數一般是通過使用數據庫中對有限實例數據回歸分析所得最小擬合誤差作為唯一指標來得到的，而過度擬合常常導致公式十分復雜并影響預測方程的準確性。

本文運用貝葉斯推論的方法，對ICOLD統計的101個案例數據進行分析，選擇最優模型，從而提出可以平衡擬合能力和復雜性的預測方程。

2 潰口參數

潰口參數包括潰口的幾何參數、形成時間參數和水文參數。將潰壩理想化為一個不規則四邊形，見圖1。幾何參數即包括潰口深度(潰口高度)Hb(即壩頂至潰口反彎點的距離)、潰口頂部寬度Bt、潰口底部寬度Bb、潰口平均寬度Bave、潰口側坡因子Z。只要知道其中的任意3個參數就足以描述完整潰口的幾何情況。

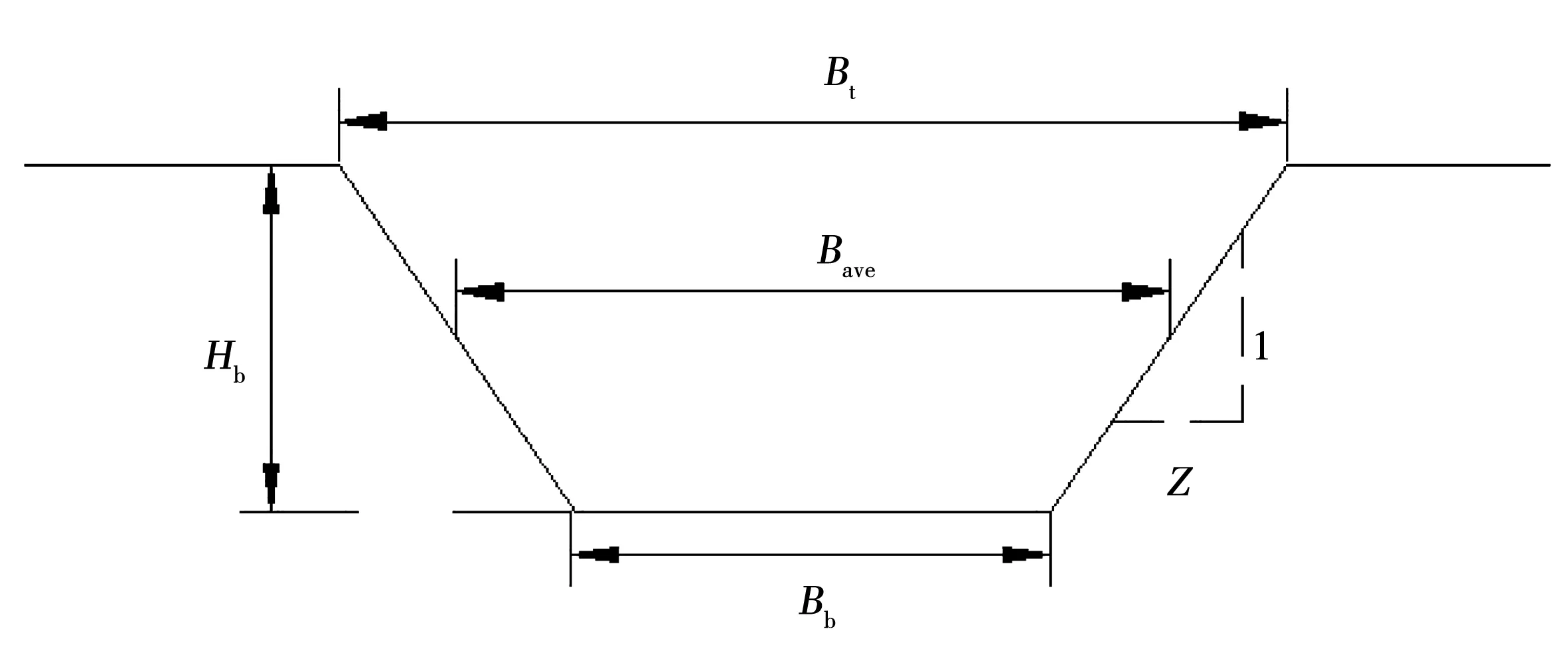
圖1 理想化大壩潰口參數圖

潰決時間Tf，Singh和Snorrason定義其為潰裂開始到完成的持續時間[4]。潰口開始時間起始于水流首次流過大壩，此時流出水量較小，隨著出流量和侵蝕迅速增加，潰口形成，潰口開始時間終止。潰口形成時間指大壩上游面首次潰決到潰口完全形成的時間。兩個參數較難區分。洪峰泄量Qp，取決于水庫的水位記錄或對側坡的測量。

基于潰壩的破壞機理，本文中涉及的參數只有4個：大壩寬度Hd、潰口水頭Hw(潰口深度Hb)、大壩水庫的容積Vd、潰口容積Vw。

3 預測方程參數和模型選擇

預測方程可以有加的形式和積的形式。

考慮到測量誤差的存在，輸出值以預測值和誤差項的總和的形式：

(1)

(2)

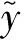
積的形式：

(3)

為了更方便地進行回歸分析，對式(3)兩邊取對數從而轉化為加的形式：

lny=β0lnx0+β1lnx1+…+βNxlnxNx

(4)

近10年來，貝葉斯推論被逐漸廣泛運用在工程中。為避免過度擬合導致公式過于復雜和影響預測方程的準確性，Yan等人提出了基于貝葉斯推論的模型選擇框架[7]。該方法有助于在一系列候選模型中挑選出一個具有最合理的輸入輸出關系的模型。貝葉斯模型選擇框架與現有的預測方程參數只考慮最小擬合誤差不同，旨在通過衡量擬合準確度(goodness-of-fit)和魯棒性(robustness)兩者，從而挑選出最合適的模型。模型合理性按下式計算：

j=1,2,…,NM

(5)

(6)

(7)

(8)

(9)

式(7)p(D|Mj,U)在實際計算中，經常用拉普拉斯的漸進展開來近似計算：

(10)

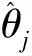
奧克漢因子被用于評估模型Mj魯棒性，如果模型參數對測量值很敏感并非是好事，這意味著擬合系數一個小的變化就會引起預測值出現一個對應的很大的改變。一個模型的奧克漢因子越高，魯棒性就越大，模型就越強健，對測量誤差的敏感度就越低[8]。

(11)

(12)

(13)

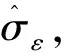
(14)

預測方程的廣義公式可以寫成如下形式：

(15)

式中：yi為向量y=[Hb,Bt,Bave,Qp,Tf]預測的破壞參數；xj為向量x=[Hd,Hw,Vd,Vw]中控制變量的選擇；Pi為模型Mj控制變量的集合。

4個潰口參數通過排列組合形成15個模型種類(表1)。

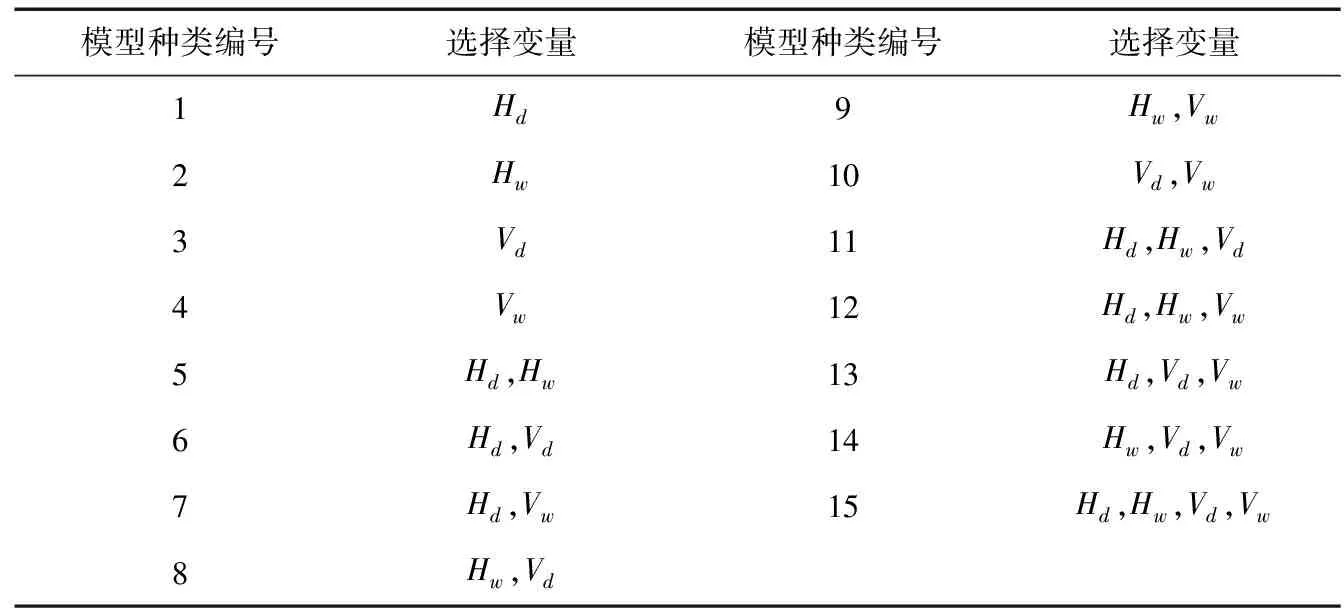
表1 模型種類列表

4 數據分析

4.1 控制變量與潰口參數的關系研究

見表2。

從表2可以看出，Bave與Hw有較大的相關性(ρ=0.61)，與Vd和Vw次之(ρ大于0.5)，說明潰口的平均寬度與潰口水頭的關系較大。同時，潰口水頭Hw相比較其他3個參數，潰口頂部寬度Bt與其相關性最大(ρ=0.65)；Hb與Hd(ρ=0.92)和Hw(ρ=0.97)都有很大相關性，說明潰口深度與大壩寬度和潰口水頭有密切關系；洪峰泄量Qp則是與潰口水頭Hw和潰口容積Vw有相對較大且相同的相關性(ρ=0.66)；對于潰決時間Tf而言，大壩水庫容積Vd和潰口容積Vw與其相關性較大(ρ=0.51)。

表2 相關系數表

4個控制變量與潰口參數之間的關系亦可通過散點圖得出。圖2以Hb為例，Vd、Vw、Hd、Hw的數據進行了標準化處理。

圖2中可以看出，Hd和Hw與Hb呈明顯的正相關關系，同樣驗證了潰口深度與大壩寬度和潰口水頭有密切關系。

4.2 模型選擇

每個候選模型的合理性和奧克漢因子值都可以通過基于貝葉斯推論的模型選擇框架獲得。圖3為Hb加的形式下的預測結果。圖3中同時包含只代表模型準確度的大小的確定系數R2和奧克漢因子的對數形式，以便做出比較。

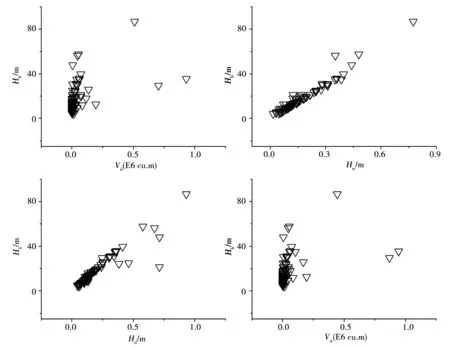
圖2 潰口深度Hb與各變量關系圖

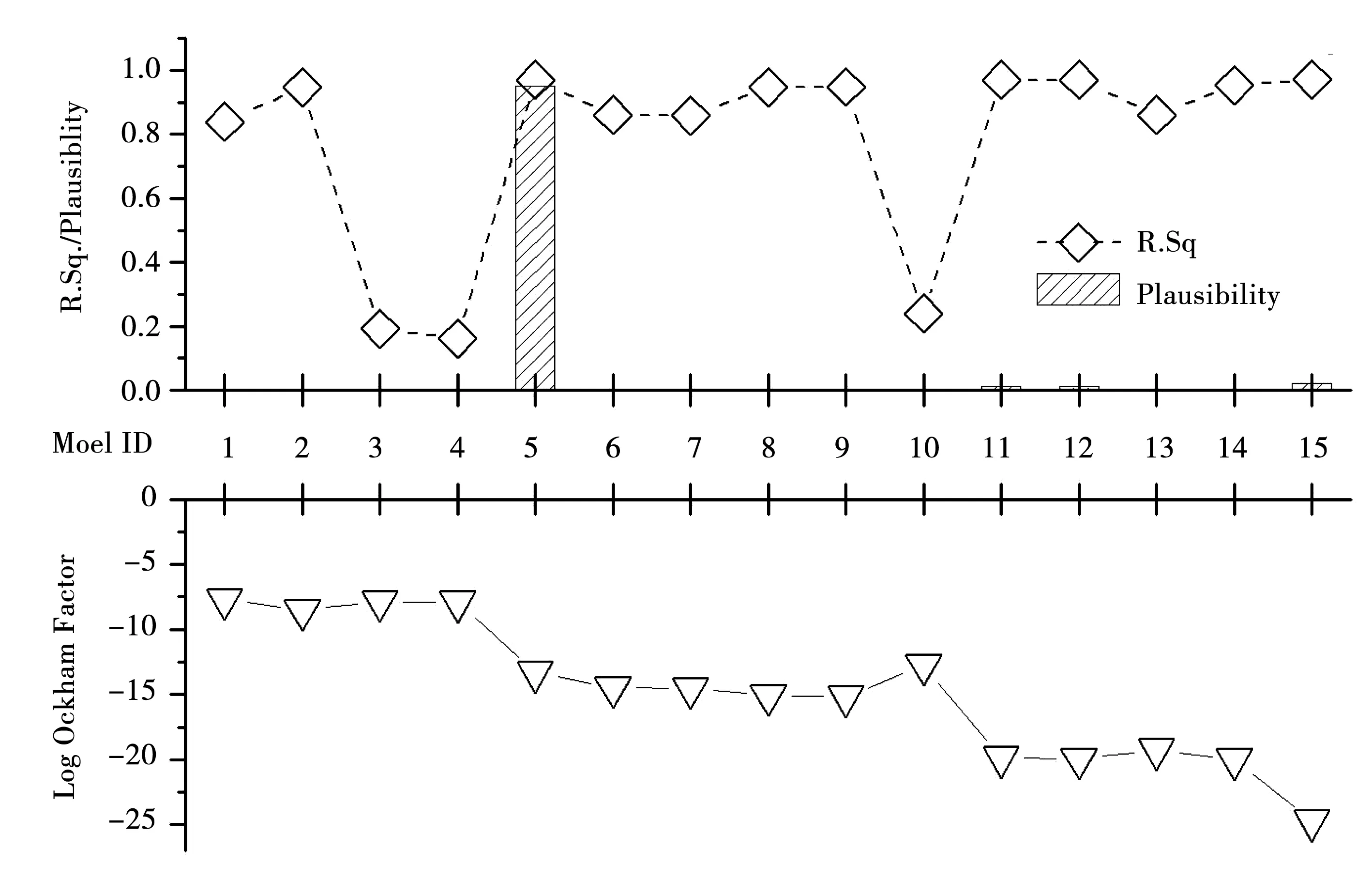
圖3 Hb的模型分析圖

從圖3中可以看出，模型15具有最大的R2值。然而模型15的奧克漢因子對數值最低，這表明雖然該模型有很高的準確性，擬合誤差最小，但是魯棒性最低。也就是說，模型15對測量值的變化很敏感，不利于預測。模型5不僅有最大R2值，而且奧克漢因子對數值較小，可以作為最優的模型選擇。同理，可以找出其他潰口參數的最優模型。

潰口參數相關性最大的變量和最優模型的R2值的關系見表3。從表3中可以看出，具有最大準確度，即R2值最大的模型并不是最理想的。

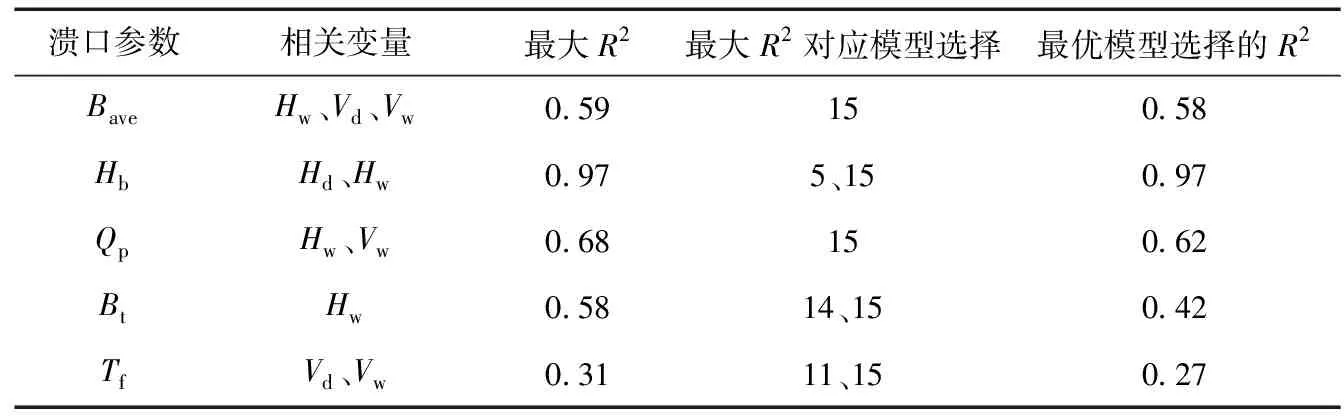
表3 R2值與相關變量關系

5 結論

貝葉斯推論近10年在工程中的應用比較廣泛，也體現出其優越性。預測方程參數通常使用最小擬合誤差作為唯一指標，模型選擇過程中只考慮準確度，過度擬合不僅使公式過度復雜，也會導致預測結果不理想。本文運用貝葉斯推論分析了水壩潰口參數與變量之間的關系，驗證了模型選擇時不能只考慮準確度，導致過度擬合，還應該考慮模型的魯棒性，最后根據最優模型得出的預測方程對測量值變化較不敏感，更具有可預測性。