基于改進的Lee-Fenves模型的混凝土堆石壩抗塑性損傷數值分析
汪海龍
(大石橋市水利工程移民局,遼寧 大石橋 115100)
0 引 言
近年來,混凝土堆石壩以氣候適應性強、造價經濟的特點,在國內許多地區中小水利工程中得到應用[1-5]。混凝土堆石壩的安全性一直是國內外學者研究的首要問題。在工程設計時需要對混凝土堆石壩的塑性損傷進行分析。目前,在國內混凝土堆石壩抗震數值分析較多的是Lee-Fenves 模型[6-10],該模型具有較強理論分析基礎。但傳統Lee-Fenves 模型在進行水工建筑物抗拉計算時,不可實現混凝土鋼體抗拉動態計算,存在一定的局限。有學者引入抗拉應變曲線,實現了對傳統Lee-Fenves 模型的改進,但是改進的Lee-Fenves 模型在混凝土堆石壩抗震能力分析的應用還不多見。為此,本文引入改進的Lee-Fenves 模型,以遼寧南部某混凝土堆石壩為工程實例,對該混凝土堆石壩的塑性損傷進行數值分析,并結合原型觀測試驗分析改進的Lee-Fenves 模型在應力計算的精度上的改善。
1 改進的Lee-Fenves 模型原理
傳統Lee-Fenves 模型基于混凝土塑性原理進行應力的計算,計算方程為:
(1)

在應力計算的基礎上,結合剛性屈服和流動準則計算混凝土剛性屈服度,計算方程為:
(2)
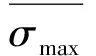
傳統Lee-Fenves模型采用流動方法計算塑性應變,計算方程為:
(3)
其中:
(4)
式(3)和式(4)中:λ為塑性不變量;ap為與混凝土強度相關參數。
此外,方程還對混凝土堆石壩塑性損傷的損傷計算分析,計算方程為:
(5)
式(5)中:σg為不用應力下的應力狀態變化曲線。在不同應力狀態下的混凝土堆石壩抗震強度計算方程為:
(6)
式(6)中:ag為抗震強度參數。
改進的Lee-Fenves模型在傳統Lee-Fenves模型模型基礎上,對應力變化曲線進行改進,提出混凝土抗拉變化曲線計算方程:
(7)
其中:
(8)
式(7)和式(8)中:Y為應力比值;f為抗拉強度系數;X為應變比;af為混凝土鋼纖抗拉曲線系數;lf為鋼體長度;df為鋼體直徑;pf為鋼纖抗拉體積。
改進Lee-Fenves模型的混凝土塑性損傷計算方程為:
σ=f(εp)
(9)
其中:
εp=ε-σ/E
(10)
式(9)和式(10)中:σ為應力。
2 模型應用
2.1 工程實例
本文以遼寧南部某混凝土堆石壩為研究實例,結合改進的Lee-Fenves 模型分析混凝土的塑性損傷,結合應力觀測試驗分析模型在混凝土堆石壩的適用性。模型原型觀測試驗應力監測點布置及有限元三角網格分布見圖1。混凝土堆石壩材料主要彈性模量為200 GPa,混凝土鋼體屈服度為400 MPa,混凝土堆石壩主要計算特性參數見表1。
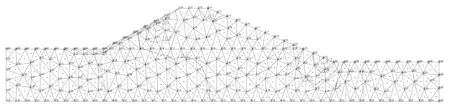
圖1 工程實例混凝土堆石壩應力監測及計算有限單元格Figure 1 Engineering Example Concrete CFRD for stress monitoring and calculation of finite cells

αβ/GPaλαpD/MPaαg1.502.352003503.504004.50
2.2 模型驗證
抗拉性是反映混凝土土石壩塑性損傷的主要特性指標,結合原型觀測試驗對改進前后的Lee-Fenves 模型對混凝土的抗拉強度進行驗證和對比,計算結果見表2。

表2 模型抗拉強度計算結果對比Table 2 Comparison of model tensile strength calculation results
從表2中可以看出,改進的Lee-Fenves模型在混凝土堆石壩抗拉強度計算值和試驗值之間的誤差為7.1%~11.7%,而傳統的Lee-Fenves模型計算的抗拉強度計算值和試驗值之間的誤差為15.4%~29.2%。這主要是改進的的Lee-Fenves模型采用抗拉曲線,實現了混凝土鋼體抗拉應力的動態計算,提高了模型在混凝土堆石壩抗拉的計算精度。
2.3 不同強度下的混凝土堆石壩塑性損傷試驗分析
為合理設置改進的Lee-Fenves模型的計算參數,采用原型觀測試驗方式,對不同參數下的混凝土堆石壩的塑性損傷進行試驗分析,各參數下的試驗分析結果見圖2。
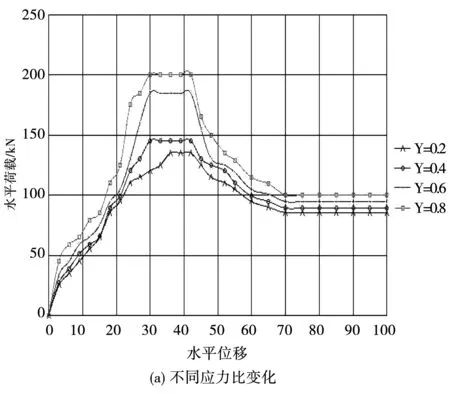
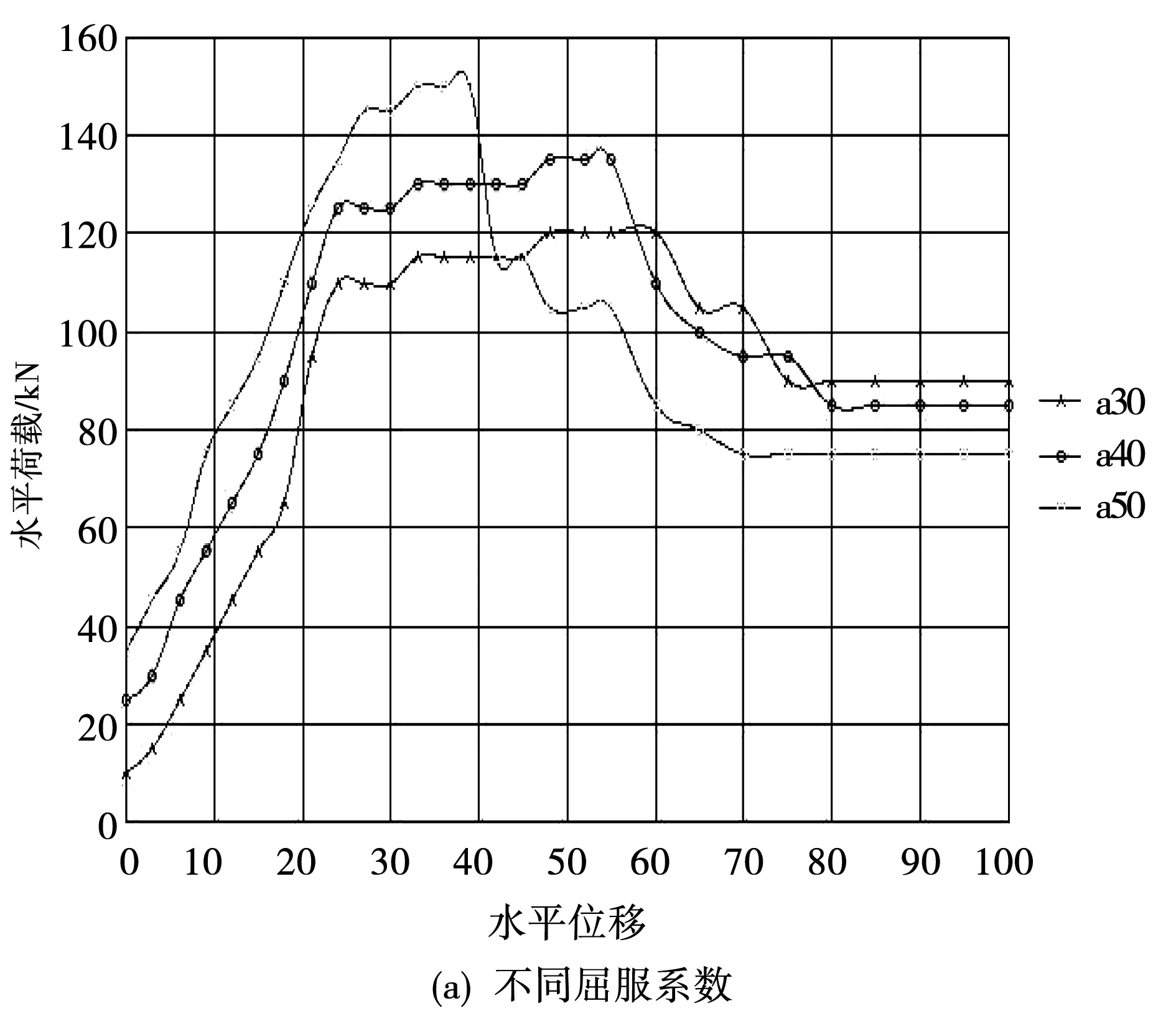
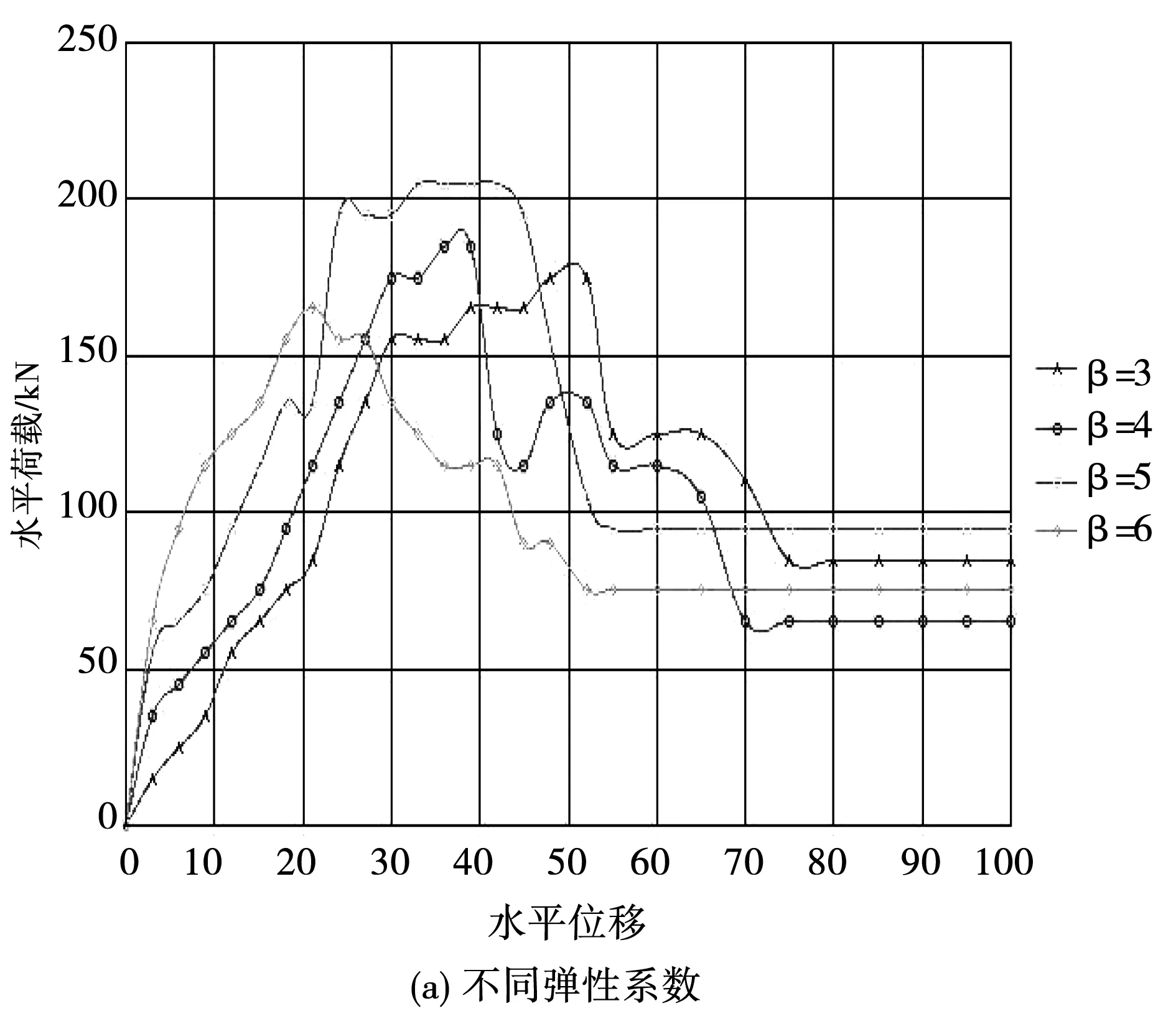
從圖2中可以看出,不同應力參數下混凝土堆石壩的位移和水平荷載變化曲線具有各異性。從不同應力變化下的位移和荷載變化曲線可以看出,應力比對混凝土堆石壩的彈性強度影響較小,應力比較大,混凝土應力荷載逐步增加,荷載位移逐步上移。從不同屈服系數下的位移荷載變化曲線可以看出,當水平位移在35 mm前,隨著屈服系數的增加,荷載逐漸增加;當水平位移達到35~40 mm后,隨著屈服系數的增加,其荷載逐步較小,但幅度較為緩慢。從不同彈性系數下混凝土堆石壩位移荷載變化曲線可以看出,隨著彈性系數增加,其位移荷載變化較為不同,其變化臨界點主要出現在水平位移在25~35 mm之間。抗拉強度是反映混凝土堆石壩的一個重要特征指標,從不同抗拉系數的水平荷載和位移曲線可以看出,隨著抗拉系數增加,其位移和水平荷載逐步增加,但增加幅度較小。
2.4 混凝土堆石壩面板塑性損傷分析
混凝土堆石壩面板厚度很大程度決定了混凝土堆石壩塑性損傷,為此結合改進的Lee-Fenves模型對不同面板厚度下的塑性損傷進行數值模擬,模擬結果見圖3。

圖3 不同面板厚度下的混凝土堆石壩面板塑性損傷模擬結果Figure 3 Plastic damage simulation of concrete faced rockfill dam with different panel thickness
從圖3中可以看出,隨著面板厚度的增加,其面板塑性損傷的范圍逐步較小,面板厚度增加對混凝土堆石壩塑性損傷影響較為明顯。從不同厚度面板塑性損傷的范圍可以看出,當H=200 mm時,其塑性損傷主要發生在中下部區域;當H=300 mm時,其塑性損傷的區域和面板厚度為200 mm較為相似。可見,面板厚度在200~300 mm之間,對混凝土堆石壩塑性損傷影響較弱;當混凝土堆石壩面板厚度達到400 mm時,可以看出面板抗震塑性損傷大幅度減小。當面板厚度增加到500 mm時,可以看出面板塑性損傷明顯降低。從不同面板厚度的抗震塑性分析可看出,當混凝土鋼體厚度從200 mm增加至500 mm時,強度增加25%,損傷面積減少30%。在易損區域,應該增加混凝土鋼體的厚度,降低混凝土堆石壩的塑性損傷。
3 結 論
1) 改進的Lee-Fenves模型抗拉曲線,解決了傳統Lee-Fenves模型不可實現抗拉應力的動態計算的問題,提高了Lee-Fenves模型在水工建筑物抗拉應力分析中的精度。
2) 應力比對混凝土堆石壩塑性損傷影響較大,在應用改進的Lee-Fenves模型計算其抗震穩定時,應重點關注應力比這項參數。
3) 面板厚度增加,塑性損傷范圍逐步減小。在易損區域,應當增加面板中鋼體的厚度,減小混凝土堆石壩的塑性損傷。

