磨粒有序化砂輪磨削規則表面的仿真研究*

沈陽理工大學機械工程學院 沈陽 110159

1 研究背景

隨著現代科技的高速發展，規則表面逐漸成為國內外各種機構研究的熱點之一［1］。規則表面基于工程仿生學，將減阻、減摩、抗粘附和抗磨損等特性應用到實際生產加工中。現有的應用主要集中在改變零件表面幾何形態方面。目前，加工規則表面的方法有激光鐳射、化學蝕刻或壓刻技術等，采用這些方法能使零件表面具有一定尺寸和排列的坑、槽、凸包等非光滑形貌［2-5］。

現階段表面結構化砂輪研究很多，但對于利用表面結構化砂輪磨削規則表面進行研究還很少［6-7］。筆者通過對砂輪磨削運動過程的研究，建立磨粒運動軌跡模型，然后選擇合理的磨粒排布方式，建立磨粒排布方程，推導出磨削規則表面的約束方程，應用仿真軟件仿真磨削過程，對磨削的三維表面形貌進行分析，總結磨粒排布、磨削形貌及磨削用量的相互關系［8-9］。

2 運動軌跡模型

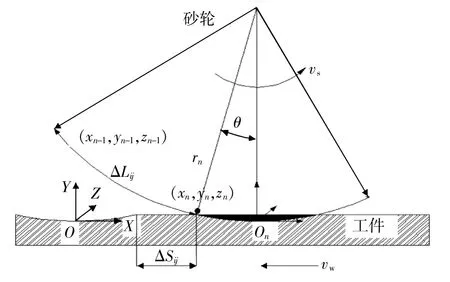
在研究磨削過程時，為了更好地進行分析，選擇先對單顆磨粒磨削過程進行研究，然后擴大到砂輪表面上任意一顆磨粒。當砂輪在進行磨削運動時，磨粒隨砂輪作旋轉運動，工件相對于砂輪進行平動，為了方便研究磨粒運動軌跡，建立單顆磨粒運動模型，如圖1所示，將坐標原點O（xyz）設置在接觸點上。

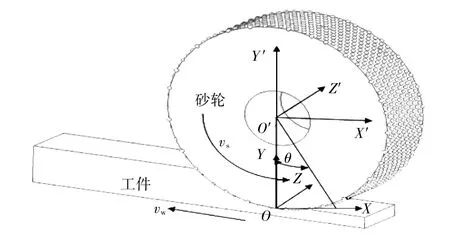
▲圖1 單顆磨粒運動模型

根據圖1，當砂輪在磨削過程中只作純滾動時，磨粒的頂點軌跡為延長外擺線。根據建立的模型可以推導出磨粒的運動軌跡，在任意時刻t單顆磨粒的運動軌跡為：

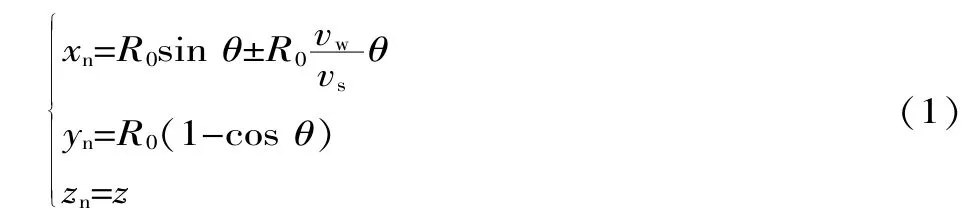
式中：R0為砂輪半徑；θ為砂輪在單位時間內轉過的角度；vs為砂輪線速度；vw為工件進給速度。

在單層磨粒排布砂輪的磨削過程中，假定砂輪表面的磨粒都將參與磨削，達到加工出規則形貌表面的目的，則磨粒排布必須為規則排列。為了對比不同排布方式的磨削特點，采用三種排布方式進行研究。磨粒主要排布方式有葉序、錯位和矩陣，如圖2所示。

基于文獻［10］葉序排布理論，磨粒會在砂輪表面呈螺旋上升排布，其排布方程為：

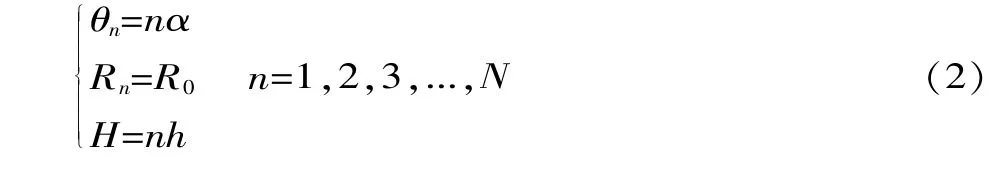
式中：（θn，Rn，H） 為葉序排布點在圓柱面中的坐標；n為磨粒在圓柱表面上的序數；α為葉序發散角；h為葉序生長因數。

對于錯位排布，結合相關資料進行研究，得出錯位排布砂輪的圓柱面坐標表達式為：

式中：i和j分別為磨粒所在的砂輪周向排列和軸向排列的行數；a為磨粒間距；I為周向磨粒總行數，I=2πR0/a；R為砂輪圓柱半徑。

根據對矩陣排布方式進行分析研究，可得出矩陣排布砂輪的圓柱面坐標表達式為：

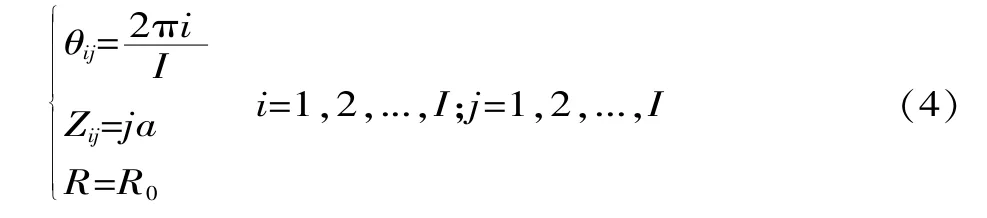
3 約束條件

在磨削運動過程中，工件進行平動，所以每個磨粒在進行切削時，在工件表面所形成的切削痕跡是不同的。工件表面所形成的兩顆磨粒縱向磨削痕跡由劃痕大小和磨削深度所共同決定，工件表面所形成的橫向劃痕間距則與砂輪線速度、工件進給速度和磨粒旋轉周期有關。

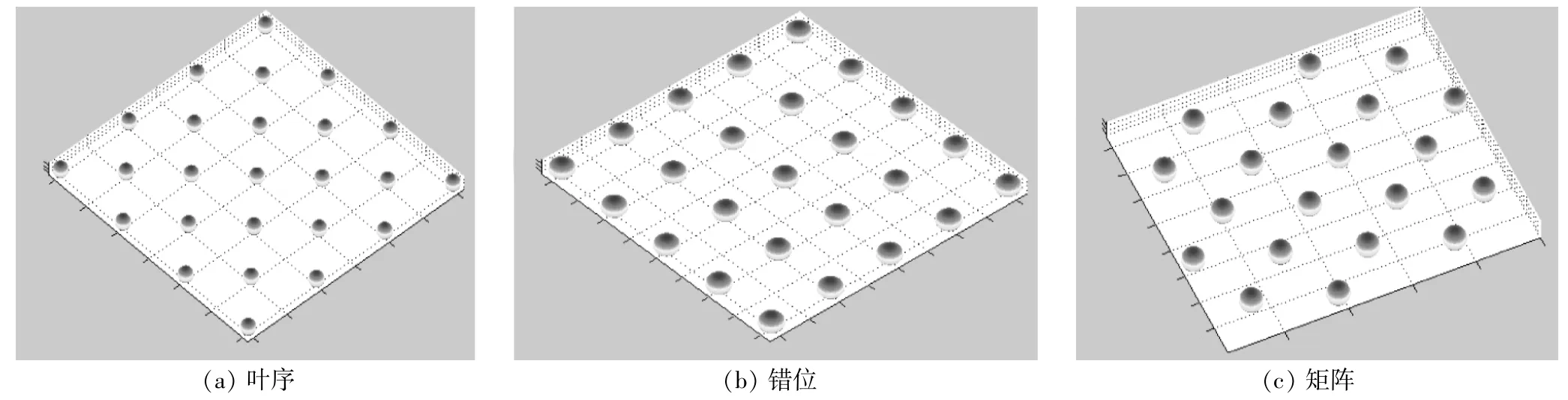
▲圖2 磨粒排布方式

相鄰磨粒磨削模型如圖3所示，假設兩顆磨粒在工件表面形成的劃痕間距為ΔSij，在相同的時間Δt內有：

式中：ΔLij為磨粒在磨削狀態下轉過的弧長；lij為砂輪上磨粒相對于初始點的弧長；n′為砂輪旋轉的圈數；ds為砂輪直徑。

設砂輪寬度為dg，在葉序排布中，砂輪表面的磨粒數N可表示為：

在任意Δt時間內，磨粒的橫向距離都可以表示為：

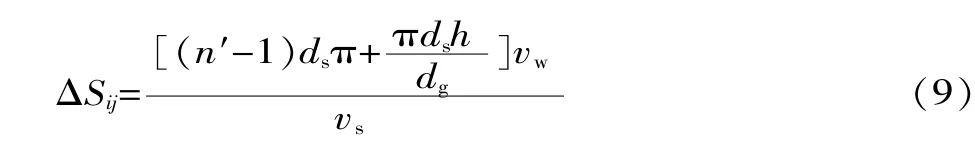
對于錯位和矩陣排布方式，主要是橫向公式不同，具體表達式為：

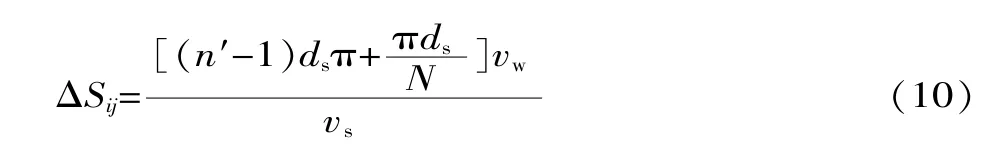
第1顆磨粒與第n顆磨粒的徑向距離Δr為兩顆磨粒的徑向坐標之差：

由上述分析，根據磨粒的排布方式及運動軌跡，可以得到任意一顆磨粒的軌跡方程為：

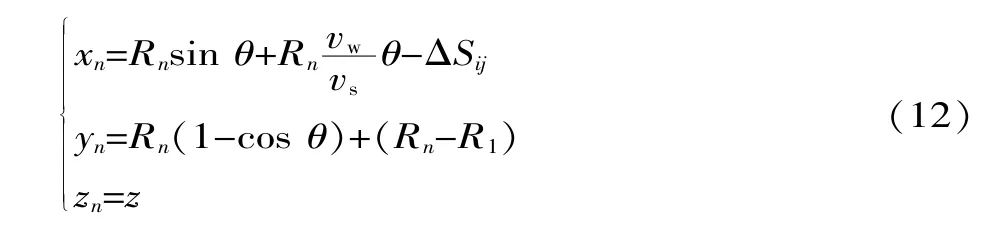
4 規則表面形貌仿真

在磨粒有序化砂輪磨削過程中，為達到規則表面的目的，磨粒排布稀疏，并且在加工時多采用較小切削深度和較大進給速度。應用MATLAB軟件對砂輪磨削運動進行仿真，在同一個砂輪線速度vs=1 836 mm/s的情況下，對于不同進給速度vw=800 mm/s和vw=1 200 mm/s，仿真出不同切削痕跡。砂輪直徑為100 mm，切削深度為20 μm，磨粒采用六邊形，仿真結果如圖4所示。

由圖4可以觀察到，在不同磨粒排布方式下，采用適當的磨削參數，可以仿真出相應的磨削工件表面三維形貌，實現規則表面的仿真磨削。

▲圖3 相鄰磨粒磨削模型

▲圖4 砂輪磨削仿真結果

5 結論

筆者采用磨削原理仿真磨粒有序化砂輪磨削規則表面，應用建立的磨削模型，推導出磨粒與工件的相互關系，應用MATLAB軟件進行仿真，分析磨粒排布參數對規則表面的影響情況，同時結合砂輪線速度和工件進給速度，總結規則表面的形成規律。

對仿真結果分析發現，采用磨粒有序化砂輪可以準確磨削出規則表面，直觀反映出磨粒作用在工件表面的情況。

選擇適當的排布參數和磨削用量，能夠磨削出凹坑和筋條表面。通過仿真研究，驗證了磨削模型的準確性，為后續試驗磨削規則表面提供了參考。