基于BP神經網絡的井下機電節能研究

張躍輝

(山西新村煤業有限公司,山西 長治 046000)

在井下機電設備中,以井下掘進機電氣設備耗電量為最大,此類設備中,大功耗電氣設備有電力變壓器、電動機、帶式輸送機和掘進機四種。而電力變壓器又是輸電網絡中的主要設備,是電力安全傳送的重要保障。隨著井下供電需求的增加,電力變壓器容量越來越大,其帶來的能量耗損問題也日益凸顯。電力變壓器的能量耗損主要是運行過程中的空載和負載,二者均可由試驗獲得。實際生產中,既要保證低空載損耗,還要降低負載損耗,這就要求統籌優化好兩者之間的比例。

20世紀70年代,奧地利學者計算變壓器電流時忽略了集膚效應,然后從其它方面提高了算法精度;隨后的德國科學家,在忽略集膚效應的基礎之上,又建立了變壓器中各個參數在不同頻率影響下轉換的數學模型,依次優化各個參數[1]。傳統的BP神經網絡中使用的是常數學習率,本文擬從均方誤差與權值的角度出發,每個迭代步產生誤差后都進行調整,即對各層的權值進行動態調節,此法亦稱為自適應步長法。具體來說就是用隨機選擇的歸一化樣本來訓練和預測方法，預測井下掘進機的電壓。當求得預測值與真實值間的誤差≤0.04,說明改進的方法有效。

2 神經網絡原理

2.1 神經網絡模型

人工神經網絡簡稱ANN網絡,是受動物神經網絡結構啟發,讓要實現的原理或功能自己進行模擬和訓練,即具備自學能力。人工神經網絡單元與單元之間由權值連結,神經網絡的好壞直接取決于權值[2]。選擇不同的權值,得到不同的神經網絡,其訓練效果也不同。神經網絡是由多個神經元組成,包括輸入層、中間層、輸出層,每個神經元在輸入數據后都能輸出單一的結果[3]。按照拓撲結構的分類原理,可將人工神經網絡分為前饋型和反饋型。后者應用范圍最廣,但是也要求較高的計算能力和反饋調節能力,結構也較前者復雜。神經網絡訓練方法,是每次迭代之后,權值都會根據記憶和自身優化能力進行調整。神經網絡的穩定輸出取決于網絡內部結構的權值和輸入數據。輸入數據的隨機性越大,誤差越大。反饋型神經網絡的缺點在于,網絡訓練的權值要朝著誤差遞減的方向進行訓練,在這種情況下會產生一種偽狀態(局部極小值),不能實現全局最優收斂。前饋型神經網絡中,權值處理方向都指向數據輸出方向,即方向單一。換言之,在神經網絡方法訓練過程中,各層神經元之間的權值是相互關聯的,表示輸入層和輸出層間的關系,沒有訓練的神經網絡,其權值就沒有意義,所以該網絡不能被用來預測數據[4],神經網絡權值系統圖見圖1。

圖1 神經網絡權值系統圖Fig.1 Weight system of neural network

本文擬選用前饋型神經網絡中的經典算法——BP神經網絡算法來預測電壓。利用其單向的訓練學習方法,可以將輸入的預測數據從此神經網絡中優化輸出。

圖1是神經網絡的一個典型模型——多入單出的非線性模型。n表示數據輸入個數，X表示系統輸入信號，W表示權矢量，f(·)是激活函數。具體步驟如下：①訓練樣本X被作為輸入信號輸入，通過調整權系數W，得到相應的結果，然后輸出；②把期望的數字信號當成訓練的信號，與①中結果進行比較，得到誤差；③用得到的誤差去控制和修改權系數W。如果將上圖輸出結果記為u的話，則有：

u=∑WiXi=W1X1+W2X2+…+WnXn.

(1)

式中，i=1,2,…，n表示樣本數。

用期望輸出信號Y(t)和u對比,得到誤差信號m,然后利用誤差m沿誤差減小的方向調整權值,直到滿足系統設定誤差。學習過程結束的標志是實際輸出值u和期望輸出值Y(t)無限逼近。

2.2 傳統BP神經網絡算法

傳統的BP神經網絡原理包含:向前傳輸數據,反向傳輸輸出值與樣本值間的誤差,動態修正權值。在傳統的三層BP網絡算法中,設輸入層、隱含層、輸出層分別含有神經元A、B、C個,對應的某一神經單元符號為xi、ym、zn。記xl到ym的權值為Wlm,ym到zn的權值為Wmn,設定傳遞函數,于是得到網絡結構圖,見圖2。

圖2 三層BP網絡Fig.2 Three-layer BP network

根據網絡順序,記輸入與輸出分別為u、v,系統輸出的表達式為:

(2)

式中：C為輸出結果C的向量。

期望函數為:

D(n)=[d1,d2,…,dC].

(3)

2.2.1工作信號正向傳播

輸入n個信號,輸入層輸出:

(4)

(5)

假設f(·)為sigmoid函數,則網絡隱含層的第i個神經元的輸出等于:

(6)

(7)

網絡輸出層第j個神經元的輸出為:

(8)

其相應的誤差為

(9)

整個網絡的總誤差可表示為:

(10)

2.2.2誤差信號反向傳播

1)調整隱含層與輸出層間的連接權值:

=ΔWbc(n)+Wbc(n) .

(11)

此時偏導可表示為:

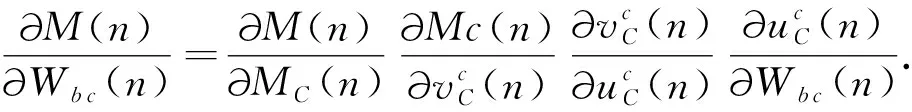
(12)

其中,

再將傳遞函數用其導數表示,可以得到梯度值如下式:

(13)

再經權值修正量修正后可得到局部梯度如下:

(14)

又因為神經元的局部梯度的傳遞函數通常是線性的,可知其導數為1。

2)誤差信號向前傳播,對輸入層與隱含層之間的權值Wab進行調整。與上一步類似,應有:

(15)

同樣的,有局部梯度為:

(16)

上式中,f(n)為sigmoid函數。由于隱含層不可見,因此無法直接求出誤差對該層輸出值的偏導,于是需要上一步計算中求得的輸出層節點的局部梯度:

(17)

故有:

(18)

至此,整個神經網絡訓練過程結束,簡言之，修正權值等于系η，局部梯度δ，輸出值υ的積，即：可將過程簡化表示如下:

ΔW=ηδv.

(19)

3 改進的BP神經網絡法

3.1 改進內容

傳統的BP神經網絡算法中,結果的收斂速度很大程度上取決于常量值學習率,即影響訓練時間和訓練結果。本文從學習率常數出發,將傳統的神經網絡學習率常數修改成自適應變化的學習率常數,即記錄每次迭代產生的均方誤差,及時調整學習率。改進算法為:

(20)

改進算法所對應的權值變化為:

(21)

改進后的神經網絡算法可以具體的描述為以下步驟:①選取樣本庫,設定網絡結構,初始化網絡權值和閾值,并且設定訓練誤差允許值ε；②輸入樣本；③輸出結果,計算各層輸出誤差,再通過訓練樣本求得樣本總體的誤差；④調整各層的權值；⑤迭代n+1次,分別向前和反向進行計算,直到誤差滿足設定的閾值,訓練結束。

3.2 改進后神經網絡應用

本文從煤礦實際情況出發,建立井下掘進機電壓的非線性模型,利用BP神經網絡建立配電系統中的電壓預測結構。具體分為以下步驟:

1)選擇和組織樣本數據。選取在區間[-30,30]上的電壓,擴大樣本容量,并對端口數據進行標準化處理。

2)建立網絡結構。建立三層BP網絡模型,設定網絡節點輸入數為10,網絡節點輸出數為3。根據Hecht-Nielsen理論[7],訓練過程中的隱含節點數等于2X+1(X為輸入節點數目)。于是,拓撲網絡結構就是10×21×3。采集10次數據,將結果作為10維向量輸入,輸出一個3維向量。

3)系統仿真。設定采樣周期為30ms;用二階慣性系統隨機選擇數據,并將數據歸一化處理;電壓標準值設定為220V,波動區間[-30,30];開始訓練和測試。具體的測試矢量限于篇幅不再列出,直接給出改進的訓練曲線見圖3,并將改進后曲線同改進前曲線做對比。

圖3 樣本曲線對比Fig.3 Comparison of sample curves

通過對比可以看出,預測曲線與實際曲線基本是吻合的,誤差最大處為0.04,可以接受。而且發現,傳統方法迭代需要234次達到的精度,改進后的迭代算法只需5次就能達到,極大地提升了運算效率。

4 結束語

本文推導了神經網絡的算法,闡明了傳統BP神經網絡在迭代和誤差精度上的不足之處。然后通過利用自適應步長法及時調整輸入層、隱含層、輸出層間的權值,擴大樣本容量,歸一化樣本;將改進的算法用于實踐,得到誤差較小的預測值。