基于結構優化技術的頂蓋結構設計方法研究

羅慧娟，蘇曉宇，付廣

(上汽通用五菱汽車股份有限公司技術中心，廣西柳州 545007)

0 引言

汽車頂蓋主要由頂蓋外板和頂蓋橫梁組成。頂蓋由于外板剛度較低，且具有較大的聲輻射面積，其固有頻率容易與車內空腔和發動機的二階振動耦合，激發車內噪聲。此外，頂蓋外板在日常使用過程中常會受到外載荷的作用，如人為的觸摸按壓、積雪的靜載荷及碎石沖擊等，使頂蓋發生外板凹陷及結構失穩等現象。因此，在設計時，需要兼顧模態、抗雪壓性及抗凹性的要求。

目前，對于單一性能的影響因素及性能提升方法研究已較深入，但各因素對模態、抗雪壓及抗凹性的影響卻存在相互制約的現象。例如：頂蓋外板加筋條在提升抗雪壓性及抗凹性的同時，卻降低了模態。在輕量化設計成為必然的大環境下，頂蓋的覆蓋件及橫梁已越來越薄。如何在兼顧輕量化同時，設計出滿足頂蓋模態、抗雪壓及抗凹性的頂蓋結構，成為困擾設計人員的問題。

結構優化技術是當前CAE(Computer Aided Engineering)技術發展的一個熱點，通過優化技術可以在質量最小的前提下，使結構的性能達到最優。目前，在工業界的應用已逐漸成熟。文中主要探討在頂蓋結構的設計過程中，如何利用結構優化技術，在兼顧輕量化設計的前提下，使頂蓋各性能滿足設計要求。

1 結構優化技術

優化設計有三要素，即設計變量、目標函數和約束條件。設計變量是發生改變從而提高性能的一組參數；目標函數要求最優的設計性能，是關于設計變量的函數；約束條件是對設計的限制，是對設計變量和其他性能的要求。優化數學模型可表述為:

Minimize:f(X)=f(x1,x2,……,xn)

Subject to:g(X)≤0j=1,……,m

hk(X)≤0k=1,……,mh

其中：X=(x1,x2,……,xn)是設計變量，如產品的結構尺寸等；f(X)是設計目標，如各種力學性能或者質量；g(X)和h(X)是需要進行約束的設計響應，如對產品工作時的變形和應力水平進行約束。

1.1 基于OptiStruct的優化方法

OptiStruct是一個面向產品設計、分析和優化的有限元和結構優化求解器，它提供拓撲優化、形貌優化、尺寸優化、形狀優化及自由尺寸和自由形狀優化，這些方法被廣泛應用于產品開發過程的各個階段。此研究涉及其中3種優化設計方法：形狀優化、形貌優化與尺寸優化。

在形貌優化中，設計空間由大量的節點波動向量組成，這些節點波動向量按照一定的模式進行組合以滿足設計約束，并最終生成優化后的最佳形貌。此優化方法適用于在鈑金件上找出最佳的加強筋位置和形狀。在形狀優化中，通過將網格節點移動到新的位置，改變零件的形狀，從而提高零部件的性能。此種優化方法常用于優化零件的位移和幾何形狀。OptiStruct形狀優化采用非參數化的優化方法,將設計空間分成若干控制區域, 每個區域的形狀簡化為關鍵控制節點位置, 通過移動這些關鍵節點, 產生邊界形狀的變化。形狀設計變量為關鍵節點的位置。在尺寸優化中，網格模型保持不變，只改變模型的參數，可以對有限元模型的各種參數，如板件厚度、材料特性等進行優化。

1.2 汽車頂蓋結構優化設計技術路線

以結構優化結果為指導，進行頂蓋結構設計。首先，對影響頂蓋各性能的因素進行分析，并將其轉變為可參數化的設計變量；其次，進行頂蓋結構初步設計，并針對不同的設計變量選擇適合的優化方法；最后，依據優化后的設計變量進行頂蓋的詳細結構設計，并校核其性能是否滿足設計要求。

影響頂蓋性能的因素可分為兩類：一類為頂蓋外板，另一類為頂蓋橫梁。頂蓋外板因素一般包括頂蓋外板曲率分布、有無筋條、筋條數量、筋條形狀等，頂蓋橫梁變量一般包括橫梁數量、橫梁位置、橫梁的形狀及厚度。頂蓋外板為雙曲率大平面，曲率是不易優化的變量，為此，將頂蓋曲率轉變為頂蓋弦高進行處理。

優化外板變量不需要增加質量，且對各性能的影響較大，因此先優化外板變量，再優化橫梁變量。由于外板變量對各性能的影響規律不一，按先確定頂蓋外板曲率分布、再確定筋條數量、最后確定筋條形狀的設計思路，進行外板變量的優化。以需要對頂蓋全部的影響因素進行優化為例，頂蓋結構的優化設計路線如圖1所示。

圖1 頂蓋結構優化設計技術路線

2 頂蓋初始結構設計

文中以某車型頂蓋結構為例，進行結構優化設計。首先進行頂蓋初始結構設計，并分析其各項性能。

2.1 初始結構設計方案

頂蓋初始結構設計在滿足總布置要求及側碰等關鍵約束要求的基礎上進行，主要遵循以下幾條原則：(1)根據造型A面設計頂蓋外板；(2)根據側碰性能要求及頂蓋安裝等總布置要求確定橫梁的數量及布置；(3)在滿足前兩項要求的前提下，按照質量最輕的輕量化原則進行頂蓋結構設計。

頂蓋結構的初始設計方案如圖2所示，頂蓋總成各零件的初始設計厚度如表1所示。

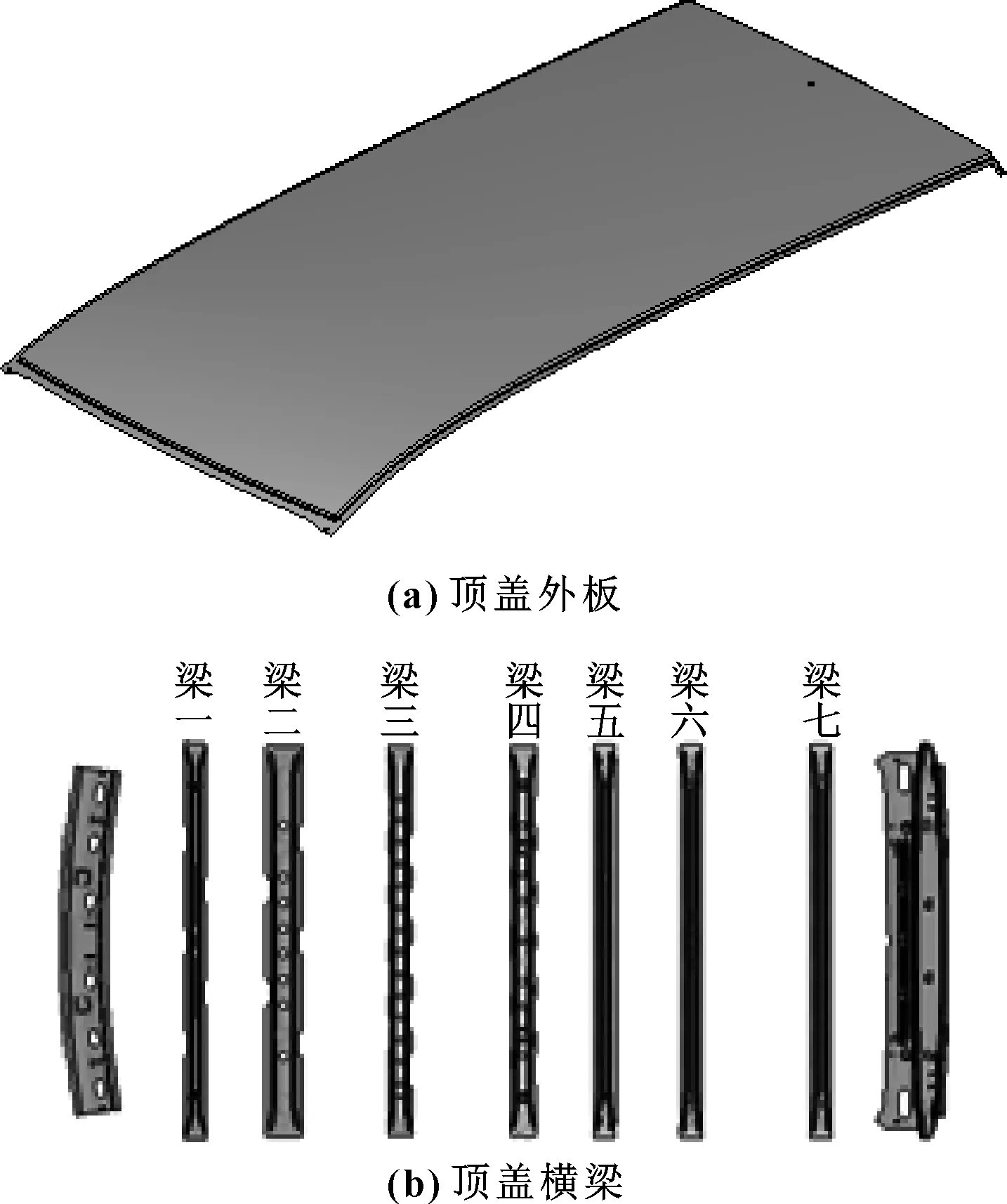
圖2 頂蓋初始結構設計方案

表1 頂蓋零件設計厚度mm

2.2 初始結構性能分析

對初始設計方案的各性能進行有限元分析。為模擬頂蓋的邊界條件，分析模型截取一部分的白車身結構，并在階段處約束全部自由度，頂蓋結構性能分析有限元模型如圖3所示，各性能指標及分析方法如表2所示。

圖3 頂蓋結構性能分析模型

分析項初始設計結構分析值目標值分析方法質量/kg22.4323———模態/Hz47.8945模態分析,一階模態抗凹初始剛度/(N·mm-1)17(最弱處)>20非線性分析,初始剛度抗雪壓/cm33>70屈曲分析,一階屈曲因子

從初始結構的性能分析結果來看，除了模態結果達標外，其他的性能均不達標，需要進行優化設計。

3 頂蓋結構優化設計

根據總布置、造型及質量等要求，在初始結構的基礎上，可優化的設計變量為頂蓋弦高、加4～6根筋條、筋條形狀，及優化橫梁五、橫梁六、橫梁七的截面尺寸。設計變量的取值范圍及優化方法如表3所示。

表3 某車型頂蓋設計變量、取值范圍及優化方法

3.1 頂蓋弦高優化

選擇頂蓋外板的弦高作為形狀設計變量，使用HyperMorph創建包含頂蓋外板和橫梁的控制塊，合理劃分控制塊，將模型分成多個域。通過移動控制塊的控制柄使頂蓋的弦高發生變化。設置優化問題描述如下：(1)設計變量為頂蓋最高點處的控制柄位置，取值范圍：Z正向移動0～17 mm；(2)設計約束為一階模態頻率大于45 Hz；(3)設計目標為一階屈曲因子最大。

運行OptiStruct 軟件對頂蓋的弦高進行優化計算，優化結果如圖4(a) 所示，當設計變量取最大值時，一階模態大于45 Hz，一階屈曲因子最大。根據優化結果，將頂蓋弦高提高17 mm，優化后的頂蓋外板如圖4(b)所示。對優化后結構進行性能校核，一階模態61.02 Hz；一階屈曲因子0.86(對應抗雪壓厚度60 cm)；抗凹性能最弱點初始剛度17.5 N/mm。

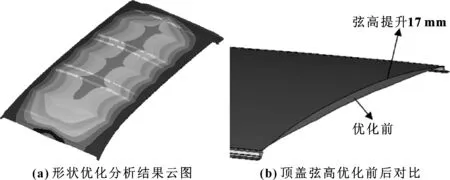
圖4 頂蓋弦高優化——形狀優化

頂蓋弦高優化后，模態滿足要求，抗雪壓厚度由33 cm提升至60 cm，抗凹初始剛度提升不大。抗雪壓性與抗凹性仍不滿足目標值的要求，需進一步優化。

3.2 筋條數量優化

設置頂蓋橫梁二與頂蓋后橫梁間的頂蓋外板區域為優化區域，優化區域X向長度1 680 mm。起筋的參數定義：起筋的最小寬度67 mm，起筋角度60°，起筋高度5 mm。沿X向設置線性起筋約束，設置優化問題描述如下：(1)設計變量為優化區域內節點相對殼單元中性面法向的擾動；(2)設計約束為一階模態頻率大于42 Hz，一階屈曲因子大于1；(3)設計目標為在頂蓋大面上施加均布力對應的工況柔度最小。

運行OptiStruct 軟件對后地板加強筋布局進行優化計算，頂蓋外板起筋形式如圖5(a)所示。根據分析結果，在頂蓋外板上起4根長1 680 mm、寬77 mm、高5 mm的筋條，結構如圖5(b)所示。對優化后結構進行性能校核：一階模態42 Hz，一階屈曲因子1.2(對應抗雪壓厚度84 cm)，抗凹初始剛度21.5 N/mm。

圖5 筋條數量優化——形貌優化

增加筋條后，雖然抗雪壓性能與抗凹性能滿足要求，但模態由61.02 Hz下降至42 Hz，需進一步優化筋條的形狀。

3.3 筋條形狀優化

根據造型區域設計，選擇筋條長度作為形狀設計變量，使用HyperMorph在筋條末端(即靠近車尾端)創建域和控制柄。通過移動控制柄使筋條的長度發生變化。設置優化問題描述如下：(1)設計變量為筋條末端的控制柄位置，取值范圍：X正向移動0～300 mm；(2)設計約束為一階屈曲因子大于0.9；(3)設計目標為模態最大。

運行OptiStruct 軟件對筋條的長度進行優化計算，優化結果如圖6(a) 所示，筋條長度縮短290 mm。結合造型區域的要求，優化后的筋條如圖6(b)所示。對優化后結構進行性能校核：一階模態45.3 Hz，一階屈曲因子0.9(對應抗雪壓厚度63 cm)，抗凹初始剛度20.4 N/mm。

圖6 筋條形狀優化

筋條的長度從尾端起縮短290 mm后，模態提升的同時，抗雪壓性能下降，抗凹初始剛度變化不大。從分析結果看，模態與抗雪壓性能雖然都不滿足設計目標，但離目標值很近，需進一步優化頂蓋橫梁的設計變量。

3.4 橫梁形狀優化

選擇橫梁五、橫梁六、橫梁七的寬和高作為形狀設計變量，使用HyperMorph創建橫梁寬度尺寸和高度尺寸的域和控制柄。通過移動控制柄使橫梁的截面形狀發生變化。設置優化問題描述如下：(1)設計變量為橫梁截面的控制柄位置，取值范圍：X正負向移動0～15 mm；Z負向移動0～5 mm；(2)設計約束為一階模態大于45 Hz、一階屈曲因子大于1；(3)設計目標為質量最小。

運行OptiStruct 軟件對橫梁的截面形狀進行優化計算，優化結果如圖7(a) 所示，當橫梁的Z向尺寸沿負Z向增加10 mm，橫梁五、六、七的X向尺寸以梁中心位置擴寬5 mm，一階模態大于45 Hz，一階屈曲因子大于1。根據優化結果，以寬27 mm、高27 mm設計橫梁五、六、七截面，優化后的截面尺寸如圖7(b)所示。對優化后結構進行性能校核：一階模態46.2 Hz；一階屈曲因子1.3(對應抗雪壓厚度91 cm)；抗凹初始剛度20.4 N/mm。由于截面變大，質量增加0.35 kg。

圖7 橫梁形狀優化

橫梁截面形狀優化后，頂蓋的各項性能均滿足設計目標要求，不需要再進行優化。

3.5 頂蓋結構優化設計

經過以上結構優化，頂蓋的各項性能指標已滿足設計目標要求。根據優化過程中各設計變量的最優值進行頂蓋結構設計，最終的頂蓋結構如圖8所示。

圖8 頂蓋優化設計結構

由優化過程可知：在頂蓋初始結構的基礎上，經過優化設計，僅增重0.355 kg，即使頂蓋各項性能滿足設計目標要求。增重后，頂蓋質量為22.785 kg，比目標值低，滿足輕量化的設計要求。

4 結論

(1)基于結構優化技術的頂蓋設計方法，在滿足總布置要求及側碰等關鍵約束要求的基礎上，以質量最輕為原則進行頂蓋初始結構設計，在優化過程中優先優化不增重的設計變量，保證了頂蓋結構的輕量化設計；

(2)在運用結構優化技術對設計變量進行優化的過程中，通過合理選擇優化方法、設置優化目標和約束，在變量的取值范圍內找到最優化值，為設計出滿足頂蓋模態、抗雪壓及抗凹性的頂蓋結構提供了指導，避免了設計反復。